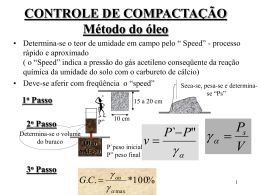
COMPACTAÇÃO DOS SOLOS
1
Introdução
Compactação: processo manual ou mecânico que visa reduzir o volume de vazios do solo,
melhorando as suas características de resistência, deformabilidade e permeabilidade.
Objetivo: Melhoria e Estabilidade de propriedades mecânicas dos solos:




Redução da compressibilidade;
Aumento da resistência;
Aumento da capacidade de carga das bases e sub-bases dos pavimentos;
Redução da permeabilidade.
Emprego:





Construção de aterros;
Construção de camadas constitutivas de pavimentos
Construção de barragens de terra;
Preenchimento com solo entre maciço e estrutura de arrimo;
Reenchimento de cavas de fundações e de tubulações enterradas.
Técnica básica:
 Lançamento de material de empréstimo (oriundo de jazida) ou do próprio local
(reenchimentos);
 Passagem de equipamentos que transmitam ao solo a energia de compactação ⇒
carga móvel (amassamento, impacto ou vibração) ou estática.
Compactação x Adensamento
74
2
Ensaio de Compactação
Determinação experimental da correlação entre γ d e w para uma dada energia de
compactação → Curva de Compactação.
Idealizado por R. Proctor (1933) → Ensaio Proctor Normal → NBR 7128/86 – Ensaio Normal
de Compactação.
A seguir são listadas, de modo resumido, as principais fases de execução de um ensaio de
compactação.
 Ao se receber uma amostra de solo (no caso, deformada) para a realização de um
ensaio de compactação, o primeiro passo é colocá-la em bandejas de modo que a
mesma adquira a umidade higroscópica (secagem ao ar). O solo então é destorroado
e passado na peneira #4, após o que se adiciona água na amostra para a obtenção do
primeiro ponto da curva de compactação do solo.
 Após preparada a amostra de solo, a mesma é colocada em um recipiente cilíndrico
com volume igual a 1000 ml e compactada com um soquete de 2500 g, caindo de
uma altura de aproximadamente 30cm, em três camadas com 25 golpes do soquete
por camada, como demonstra a Figura 20.
 Este processo é repetido para amostras de solo com diferentes valores de umidade,
utilizando-se em média cinco pontos para a obtenção da curva de compactação.
 De cada corpo de prova assim obtido, determinam-se o peso específico do solo seco
e o teor de umidade de compactação.
 Depois de efetuados os cálculos dos pesos específicos secos e das umidades, lançamse esses valores ( γ d , w ) em um par de eixos cartesianos, tendo nas ordenadas os
pesos específicos do solo seco ( γ d ) e nas abscissas os teores de umidade
( w) ,
como mostra a Figura 21.
Figura 20 – Ensaio de Compactação (Proctor Normal)
Figura 21 – Curva de Compactação
75
Típica
Com cinco ou seis pares de valores ( γ d , w ) obtidos constrói-se por ajuste manual aos
pontos, a curva de compactação e desta estima-se os valores de γ d max e wot .
Ajuste → retas definindo os ramos seco e úmido e uma parábola fazendo a transição entre
as duas.
É geralmente representada em conjunto com a curva de saturação do solo e opcionalmente
curvas de igual grau de saturação (Figura 22). Como no processo de compactação não
conseguimos nunca expulsar todo o ar existente nos vazios do solo, todas as curvas de
compactação (mesmo que para diferentes energias) se situam à esquerda da curva de
saturação. A curva de saturação do solo pode ser representada pela equação (1).
γd =
γ w ⋅ S ⋅γ S
w⋅γ S + γ w ⋅ S
(1)
Figura 22 – Curvas de Saturação.
2.1
Curva de Compactação
A Figura 23 mostra uma curva de compactação obtida através do ensaio de compactação
com uma mesma energia de compactação.
Figura 23 – Curva de Compactação
Umidade ótima → teor de umidade para o qual se obtém o maior valor de γ d ( γ d max ) .
76
Ramo seco → ramo da curva de compactação anterior ao valor de umidade ótima. → a
umidade é baixa, a água contida nos vazios do solo está sob o efeito capilar e exerce uma
função aglutinadora entre as partículas.
À medida que se adiciona água ao solo ocorre a destruição dos benefícios da capilaridade,
tornando-se mais fácil o rearranjo estrutural das partículas.
Ramo úmido → ramo da curva de compactação posterior ao valor de umidade ótima → a
umidade é elevada e a água se encontra livre na estrutura do solo, absorvendo grande parte
da energia de compactação.
Baixo teor de umidade → o atrito entre partículas é alto dificultando a
compactação.
Aumento no teor de umidade → efeito de lubrificação entre as partículas,
aumentando a compactação enquanto a saída de ar é facilitada.
Após certo teor de umidade próximo a saturação → umidade ótima wot → a
compactação não consegue mais expulsar o ar dos vazios, a maior quantidade de
água resulta em redução de densidade.
2.2
Energia de Compactação
Mantendo-se o procedimento de ensaio descrito no item 2, um ensaio de compactação
poderá ser realizado utilizando-se diferentes energias. A energia de compactação ( J m3 ) 4
empregada em um ensaio de laboratório pode ser facilmente calculada mediante o uso da
equação (2).
E=
P⋅h⋅ N ⋅n
V
(2)
Onde V é o volume de solo compactado ( m3 ) , n é o número de camadas, N é o número
de golpes por camada, h a altura de queda do soquete ( m ) e P é o peso do soquete ( N ) .
No campo → energia de compactação é proveniente do número de passadas do rolo
compactador em uma camada de solo.
No laboratório → por impacto, esmagamento ou compressão estática.
4
1J= N ⋅ m
77
2.3
Influência da Energia de Compactação
À medida que se aumenta a energia de compactação, há uma
redução do teor de umidade ótimo e uma elevação do valor do peso
específico seco máximo. A Figura 4 apresenta curvas de compactação
obtidas para diferentes energias.
E
wot
γ d max
Figura 24 – Efeito da Energia de Compactação nas Curvas de Compactação
Com o surgimento de novos equipamentos de campo, de grande porte, com possibilidade
de elevar a energia de compactação e capazes de implementar uma maior velocidade na
construção de aterros, houve a necessidade de se criar em laboratório ensaios com maiores
energias que a do Proctor Normal. A Tabela 10 apresenta-se uma comparação entre os
padrões adotados para a realização dos ensaios de compactação por diferentes órgãos.
Tabela 10 – Comparação entre alguns padrões adotados para o ensaio de compactação.
78
2.4
Influência da Compactação na Estrutura dos Solos
Figura 25 – Influência da compactação na
estrutura dos solos.
Ramo seco (baixa umidade) → a atração
face-aresta das partículas não é vencida
pela energia de compactação → estrutura
floculada.
Ramo úmido (próximo a saturação) → a
repulsão entre partículas aumenta e a
compactação orienta as partículas →
estrutura dispersa.
Para uma mesma umidade → maior a
dispersão quanto maior a energia de
compactação.
Redução de Permeabilidade → ensaios realizados acima da umidade ótima (geralmente
algo em torno de 2%). Isto é feito de forma a se gerar uma estrutura dispersa do solo, com
grãos orientados na direção perpendicular ao esforço de compactação empregado
2.5
Influência do Tipo de Solo na Curva de Compactação
Solos grossos → os solos grossos tendem
a exibir uma curva de compactação com
um maior valor de γ d max e um menor
valor de wot do que solos contendo
grande quantidade de finos (Figura 26).
Solos finos → as curvas de compactação
Figura 26 – Influência do tipo de solo na curva de são bem mais "abertas" do que aquelas
compactação.
obtidas para solos grossos (Figura 26).
2.6
Curva de Resistência ou Estabilidade
Curvas que mostram a resistência oferecida pelo solo compactado à penetração de um
pistão metálico de peso e área de seção padronizados → agulha de Proctor – em função da
umidade de compactação.
79
 Quanto maior a umidade
menor a resistência do solo.
PORQUE OS SOLOS NÃO SÃO
COMPACTADOS EM CAMPO EM
VALORES DE UMIDADE INFERIORES
AO VALOR ÓTIMO?
Figura 27 – Variação da resistência dos solos com o teor
de umidade de compactação. Modificado de Caputo
(1981).
Observa-se que na wot não se tem a maior resistência, entretanto tem-se maior
estabilidade → menor redução de resistência com o aumento do teor de umidade pelas
chuvas.
Princípio fundamental na compactação → busca-se obter a densidade máxima, que não
implica numa resistência máxima, mas sim maior estabilidade sob adversidades climáticas.
3
Compactação no Campo
A compactação no campo consiste das seguintes operações:
a) Escolha da área de empréstimo: problema técnico-econômico →distância de
transporte, características geotécnicas e umidade do material em relação à umidade
de compactação.
b) Limpeza e regularização da área de trabalho.
c) Lançamento e espalhamento do material → uso de motoscrapers ou unidades de
transporte.
d) Regularização da camada → uso de motoniveladora para acerto da altura da
camada.
Espessura das camadas→ ≤ 30 cm de material fofo para se ter 15 a 20 cm de
espessura de solo compactado (incluindo 2 a 5 cm da camada anterior).
80
e) Pulverização e homogeneização do material da camada → remoção ou
desagregação de torrões secos, material aglomerado ou fragmentos de rocha
alterada por uso de escarificadores ou arados de disco.
f) Acerto da umidade → irrigação (caminhões pipa e irrigadeiras) ou aeração (arados
de disco). Homogeneização e conferência da umidade.
g) Compactação propriamente dita→ uso de equipamentos escolhidos de acordo com
o tipo de solo e serviço.
h) Controle de compactação → controle sobre os valores de γ d max e wot pelo grau de
compactação especificado.
i) Escarificação para a camada seguinte.
3.1
Equipamentos de Campo
Os valores de peso específico seco máximo obtidos são fundamentalmente função de
 Tipo do solo;
 Quantidade de água utilizada;
 Energia específica aplicada pelo equipamento que será utilizado → função do tipo e
peso do equipamento, espessura da camada de compactação e do número de
passadas sucessivas aplicadas.
Os processos de compactação de campo geralmente combinam a vibração com a pressão, já
que a vibração utilizada isoladamente se mostra pouco eficiente, sendo a pressão necessária
para diminuir, com maior eficácia, o volume de vazios interpartículas do solo.
Os equipamentos de compactação são divididos em três categorias:
 Soquetes → Manuais ou Mecânicos (IMPACTO)
 Rolos Estáticos → Dentados, Lisos e Pneumáticos (PISOTEAMENTO)
 Rolos Vibratórios (VIBRAÇÃO)
3.1.1 Soquetes
 Compactadores de impacto utilizados em
locais de difícil acesso para os rolos
compressores, como em valas, trincheiras,
etc.
 Podem ser manuais ou mecânicos (sapos).
 A camada compactada deve ter 10 a 15cm
para o caso dos solos finos e em torno de
15cm para o caso dos solos grossos (Figura
28).
Figura 28 – Compactadores manuais
81
3.1.2 Rolos Estáticos
a) Pé-de-Carneiro
 Tambor metálico com protuberâncias (patas) solidarizadas, em forma troncocônica e
com altura de aproximadamente de 20cm;
 Indicado na compactação de solos coesivos;
 Promove um grande entrosamento entre as camadas compactadas;
 A camada compactada possui espessura variando de 15 a 20 cm, com número de
passadas variando entre 4 e 6 para solos finos e de 6 a 8 para os solos grossos.
A Figura 29 mostra um rolo compactador do tipo pé-de-carneiro. A Figura 30 ilustra o
aspecto da superfície de solo compactado após o uso do pé-de-carneiro.
Figura 29 – Equipamento do tipo rolo pé-decarneiro.
Figura 30 – Aspecto da superfície de solo após o
uso do rolo pé-de-carneiro.
b) Rolo Liso
 Cilindro oco de aço, podendo ser
preenchido
por
areia
úmida,
pedregulho ou água, a fim de que seja
aumentada a pressão aplicada.
 Usados em bases de estradas, em
capeamentos e são indicados para
solos arenosos, pedregulhos e pedra
Figura 31 – Rolo liso.
britada, lançados em espessuras
inferiores a 15cm.
 Este tipo de rolo compacta bem camadas finas de 5 a 15cm com 4 a 5 passadas. Os
rolos lisos possuem pesos de 1 a 20t e freqüentemente são utilizados para o
acabamento superficial das camadas compactadas.
 Para a compactação de solos finos utilizam-se rolos com três rodas com pesos em
torno de 10t, para materiais de baixa plasticidade e 7t, para materiais de alta
plasticidade.
82
A Figura 31 ilustra rolos compactadores do tipo liso. Os rolos lisos possuem certas
desvantagens como:
− Pequena área de contato.
− Em solos de pequena capacidade de suporte afundam demasiadamente dificultando
a tração.
− Necessidade de melhoria do entrosamento entre camadas por escarificação.
c) Rolo Pneumático
 Eficientes na compactação
de capas asfálticas, bases
e sub-bases de estradas e
indicados para solos de
granulação fina a arenosa.
Não deve ser utilizado na
compactação de areia de
Figura 32 – Rolo Pneumático.
granulometria uniforme.
 Os rolos pneumáticos podem ser utilizados em camadas mais espessas e possuem
área de contato variável, função da pressão nos pneus e do peso do equipamento.
 Podem-se usar rolos com cargas elevadas obtendo-se bons resultados. Nestes casos,
muito cuidado deve ser tomado no sentido de se evitar a ruptura do solo.
3.1.3 Rolos Vibratórios
 A freqüência da vibração influi
de maneira extraordinária no
processo de compactação do
solo.
 São utilizados eficientemente
na compactação de solos
granulares (areias), onde os
rolos pneumáticos ou pé-decarneiro não atuam com
eficiência.
Figura 33 – Rolo Vibratório.
Os rolos vibratórios possuem as seguintes desvantagens:
 Não compactam bem próximo à superfície, o que requer acabamento com rolo liso
ou pneumático;
83
 Podem produzir uma segregação vertical quando há excesso de finos: as partículas
graúdas descem; este defeito é pouco acentuado com solos de boa granulometria
3.1.4 Escolha dos Equipamentos de Compactação
Equipamento
Solos Coesivos
Rolos Lisos
Rolos de Pneus
Rolos Pé-de-carneiro
Rolos Vibratórios
Adequado
Adequado
Adequado
Inadequado
3.2
Granulometria
Contínua
Adequado
Adequado
Inadequado
Adequado
Solos Não Coesivos
Granulometria
Uniforme
Aceitável
Aceitável
Inadequado
Aceitável
Materiais
Pedregulhosos
Adequado
Aceitável
Inadequado
Adequado
Controle da Compactação
Cuidados a serem tomados:
 A espessura da camada lançada não deve exceder a 30 cm, sendo que a espessura
da camada compactada deverá ser menor que 20 cm.
 Deve-se realizar a manutenção da umidade do solo o mais próximo possível da
umidade ótima.
 Deve-se garantir a homogeneização do solo a ser lançado, tanto no que se refere à
umidade quanto ao material.
84
3.2.1 Procedimentos Usuais de Controle da Compactação:
 Coletam-se amostras de solo da área de empréstimo e efetua-se em laboratório o
ensaio de compactação. Obtêm-se a curva de compactação e daí os valores de peso
específico seco máximo e o teor de umidade ótimo do solo.
 No campo, à proporção em que o aterro for sendo executado, deve-se verificar, para
cada camada compactada, qual o teor de umidade empregado e compará-lo com a
umidade ótima determinada em laboratório. Este valor deve atender a seguinte
especificação:
wcampo − 2% < wot < wcampo + 2%
 Nas figuras abaixo (Figura 34 e Figura 35) são apresentadas fotos ilustrativas de
processos de aeração (para redução da umidade) e umedecimento (para aumento
da) da camada de solo a ser compactada, respectivamente. É importante frisar que o
solo a ser compactado deve passar, preferencialmente, por uma etapa de repouso
para equalização de umidade, de pelo menos um dia. No momento da compactação
o valor de umidade do solo deve sofrer somente alguns ajustes.
 Determina-se também o peso específico seco do solo no campo, comparando-o com
o obtido no laboratório. Define-se então o grau de compactação do solo, dado pela
razão entre os pesos específicos secos de campo e de laboratório.
=
GC
γd
campo
γd
⋅100%
max
 Deve-se obter sempre valores de grau de compactação superiores a 95%.
 Caso estas especificações não sejam atendidas, o solo terá de ser revolvido, e uma
nova compactação deverá ser efetuada.
Figura 34 – Processo de aeração.
Figura 35 – Processo de umedecimento
85
3.2.2 Determinação do Teor de Umidade no Campo
a) Método de Speedy (Speedy Moisture Test)
Umidímetro "Speedy"  recipiente metálico, hermeticamente fechado, onde são colocadas
duas esferas de aço, a amostra do solo da qual se quer determinar a umidade e uma ampola
de carbureto – carbonato de cálcio (CaC2).
Determinação da umidade  agita-se o frasco, a
ampola é quebrada pelas esferas de aço e o CaC2
combina-se com a água contida no solo, formando o
gás acetileno, que exercerá pressão no interior do
recipiente, acionando o manômetro localizado na
tampa do aparelho.
Com o valor de pressão medido, os valores de
umidade são obtidos através de uma tabela
específica, que correlaciona a umidade em função da
pressão manométrica e do peso da amostra de solo.
Figura 36 – Equipamento “Speedy”
b) Método da Frigideira;
c) Uso do equipamento de micro-ondas;
d) Nuclear Moisture Density Meter  baseado na emissão de raios gama e nêutrons, a
reflexão destes elementos está relacionada com a densidade e umidade,
respectivamente.
3.2.3 Determinação do Peso Específico
a) Método do Frasco de Areia
Faz-se uma cavidade na camada do solo compactado, extraindo-se o solo e pesando-o em
seguida. Para se medir o volume da cavidade, coloca-se o frasco de areia com a parte do
funil para baixo sobre a mesma e abre-se a torneira do frasco, deixando-se que a areia
contida no frasco encha a cavidade por completo. O volume de areia que saiu do frasco é
igual ao volume de solo escavado, de modo que o peso específico do solo pode ser
determinado.
b) Método do cilindro cortante
A Figura 37 apresenta uma seqüência de passos adotados na cravação de um cilindro rígido
em uma camada de solo compactada. Após a cravação, o solo é rasado e o peso do cilindro
mais o solo é determinado.
86
Figura 37 – Fotos ilustrativas de passos para a cravação de um cilindro de parede rígida em uma
camada de solo compactada.
Freqüência do controle (especificações de terraplanagem do DNER):
 1 ensaio de compactação para cada 1000 m3 de material compactado;
 1 controle de densidade para cada 1000 m3 de material compactado;
 Para camadas finas  1 controle de densidade para cada 100 m de extensão,
alternativamente no centro e nas bordas.
Outros métodos de controle de compactação (Descritos em: Introdução a Mecânica dos
Solos – Milton Vargas – cap.2):
 Método de Hilf;
 Método das famílias de curvas de compactação
 Relações empíricas estabelecidas com base em estudos estatísticos
3.2.4 Influência do Número de Passadas do Rolo
Com o progresso da compactação em campo, o número de passadas do rolo vai perdendo a
sua eficiência na compactação do solo. Deste modo, a compactação dos solos em campo é
definida para um determinado número de passadas, normalmente inferior a 10.
Este número dependerá do tipo de solo a ser compactado, do tipo de equipamento
disponível, e das condições particulares de cada caso.
Grandes obras  aterros experimentais para se determinar o número ótimo de passadas do
rolo.
Em geral, 8 a 12 passadas do rolo em uma camada de solo a ser compactada é suficiente.
Caso com 15 passadas não se atinja o valor do peso específico seco determinado, é
recomendável que se modifique as condições antes fixadas para a compactação.
87
Exercícios
1 – Com uma amostra de solo argiloso, com areia fina, a ser usado num aterro, foi feito um
Ensaio Normal de Compactação (Ensaio Proctor). Na tabela abaixo estão as massas dos
corpos de prova, determinadas nas cinco moldagens de corpo de prova, no cilindro que
tinha 99s cm3. Estão também indicadas as umidades correspondentes a cada moldagem. A
densidade relativa dos grãos é 2,65.
a) Desenhar a curva de compactação e determinar a densidade máxima e a umidade
ótima.
b) Determinar o grau de saturação do ponto máximo da curva.
c) Representar a Curva de Saturação e a Curva de igual valor de saturação que passa
pelo ponto máximo da curva.
Número do Ensaio
Massa do corpo de prova (kg)
Umidade do solo compactado (%)
1
1,748
17,73
2
1,817
19,79
3
1,874
21,59
4
1,896
23,63
5
1,874
25,75
2 – Foi especificado que o aterro do exercício anterior deve ser compactado com Grau de
Compactação de pelo menos 95% e com umidade no intervalo wot − 2 < wot < wot + 1 . Em
que umidade pode o solo estar na ocasião da compactação e a que densidade ele deve ser
compactado?
3 – Com o mesmo solo, foi feito um ensaio Proctor Modificado, em que o solo foi
compactado em um cilindro com 2,085 dm3 de volume, com o soquete de massa de 4,536
kg e altura de queda de 45,7 cm, aplicando-se 55 golpes por camada em cinco camadas.
Neste ensaio determinou-se um peso específico seco de 16,57 kN/m3. Estime a umidade
ótima que este solo deve apresentar.
4 – Considere um lote de terreno retangular, medindo horizontalmente 12 m de frente por
42 m de frente a fundo, situado em uma encosta com declividade uniforme e constante ao
longo da sua extensão, cujas curvas de nível são, portanto, paralelas aos lados de menor
dimensão, com a frente na cota de 28 m e o fundo na cota de 22 m.
Para realização de um projeto de engenharia, foi inicialmente transformada a topografia
deste terreno em uma plataforma horizontal nivelada na cota de 24,60 m, através de uma
operação de corte vertical e aterro, bem como da construção de um muro de arrimo
circundante ao longo de todo o perímetro, de modo a assegurar a sustentação da zona de
corte e a verticalidade do aterro.
88
O aterro foi executado de modo a garantir
um grau de compactação igual a 100% do
peso específico máximo obtido através de
ensaios normais de Proctor, cujos resultados
são apresentados na Curva de Compactação
da figura ao lado.
Por outro lado, na zona de corte, a superfície
da plataforma foi escarificada até a
profundidade de 20 cm e recompactada nas
mesmas condições do aterro, de modo a se
obter uniformidade ao longo de toda a
superfície.
Com base nestes dados e nas informações prestadas a seguir, determine:
a) o volume de solo no seu estado natural de campo que foi necessário acrescentar, através
de empréstimo, ou descartar, através de bota-fora, para compensar os volumes destas
operações de escavação e aterro, desprezando nos cálculos a espessura do muro de arrimo
circundante;
b) o volume de água por metro cúbico de solo, no seu estado natural de campo, necessário
para corrigir o teor de umidade natural de modo a obter a condição especificada de
compactação.
Dados/Informações Adicionais
Peso específico do solo (na umidade do campo) = 16,40 kN/m3 e teor de umidade natural
do solo no campo = 13,5 %
Equation Chapter (Next) Section 1
89
TENSÕES NOS SOLOS
Como em todo material utilizado na engenharia, o solo, ao sofrer solicitações, irá se
deformar, modificando o seu volume e forma iniciais. A magnitude das deformações
apresentadas pelo solo irá depender não só de suas propriedades intrínsecas de
deformabilidade (elásticas e plásticas), mas também do valor do carregamento a ele
imposto.
Esforços nos Solos
• Peso próprio do solo sobrejacente (estado de tensões inicial)
• Cargas externas aplicadas ao solo  construções (estado de tensões finais)
1
Conceito de Tensões num Meio Particulado
Aplicação da Mecânica dos Sólidos Deformáveis aos solos  conceito de tensões num meio
particulado  os solos são constituídos por partículas e as forças são transmitidas de
partícula a partícula e suportadas, também pela água dos vazios.
Transmissão de esforços entre partículas
− Partículas granulares → transmissão de forças através
do contato direto grão a grão.
− Partículas de argila → pode ocorrer através da água
adsorvida.
A transmissão se dá por áreas muito reduzidas. Ao longo de
um plano horizontal no solo têm-se esforços decompostos em
componentes normais e tangenciais.
2
Tensões Geostáticas (devidas ao peso próprio)
Situação de Tensões Geostáticas
• Nível do terreno é horizontal;
• Natureza do solo não varia horizontalmente;
• Não há carregamento externo próximo a região considerada.
90
Figura 38 – Perfil geotécnico e tensões atuantes em um elemento de solo.
Em uma situação de tensões geostáticas, portanto, a tensão normal vertical inicial (σ V ) no
ponto “A” pode ser obtida considerando o peso do solo acima do ponto “A” dividido pela
área.
σV =
W γ ⋅ b2 ⋅ z
=
= γ ⋅z
A
b2
(1)
Onde W = γ ⋅ V é o peso do prisma ( kN ) , V= b 2 ⋅ z é o volume do prisma ( m3 ) , A = b 2 é a
área do prisma ( m 2 ) e γ é o peso específico natural do solo ( kN / m3 ) .
Se o solo acima do ponto “A” for estratificado, isto é, composto de “n” camadas, o valor de
(σ V )
é dado pelo somatório de γ i , zi , onde i varia de 1 a n .
=
σV
n
∑γ
i =1
i
⋅ zi
(2)
Exemplo: Para o perfil indicado abaixo, determine a tensão total no ponto A e no ponto B.
3m
A
γ = 18 kN / m3
Solução :
σ V = γ ⋅ z = 18 ⋅ 3 = 54 kPa
A
4m
B
γ = 20 kN / m3
σV =
B
∑γ
i
⋅ z i = 18 ⋅ 3 + 20 ⋅ 4 = 134 kPa
91
3
Pressões Neutras e Princípio das Tensões Efetivas
Pressão Neutra ou Poropressão ( u )
• Toda pressão que atua na água intersticial dos solos, seja ela gravitacional
ou capilar;
• Independe da porosidade do solo;
• Depende somente da sua profundidade em relação ao nível freático.
u γw ⋅z
=
(3)
Tensão Efetiva (σ ′ )
• Tensão que atua no contato entre partículas;
• Controla toda a deformação e resistência da estrutura sólida do solo.
3.1
Princípio das Tensões Efetivas
Ao notar a natureza das forças atuantes, Terzaghi identificou que a Tensão Normal Total
num plano qualquer deve ser considerada como a soma de duas parcelas: a tensão efetiva e
a poropressão.
Princípio das Tensões Efetivas
• A tensão efetiva, para solos saturados, pode ser expressa por:
σ =′ σ − u
(4)
• Todos os efeitos mensuráveis resultantes de variações de tensões nos solos,
como compressão, distorção e resistência ao cisalhamento, são devidos a
variações de tensões efetivas.
Onde σ ′ é a tensão efetiva do solo ( kPa ) , σ é a tensão total ( kPa ) e u é a pressão
neutra (poro-pressão) ( kPa ) .
Tensões normais  suportadas, parte pelas partículas sólidas e parte pela água.
Tensões cisalhantes  somente poderão ser suportadas pelas partículas sólidas.
Devido a sua natureza de fluido, a pressão na fase água do solo não contribui para a sua
resistência, sendo assim chamada de pressão neutra. Para visualizar um pouco melhor o
92
efeito da água no solo imagine uma esponja colocada dentro de um recipiente com água
suficiente para encobri-la (a esponja se encontra totalmente submersa). Se o nível de água
for elevado no recipiente, a pressão total sobre a esponja aumenta, mas a esponja não se
deforma. Isto ocorre porque os acréscimos de tensão total são contrabalançados por iguais
acréscimos na tensão neutra, de modo que a tensão efetiva permanece inalterada (Figura
39).
(a) Esponja em repouso
(b) Peso aplicado
(c) Elevação da água
Figura 39 – Simulação para entendimento do conceito de tensão efetiva.
3.2
Cálculo da Tensão Efetiva
3.3
Exemplos
1 - Em relação ao perfil de solo da figura abaixo determinar:
a) A distribuição com a profundidade da tensão vertical total, a distribuição com a
profundidade da poropressão, a distribuição com a profundidade da tensão vertical
efetiva.
b) O valor da tensão horizontal efetiva e da tensão horizontal total na profundidade z =
12 m.
Considerar a camada superficial de argila arenosa completamente saturada devido ao
fenômeno de capilaridade.
93
2 - Traçar os gráficos de distribuição com a profundidade da tensão vertical total, da tensão
vertical efetiva e da poropressão, considerando o perfil de solo abaixo:
a) Nas condições atuais, admitindo-se capilaridade na camada de argila orgânica mole.
b) Após um rebaixamento permanente do nível d'água para a profundidade z = 2m,
seguido da remoção da camada de argila orgânica e posterior colocação de um
aterro (grande extensão) de 3m de altura com Peso específico γ = 20, 6 kN / m3 .
3 - Calcular as tensões verticais totais e efetivas nos pontos A e D do perfil geotécnico
abaixo
94
4
Acréscimos de Tensões Devido à Sobrecarga
4.1
Propagação e Distribuição de Tensões no Solo
Além do peso próprio da massa de solo, as tensões no solo podem ser originadas por
carregamentos externos.
A determinação das tensões devido a cargas externas e sua distribuição no subsolo é muito
importante na avaliação de deformações e da capacidade de carga dos terrenos onde são
instaladas obras de engenharia.
4.1.1 Distribuição das Tensões
•
•
•
Os acréscimos de tensões em uma determinada profundidade excedem a área de
projeção da área carregada;
O somatório dos acréscimos de tensões verticais, nos planos horizontais, em
qualquer profundidade, é sempre;
Os acréscimos das tensões imediatamente abaixo da área carregada diminuem é
medida que a profundidade aumenta, porque a área atingida aumenta com a
profundidade.
Figura 40 – Distribuição de tensões com a profundidade.
4.1.2 Aplicação da Teoria da Elasticidade
Para a estimativa das tensões atuantes no interior da massa de solo em virtude de
diferentes tipos de carregamento externo são muito utilizadas soluções baseadas na Teoria
da Elasticidade  relação tensão-deformação do solo é dada pela Lei de Hooke (material de
comportamento linear elástico, homogêneo e isotrópico).
Considerações Sobre Hipóteses da Teoria da Elasticidade
A aplicação de soluções mais simples da Teoria da Elasticidade aos solos é questionável, pois
os mesmos não satisfazem os requisitos das hipóteses:
− Comportamento linear (relação tensão-deformação linear) e elástico (deformações
reversíveis)  para que seja válida os acréscimos de tensão devem ser pequenos
(pequenas deformações) tal que o estado de tensões seja muito distante da ruptura.
95
− Homogeneidade (mesmas propriedades em todos os pontos)  foge a realidade na
maioria dos casos. O solo é heterogêneo pela sua natureza e também apresenta
relações tensão-deformação variáveis com a tensão de confinamento, logo variável
com a profundidade.
− Isotropia  o solo é em muitos casos anisotrópico pela natureza e arranjo de suas
partículas. Entretanto, a condição de isotropia é válida em terrenos onde o solo
mantém constituição uniforme por distâncias da ordem de algumas vezes a menor
dimensão da área carregada.
4.2
Tipos de Carregamentos e Fórmula para Cálculo do Acréscimo de Tensões em
Maciços Elásticos Semi-Infinito
4.2.1 Carga Vertical Aplicada à Superfície do Terreno
r
2
3⋅Q   r  
=
∆σ V
1 +   
2 ⋅ π ⋅ z 2   z  
Q
z
−
5
2
Q é a carga pontual aplicada ( N ) , z
σv
(5
é a
profundidade ( m ) que vai da superfície do terreno
(ponto de aplicação da carga) até a cota onde deseja-
Figura 41 – Carga concentrada aplicada
na superfície do terreno.
se calcular ∆σ V , (em N / m 2 ), r é a distância
horizontal ( m ) do ponto de aplicação da carga até
onde atua ∆σ V .
Exemplo:
1 – Considere que uma carga concentrada de 10 kN é aplicada sobre a superfície de um solo.
Calcule o acréscimo de tensões ocasionado pela aplicação desta carga no ponto A:
96
2 – Uma carga concentrada de 30 t é aplicada na superfície do solo. Calcule o acréscimo de
tensão vertical em um ponto de coordenadas x = 1,50 m , y = 2,10 m e z = 1,10 m . O
ponto de aplicação da carga coincide com a origem do sistema de referência.
4.2.2 Carregamento Uniformemente Distribuído sobre uma Placa Retangular
a = mz
∆σ v
z
Para o caso de uma área retangular de lados a e b ,
uniformemente carregada (Figura 42), as tensões
verticais em um ponto situado numa profundidade
(z), na mesma vertical de um dos vértices, é dada pela
equação (6).
Onde σ 0 é carga por unidade de área, m = a z ,
Figura 42 – Placa retangular
uniformemente carregada.
n =b z.
1
1



2
2
2
2
2
2
2
2
⋅
⋅
+
+
⋅
+
+
2
1
2
2
m
n
m
n
m
n
m
n
(
)
(
)
σ0 
m +n +2


=
⋅
+ arc tg  2
σz
2
2
2

4π  m 2 + n 2 + m 2 ⋅ n 2 + 1 m 2 + n 2 + 1
 m + n − m ⋅ n + 1 



(6)
Pode-se observar que a equação (6) depende apenas da geometria da área carregada ( m e
n ), assim, a equação (6) pode ser reescrita em função de um fator de influência:
σ z = q ⋅ Iσ
(7)
onde Iσ é um fator de influência que depende de m e n .
Os valores de Iσ , para vários valores de m e n , podem ser mais facilmente determinados
com o uso do gráfico apresentado na Figura 43 ou usando a Tabela 11. Assim, para calcular
σ z em um ponto, sob um vértice de uma área uniformemente carregada, basta determinar
x e y e os valores de m e n , e obter Iσ , usando o gráfico da Figura 43 ou a Tabela 11.
É importante salientar que todas as deduções estão referenciadas a um sistema de
coordenadas, no qual o vértice, ou seja, o canto da área carregada coincide com a origem
dos eixos. Para calcular o acréscimo de tensões em pontos que não coincidem com o canto
da área carregada, deve-se usar o princípio da superposição dos efeitos, acrescentando e
subtraindo áreas, de tal forma que o efeito final corresponda à área efetivamente
carregada.
97
Figura 43 – Fatores de Influência para a placa retangular uniformemente carregada.
Tabela 11 – Fatores de Influência para uma placa retangular
m=a/z ou
n=b/z
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,2
1,5
2,0
2,5
3,0
5,0
10,0
0,005
0,009
0,013
0,017
0,020
0,022
0,024
0,026
0,027
0,028
0,029
0,030
0,031
0,031
0,032
0,032
0,032
0,009
0,018
0,026
0,033
0,039
0,043
0,047
0,050
0,053
0,055
0,057
0,059
0,061
0,062
0,062
0,062
0,062
0,013
0,026
0,037
0,047
0,056
0,063
0,069
0,073
0,077
0,079
0,083
0,086
0,089
0,090
0,090
0,090
0,090
0,017
0,033
0,047
0,060
0,071
0,080
0,087
0,093
0,098
0,101
0,106
0,110
0,113
0,115
0,115
0,115
0,115
0,020
0,039
0,056
0,071
0,084
0,095
0,103
0,110
0,116
0,120
0,126
0,131
0,135
0,137
0,137
0,137
0,137
0,022
0,043
0,063
0,080
0,095
0,107
0,117
0,125
0,131
0,136
0,143
0,149
0,153
0,155
0,156
0,156
0,156
0,024
0,047
0,069
0,087
0,103
0,117
0,128
0,137
0,144
0,149
0,157
0,164
0,169
0,170
0,171
0,172
0,172
m = a/z ou n = b/z
0,8
0,9
1,0
0,026
0,050
0,073
0,093
0,110
0,125
0,137
0,146
0,154
0,160
0,168
0,176
0,181
0,183
0,184
0,185
0,185
0,027
0,053
0,077
0,098
0,116
0,131
0,144
0,154
0,162
0,168
0,178
0,186
0,192
0,194
0,195
0,196
0,196
0,028
0,055
0,079
0,101
0,120
0,136
0,149
0,160
0,168
0,175
0,185
0,193
0,200
0,202
0,203
0,204
0,205
1,2
1,5
2,0
2,5
3,0
5,0
10,0
0,029
0,057
0,083
0,106
0,126
0,143
0,157
0,168
0,178
0,185
0,196
0,205
0,212
0,215
0,216
0,217
0,218
0,030
0,059
0,086
0,110
0,131
0,149
0,164
0,176
0,186
0,193
0,205
0,215
0,223
0,226
0,228
0,229
0,230
0,031
0,061
0,089
0,113
0,135
0,153
0,169
0,181
0,192
0,200
0,212
0,223
0,232
0,236
0,238
0,239
0,240
0,031
0,062
0,090
0,115
0,137
0,155
0,170
0,183
0,194
0,202
0,215
0,226
0,236
0,240
0,242
0,244
0,244
0,032
0,062
0,090
0,115
0,137
0,156
0,171
0,184
0,195
0,203
0,216
0,228
0,238
0,242
0,244
0,246
0,247
0,032
0,062
0,090
0,115
0,137
0,156
0,172
0,185
0,196
0,204
0,217
0,229
0,239
0,244
0,246
0,249
0,249
0,032
0,062
0,090
0,115
0,137
0,156
0,172
0,185
0,196
0,205
0,218
0,230
0,240
0,244
0,247
0,249
0,250
98
Exemplo: Uma construção industrial apresenta uma planta retangular com 12 m de largura
e 48 m de comprimento, e vai aplicar ao terreno uma pressão uniformemente distribuída de
50 kPa. Determinar o acréscimo de tensão a 6 m de profundidade na vertical dos pontos A,
B, C, D e E indicados na figura abaixo:
4.2.3 Carregamento Uniforme Distribuído sobre uma Placa Retangular de Comprimento
Infinito (sapata corrida)
Quando uma das dimensões de uma placa retangular for muito superior à outra
(comprimento superior a duas vezes a largura), os valores de tensão resultantes no maciço
de solo podem ser obtidos por formulação desenvolvida por Carothers & Terzaghi. O
esquema apresentado a seguir ilustra uma placa carregada uniformemente com carga q e o
ponto A onde atuam as tensões. Observar que a placa tem largura 2b e está carregada
uniformemente com q. As tensões num ponto A, situado a uma profundidade (z) e distante
(x) do centro da placa são dadas pelas equações (8), com ângulo a dado em radianos.
Figura 44 – Placa retangular de comprimento infinito (sapata corrida).
σz =
σx =
q
π
q
π
(α + senα ⋅ cos 2β )
(α − senα ⋅ cos 2β )
(8)
99
4.2.4 Carregamento Uniforme sobre uma Placa Circular
O cálculo das tensões induzidas por uma placa circular de raio r, uniformemente carregada,
foi resolvido por Love, a partir da integração da equação Boussinesq, para toda área circular.
Para pontos situados a uma profundidade z, abaixo do centro da placa de raio r, as tensões
induzidas podem ser estimadas pela equação (9)
3


2


1


∆σ z = q0 1 − 

 1 + ( r z )2  
 
 


(9)
Essa expressão, na prática, pode ser simplificada pela introdução de um fator de influência
Iσ , podendo ser reescrita na forma:
∆σ z =
q0 Iσ
(10)
O fator de influência é obtido em função da relação z/r e x/r, dada pelo gráfico da Figura 45,
onde: z = profundidade; r = raio da placa carregada; x = distância horizontal que vai do
centro da placa ao ponto onde se deseja calcular o acréscimo de tensões; qo = pressão de
contato. Observar que neste gráfico os fatores de influência são expressos em porcentagem.
Para obtenção dos valores de Iσ , para pontos quaisquer do terreno, também se pode
utilizar a Tabela 12. Vale acrescentar que quando tem-se x/r = 0, tem-se o acréscimo de
tensões induzida na vertical que passa pelo centro da placa circular carregada.
Tabela 12 – Fatores de Influência para uma placa circular de raio r
z/r
0,25
0,50
0,75
1,00
1,25
1,50
1,75
2,00
2,50
3,00
4,00
5,00
7,00
10,00
0,00
0,25
0,50
1,00
x/r
1,50
2,00
2,50
3,00
3,50
4,00
0,986
0,911
0,784
0,646
0,524
0,424
0,346
0,284
0,200
0,146
0,087
0,057
0,030
0,015
0,983
0,895
0,762
0,625
0,508
0,413
0,336
0,277
0,196
0,143
0,086
0,057
0,030
0,015
0,964
0,840
0,691
0,560
0,455
0,374
0,309
0,258
0,186
0,137
0,083
0,056
0,029
0,014
0,460
0,418
0,374
0,335
0,295
0,256
0,223
0,194
0,150
0,117
0,076
0,052
0,028
0,014
0,015
0,060
0,105
0,125
0,135
0,137
0,135
0,127
0,109
0,091
0,061
0,045
0,026
0,013
0,002
0,010
0,025
0,043
0,057
0,064
0,071
0,073
0,073
0,066
0,052
0,039
0,024
0,013
0,000
0,003
0,010
0,016
0,023
0,029
0,037
0,041
0,044
0,045
0,041
0,033
0,021
0,013
0,000
0,000
0,002
0,007
0,010
0,013
0,018
0,022
0,028
0,031
0,031
0,027
0,019
0,012
0,000
0,000
0,000
0,003
0,005
0,007
0,009
0,012
0,017
0,022
0,024
0,022
0,016
0,012
0,000
0,000
0,000
0,000
0,001
0,002
0,004
0,006
0,011
0,015
0,018
0,018
0,015
0,011
100
Figura 45 – Fatores de Influência, expresso em %, para a placa circular uniformemente carregada.
101