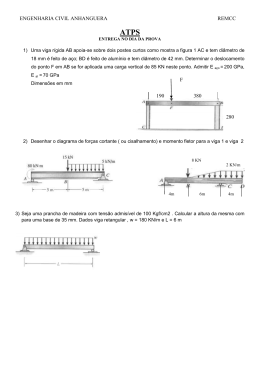
CIV 1127 – ANÁLISE DE ESTRUTURAS II – 2º Semestre – 2002
Segunda Prova – 30/10/2002 – Duração: 2:30 hs – Sem Consulta
1ª Questão (5,5 pontos)
Empregando-se o Método dos Deslocamentos,
obter o diagrama de momentos fletores para o
quadro ao lado (barras inextensíveis). Todas as
barras têm a mesma inércia à flexão EI = 3,6x104
kNm2, com exceção da barra vertical superior que
é infinitamente rígida à flexão.
2ª Questão (1,5 pontos)
Considere a viga abaixo cujo apoio da esquerda
sofreu um recalque vertical de 4 cm para baixo.
As barras têm inércia à flexão EI = 3,6x104
kNm2. Utilizando a Analogia da Viga Conjugada
(vide tabela ao lado), determine o diagrama de
momentos fletores.
A
B
C
Analogia da Viga
Conjugada
VIGA
REAL
VIGA
CONJUGADA
Carregamento
q(x)
qc(x) = M(x)/EI
Esforço Cortante
Q(x)
Qc(x) = θ(x)
Momento Fletor
M(x)
Mc(x) = v(x)
Rotação
θ(x)
Deslocamento
Transversal
v(x)
3ª Questão (2,0 pontos)
Empregando-se o Método das Forças, obter os
diagramas de momentos fletores e momentos torçores para a grelha ao lado. A relação entre a rigidez à torção e a rigidez à flexão é GJt = 6EI,
para todas as barras.
4ª Questão (1,0 ponto)
Grau vindo do segundo trabalho (nota do trabalho x 0,1).
1ª Questão
Sistema Hipergeométrico (SH)
1
2
caso (1) – Deslocabilidade D1 isolada no SH
caso (0) – Solicitação externa isolada no SH
0
β10 = + 36 kNm
D1 = 1
K11 = +2EI
+36
–36
+36
⇑
(ΣFx=0)
β20 = – 12 kN
0
K21 = +7EI/9
0
M0
⇑
(ΣFx=0)
[kNm]
0
2EI
6·3
0
(36÷3=12)
+4EI
6
+4EI
3
+2EI
3
0
M1
+2EI
6
–2EI
6
0
x D1
0
6EI
32
Sistema de Equações de Equilíbrio
 β 10 + K 11 D1 + K 12 D2 = 0

β 20 + K 21D1 + K 22 D2 = 0
caso (2) – Deslocabilidade D2 isolada no SH
8EI
9·3
0
D2 = 1
K12 = +7EI/9
+2EI
θ2 = 1/3
6
K22 = +26EI/27
–8EI
9
θ2
+6EI
32
⇑
(ΣFx=0)
M2
+4EI θ2
6
+6EI
32
+3EI θ2
+ 3EI
3
32
x D2
0
+3EI θ2
+ 3EI
32
33
12EI
33
Momentos Fletores finais
M = M 0 + M 1 D1 + M 2 D2
0
+18.2
–18.2
+4.0
–38.3
+12.1
+26.2
M
[kNm]
M
0
[kNm]
+ 7 / 9  D1  0
 +2
+ 36
 + EI ⋅ 

⋅  =  
− 12 
+ 7 / 9 + 26 / 27  D2  0
33.308

−3
D1 = − EI = −0.925 ⋅ 10 rad
⇒
39.364
D2 = +
= +1.093 ⋅ 10 − 3 m
EI

2ª Questão
VIGA REAL
VIGA CONJUGADA
MC
ρ = 0.04 m
VA
vA =-ρ
θA ≠ 0
ρ
VC
VB
a=6m
MB/EI
b=4m
vB = 0
vC = 0
θB esq
= θBdir
θC = 0
MC/EI
MCc = 0
QCc = 0
MBc = 0
QBc esq
= QcBdir
MAc =-ρ
QAc ≠ 0
b/3
2a/3
MB⋅a/2EI
MB/EI
MB⋅b/2EI
ρ
Diagrama de momentos fletores:
–MB
–
MC/EI
a
–
+
M(x)
+MC
x
2b/3
MC⋅b/2EI
MBc = 0 ⇒ MC = MB / 2
ΣMAc = 0 ⇒
M a 2a M b 
b M b 
2b 
ρ − B ⋅ − B ⋅ a +  + C ⋅a +  = 0
2 EI 3
2 EI 
3  2 EI 
3 
EI = 3.6x104 kNm2
ρ = 0.04 m a = 6 m b = 4 m
∴
MB = 80 kNm
MC = 40 kNm
3ª Questão
Sistema Principal (SP) e
Hiperestático (g = 1)
caso (0) – Solicitação externa isolada no SP
180
T0 [kNm]
M0 [kNm]
X1
20
20
60
0
180
20
20
+60
60
+60
60
60
caso (1) – Hiperestático X1 isolado no SP
M1
T1
3
0
0
X1 = 1
0
x X1
–6
X1 = 1
3
–3
3
6
Equação de Compatibilidade:
1
1
1
1
1
1
 1
 1
δ 10 = − ⋅ 3 ⋅ 60 ⋅ 3 + ⋅ 6 ⋅ 60 ⋅ 6 − ⋅ 6 ⋅ 180 ⋅ 6 − ⋅ 3 ⋅ 60 ⋅ 6 + ⋅ 3 ⋅ 60 ⋅ 6 + ⋅ 3 ⋅ 180 ⋅ 6 − ⋅ 3 ⋅ 180 ⋅ 6 ⋅
6
3
6
3
3
6
 3
 EI
1
2700 7560
2700 7560
3960
+ [( −3) ⋅ (60 ) ⋅ 6 + ( −6 )(180) ⋅ 6]⋅
=−
−
=−
−
=−
GJ t
EI
GJ t
EI
EI
6EI
1
99 270 99 270
144
 1
 1
 1
δ 11 = 3 ⋅  ⋅ 3 ⋅ 3 ⋅ 3  + ⋅ 6 ⋅ 6 ⋅ 6 ⋅ + [( −3) ⋅ ( −3) ⋅ 6 + ( −6 ) ⋅ ( −6) ⋅ 6]⋅
=
+
=
+
=+
3
3
EI
GJ
EI
GJ
EI
EI
EI
6


 
t
t
δ 10 + δ 11 X 1 = 0 ⇒
X1 = +27.5 kN
Momentos Fletores e Momentos Torçores finais
M = M0 + M 1X1
M [kNm]
97.5
T
60
0
22.5
15
22.5
60
T = T0 + T1 X 1
+60
–22.5
[kNm]
+15
+180