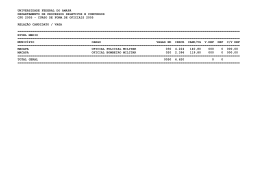
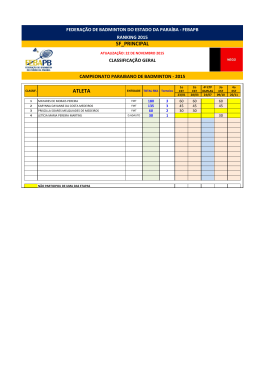
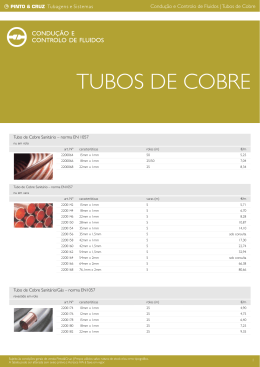
Aula Teórica de 02 – 11 – 2000
Estruturas Hiperestáticas
Aplicação do princípio da sobreposição dos efeitos na determinação do estado de tensão e de
deformação de uma estrutura hiperestática sujeita à acção de uma variação de temperatura, um
defeito de fabrico ou um assentamento de apoio.
Professor Luis Juvandes
FEUP - ENGENHARIA CIVIL
Folha 1/3
RESISTÊNCIA DE MATERIAIS 1
∆t ; δ apoio ; ∆ def . fabrico
ACÇÕES:
MÉTODO: criação de 1 apoio fictício ⇒
Ano lectivo 2000/2001
FASE I
+
FASE II
VARIAÇÃO DE TEMPERATURA [∆t]
FASE I
=
CORPO
D
B
R
CORPO
D
tB
E
+
FASE II
+
CORPO
R
tE
R
C
C
EST. HIPER.
EST. FIXA
(apoio fictício)
R = α ∆t EA
Fase I
N
N
I
DE
I
BC
1 Eq. Equil.
Fase II 1Eq. Comp. Def.
= +R
=0
↓
δIB = 0
N IIDE = ...
N IIBC = ...
δ IIB = ...
PRINCÍPIO DA SOBREPOSIÇÃO
DOS EFEITOS (P.S.E)
N DE = N DE + N DE
I
II
N BC = N BC + N BC = N BC
I
II
II
δB = δB + δB = δB
I
Professor Luís Juvandes
II
II
Aula 02/11/2000
FEUP - ENGENHARIA CIVIL
Folha 2/3
RESISTÊNCIA DE MATERIAIS 1
Ano lectivo 2000/2001
ASSENTAMENTO DE APOIO [δc]
+
FASE I
=
CORPO
D
A
B
E
C
C’
+
CORPO
D
A
R
FASE II
CORPO
D
A
R
B
B
E
C
C
C
= 1mm
E
C’
C
R
EST. HIPER.
EST. FIXA
(apoio fictício)
EA
δc
I
Fase I N BC = + R
I
N DE = φ
I
δB = 0
R=
P.S.E.
→
N BC = N BC + N BC
I
Professor Luís Juvandes
1 Eq. Equilib.
1 Eq. Comp. Def.
↓
N BC = ...
II
N DE = ...
II
δ B = ...
II
II
N DE = N DE + N DE = N DE
I
II
II
δB = δB + δB = δB
I
Fase II
II
II
Aula 02/11/2000
3.0
P
C
d) a combinação das três acções referidas nas alíneas anteriores.
B
Dados:
FEUP - ENGENHARIA CIVIL
A
a) uma carga P = 100 kN.
b) uma diminuição de temperatura da barra BE de 20ºC.
c) um assentamento vertical do apoio D, D = 1mm.
RESISTÊNCIA DE MATERIAIS 1
Professor Luís Juvandes
Considere a estrutura representada na figura, constituída por um corpo infinitamente rígido ABC e pelas
barras deformáveis CD e BE. Calcule os esforços axiais nas barras CD e BE e o deslocamento do ponto
C para:
3.0
BE: E = 200GPa ; A = 20cm2
D
CD: E = 200GPa ; A = 10cm2
= 1.2 x 10-5 / ºC
2.0
N CD I =
Solução
c)
⊕
II
N CD II = −47.70kN
N BE II = −35.77kN
δ C, V II = δ C ,H / 0.75 = 0.7155mm(↓)
δ C, H II = δ B II = 0.536mm(→)
2.0
NC D = 18.97kN
⇔
NB E = −35.77kN
II
II
δ c = δ c II δ C , V δ C ,H
3.0
[m]
Folha 3/3
Aula 02/11/2000
Ano lectivo 2000/2001
200
kN
3
I
I N BE = 0
δc I = 0
E