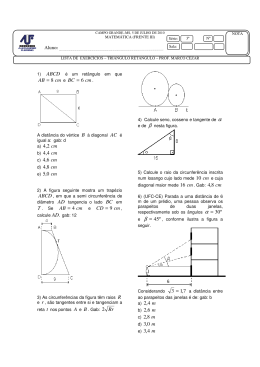
Reforço Orientado
Matemática –Ensino Médio
Aula 4 - Potenciação
Nome: __________________________________________________________ série: __________ Turma: _________
Exercícios de sala
1) Calcule as potências, em cada quadro:
Quadro A
a) 73
1
 71 
s)   
 15 
2
Quadro B
 2
d)   
 5
a) 10-2
2
b) (-2)-2
e) (-1,1)2
3
c)  
4
f) 103
g) (-4)3
4
h)  
7
3
 2
d)   
 3
2
2
e) (0,1)-2
 1
i)   
 6
f) 4-2
3
g) (-3)-2
j) (3,14)1
k) 1
3
t) (0,2)4
b) (-3)2
3
c)  
2
 1
r)  
5
 1
h)  
5
5
6
l) (-1)
1
 16 
m) 

 713 
 3 
n)   
 10 
4
0
o) (-1,71)
p) 09
0
q) (-10)
3
 1
i)   
 4
3
j) (0,5)-1
k) 6
-3
l) (-1)-4
6
m)  
7
2
 3
n)   
 7
2
o) (1,5)-1
5) Calcule as potências.
p) 1-5
a) (0,2)2
q) (-2)-5
 10 
r)  
 9 
b) (1,3)2
1
c) (-1, 3)2
 13 
s)   
 10 
1
d) (-3)3
e) (0,7777...)0
t) (0,25)-2
3
f)  
4
2
2) Devido ao desgaste, o valor de um carro vai
diminuindo com o tempo. A cada ano que passa, o
g) 04
valor fica multiplicado por 0,8. Se hoje o carro vale
h) 106
R$ 20 000,00, quanto valerá daqui a 3 anos?
i) (1,4)2
j) 110
k) (-1)10
2
l)  
7
3) Calcule 100 (1,2)n para:
2
a) n = 0
 13 
m)  
 3 
b) n = 1
n) (0,1)
0
3
c) n = 2
5
o) (0,2)
d) n = 3
p) (1,333...)1
5
q)  
6
4) Vamos calcular o valor de:
3
2
a) x – x – x +1, para x = -1
b) 10x2 + 100x – 1 000, para x = 5
3
r)  
4
3
2
4
s)  
9
1
t) (0,1)-1
6) Calcule o valor de:
 1
a) 3 – 23 +  
2
10) No vácuo, a luz percorre 300 000 km a cada
segundo. Um ano-luz é a distância que a luz percorre
0
2
em um ano.
3
b) 4 . 23 -   . (-2)1
2
a) Expresse um ano-luz em quilômetros, na notação
c) 51 . 3-2 + 3-1 – 3 . 30
decimal.
científica. Aproxime o coeficiente usando uma casa
b) A quantos quilômetros da Terra está uma estrela
d) 23 – 2 . 32
10
que dela dista 6 anos-luz?
5
6
e) (-1) + 3 . (-1) – 3 . (-1)
f) (+5)4 – (-5)4
11) Aplique as propriedades das potências:
2
3
-1
a) a . a . a
b) 108 : 105
7) Calcule:
2
a) x – 5x + 10, para x = 2
c) a . b . c
b) 3x2 + 4x – 1, para x = 0,5
d) (a . x)2
c) x2 + 3x + 1, para x = 0,1
e) a5 : a2
d) 2x3 – x2 – x + 2, para x = -1
8) Calcule, expressando o resultado em notação
10
a
f)  
2
10
10
3
científica:
 2  a2 
g) 

 5 
a) (1,25 . 104) . (6. 108)
h) (x5)-3
3
b) (4,5 . 107) : (2,5 . 104)
-2
-6
c) (3,2 . 10 ) . (1,5 . 10 )
4
6
d) (6 . 10 ) . (5,5 . 10 )
12) Na tabela é dada a decomposição em fatores
primos do inteiro p. Copie e complete escrevendo a
decomposição do inteiro n, sendo n = p2.
9) Calcule, reduzindo a uma só potência:
3
a) 10 . 10
Decomposição em fatores primos
2
De p
8
b) 10 : 10
De n = p
5
3
4
c) 2 . 5
2
?
2 .3 .5
?
2ª . 3b . 5c . 7d
?
2 .3.7
4
5
d) 2-2 . 3-2 . 5-2
3
e) 60 : 12
3
f) 2504 : 1254
2 3
g) (2 )
2
2
13) Verdadeiro ou falso? (Faça os cálculos, se
necessário.)
e)
a3
b3
5 2
2 -3
f) (2 )  (2 )
a)
102  104
 103
3
10
g) 52  x2
h)
b) (2x)10 = 2x10
2
2
c) (5 . 3) = 5 . 3
2
2
2
d) (5 : 3) = 5 : 3
i)
2
2
f) (5 – 3) = 5 – 3
a 2b 2
c2
j) (10-1)3 : (102)-2
e) (5 + 3)2 = 52 + 32
2
54  5
53
2
18) Calcule as expressões:
14) Qual é o número maior?
a) 2 – 3  2
a) 3,2 . 106 ou 8,4 . 105
b) 130 – 3  23
b) 6,6 . 10-11 ou 3,9 . 10-12
c) 104 + 2  103 - 6  102 – 17  101 + 100
5
2
d) 2 . 35 - 5  32 + 6  31 - 7  30
15) Qual é o número menor?
2
a) 2,5 . 10-3 ou 8 . 10-2
 1
e) 3-1 -  
3
b) 9,9 . 1021 ou 1,1 1023
f) (2-2 – 4-2) . (2-1 + 4-1)
2
2
2
g) (12 + 10) – (12 + 10 )
Exercícios Propostos
16) Calcule e responda usando a notação cientifica:
a) (8  1015) : (2  1012)
h) (12 . 10)2 – (122 .102)
19) Que número positivo deve ser colocado no lugar do ?
a) (?)2 = 100
3
b) (4,5  10 ) (9,2  10 )
b) (?) = 64
c) (2,25  10 ) : (9  10 )
c) (?) =
6
4
4
6
d) (2  10-3) (5  10-8)
2
4
9
2
d) (?) = 144
e) (?)3 = 27
17) Aplique as propriedades e reduza a uma só
f) (?)3 =
potência:
a) 10  10
6
4
6
4
b) 10 : 10
2 4
c) (x )
d) 34  24
1
8
g) (?)3 = 1
h) (?)2 = 0,04
20) Qual é o expoente?
B
a) 10? = 100 000
a) 101
b) 10? = 0,001
b) 100
?
c) 2 = 64
7
c)  
3
d) 7? = 343
0
?
 3 
e)    0,09
 10 
1
 1
d)   
 5
?
3
f)    1
4
0
e) (1,7)
f) 010
21) Calcule as potências em cada cartão:
 2
g)   
 3
0
A
h) 03
a) 53
2
i) 30
3
j) (-3,14)
b) (-6)
0
c) (-4)
d) (-3)5
C
e) (0,25)2
a) 8-2
f) (0,2)3
b) 6
2
g)  
3
-1
3
-3
c) (-2)
 1
h)   
 2
 1 
i)  
 10 
4
3
 1
j)   
 10 
 1
d)   
 4
3
e)  
8
2
1
2
 2
f)   
 5
3
-23
22) Calcule as expressões:
28) Uma molécula de sal de cozinha pesa 9,7 x 10 g.
a) (0,25)2 – (0,5)3
Quantas moléculas existem em 1 kg de sal? Responda
3
na notação científica (a x 10 n, sendo 1  a  10 ).
2
 1
 1
b) 3    5     5  21  3  20
2
 
 2
2
c) (7 – 5,5)
29) Reduza a uma só potência:
d) (22 + 2-2)2
 1
a)  
5
n
2n
3n
2
5
 1  1
   
5 5
23) Calcule o valor de (-1) + (-1) + (-1) , sendo:
b) (-7) 12 . (-7)4
a) n ímpar
 2 2   2 3
c)    :  
 3    3 
4
b) n par
3
 1  1
 2  2
 

d) 
2
 1 3 
   
 2  
24) Simplifique as expressões:
a)
1
a1  b1
a1  b1
2
b) (x-1 + y-1) (x + y)-1
30) Simplifique:
a) (a2b-1)4 . (a-1b2)-2
25) Calcule:
b) 2ab : a-2
a) (2,5 x 1012) (4,0 x 109)
b) (3,6 x 10-4) (5,5 x 10-5)
c)
c) (1,2 x 108) (8,2 x 10-5)
15
a3  a5
a  a4
d) (32)23
10
d) (4,0 x 10 ) : (8,0 x 10 )
31) Na reta numérica estão assinalados alguns pontos:
26) Responda:
5
5
a) Por quanto devemos multiplicar 3 para obter 6 ?
b) Por quanto devemos dividir 10 12 para obter 512?
27) Tendo em vista que 210  103 , faça a aproximação,
Entre quais pontos consecutivos deve ser assinalado o
usando potências de 10:
a) 260
b) 264
número resultante do cálculo de
104 n  103  10n
?
104  10n
4
-1
-1
32) Calcule o valor de 3x – 2x + 4x , para x = 10 . Dê
36) Calcule as potências em cada cartão:
A
a resposta na forma decimal.
a) 25
4
33) Calcule as expressões seguintes e responda: Qual
b) (-3)
tem o maior valor? E o menor?
c) (-7)3
a) 0
25
0
4
+ (-25) + (-1)
1
3
 1
b)  1     ( 2)1
 2
c)
101
5  21
d)
42  42
42  42
e)
3
 1
e)   
 2
3
1
B
a) (0,9)2
82  42
81  41
b) (0,1)3
2   2    2 
1
1
f)
3
d)  
4
2
1  22
c) (1,5)2
d) (-2,5)2
e) (-0,3)3
34) Calcule:
C
a) (0,5)3 – (0,75)2
b) (0,4)2 + 2 . (1,2)2
a) 70
c) 4 . (2,5)2 – 8 . (1,5)2
3
b)  
5
35) Quanto é o expoente?
a) 2? = 128
1
b) 3? =
9
2 9
c)   
3 4
d) 4? = 1
e) 10? = 1 000
f) 10? = 0,1
1
c) 4
-2
d) 5
-3
e) (-3)-2
D
a) (-5)-1
3
b)  
4
2
 1
c)   
 2
3
d) (0,1)-1
e) (-1)11
43) Reduza a uma só potência, aplicando as
2
37) Qual é maior: 53 ou (53 )2 ?
38) Por quanto devemos multiplicar 5
10
para obter
a) a2 . a5 . a
10
10 ?
39) Simplifique:
b)
a) x2 . x3 . x4
b)
propriedades:
108
103
c) 23 . a3 . b3
76
72
d)
25
35
c) (a3)3 . a-2
-5 -2
e) (a )
d)
112  114
113
3
f)
5 a
e)  3a    
3
4
2
3
 1  2  1
f)        
2 3 3
3
2
 c   1
 3   
a  b
4
 xy 2   x 2 y 
b) 
 

 2   4 
3
a) n ímpar
2
b) n par
2
+2
n+2
x2 y2  x3 y
para x = 0,5 e y = 1,5.
y2  x2
46) Calcule: (-1)n+3 – (-1)n+2 – (-1)2n+1 – (-1)2n-1, sendo:
a) 2n+3 é quantas vezes 2n?
n+1
28
2
41) Responda às questões:
n
 24
45) Calcule
2 2
 3xy   2x y   16x 
c) 

 :


 4   3   9y 
b) 2 + 2
2
44) Calcule x, de modo que 102x-4 = 1.
2
40) Simplifique as expressões:
 a2b 
a) 

 c 
2 
n
é quantas vezes 2 ?
42) Como 210 = 1 024, em algumas situações usamos
a aproximação 210  103. Um multimilionário decidiu, no
dia 30 de abril, fazer uma doação de 2 30 reais para
1 000 instituições de caridade no mundo. Quanto
recebeu cada uma, aproximadamente?
GABARITO:
Exercícios de sala
2) Gab: R$ 10 240,00
1) QUADRO A
QUADRO B
3) Gab:
a) 343
1
a)
100
a) 100
b) 9
c)
9
4
1
4
b)
b) 120
c) 144
d) 172,8
4
25
d)
e) 1,21
f) 1 000
g) –64
16
h)
49
c)
64
27
d)
9
4
4) Gab:
a) 0
b) –250
e) 100
s)
9
4
t) 10
6) Gab:
a) –13
b) 35
c) 
19
9
d) –10
e) –5
5) Gab:
f) 0
1
f)
16
a) 0,04
b) 1,69
7) Gab:
a) 4
1
g)
9
c) 1,69
h) 125
d) –27
i) –64
e) 1
k) 1
j) 2
9
f)
16
8) Gab:
l) 1
k)
g) 0
a) 7,5 · 1012
h) 1 000 000
b) 1,8 · 103
i) 1,96
c) 4,8 · 10
j) 1
d) 3,3 · 10
k) 1
9) Gab:
i) 
1
216
j) 3,14
16
m)
713
n)
81
10000
o) 1
1
216
q) 1
1
r)
125
71
s) 
15
t) 0,0016
c) 1,31
d) 0
l) 1
m)
49
36
n)
49
9
l)
p) 0
b) 1,75
o)
2
3
p) 1
q)
1
32
9
r)
10
s) 
10
13
t) 16
49
4
–8
a) 9,5 · 10
b) 103
m) 1
c) 104
n) 0,001
d) 30–2
o) 0,00032
e) 53
p) 1,333...
f) 24
q)
125
216
g) 26
r)
16
9
11
5
10) Gab:
a) 10
15) Gab:
g) 240
–3
12
a) 2,5 · 10
b) 5,7 · 1013
b) 9,9 · 10
i)
1
1000
j)
1
100
h) 0
21
19) Gab:
11) Gab:
a) 10
B
4
a) a
Exercícios propostos
b) 4
16) Gab:
2
c)
3
a) 10
b) 10
3
10
c) (a · b · c)
2
a) 4 · 10
2
d) a · x
b) 4,14 · 10
e) a3
f)
3
c) 2,5 · 10
a3
8
d) 1 · 10
10-10)
11
–3
–10
(ou apenas
b) 1
c) 1
d) 12
e) 3
d) 
1
2
e) 1
f)
f) 0
17) Gab:
g) 1
a) 1010
h) 0,2
h) x
b) 102
20) Gab:
12) Gab:
c) x8
6
g)
8a
125
–15
Decomposição em fatores
primos
De p
De n = p2
26 · 32 · 74
23 . 3 . 7 2
5
10
2
4
d) 64
a
e)  
b
3
2 ·3 ·5
2ª . 3b . 5c
. 7d
22a · 32b · 52c
2d
·7
g) (5x)2
h) 5
 ab 
i)  
 c 
13) Gab:
a) V
j) 10
c) V
a) 14
b) –23
e) F
c) 11231
f) F
d) 452
14) Gab:
b) 6,6 · 10
6
j) 1
17
e)
9
–11
9
f)
64
C
c) 26
a)
1
64
b)
1
6
2
0
21) Gab:
c) 
e)
64
9
f)
125
8
a) 25
b) 36
1
8
d) –4
A
1
18) Gab:
a) 3,2 · 10
b) 10-3
2
b) F
d) V
i) 1
4
f)  
3
2
h) 0
a) 105
 3 
e)  
 10 
2
2 .3 .5
g) 1
d) 73
f) 24
1
5
c) –64
d) –243
e) 0,0625
f) 0,008
g)
8
27
h)
1
16
22) Gab:
a) –0,0625
b)
19
8
c) 2,25
d)
289
16
31) Gab: 0,9 – entre A
eB
23) Gab:
a) –1
e)
32) Gab: 39,8003
b)
1
xy
a) 10
a)
b) 0,001
b) –1
c) 2,25
b) y6
d) 6,25
c)
e)
–8
3
8
41) Gab:
C
a) 8
b) 7
3
b)
5
d) 5 · 104
26) Gab:
34) Gab:
a) 25
a)
c)
27) Gab:
a) 1018
1
16
d)
1
125
76
b)
25
e)
1
9
29) Gab:
4
b) (–7)16
1
· 1025
a) 27
a)
2
c)  
3
2
a10
a) 3
b
3
e) 103
36) Gab:
A
a) 32
b) 81
c) a–3
c) –343
d)
27
64
5
e) a10
1
5
f) 22
b)
16
9
45) Gab:
c) –8
46) Gab:
d) 10
b) 2a b
d) 316
2
d)  
3
0
f) 10–1
30) Gab:
3
c) (2 · a · b)
44) Gab: x = 2
11
d) –2
b) 105
b) 3–2
d) 4
2
c)  
3
a) a8
D
35) Gab:
um
43) Gab:
c) 7
19,2
28) Gab:
moléculas
42) Gab: Cada
recebe 106 reais
7
16
b) 212
16y 2
27
a) 1
16
f)
3
a) 5
e) –0,027
255
d)
257
c) 9,84 · 103
b) 10
1
7
22
b) 1,98 · 10
b5
c
a) 2
c) 0,14 =
25) Gab:
–1
40) Gab:
a) 0,81
24) Gab:
ba
a)
ba
f) 6
B
b) 3
33) Gab:
e) 33 · a
1
8
a) 4
e) –1
b) 0
37) Gab: 59 > 56
38) Gab: 2
39) Gab:
a) x9
b) 7
4
c) a1
d) 113
10
15
 0,1875
80