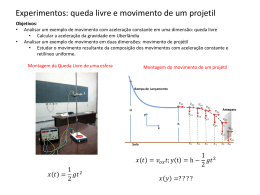
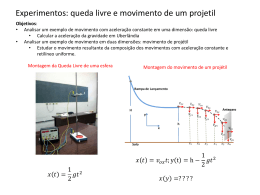
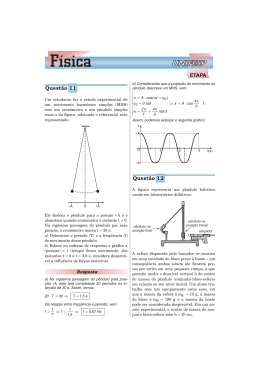
FUNDAÇÃO ESCOLA TÉCNICA LIBERATO SALZANO VIEIRA DA CUNHA
Roteiro para Aula Prática de Física
Prof.:
Curso:
Data: ____/____/____
Sala :
Turma:
Aluno:
n°:
Roteiro elaborado pelo Professor Ernest Julius Sporket
LENTE CONVERGENTE
Objetivo: Determinar a distância focal de uma lente convergente com auxílio de luz solar.
A figura 1 mostra como um feixe de raios paralelos atravessa uma lente convergente. Quando os raios são
paralelos ao eixo principal, o triângulo ABF é uma seção de um cone cujo vértice é o foco e cuja base é a própria lente. Além disso, o triângulo é isóscele e OF é a sua altura.
A
f
A’
O
F
B’
B
Nesse trabalho os raios paralelos são os raios solares. Colocando a distância d da lente um anteparo, vai
observar um círculo claro rodeado por um anel escuro.
1 - Como você explica isso?
Se o anteparo não estiver perpendicular ao eixo principal não se forma um círculo no anteparo, mas sim
uma outra seção cônica. O diâmetro do circulo claro mede A`B`. Os triângulos ABF e A`B`F são semelhantes,
isso permite estabelecer a equação :
f
f −d
=
AB A' B'
medindo AB, A`B` e d pode calcular a distância focal.
Para conseguir que os raios solares sejam perpendiculares ao anteparo coloque-o no sol e apoie um dos catetos de um esquadro sobre o anteparo, gire o anteparo até que o outro cateto não mais projete sombra sobre o
anteparo. Mude a posição do esquadro e altere a inclinação do anteparo até que o esquadro pare de projetar
sombra sobre o anteparo. Se os raios solares são perpendiculares a duas retas de um plano eles são perpendiculares ao plano.
Coloque agora a lente defronte o anteparo e altere a sua posição até que a mancha clara no anteparo se
torne um círculo. Faça as medidas necessárias. Não coloque o anteparo no lugar do foco pois pode danificá-lo.
Espera-se que você tenha boa vontade e colabore na conservação do material.
Diâmetro da lente =
Diâmetro do circulo claro =
Distância da lente até o anteparo =
Conclusão:
PDF created with pdfFactory trial version www.pdffactory.com