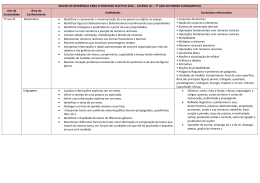
Índice
Prefácio
9
Capítulo 1
Derivadas
11
Capítulo 2
Primitivas
2.1. Noção de primitiva. Propriedades elementares
33
2.2. Primitivas imediatas
35
2.2.1. Função Potência
38
2.2.2. Funções logarítmicas
39
2.2.3. Funções exponenciais
40
2.2.4. Funções trigonométricas
41
EXERCÍCIOS RESOLVIDOS
44
EXERCÍCIOS PROPOSTOS
95
2.3. Primitivação por partes
114
2.3.1. Produto de uma função polinomial por uma função exponencial
115
2.3.2. Produto de uma função polinomial por uma função seno
ou uma função coseno
120
2.3.3. Produto de uma função polinomial por uma função hiperbólica
123
2.3.4. Produto de uma função polinomial por uma função logarítmica
125
2.3.5. Produto de uma função polinomial por uma função circular inversa
130
2.3.6. Produto de uma função exponencial por uma função trigonométrica
ou hiperbólica
132
2.3.7. Outros tipos de funções primitiváveis por partes
135
EXERCÍCIOS PROPOSTOS
147
2.4. Primitivação de funções racionais
154
2.5. Primitivação por substituição
202
x
210
2.5.2. Funções racionais em a x
221
2.5.3. Funções racionais em funções logarítmicas
224
2.5.4. Funções racionais em funções trigonométricas
e em funções hiperbólicas
228
2.5.5. Racionalização de funções irracionais
232
EXERCÍCIOS PROPOSTOS
254
2.5.1. Funções racionais em e
Capítulo 3
Integrais
3.1. Integral definido
EXERCÍCIOS PROPOSTOS
3.2. Integral indefinido
EXERCÍCIOS PROPOSTOS
3.3. Integral impróprio
271
295
299
322
325
3.3.1. Definição e cálculo
325
EXERCÍCIOS PROPOSTOS
346
3.3.2. Critérios de convergência/divergência
352
EXERCÍCIOS PROPOSTOS
383
3.4. Aplicações
388
3.4.1. Cálculo de áreas planas limitadas
388
3.4.2. Cálculo de áreas planas não limitadas
403
EXERCÍCIOS PROPOSTOS
415
3.4.3. Tópicos sobre outras aplicações
421
3.4.3.1. Comprimento de uma linha
3.4.4.2. Volume de um sólido de revolução gerado por rotação
de uma área plana em torno dos eixos coordenados
Referências Bibliográficas
421
424
426