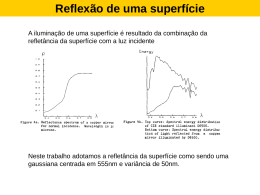
Sistema XYZ
No sistema Yxy, as diferenças não são uniformes:
Sistema L*u*v*
O sistema L*u*v* (1976) é obtido a partir de XYZ:
L*=100(Y/Yn)1/3-16
Un*=13L*(u*-un*)
Vn*=13L*(v*-vn*)
Onde:
4X
4 X + 15Y + 3Z
9Y
v* =
X + 15Y + 3Z
u* =
E=((L*)2+(u*)2+(v*)2)
4 Xn
un* =
4 Xn + 15Yn + 3Zn
9Yn
vn* =
Xn + 15Yn + 3Zn
Sistema L*u*v*
Sistema L*a*b*
O Sistema CIE L*a*b* (1976) também é uniforme:
L*=116 (Y/Yn)1/3 - 16
a*=500 ((X/Xn)1/3 - (Y/Yn)1/3)
b*=200 ((Y/Yn)1/3 - (Z/Zn)1/3)
A diferença entre duas cores se dá pela relação:
E=((L*)2+(a*)2+(b*)2)1/2
Obs.: Xn, Yn e Zn correspondem ao branco
nominal.
Sistema L*a*b*
L* = 100
L* = claridade (100 a 0)
+a* = vermelho
- a* = verde
+b* = amarelo
- b* = azul
+ b*
- a*
+ a*
- b*
L* = 0
Sistema L*C*h
Associadas ao sistema L*a*b* existem as seguintes
variáveis:
Luminosidade:
L*=116 (Y/Yn)1/3 - 16
Saturação:
C*=(a*2+b*2)1/2
Ângulo de Tonalidade:
h=arc tg (b*/a*)
Que definem o sistema L*C*h
Sistemas L*a*b* e L*C*h
Diferenças de cor
• Para a determinação de diferenças de cor usa-se o
parâmetro E:
E
*
ab
= ( L* )2 + ( a* )2 + ( b* )2
• Para a determinação de diferenças de tonalidade usase o parâmetro H:
*
* 2
* 2
* 2
Hab



= ( Eab ) ( L ) ( Cab )
Diferenças de cor
E
Diferença de cor
< 0,2
imperceptível
0,2 a 0,5
muito pequena
0,5 a 1,5
pequena
1,5 a 3,0
distinguível
3,0 a 6,0
facilmente distinguível
6,0 a 12,0
grande
> 12,0
muito grande
Norma CIE 1994
Apesar do espaço CIE L*a*b* de 1976 ser uniforme, a
percepção de diferenças de cor no seu interior não é
uniforme, o que levou a CIE a criar o parâmetro E*94
 L
E = 
 kL .SL
*
*
94
Onde:
  C
 + 
  kC .SC
2
SL = 1
*
SC = 1 + 0,045Cab
*
SH = 1 + 0,015Cab
kL = kC = kH = 1
*
ab
  H
 + 
  kH .SH
2
*
ab



2
Norma CIE 1994
Como o valor de E*94 depende do valor de C*ab,
normalmente usa-se o valor do padrão. Quando nenhuma
das amostras pode ser considerada como padrão, usa-se a
média geométrica entre ambas:
SL = 1
*
*
SC = 1 + 0,045 Cab
.
C
,1 ab, 2
*
*
SH = 1 + 0,015 Cab
.
C
,1 ab, 2
Norma CIE 1994
Em algumas aplicações pode ser interessante alterar os
parâmetros colorimétricos kL, kC ou kH. Neste caso a
notação deve ser:
E*94(kL,kC,kH)
Na indústria têxtil é comum usar kL=2, de forma que a
notação a ser usada é:
E*94(2,1,1)
Norma CMC
O ECMC é similar ao E*94:
ECMC
 L   C   H 
 + 
 + 

= 
 l.SL   c.SC   SH 
*
*
SL = 0.040975L

1 + 0.01765L*

 SL = 0.511
2
, L* > 16
, L*  16
*
0.0638C
=
+ 0.638
SC
*
1 + 0.0131C
SH = ( FT +1 - F )SC
*
2
*
2
Na indústria têxtil utiliza-se
normalmente:
l=2
c=1
INTERAÇÃO LUZ-MATÉRIA
Emissão
Reflexão
Transmissão
Absorção
Difração
Emissão
A emissão de luz ocorre por quatro mecanismos básicos:
• Emissão atômica ou molecular
• Emissão térmica
• Fluorescência e fosforescência
• Emissão estimulada
Emissão atômica ou molecular
É a emissão devida à transição de elétrons entre um estado
excitado e o estado fundamental.
Se caracteriza pela
emissão em raias
estreitas.
Raias de emissão
Do hidrogênio
Emissão térmica
Se dá pela dissipação da energia vibracional dos átomos
e/ou moléculas na forma de fótons.
É caracterizada
por um espectro
contínuo
dependente da
temperatura.
Fluorescência e fosforescência
Ocorre quando o retorno de um elétron do estado excitado
ao fundamental se dá em mais de um estágio, passando
por condições meta-estáveis.
•Fluorescência: tempos de até 10-6 s
•Fosforescência: tempos de até 10 s
Fluorescência
Fluorescência
Luz do
dia
Lâmpada
incandescente
Emissão estimulada
• Ocorre quando a passagem de um fóton perto de um
elétron excitado, induz a emissão de um fóton idêntico.
• Caracteriza-se por uma emissão monocromática,
paralela, polarizada e coerente (mesma fase)
• É o LASER (“Light Amplification by Stimulated Emission
of Radiation”)
Laser
Absorção
Da mesma forma que um eletron excitado emite um fóton
ao passar para o estado fundamental, um elétron no
estado fundamental pode absorver um fóton e passar
para um estado de maior energia.
Uma substância irá absorver luz na região do visível se
houverem transições eletrônicas possíveis com energias
envolvidas da grandeza da energia de um fóton de luz
visível.
Absorção
Normalmente as energias associadas às transições
eletrônicas em átomos ou moléculas simples são da ordem
de grandeza da energia de fótons de Raios-X.
Mas em moléculas ou cristais de estrutura eletrônica mais
complexa, estas transições podem ocorrem com energias
mais baixas, na região do visível.
Absorção
Teoria dos campos ligantes
4p*
4p
s*
4s*
eg*
4s
t2g
3d
s
eg
s
4p
4s
Fe+2
FeS2
S-2
Absorção
• Teoria das bandas de energia
Energia
Bandas de
condução
E
E
Bandas de
valência
Isolante
Semicondutor
Condutor
Objetos transparentes
A luz não sofre espalhamento ao atravessá-los mas é
parcialmente absorvida.
reflectância
especular
fonte
de luz
transmitância
regular
Objetos translúcidos
A luz sofre espalhamento e absorção parciais ao
atravessá-los
reflectância
difusa
transmitância
difusa
reflectância
especular
fonte
de luz
transmitância
regular
Objetos opacos
A luz não atravessa os objetos
reflectância difusa
fonte
de luz
reflectância
especular
(brilho)
Ótica Geométrica
• Refração
Lei de Snell:
sin b
sin a
=
n0
n1
Ótica Geométrica
• Reflexão regular
sen 2 (a - b )
R^ =
2
sen (a + b )
tan2 (a - b )
R|| =
tan2 (a + b )
Rreg
1  sen2 (a - b ) tan2 (a - b ) 
=  2
+

2
2  sen (a + b ) tan (a + b ) 
Ótica Geométrica
Polarização da luz refletida
1.0
Perpedicular
0.9
Paralela
0.8
Total
Reflexão
0.7
0.6
0.5
n0=1,00
n1=1,57
0.4
0.3
0.2
0.1
0.0
0
10
20
30
40
50
Angulo (graus)
60
70
80
90
Ótica Geométrica
• Reflexão total
n0
sena 0=
n1
• Incidência perpendicular
Rreg
 n1 - n0 

= 
 n1 + n0 
2
Treg
4n1n0
=
2
+
( n1 n0 )
Ótica Geométrica
Comportamento da luz refletida
1.0
Perpedicular
0.9
Paralela
0.8
Total
Reflexão
0.7
0.6
n0=1,57
n1=1,00
0.5
0.4
0.3
0.2
0.1
0.0
0
10
20
30
40
50
Angulo (graus)
60
70
80
90
Índices de refração
Índices de refração de alguns minerais:
Carbonato de cálcio (calcita)
1,486 - 1,658
Talco
1,54 – 1,60
Mica muscovita
1,55 – 1,61
Sulfato de bário
1,636 – 1,648
Óxido de magnésio
Caulim
Sílica (quartzo)
Dióxido de titânio (rutilo)
Dióxido de titânio (anatásio)
1,736
1,55 – 1,57
1,544 – 1,553
2,61 – 2,90
2,498 – 2,562
Sulfato de cálcio hidratado (gipsita)
1,52 – 1,55
Silicato de zircônio (zirconita)
1,96 – 2,01
Óxido de zircônio (badeleita)
2,13 – 2,20
Sílica hidratada (opala)
1,3 – 1,45
Hidróxido de alumínio
1,56 – 1,60
Índices de refração
Índices de refração de alguns polímeros:
Acetato de celulose (CA)
1,49
Butil acetato de celulose (CAB)
1,478
Policloreto de vinila (PVC)
1,54
Fluoreto de polivinilideno (PVDF)
1,42
Nylon 6 (PA6)
1,53
Policarbonato (PC)
1,585
Polietileno sulfonato (PES)
1,65
Polietileno de baixa densidade (LDPE)
1,51
Polietileno de alta densidade (HDPE)
1,54
Polietileno tereftalato (PET)
1,58 - 1,64
Polimetilmetacrilato (PMMA)
1,49
Polioximetileno (POM)
1,48
Poliestireno (PS)
Politetrafluoretileno (PTFE)
1,59 - 1,60
1,38
Índices de refração
Índices de refração de alguns líquidos:
Acetona
1,357
Tetracloreto de carbono
1,459
Etileno glicol
1,431
Etanol
1,359
Metanol
1,326
Metiletilcetona (MEK)
1,377
Polietileno glicol
1,460
Tolueno
1,493
Ciclohexano
1,424
Estireno
1,545
Água
1,335
Índices de refração
O índice de refração pode ser também representado por
um número complexo do tipo n-ik, onde k é o coeficiente de
absorção do material.
Para o óxido de cobre I:
l (nm)
n
k
300
2,00
1,85
350
2,40
1,44
400
2,80
0,99
450
3,06
0,60
500
3,12
0,35
550
3,10
0,19
600
3,02
0,13
650
2,90
0,10
700
2,83
0,083
Funcionamento da fibra ótica
O funcionamento da fibra ótica se
baseia no fenômeno da reflexão total:
Toda a luz que penetrar em uma
extremidade da fibra com um ângulo
menor que o limite de reflexão total vai
sendo refletida indefinidamente sem
ocorrer perda lateral de energia.
Ótica Geométrica
Iluminação difusa (Lei
de Lambert)
p
2
Rdif = 2  Rreg (a ). sena . cos a .da
0
Reflexão regular/difusa
• A diferença entre uma reflexão regular ou difusa está na
qualidade da superfície.
• A transição entre estes modos pode ser estimada pelo
critério de Rayleigh:
h=
l
8. cos q
Luz visível:
(380 a 780 nm)
h : altura das irregularidades
l : comprimento de onda
q : ângulo de incidência
q = 0o
q = 45o
h = 0,07 mm
q = ~90o
h = 4,0 mm
h = 0,10 mm
Reflexão regular x difusa
Uma superfíce perfeitamente difusora é um modelo ideal
que não é observado na prática. Superfícies reais misturam
reflexão especular com difusa.
Reflexão
especular
Luz
incidente
Amostra
Espalhamento de luz
O espalhamento da luz por partículas de matéria se dá pela
combinação de três fenômenos:
Reflexão
Refração
Difração
Espalhamento de luz
À combinação dos três fenômenos juntos chama-se
Difusão (ou espalhamento):
O espalhamento aumenta:
• Com o aumento da diferença entre
os índices de refração das
partículas e do meio
• Quando o tamanho das partículas
se aproxima do comprimento de
onda da luz
Espalhamento da luz
Existem vários modelos para descrever a difusão causada
por partículas individuais:

Mie
Rayleigh/Gans
1

0
Dimensão relativa
MEIOS TRANSPARENTES
Lei de Beer-Lambert
Lei de Beer-Lambert
Lei de Lambert (meios absorventes)
I = I0 .e
-
4pks
l0
Lei de Beer-Lambert (em função da concentração)
I = I0 .e
- e .c . d
1
A = ln  = e .c.d
T 
Lei de Beer-Lambert
• A lei de Beer-Lambert determina que a absorbância é
aditiva em relação à concentração, ou seja:
A =  e i .ci .d
i
MEIOS OPACOS
(DIFUSORES)
Modelo de Kubelka-Munk
Correção de Saunderson
Modelo de Kubelka-Munk
Pressupostos:
• Iluminação difusa (lei de Lambert)
• Tamanho das partículas muito menor que a espessura
do meio
• Partículas aleatoriamente distribuídas e
aproximadamente da mesma dimensão
• Inexistência de reflexão especular
Modelo de Kubelka-Munk
dI
= -( K + S ) I + SJ
dx
dJ
= -( K + S ) J + SI
dx
d
I
J
0
Rg
dx
Modelo de Kubelka-Munk
 1


S .d .
R 
 R



Rg - R
1
.e
- R  Rg R
R 

R=
 1


S .d .
R 


1
 R



( Rg R )  Rg
.e

R 

(1 - R )
K
=
F ( R ) 
2 R
S
2
Modelo de Kubelka-Munk
Permite uma relação entre a reflectância e a composição:
n
 K 
=


 S  mist

K ici

Sici
i =1
n
i =1
“Modelo de duas constantes”
Modelo de Kubelka-Munk
O coeficiente de difusão da mistura pode ser considerado
constante quando:
• Toda a difusão ocorre no substrato (têxteis, etc…)
• Um componente altamente difusor (branco) está presente
em largo excesso
Modelo de Kubelka-Munk
Neste caso:
F(R)
K
Ki
  =  ci =  K ici
 S  mist i =0 S 0
i =0
n
n
“Modelo
de uma constante”
K’
F0
c
Correção de Saunderson
Raio incidente
Substrato difusor
(Kubelka-Munk)
Modelamento
Raio incidente
k1
Interface
k2
Substrato difusor
(Kubelka-Munk)
Equacionamento
Rc = k1 + (1 - k1 )R (1 - k 2 )+ (1 - k1 )Rk 2 R (1 - k 2 )+ (1 - k1 )Rk 2 Rk 2 R (1 - k 2 )+ ...
[
]
Rc = k1 + (1 - k1 )(1 - k 2 )R 1 + k 2 R + (k 2 R )2 + (k 2 R )3 + ...

Como
x =
n
n =0
Temos: Rc = k1
1
1- x
(1 - k1 )(1 - k2 )R
+
1 - k2 R
para x<1
Rc - k1
ou R =
1 - k1 - k 2 (1 - Rc )
MEDIÇÃO
Colorímetros
Espectrocolorímetros
Geometrias de Medição
Colorímetro
Iluminação
X=20,82
Y=18,34
Z=36,53
Filtros
Amostra
Detectores
Espectrocolorímetro
Iluminação
Detectores
R400=05,42
R420=06,84
Amostra
.
.
.
.
Rede de
difração
R680=82,74
R700=83,12
Espectrocolorímetro
Espectrocolorímetro
Geometrias de Medição
8o
8o
0/45
detector
detector
detector
d/0
d/0
Especular
Incluso
Especular
Excluso
Geometria d/8