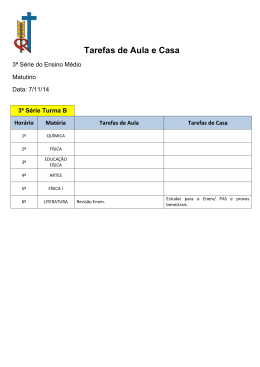
MATEMÁTICA - 3o ANO
MÓDULO 07
FUNÇÃO DO 1º GRAU
y
(0,c)
x
y
(2,2)
(0,0)
(1,1)
x
(-1,-1)
(-2,-2)
y
x
y
3
(1,3)
(0,1)
1
x
y
1
(1,1)
( ,0) 1
(0,1)
x
y
3
(1,3)
(0,1)
1
x
y
(0,3)
2
(1,2)
x
1
y
-1
y - f(x)
2
4
7
x
+
x
-
x=
x
f(x) tem o sinal de -a
f(x) tem o sinal de a
Como pode cair no enem
3.0
2.0
1.0
-1.0
-1.0
1.0
2.0
3.0
4.0
2.0
1.0
-1.0
-1.0
Número de jogos vendidos
-2.0
-2.0
-3.0
-3.0
d)
e)
6.0
4.0
3.0
2.0
1.0
-1.0
1.0
2.0
3.0
4.0
Número de jogos vendidos
2.0
3.0
4.0
Número de jogos vendidos
3.0
2.0
1.0
1.0
2.0
3.0
4.0
Número de jogos vendidos
3.0
1.0
1.0
4.0
-1.0
5.0
Lucro (em R$ 1.000,00
Lucro (em R$ 1.000,00
5.0
5.0
3.0
Lucro (em R$ 1.000,00
Lucro (em R$ 1.000,00
Lucro (em R$ 1.000,00
(ENEM) Uma empresa produz jogos pedagógicos para computadores, com custos fixos
de R$ 1.000,00 e custos variáveis de R$100,00 por unidade de jogo produzida. Desse
modo, o custo total para x jogos produzidos é dado por C(x) = 1 + 0,1x (em R$ 1.000,00).
A gerência da empresa determina que o preço de venda do produto seja de R$ 700,00. Com isso,
a receita bruta para x jogos produzidos é dada por R(x) = 0,7x (em R$ 1.000,00). O lucro líquido, obtido
pela venda de x unidades de jogos, é calculado pela diferença entre a receita bruta e os custos totais.
O gráfico que modela corretamente o lucro líquido dessa empresa, quando são produzidos x jogos é:
a)
b)
c)
6.0
4.0
4.0
Número de jogos vendidos
Fixação
s1) (ENEM) Uma indústria fabrica um único tipo de produto e sempre vende tudo o que produz.
O custo total para função, simbolizada por CT, enquanto o faturamento que a empresa obtém
.com a venda da quantidade q também é uma função, simbolizada por FT. O lucro total (LT)
obtido pela venda da quantidade q de produtos é dado pela expressão LT(q) = FT(q) - CT(q).
Considerando-se as funções FT(q) = 5q e CT(q) = 2q + 12 como faturamento e custo, qual
a quantidade mínima de produtos que a indústria terá de fabricar para não ter prejuízo?
:a) 0
b) 1
c) 3
d) 4
e) 5
Fixação
2) (ENEM) O saldo de contratações no mercado formal no setor varejista da região metropolitana de São Paulo registrou alta. Comparando as contratações deste setor no mês de fevereiro
com as de janeiro deste ano, houve incremento de 4 300 vagas no setor, totalizando 880 605
trabalhadores com carteira assinada.
(Disponível em: http://www.folha.uol.com.br. Acesso em: 26 abr. 2010 [adaptado].)
Suponha que o incremento de trabalhadores no setor varejista seja sempre o mesmo nos
seis primeiros meses do ano.
Considerando-se que y e x representam, respectivamente, as quantidades de trabalhadores
no setor varejista e os meses, janeiro sendo o primeiro, fevereiro, o segundo, e assim por diante,
a expressão algébrica que relaciona essas quantidades nesses meses é:
a) y = 4 300x
b) y = 884 905x
c) y = 872 005 + 4 300x
d) y = 876 305 + 4 300x
e) y = 880 605 + 4 300x
Fixação
-3) (ENEM) O gás natural veicular (GNV) pode substituir a gasolina ou álcool nos veículos automotores. Nas grandes cidades, essa possibilidade tem sido explorada, principalmente, pelos
táxis, que recuperam em um tempo relativamente curto o investimento feito com a conversão
por meio da economia proporcionada pelo uso do gás natural. Atualmente, a conversão para
gás natural do motor de um automóvel que utiliza a gasolina custa R$ 3.000,00. Um litro de
gasolina permite percorrer cerca de 10 km e custa R$ 2,20, enquanto um metro cúbico de GNV
permite percorrer cerca de 12 km e custa R$ 1,10. Desse modo, um taxista que percorre 6.000
km por mês recupera o investimento da conversão em aproximadamente:
a) 2 meses;
,b) 4 meses;
c) 6 meses;
d) 8 meses;
e) 10 meses.
Fixação
F
4) (ENEM) A figura a seguir representa o boleto de cobrança da mensalidade de uma escola.5
Referente ao mês de junho de 2009.
c
d
Se M (x) é o valor, em reais, da mensalidade a ser paga, em que x é o número de dias ema
atraso, então:
b
a) M (x) = 500+ 0,4x d) M (x) = 510 + 40x
c
b) M (x) = 500 +10x e) M (x) = 500 + 10,4x
d
c) M (x) = 510 + 0,4x
e
Fixação
5) (ENEM) O gráfico abaixo, obtido a partir de dados do Ministério do Meio Ambiente, mostra o crescimento do número de espécies da fauna brasileira ameaçadas de extinção, em 2011, seria igual a:
Se mantida, pelos próximos anos, a tendência de crescimento mostrada no gráfico, o número
de espécies ameaçadas de extinção será em 2011 igual a:
ma) 465
b) 493
c) 498
d) 538
e) 699
Fixação
F
6) (UERJ) A promoção de uma mercadoria em um supermercado está representada, no gráfico7
abaixo, por 6 pontos de uma mesma reta.
c
v
valor total de compra (R$)
e
150
m
u
e
50
5
20
30
quantidade de unidades
compradas
Quem comprar 20 unidades dessa mercadoria, na promoção, pagará por unidade, em reais,
o equivalente a:
a) 4,50c) 5,50
a
b) 5,00d) 6,00
b
Fixação
7) (UFRJ) Uma fábrica produz óleo de soja por encomenda, de modo que a produção é comercializada. O custo de produção é composto de duas parcelas. Uma parcela fixa, independente do
volume produzido, corresponde a gastos com aluguel, manutenção de equipamentos, salários
etc.; a outra parcela é variável, dependente da quantidade de óleo fabricado.
No gráfico a seguir, a reta r1 representa o custo de produção e a reta r2 descreve o faturamento da empresa, ambos em função do número de litros comercializados. A escala é tal que
uma unidade representa R$ 1.000,00 (mil reais) no eixo das ordenadas e 1000 (mil litros) no
eixo das abscissas.
r2
90
r1
40
10
60
a) Determine, em reais, o custo correspondente à parcela fixa.
b) Determine o volume mínimo de óleo a ser produzido para que a empresa não tenha prejuízo.
Proposto
1) (ENEM) O gráfico ao lado modela a distância percorrida, em km, por uma pessoa em certo
período de tempo. A escala de tempo a ser adotada para o eixo das abs-cissas depende da maneira como essa pessoa se desloca. Qual é a opção que apresenta a melhor associação entre
meio ou forma de locomoção e unidade de tempo quando são percorridos 10 km?
a) carroça – semana
b) carro – dia
c) caminhada – hora
d) bicicleta – minuto
e) avião – segundo
Proposto
o2) (UNIFICADO) Uma barra de ferro com temperatura inicial de -10°C foi aquecida até 30°C.
-O gráfico representa a variação da temperatura da barra em função do tempo gasto nessa
experiência. Calcule em quanto tempo, após o início da experiência, a temperatura da barra
atingiu 0°C.
Temperatura (ºC)
a) 1 min; b) 1 min 5 seg; c) 1 min 10 seg;
30
Tempo (minutos)
-10
5
d) 1 min 15 seg;
e) 1 min 20 seg.
Proposto
3) (ENEM)
VENDEDORES JOVENS
Fábrica de LONAS – Vendas no Atacado
10 vagas para estudantes, 18 a 20 anos, sem experiência. Salário: R$ 300,00 fixos + comissão de
R$ 0,50 por m2 vendido. Contato: 0xx97-43421167
ou [email protected]
Na seleção para as vagas deste anúncio, feita por telefone ou correio eletrônico, propunha-se
aos candidatos uma questão a ser resolvida na hora. Deveriam calcular seu salário no primeiro
mês, se vendessem 500 m de tecido com largura de 1,40 m, e no segundo mês, se vendessem
o dobro. Foram bem sucedidos os jovens que responderam, respectivamente,
a) R$ 300,00 e R$ 500,00
b) R$ 550,00 e R$ 850,00
c) R$ 650,00 e R$ 1000,00
d) R$ 650,00 e R$ 1300,00
e) R$ 950,00 e R$ 1900,00
Proposto
4) (UERJ) Leia o texto a seguir:
PCIA
cios observaram que a sombra
e
(Adaptado de Revista Galileu, janeiro de 2001)
Um estudante fez uma experiência semelhante à des-crita no texto, utilizando uma vareta OA de
2 metros de comprimento. No início do inverno, mediu o comprimento da sombra OB, encontrando
8 metros. Utilizou, para re-presentar sua experiência, um sistema de coordenadas cartesianas, no
qual o eixo das ordenadas (y) e o eixo das abscissas (x) continham, respectivamente, os segmentos
de reta que representavam a vareta e a sombra que ela determinava no chão.
Esse estudante pôde, assim, escrever a seguinte equação da reta que contém o segmento AB:
a) y = 8 – 4x
b) x = 6 – 3y
c) x = 8 – 4y
d) y = 6 – 3x
Proposto
5) (ENEM) Três empresas de táxi W, K e L estão fazendo promoções: a empresa W cobra R$
2,40 a cada quilômetro rodado e com um custo inicial de R$ 3,00; a empresa K cobra R$ 2,25
a cada quilômetro rodado e uma taxa inicial de R$ 3,80 e, por fim, a empresa L, que cobra R$
2,50 a cada quilômetro rodado e com uma taxa inicial de R$ 2,80. Um executivo está saindo
de casa e vai de táxi para uma reunião que é a 5 km do ponto de táxi, e sua esposa sairá do
hotel e irá para o aeroporto, que fica a 15 km do ponto de táxi.
Assim, os táxis que o executivo e sua esposa deverão pegar, respectivamente, para terem
a maior economia são das empresas:
a) W e L
b) W e K
c) K e L
d) K e W
e) K e K
Proposto
6) (UFRJ) Uma operadora de celular oferece dois planos no sistema pós-pago. No plano A,
5paga-se uma assinatura de R$ 50,00 e cada minuto em ligações locais custa R$ 0,25. No plano
B, paga-se um valor fixo de R$ 40,00 para até 50 minutos em ligações locais e, a partir de 50
ominutos, o custo de cada minuto em ligações locais é de R$ 1,50.
a) Calcule o valor da conta em cada plano para um consumo mensal de 30 minutos em ligações locais.
b) Determine a partir de quantos minutos, em ligações locais, o plano B deixa de ser mais
vantajoso do que o plano A.
Proposto
7) (ENEM) Uma empresa de telefonia fixa oferece dois planos aos seus clientes: no plano K,
o cliente paga R$ 29,90 por 200 minutos mensais e R$ 0,20 por cada minuto excedente; no
plano Z, paga R$ 49,90 por 300 minutos mensais e R$ 0,10 por cada minuto excedente.
a)
O gráfico que representa o valor pago, em reais, nos dois planos em função dos minutos utilizados é:
b)
c)
R$
R$
R$
89,90
89,90
Z
79,90
Z
79,90
79,90
69,90
69,90
59,90
59,90
59,90
49,90
49,90
49,90
39,90
39,90
69,90
K
29,90
0
d)
100 200 300 400 500
89,90
e)
59,90
49,90
49,90
39,90
39,90
29,90
min
0
100 200 300 400 500
Z
69,90
59,90
29,90
min
0
100 200 300 400 500
29,90
min
0
K
79,90
Z
69,90
100 200 300 400 500
R$
89,90
K
79,90
min
0
R$
K
39,90
29,90
min
Z
89,90
K
100 200 300 400 500
Proposto
,
8) (UFF) O gráfico da figura a seguir, formado por dois segmentos de reta, mostra o crescimento
da “esperança de vida” do brasileiro, de 1990 a 2004. Assim, pelo gráfico, pode-se observar
que a “esperança de vida” em 1990 era de 66 anos, em 2000 passou a ser de 70 anos e em
2004 passou a ser de 72 anos.
2004
(Adaptado de IBGE, Diretoria de Pesquisas, Coordenação de População e Indicadores Sociais)
a) Determine, com base no gráfico, a “esperança de vida” no ano de 1995.
b) Faça uma estimativa para a “esperança de vida” no ano de 2010, considerando que o gráfico no período 2000 a 2010 é o segmento de reta obtido pelo prolongamento do gráfico no
período 2000 a 2004.
Proposto
9) A tabela abaixo mostra a temperatura das águas do oceano Atlântico (no nível do Equador)
em função da profundidade:
Profundidade Superfície
100m
500m
Temperatura
21°C
7°C
27°C
1000m 3000m
4°C
2,8°C
Admitindo que a variação da temperatura seja, aproximadamente, linear entre cada duas das
medições feitas para a profundidade, a temperatura prevista para a profundidade de 400m é de:
a) 16°C
b) 14°C
c) 12°C
d) 10,5°C
e) 8°C
Proposto
10) (UFRJ) A cada usuário de energia elétrica é cobrada uma taxa mensal de acordo com o
seu consumo no período, desde que esse consumo ultrapasse um determinado nível. Caso
contrário, o consumidor deve pagar uma taxa mínima referente a custos de manutenção. Em
certo mês, o gráfico consumo (em kWh) X preço (em R$) foi apresentado a seguir:
R$
2250
1750
1250
750
250
50
100
150
200
KWh
a) Determine entre que valores de consumo em kWh é cobrada a taxa mínima.
b) Determine o consumo correspondente à taxa de R$ 1.950,00.
Proposto
11) (UERJ) Ainda que a grande disparidade de renda no Brasil tenha razões históricas, econômicas e políticas que ultrapassam a ação do Parlamento, não deixa de ser agressiva a crueza
com que senadores aprovam um salário mínimo de R$ 65,00 para o país e um rendimento de
R$ 12 mil para si mesmos.
(Jornal Folha de S.Paulo - 15/10/94)
Digitando-se uma máquina calculadora, nesta ordem: I) o valor da proposta do salário de
Senador;
II) o sinal de menos;
III) o valor do salário mínimo;
IV) o sinal de igual.
Cada vez que se repete a operação do 4o item, a máquina subtrai do número que aparece
no visor um salário mínimo. O número de vezes que deve ser digitado o sinal de igual até se
obter um número negativo pela primeira vez é igual a:
a) 183
d) 186
b) 184
e) 187
c) 185
Proposto
-12) (CEFET) Newton quer imprimir folhetos com a propaganda de sua empresa. Na gráfica
A, o custo para a montagem deste folheto é de R$ 120,00 e o valor da impressão por unidade é R$ 0,20. A gráfica B cobra R$ 80,00 para a montagem e R$ 0,25 para impressão
de cada unidade. Após análise cuidadosa, Newton concluiu que:
a) é vantagem fazer a encomenda na gráfica B para qualquer quantidade de folhetos;
b) a gráfica A oferece um custo menor que a B para um número de folhetos menor que 800;
c) se encomendar 1.000 folhetos da gráfica B, irá gas-tar R$ 320,00;
d) se desejar 1.000 folhetos gastará menos se encomendar da empresa A;
e) para a quantidade de 800 folhetos, o custo de qualquer das empresas é igual a R$ 290,00.
Proposto
13) (UERJ) As baterias B1 e B2 de dois aparelhos celulares apresentam em determinado instante,
respectivamente, 100% e 90% da carga total. Considere as seguintes informações:
• as baterias descarregam linearmente ao longo do tempo;
•para descarregar por completo, B1 leva t horas e B2;
• no instante z, as duas baterias possuem o mesmo percentual de carga igual a 75%.
Observe o gráfico abaixo e responda:
y (% de carga)
100
90
75
0
O valor de t, em horas, equivale a:
a) 1
c) 3
b) 2
d) 4
z
t
(t + 2)
Proposto
,14) (UERJ) A função que descreve a dependência temporal da posição S de um ponto
material é representada pelo gráfico a seguir.
(RAMALHO JÚNIOR, Francisco. Os Fundamentos da Física. São Paulo: Moderna, 1993.)
Sabendo que a equação geral do movimento é do tipo S = A + Bt + Ct², os valores numéricos
das constantes A, B e C são, respectivamente:
a) 0, 12, 4
b) 0, 12, - 4
c) 12, 4, 0
d) 12, - 4 , 0
Proposto
15) (UERJ) O gráfico abaixo representa, em bilhões de dólares, a queda das reservas internacionais de um determinado país no período de julho de 2000 a abril de 2002.
(Adaptado de Veja, 01/05/2002)
Admita que, nos dois intervalos do período conside- rado, a queda de reservas tenha sido
linear.
Determine o total de reservas desse país, em bilhões de dólares, em maio de 2001.
Proposto
-16) (UERJ) Em uma partida, Vasco e Flamengo levaram ao Maracanã 90.000 torcedores.
Três portões foram abertos às 12 horas e até às 15 horas entrou um número constante de
pessoas por minuto. A partir desse horário, abriram-se mais 3 portões e o fluxo constante
de pessoas aumentou.
Os pontos que definem o número de pessoas dentro do estádio em função do horário de
entrada estão contidos no gráfico a seguir:
o
o
Quando o número de torcedores atingiu 45.000, o relógio estava marcando 15 horas e:
a) 20 min
b) 30 min
c) 40 min
d) 50 min
Proposto
P
1
17) (ENEM) O gráfico mostra o número de favelas no município do Rio de Janeiro entre 1980u
d
e 2004, considerando que a variação nesse número entre os anos considerados é linear.
750
a
573
372
b
1980
1992
2004
Se o padrão na variação do período 2004/2010 se mantiver nos próximos 6 anos, e sabendo
que o número de favelas em 2010 é 968, então o número de favelas em 2016 será
a) menor que 1.150
c
b) 218 unidades maior que em 2004
c) maior que 1.150 e menor que 1.200
d) 177 unidades maior que em 2010
e) maior que 1.200
Proposto
c)
2000
2000
1750
1750
1500
1500
1250
1250
1000
1000
750
750
500
500
250
0
250
0
5
50
75
100
125
150
175
200
225
Produtos vendidos
Salário em R$
2250
e)
02
5
50
75
100
125
150
175
200
225
02
5
50
75
100
125
150
175
200
225
Produtos vendidos
2250
Salário em R$
02
2000
2000
1750
1750
1500
1500
1250
1250
1000
1000
750
750
500
500
250
0
250
0
02
5
50
75
100
125
150
175
200
225
02
5
50
75
100
125
150
175
200
225
Produtos vendidos
2250
Salário em R$
b)
Salário em R$
18) Certo vendedor tem seu salário mensal calculado da seguinte maneira: ele ganha um valor fixo de R$ 750,00, mais
uma comissão de R$ 3,00 para cada produto vendido. Caso ele venda mais de 100 produtos, sua comissão passa a ser
de R$ 9,00 para cada produto vendido, a partir do 101º produto vendido.
a) 2250
d) 2250
2000
1750
1500
1250
1000
750
500
250
0
Produtos vendidos
Produtos vendidos
Proposto
19) (ENEM) As curvas de oferta e de demanda de um produto representam, respectivamente,
as quantidades que vendedores e consumidores estão dispostos a comercializar em função do
preço do produto. Em alguns casos, essas curvas podem ser representadas por retas. Suponha
que as quantidades de oferta e de demanda de um produto sejam, respectivamente, representadas pelas equações:
QO= -20 + 4P
QD= 46 - 2P
em que QO é quantidade de oferta, QD é a quantidade de demanda e P é o preço do produto.
A partir dessas equações, de oferta e de demanda, os economistas encontram o preço de
equílibrio de mercado, ou seja, quando o QO e QD se igualam. Para a situação descrita, qual o
valor do preço de equilíbrio?
a) 5
d) 23
b) 11
e) 33
c) 13