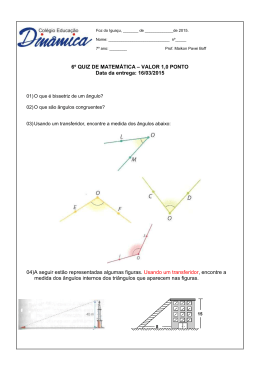
A
L AL
AUU
39
A
39
Medida de ângulos
H
á muitas situações em que uma pequena
mudança de ângulo causa grandes modificações no resultado final. Veja alguns
casos nos quais a precisão dos ângulos é fundamental:
E
N
N
O
N
E
O
E
S
S
SO
Para saber
a direção a seguir
Para instalar uma
antena parabólica
Na construção civil
No futebol
Na localização no mapa
Na arquitetura
Introdução
A U L A
39
São tantos os exemplos que você já deve estar se lembrando de outros.
Mas o que é ângulo?
Ângulo é o nome que se dá à
abertura formada por duas
semi-retas que partem de
um mesmo ponto.
lado
‰ngulo
v•rtice
lado
As semi-retas que formam o ângulo são os lados do ângulo, e o ponto de
origem das semi-retas é chamado vértice do ângulo.
Nesta aula vamos estudar um pouco mais sobre os ângulos, como medi-los
(que instrumentos usar e qual a unidade de medida) e alguns exemplos e
aplicações importantes.
O ângulo mais famoso, justamente por ser o mais comum, é o ângulo reto.
Você se lembra dele? O ângulo reto é aquele ângulo formado por duas retas
perpendiculares e que está sempre presente nos esquadros. Você deve lembrar
também que o ângulo reto mede 90º.
Falando em medida de um ângulo, neste caso o ângulo reto, perguntamos:
Como medir um ângulo?
O instrumento utilizado para medir ângulos é o transferidor, e você pode
encontrá-lo de dois tipos:
350 0 10 20
40
190 180 170 160 30
03
33 200
15
0 210
0 1 40
2
3 20
40 45
2
0 180 190
2
0
60 17
10 0 350 34 0 21
01
03 0
15 20
30 22
30
32 0
0
0 180
60 17
10 0
01
15 20
30
0 10
2
180 170 1 0 3
0
60
15
0 1 40
40 45
0
14
0
14
0
45 4
100
80
70 100 90 80 110 1
2
70
60 110
60 0 13
0
50 0 12
50 0
13
0
45 4
100
80
70 100 90 80 110 1
2
70
60 110
60 0 13
0
50 0 12
50 0
13
260 270 280
50 280 270 260 290 3
250 00
02
24 290
24 3
0 00
0 2 10
23 10 3
30
3
Nossa aula
Usar o transferidor é muito simples. Observe estes exemplos e depois
pratique desenhando ângulos e medindo-os com seu transferidor.
Dado um ângulo, devemos fazer coincidir seu vértice com o centro do
transferidor e um de seus lados com a marca do zero do transferidor, como
mostram as figuras:
0 10
2
180 170 1 0 3
0
60
15
0 1 40
40 45
0 180
60 17
10 0
01
15 20
30
0 180
60 17
10 0
01
15 20
30
0 10
2
180 170 1 0 3
0
60
15
0 1 40
40 45
0
14
40
1 0
45 4
100
80
70 100 90 80 110 1
2
70
60 110
60 0 13
0
50 0 12
50 0
3
1
0
45 4
100
80
70 100 90 80 110 1
2
70
60 110
60 0 13
0
50 0 12
50 0
3
1
centro
centro
marca de 60º
marca de 90º
A unidade de medida de ângulo é o grau. Desenhando uma circunferência
e dividindo-a em 360 pequenos ângulos iguais, obtemos um ângulo de um grau.
Usando o transferidor, desenhamos um ângulo de 1º (um grau). Verifique como
ele é pequeno!
1
EXEMPLO 1
Qual destes ângulos é maior?
Usando um transferidor, você pode verificar que os três ângulos possuem
a mesma abertura (20 graus) e portanto são do mesmo tamanho.
Se dois ângulos têm a mesma abertura, também têm a mesma medida.
EXEMPLO 2
Na ilustração que está na próxima página, você pode observar uma parte do
litoral brasileiro. Vamos ver como calcular a direção, da rota de um avião,
supondo que ele viaje usando sempre a menor distância entre dois pontos, ou
seja, em linha reta.
Nos mapas usados pela aviação, encontramos pequenas bússolas
desenhadas sobre algumas cidades. Para calcular o ângulo de uma rota, o
piloto coloca um transferidor sobre o mapa e faz a leitura do ângulo.
O diâmetro do transferidor deve ter a mesma direção que a direção NorteSul da bússola, sendo que 0º corresponde ao norte magnético.
A U L A
39
Jo‹o Pessoa
Aracajœ
20 30 4045 50
10
0 150 140 13 60
0 170 16
01
20 70
0
18
11
0
Oceano Atl‰ntico
80 0
10
Rio de
Janeiro
L
S
110 120 130
100 0 60 50 45140 1
4
5
0
0 7
30 0 16
90 8
20 0
N
O
Classificando ângulos
Você já sabe que o ângulo que mede 90º é chamado ângulo reto. Outro
ângulo que recebe nome especial é o ângulo que mede 180º. Neste tipo de ângulo,
as duas semi-retas que formam os lados estão sobre uma mesma reta, e ele é
chamado ângulo raso.
0 180
60 17
10 0
01
15 20
30
180
40
0 10
2
180 170 1 0 3
0
60
15
0 1 40
40 45
100
80
70 100 90 80 110 1
2
70
60 110
60 0 13
0
2
0
1
5 0
50 0
13
1 0
45 4
0 180
60 17
10 0
01
15 20
30
90
40
1 0
45 4
100
80
70 100 90 80 110 1
2
70
60 110
60 0 13
0
2
0
1
5 0
50 0
13
0 10
2
180 170 1 0 3
0
60
15
0 1 40
40 45
39
Nesta ilustração, você pode conferir que a rota de um vôo do Rio de
Janeiro a Aracaju é de 56º. Observe que a rota do Rio de Janeiro a João
Pessoa também é de 56º, porém a distância desta viagem é maior do que
a da primeira.
0
18
0 0
17 0
1
A U L A
Ângulos com medidas entre 0º e 90º são chamados ângulos agudos, e
ângulos com medidas entre 90º e 180º são chamados ângulos obtusos.
‰ngulo obtuso
0 180
60 17
10 0
01
15 20
30
0 10
2
180 170 1 0 3
0
60
15
0 1 40
40 45
0
14
0
45 4
100
80
70 100 90 80 110 1
2
70
60 110
60 0 13
0
2
50 0 1
50 0
13
137
48
‰ngulo agudo
Na figura anterior, temos um ângulo agudo e um ângulo obtuso e, além
disso, a soma de suas medidas é igual a 180º. Quando a soma de dois ângulos
é 180º, eles são chamados ângulos suplementares.
Quando dois ângulos agudos somam 90º, eles são chamados ângulos
complementares.
‰ngulo
agudo
0 10
2
180 170 1 0 3
0
60
15
0 1 40
40 45
0 180
60 17
10 0
01
15 20
30
60
30
40
1 0
45 4
100
80
70 100 90 80 110 1
2
70
60 110
60 0 13
0
50 0 12
50 0
3
1
‰ngulo
agudo
Curiosidade
Você já observou um par de esquadros? Existem dois tipos de esquadro.
Um deles é formado por um ângulo reto e dois ângulos de 45º, e o outro
possui um ângulo reto, um ângulo de 30º e outro de 60º. Confira!
60
45
45
30
A U L A
39
A U L A
39
EXEMPLO 3
Para decidir com um carpinteiro qual o ângulo de inclinação que seu telhado
terá, você precisa saber que tipo de telha irá utilizar.
Um carpinteiro nos informou que, para usar telhas francesas, o telhado pode
ter um caimento de 45%. Isso significa que, nesse caso, para cada metro
horizontal, o telhado “cai” 45% de metro. Representamos essa situação com
um desenho em escala a seguir:
escala:
1 m = 10 cm
0,45
4,5 m
x
1m
Medindo com o transferidor o ângulo x de inclinação do telhado, encontramos 25º.
Se você decidir usar telha de amianto, o ângulo de inclinação pode ser um
ângulo de 10º. Nesse caso, o caimento do telhado seria aproximadamente de
15%. Confira usando o desenho a seguir.
escala:
1 m = 10 cm
0,15
m
1,5 m
x
1m
EXEMPLO 4
Você já reparou que, quando observamos um automóvel que se distancia ao
longo de uma grande avenida, ele parece estar diminuindo de tamanho? Ou
que, quando assistimos a um grande show, quanto mais longe do palco,
menores parecem ser os artistas?
5
20
Observe a ilustração abaixo. Nela, um homem foi desenhado maior do que
o outro para dar a impressão de que está mais perto de nós. Como vemos o
homem “menor” sob um ângulo de visão menor, nosso cérebro interpreta
a cena como se esse homem estivesse mais afastado do que o primeiro.
Podemos concluir que o ângulo de visão que temos de um objeto depende
da distância desse objeto e da posição que estamos em relação a ele. E nosso
ângulo de visão máximo, sem mexer a cabeça, é de 180º.
Os ângulos e a semelhança
Na Aula 21, você estudou semelhança de figuras planas. Relembre agora o
importante papel que os ângulos exercem no caso de figuras semelhantes.
Sempre que dois polígonos são semelhantes, seus ângulos são
iguais e seus lados são proporcionais e vice-versa.
Observe os polígonos abaixo.
Como são polígonos semelhantes, você pode medir os ângulos correspondentes em cada par e verificar que suas medidas são iguais.
A U L A
39
A U L A
39
Mas será que a recíproca é verdadeira? Ou seja, será que, sempre que os
ângulos forem iguais, os polígonos serão semelhantes?
Não! Basta verificar que isso não vale para um exemplo. Veja:
Um quadrado e um retângulo não são semelhantes.
No entanto, ambas as figuras possuem quatro ângulos retos.
Mas existe um caso especial. Quando o nosso polígono for
um triângulo é verdadeiro afirmar que se os três ângulos
correspondentes de dois triângulos são iguais, então os
triângulos são semelhantes.
Podemos verificar este fato construindo pares de triângulos com ângulos iguais. Observe o exemplo seguinte.
EXEMPLO 5
Construa dois triângulos diferentes com ângulos medindo 50º, 60º e 70º.
C
50
2 cm
A
A
2 cm
50
B
A
60
2 cm
B
Vamos construir o primeiro triângulo e chamá-lo de ABC. Desenhamos um
segmento qualquer que será sua base AB. Usando o transferidor, marcamos
em A um ângulo de 50º e em B um ângulo de 60º. Traçando as semi-retas que
formam o segundo lado de cada um desses ângulos, o ponto onde elas se
encontram é o vértice C do triângulo ABC.
Verifique que o ângulo com vértice em C mede 70º.
(50º + 60º + 70º = 180º)
A soma dos ângulos internos de um triângulo é igual a 180º.
Vamos agora utilizar o mesmo processo para desenhar outro triângulo MNP
com ângulos de 50º, 60º e 70º. Já que queremos um triângulo diferente,
vamos começar com uma base maior.
P
70
50
50
M
4 cm
N
M
60
4 cm
N
Agora, medindo os lados dos dois triângulos podemos verificar que são
proporcionais. Dobramos o comprimento da base, e os outros 2 lados, automaticamente, dobraram suas medidas.
Exercícios
A U L A
Exercício 1
Use o transferidor e meça os ângulos abaixo:
a)
b)
c)
39
Exercício 2
Desenhe ângulos conforme o que se pede:
a) agudo
b) reto
c) obtuso
d) raso
Exercício 3
Utilize o mapa do Exemplo 2 e determine os ângulos das rotas abaixo:
a) Rio-Vitória;
b) Rio-São Paulo
Exercício 4
No mesmo mapa, podemos observar que a rota Rio-Belém é de 15º. Se o
piloto errar e marcar nos aparelhos uma rota de 150º, o que acontece?
Exercício 5
Observe a bússola da figura e descubra, usando um transferidor, a quantos
graus correspondem as direções NE (Nordeste), SE (Sudeste), NW (Noroeste), SW (Sudoeste).
E
N
N
O
N
E
O
SE
S
SO
Exercício 6
Construa um triângulo MNP semelhante a qualquer triângulo cujos ângulos
meçam 110º, 30º e 40º.
Exercício 7
Determine o ângulo suplementar (ou o suplemento) de:
a 120º
b) 43º
Exercício 8
Determine o ângulo complementar (ou o complemento) de:
a) 37º
b) 25º
Estas
abreviaturas no
texto referem-se à
bússola, que
sempre traz as
direções em inglês.