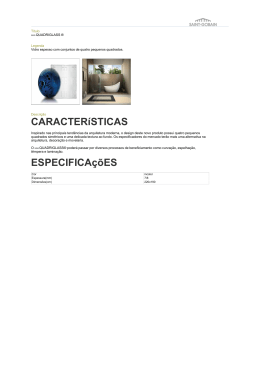
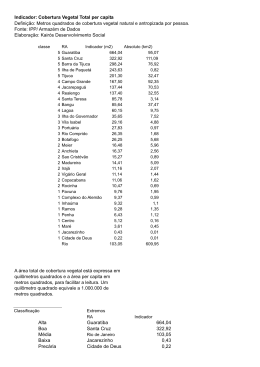
ISSN 1984-8218
O Método dos Mínimos Quadrados Utilizando a Fatoração LU
Patrícia D. B. Silva Camila G. Costa* Carlos A. Cavallini**
Fábio H. Oki Livia Matos Garcia**
Reginaldo Merejolli** Vanessa A. B. Pirani
Depto de Matemática, Estatística e Computação, FCT, UNESP
19060-900, Presidente Prudente, SP
E-mail: [email protected], [email protected], [email protected],
[email protected], [email protected], [email protected], [email protected]
RESUMO
O Método dos Mínimos Quadrados (MMQ) é uma técnica de otimização matemática
que tenta encontrar o melhor ajustamento para um conjunto de dados, minimizando a soma dos
quadrados das diferenças entre os valores observados e o valor estimado. Este método será
utilizado implicitamente para resolver um dado problema, utilizando a matriz de Vandermonde
e a Fatoração LU.
Para a aplicação é utilizado o software MATLAB.
O Método dos Mínimos Quadrados consiste em estimar variáveis estocásticas e seus
parâmetros de distribuição, a partir de amostras observadas com certa precisão. Três espaços
estão envolvidos nos problemas de ajustamento: o espaço das observações ou medidas, o espaço
do modelo matemático e o espaço dos parâmetros ou incógnitas.
À medida que a complexidade da realidade física que se pretende representar cresce, o
número de parâmetros mínimo necessário também aumenta. Num sistema de equações lineares
redundantes e inconsistentes, as soluções que obtemos para o conjunto (número mínimo) e
parâmetros a partir de diferentes subsistemas (formados com o mínimo de equações necessárias
para dar solução única) seriam distintas. Daí a necessidade do Método dos Mínimos Quadrados.
Um método de eliminação pode ser usado economicamente quando precisamos resolver
vários sistemas com a mesma matriz dos coeficientes. Mas, em algumas situações práticas, os
diversos termos independentes b no sistema Ax=b não estão disponíveis simultaneamente ou
podem depender da própria solução do sistema associada a outro b.
Através da decomposição LU, podemos decompor a matriz A no produto de uma matriz
triangular inferior por uma matriz triangular superior. Assim, o sistema Ax=b tem sua solução
encontrada através de dois novos sistemas: Ly=b e Ux=y.
Para a implementação do método, considere o conjunto de dados da tabela abaixo em
que um fabricante de placas de asfalto está interessado na relação entre as vendas em
determinado ano e fatores que influenciam as vendas.
Tabela 1: Relaciona os dados das marcas concorrentes com as vendas (por milhares) e do
potencial com as vendas (por milhares)
Segue abaixo as ilustrações do problema. Na Figura 1 estudamos a relação entre as
marcas concorrentes e as vendas por milhares, que se encontram nas duas primeiras colunas da
Tabela1, e na Figura 2 estudamos a relação entre o potencial e as vendas por milhares, que se
encontram nas duas últimas colunas da Tabela1.
*Bolsista de Mestrado FAPESP
**Bolsista de Mestrado CAPES
319
ISSN 1984-8218
Figura 1
Figura 2
Podemos concluir que o Método dos Mínimos Quadrados utilizando a Decomposição
LU é eficiente no ajuste de um polinômio de grau m para um conjunto de dados, e a utilização
da decomposição facilita a resolução do método, além de possibilitar a resolução do sistema
Ax=b para uma matriz A singular.
Palavras-chave: Álgebra Linear, Mínimos Quadrados, Fatoração LU.
Referências
[1] M. C. C. Cunha, Métodos Numéricos. Editora da Unicamp – Campinas-SP, 2000.
[2] Q. Dalmolin, Ajustamento por Mínimos Quadrados. Curitiba-PR, 2002.
[3] D. Hanselman, B. Littlefield: MATLAB 6: Um curso Completo. P. H., 2003.
320