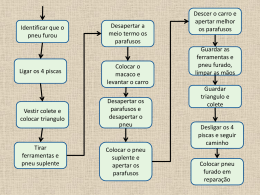
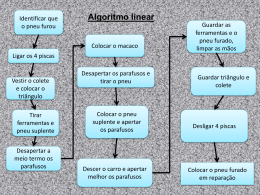
Introdução aos Algoritmos
Quando temos que fazer uma determinada tarefa e não sabemos muito bem
como fazê-la, podemos fazer perguntas para nos esclarecer a respeito do que
deve ser feito e como deve ser feito. Isso porque temos inteligência e habilidade
racional. Ao contrário de nós, o computador não tem senso próprio, portanto ele
deve receber instruções explícitas a respeito do que ele deve fazer. Se quisermos
que o computador resolva algum problema, desde o mais simples ao mais
complexo, devemos instruí-lo para fazer tal tarefa.
Os problemas, por mais simples que possam parecer, quando visualizados sob o
aspecto computacional, ficam um tanto mais complexos. Em razão disso, quando
temos um problema para o computador resolver, devemos conhecer bem esse
problema e pensar em todas as variáveis e dados que interferem no problema.
Em seguida, devemos dividir o problema em partes mais simples e lógicas.
Antes de passar as instruções do problema ao computador, podemos detalhar o
problema no papel para obtermos uma solução correta e otimizada. Uma maneira
de fazer isso é elaborar um algoritmo. Algoritmo é uma seqüência de passos que
visa atingir um objetivo bem definido.
Os algoritmos são muito freqüentes em nosso dia-a-dia, por exemplo: receita para
cozinhar algum prato; instruções para preenchimento dos formulários para fazer o
passaporte; instruções de como se faz ligação local, a cobrar e internacional; e
muitos outros.
Como já foi descrito, as instruções (também denominadas de comandos) que
compõem um algoritmo, devem ser claras, coerentes e lógicas. Se não forem
assim, e dependendo de quem as executa, podem ocorrer problemas que
impeçam chegar ao resultado final.
Um algoritmo correto deve possuir 3 qualidades:
z
z
z
cada passo do algoritmo deve ser uma instrução que possa ser realizada;
a ordem dos passos deve ser precisamente determinada; e,
o algoritmo deve ter fim.
Um exemplo
Vamos fazer um algoritmo para trocar o pneu de um carro e representá-lo através
de um diagrama. Inicialmente vamos pensar em uma solução bem geral, como a
da figura abaixo. Quem for executar esse algoritmo basta começar do início e ir
seguindo as setas até chegar ao fim. O algoritmo representado na figura abaixo é
bem simples, contém apenas a instrução trocar o pneu.
Mas vamos pensar na possibilidade do estepe estar vazio. Isso requer uma
decisão entre dois casos: quando o estepe está vazio ou quando o estepe não
está vazio. Antes de trocarmos o pneu, podemos averiguar se o estepe está vazio
ou não. A figura abaixo mostra o nosso algoritmo modificado para fazer essa
verificação. Repare que há dois caminhos a seguir partindo do losango vermelho.
Se o estepe estiver vazio, deve-se seguir para o caminho da esquerda e executar
a instrução chamar o borracheiro e ir para o fim do algoritmo. Se o estepe não
estiver vazio, deve-se seguir para o caminho da direita e executar a instrução
mudar o pneu e ir para o fim do algoritmo.
A instrução mudar o pneu pode ser detalhada em várias outras ações que estão
envolvidas quando vamos mudar o pneu. Por exemplo, antes de mudar o pneu
temos que levantar o carro, desparafusar o pneu, etc. A figura abaixo mostra o
nosso algoritmo modificado para incluir essas ações. Quando o algoritmo é
executado, começando do início, seguimos até o losango e se o estepe não
estiver vazio, seguimos para a direita e vamos executar as instruções nessa
ordem:
z
z
z
z
z
z
levantar o carro
desparafusar o pneu
remover o pneu
colocar o estepe
parafusar o estepe
abaixar o carro
Por último, seguimos para o fim. Caso o estepe esteja vazio, seguimos o caminho
da esquerda e somente será executada a instrução chamar o borracheiro,
seguindo depois para o fim do algoritmo.
Observe a instrução desparafusar o pneu, ela ainda pode ser detalhada nas
instruções:
z
z
z
z
desapertar o primeiro parafuso
desapertar o segundo parafuso
desapertar o terceiro parafuso
desapertar o quarto parafuso
O mesmo acontece com a instrução parafusar estepe, que pode ser detalhada
em:
z
z
z
z
apertar o primeiro parafuso
apertar o segundo parafuso
apertar o terceiro parafuso
apertar o quarto parafuso
Mas essas repetições são muito incovenientes, imagine se existissem 20
parafusos! Para solucionar esse problema podemos utilizar uma estrutura de
repetição. A figura abaixo mostra o nosso algoritmo modificado para incorporar
essa estrutura. Quando o algoritmo é executado, começando do início e seguindo
para o losango, se o estepe não estiver vazio, segue-se o caminho da direita e a
instrução levantar o carro será executada. A seguir vem a estrutura de repetição
e enquanto houver parafuso para desapertar a instrução desapertar parafuso
será executada. À cada vez que a instrução desapertar parafuso é executada, o
controle do algoritmo volta para verificar se existe parafuso para desapertar. Caso
ainda tenha parafuso para desapertar, novamente a instrução desapertar
parafuso será executada, caso não tenha parafuso para desapertar a próxima
instrução a ser executada é remover o pneu e logo em seguida colocar estepe.
Nesse ponto, seguindo a seta, há novamente uma estrutura de repetição e a
instrução apertar parafuso será executada enquanto houver parafuso para
apertar. Neste caso essa instrução será executada 4 vezes, porque são 4
parafusos. A seguir a instrução abaixar o carro será executada, e por último,
seguindo a seta, chega-se ao fim do algoritmo.
Agora sim, temos um algoritmo completo para trocar o pneu de um carro. Para
chegar a esse algoritmo começamos de uma solução bem geral do problema e
prosseguimos até o algoritmo final, sempre aumentando o nível de detalhamento.
Mas, será que esse nível de detalhe que chegamos é suficiente? A resposta a
essa pergunta é que depende de quem vai executar esse algoritmo. Se for uma
pessoa, certamente ela conseguirá trocar o pneu seguindo esses passos. Mas se
for, por exemplo, um robô? Dificilmente um robô conseguirá trocar o pneu
seguindo os passos do nosso algoritmo.
Os nossos algoritmos serão escritos em linguagem algorítmica. Essa linguagem
será formalizada nas próximas aulas, por agora, vamos transformar o nosso
algoritmo de trocar pneu, representado por um diagrama anteriormente, na língua
portuguesa mesmo.
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
| início
|
se o estepe estiver vazio então
|
chamar o borracheiro
|
senão
|
levantar o carro
|
enquanto houver parafuso para desapertar faça
|
desapertar parafuso
|
fim do enquanto
|
remover pneu
|
colocar estepe
|
enquanto houver parafuso para apertar faça
|
apertar parafuso
|
fim do enquanto
|
abaixar carro
|
fim do se
| fim
O algoritmo acima funciona da mesma maneira descrita anteriormente. Os
números no início de cada linha do algoritmo é somente para ficar mais fácil de
comentá-lo aqui nesse texto. O algoritmo começa na linha 01, mas como só
existe a palavra início para indicar o início do algoritmo nada é executado. Na
linha 02 há uma decisão a ser tomada. Se o estepe estiver vazio, então a
instrução chamar o borracheiro, que está na linha 03, será executada. Mas, se o
estepe não estiver vazio, então a instrução levantar o carro, que está na linha
05, será executada. Em seguida passa-se para a próxima instrução na linha 06.
Enquanto houver parafuso para desapertar a instrução da linha 07 desapertar
parafuso será executada. Nesse caso, ela será executada 4 vezes por causa dos
4 parafusos do pneu. Quando não houver mais parafuso para desapertar, passase para a linha 09 e a instrução remover pneu será executada. Em seguida, a
instrução da linha 10, colocar estepe, será executada. Na linha 11 há uma
estrutura de repetição e enquanto houver parafuso para apertar, a instrução
apertar parafuso, da linha 12, será executada. Essa instrução também será
executada 4 vezes. Quando não houver mais parafuso para apertar, passa-se à
linha 14 e a instrução abaixar o carro será executada. Na linha 15 nada será
executado, fim do se, é só para indicar o final da estrutura condicional. Por
último, na linha 16, o algoritmo termina.
Exercícios
z
z
Faça um algoritmo para fazer pipoca.
Faça um algoritmo para fazer uma ligação telefônica.