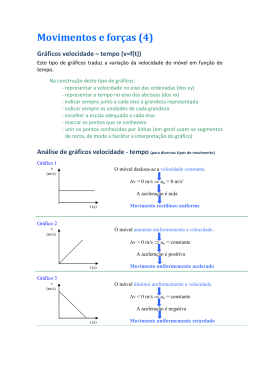
Tipos de movimento
A primeira coisa que deve estar bem compreendida são os tipos de movimento.
Quando a resultante das forças que atuam sobre um corpo é nula, o seu movimento será retilíneo, uniformem
(m.r.u.) ou repouso.
Quando a resultante das forças que atuam sobre um corpo é constante, o seu movimento será retilíneo,
uniformemente variado (m.r.u.v.).
Por sua vez, este pode ser:


Uniformemente acelerado (m.r.u.a.). se os sentidos da velocidade e da força forem iguais.
Uniformemente retardado (m.r.u.r.), se os sentidos da velocidade e da força forem diferentes.
A equação das posições destes tipos de movimento tem a forma
𝒚 = 𝒚𝟎 + 𝒗𝟎 𝒕 +
𝟏 𝟐
𝒂𝒕
𝟐
E a lei das velocidades é dada por
𝒗 = 𝒗𝟎 + 𝒂𝒕
Projétil vertical
Na situação do projétil, a única força qua atua sobre o corpo será o seu peso, vertical, de cima para
baixo, e com valor constante, pelo que o seu movimento será do tipo m.r.u.v, (sendo a sua
aceleração a aceleração gravítica g.)
P
Durante subida, os sentidos da velocidade e da força são
contrários, sendo m.r.u.r.
Durante descida, os sentidos da velocidade e da força são iguais, sendo
m.r.u.a.
A lei das posições será sempre
𝒚 = 𝒚𝟎 + 𝒗𝟎 𝒕 +
𝟏 𝟐
𝒈𝒕
𝟐
O que faz mudar o sinal são os sentidos dos vetores das grandezas
vetoriais da fórmula. Devemos ter em conta o sinal da velocidade inicial
(v0) e da aceleração, que no caso de um corpo em queda será sempre
igual a g (10m.s-2).
Escolhendo o sistema de referência da figura cima,
v0 > 0 e g < 0 fica
𝒚 = 𝒚𝟎 + 𝒗𝟎 𝒕 −
𝟏 𝟐
𝒈𝒕
𝟐
𝒗 = 𝒗𝟎 − 𝒈𝒕
Tanto na subida como na descida!
y
𝑔
Se escolhermos outro sistema de referência,
y
v0 < 0 e g>0 fica
𝒚 = 𝒚𝟎 − 𝒗𝟎 𝒕 +
𝟏 𝟐
𝒈𝒕
𝟐
𝒗 = −𝒗𝟎 + 𝒈𝒕
Mais uma vez, tanto na subida como na descida!
𝑔