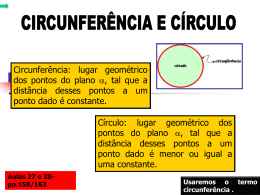
GEOMETRIA ANALÍTICA
CIRCUNFERÊNCIA
CONCEITO:
Circunferência é o conjunto de todos
os pontos de um plano eqüidistantes
de um ponto fixo, desse mesmo plano,
denominado centro da circunferência:
Assim, sendo C(a, b) o centro e P(x, y) um ponto qualquer da
circunferência, a distância de C a P(dCP) é o raio dessa circunferência.
Então:
Geometria Analítica:
Posições relativas entre ponto e circunferência
A aula a seguir traz demonstrações e alguns
exercícios resolvidos de posições que um determinado
ponto pode assumir em relação a uma circunferência.
Dispomos de três possibilidades:
1ª Ponto interno em relação a circunferência.
2ª Ponto pertencente a circunferência.
3ª Ponto externo à circunferência
Geometria Analítica:
Posições relativas entre ponto e circunferência.
Lembre-se:
Geometria Analítica:
Posições relativas entre ponto e circunferência.
Geometria Analítica:
Posições relativas entre ponto e circunferência
Exercício-1: Qual a posição relativa do ponto P(3, 2) em relação à circunferência de equação
x2  y 2  6x  5  0
Substituindo:
3  2  63 5  0
9  4  18  5  0
18  18  0
2
2
Então o ponto P(3, 2) pertence
a circunferência uma vez que a
distância do centro ao ponto P é
igual ao raio.
Geometria Analítica:
Posições relativas entre ponto e circunferência.
Exercício-2: Qual a posição relativa do ponto P(-2, -3) em relação à circunferência de
equação
2
2
2
( x  1)  ( y  4)  ( 5)
Substituindo:
( x  1)  ( y  4)  ( 5)
2
2
2
(2  1)2  (3  4)2  ( 5 )2  0
11 5  0
3  0
Como a distância do centro ao
ponto P em questão é menor
que zero podemos concluir que
o ponto é interno a
circunferência.
Geometria Analítica:
Posições relativas entre ponto e circunferência.
Exercício-3: Qual a posição relativa do ponto P(1, 4) em relação à circunferência de equação
x2  y 2  2x  4 y  21  0
Substituindo:
1  4  2  1  4  4  21  0
2
2
1  16  2  16  21  0
31  21  0
10  0
Nesse caso a distância do
ponto ao centro é maior que
o raio concluímos então que
o ponto é externo à
circunferência
Geometria Analítica:
Posições relativas entre ponto e circunferência.
Resumo final: Quando temos um ponto P(m, n) e uma circunferência
, de centro C(a, b) e raio r, podemos afirmar que:
dcp  r  (m  a)2  (n  b)2  r 2  0  P  
dcp  r  (m  a)2  (n  b)2  r 2  0  P é interno a 
dcp  r  (m  a)2  (n  b)2  r 2  0  P é externo a 
Geometria Analítica:
Posições relativas entre ponto e circunferência.
Créditos da Aula:
Todos os direitos reservados a
Professora: Márcia Regina B Conte.