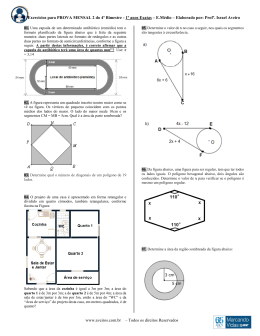
1) Um professor decidiu comprar um notebook no valor de R$3000,00. Como não tinha este dinheiro, utilizou para a compra
seu cheque especial, cuja taxa é de 10% ao mês. Transcorridos trinta dias após a compra, fez um depósito de R$ 700,00,
reduzindo a sua dívida. Sessenta dias após a compra, usou todo o seu salário para quitar completamente a sua dívida. Com
base nas informações acima, determine o valor do salário deste professor.
2) Um artigo publicado na Revista da Sociedade Brasileira de Medicina Tropical em 2004 apresentou um estudo sobre os
fatores de risco para Doenças Sexualmente Transmissíveis (DST) na adolescência. Neste trabalho, foram observadas
associações estatisticamente significativas entre ter uma DST na adolescência e outras variáveis onde destacamos o uso de
drogas lícitas (álcool e tabaco) e ilícitas. A tabela a seguir determina o número de entrevistados que fazem uso de cada um dos
tipos de drogas estudadas divididos em dois grupos: grupo A (portadores de DST) e grupo B (não portadores de DST).
Supondo que
a) todos os componentes do grupo B utilizam um e somente um tipo de droga estudada.
b) todos do grupo A que usam drogas ilícitas também fazem uso das duas drogas lícitas.
c) exatamente dois entrevistados fazem uso das duas drogas lícitas e não fazem uso das ilícitas.
Determine o total dessas pessoas que só fazem uso de bebidas alcoólicas.
3) Além do “Quadrado Mágico” do Parreira, há um outro tipo de Quadrado Mágico que é um antigo quebra-cabeça, encontrado
pela primeira vez na China há 5000 anos. Ele consiste em dispor os inteiros
numa matriz n x n,
que a soma dos números em cada linha, coluna e diagonal da matriz seja sempre a mesma.
Por exemplo,
é um quadrado mágico 3 x 3.
Determine a soma de cada linha, coluna ou diagonal de um quadrado mágico 9 x 9.
, de modo
4)
A figura a seguir representa o gráfico de duas funções polinomiais reais: uma de 1º grau,
, e a outra de
2º grau,
. Observe que os pontos (-1,0), (0,2) e o vértice V da parábola pertencem ao gráfico de
que os pontos (-1,0) e (3,0) pertencem ao gráfico de
.
a) Determine o valor dos números reais
b) Resolva, no conjunto
5)
.
dos números reais, a inequação
Na figura abaixo, sabe-se que
e
,
e
.
.
Determine
a) a medida do segmento DC .
b) a medida do ângulo ADˆ C .
c) a área do triângulo ABC.
6) Se log
3
x denota o logaritmo de x na base 3 e
7) Considere o polinômio
dos números complexos, a equação
, resolva a equação log 3 sen x + log 3 cos x = log 3 tgx − log 3 2 .
. Sabendo que 4i é raiz de
.
, resolva, no conjunto C
8) Um determinado modelo de teclado possui 36 teclas brancas. É também conhecido como modelo de 5 oitavas (cada oitava
representa as teclas brancas DÓ, RÉ, MI, FÁ, SOL, LÁ, SI, DÓ, nesta ordem). A mesma tecla correspondente à nota DÓ, que é
o fim de uma oitava, também, é o início da outra. Neste teclado, a tecla correspondente à nota mais grave, localizada no canto
esquerdo, e a tecla correspondente à nota mais aguda, localizada no canto direito, são teclas correspondentes à nota DÓ,
conforme mostra a figura.
Considere que todas as teclas brancas têm a mesma probabilidade de serem tocadas. Determine a probabilidade de
alguém tocar ao acaso duas teclas brancas distintas correspondentes a uma mesma nota (duas notas DÓ ou duas notas RÉ ou
duas notas SI, etc...).
9) Os fractais são formas geométricas abstratas de uma beleza incrível, com padrões complexos que se repetem infinitamente,
mesmo limitados a uma área finita.O impacto dos fractais é bem evidente, quer na engenharia, nas comunicações, na metalúrgica,
na arte, na matemática e, até, no estudo de doenças crônicas. Este tema tem merecido estudos por parte dos pesquisadores
atuais.
Um exemplo simples de um fractal bastante conhecido é a Curva de Koch também chamada Curva do Floco de Neve.
Ela pode ser construída do seguinte modo:
a) No estágio 1, ela é um triângulo equilátero de lado 1.
b) O estágio
é um polígono obtido a partir do estágio
, dividindo cada lado em três segmentos iguais e construindo
externamente um triângulo equilátero que tem como base o segmento do meio e removendo a seguir esta base.
Abaixo ilustram-se os polígonos obtidos nos estágios 1, 2 e 4 da construção da Curva de Koch.
Polígono 1
Polígono 2
Polígono 3
Polígono 4
a) Determine o lado do polígono 3, representado pela interrogação.
b) Determine o perímetro do polígono obtido no estágio n da construção da Curva de Koch.
10) O prefeito de Mercantinópolis mandou construir, em frente à igreja da matriz, um aquário em forma de cilindro circular reto,
com raio da base 1 metro e volume
metros cúbicos. Em uma clara tentativa de imitar o Museu do Louvre, o mal informado
prefeito ordenou que uma pirâmide regular, cuja base é um triângulo equilátero, fosse colocada dentro do aquário, de modo que
a base da pirâmide ficasse inscrita na circunferência da base do cilindro. A propósito, o prefeito até hoje desconhece que a
pirâmide da entrada do Museu do Louvre tem base quadrada.
Calcule o volume da pirâmide, sabendo que ela tem altura igual à altura do cilindro.