Introdução à Estrutura Atômica
Materiais Elétricos
Introdução à Estrutura Atômica
1 - Introdução a Ciências dos Materiais
Todo projetista está sempre interessado nos materiais que lhe são disponíveis.
Quer seu produto seja uma ponte, um veículo espacial ou um automóvel, deve-se ter um
profundo conhecimento das propriedades características e do comportamento dos
materiais que serão usados em um projeto. Ao fazer a escolha, o projetista deve levar
em consideração propriedades tais como resistência mecânica, condutividade elétrica,
permissividade elétrica, permeabilidade magnética, densidade etc. Além disto, deve-se
considerar o comportamento do material durante o processamento e uso, como por
exemplo, condutores elétricos devem suportar temperaturas extremas e a característica
“tensão/corrente” de um semicondutor deve permanecer inalterada por muito tempo.
A disciplina de Materiais Elétricos tem por finalidade demonstrar os
fundamentos e propriedades dos materiais utilizados nas diversas áreas que envolvem a
eletricidade. Assim, num primeiro instante, o curso apresentará os princípios de
formação da matéria, como o estudo da estrutura atômica, a formação das moléculas, os
materiais condutores, isolantes e semicondutores. No nível macroscópico, o curso
demonstrará o uso destes materiais nos diversos componentes utilizados na eletricidade.
2 - Histórico
Há muitos séculos, o homem observa e experimenta uma grande variedade de
materiais existentes na natureza. No decorrer do tempo, tentou-se explicar a constituição
destes materiais, procurando entender as suas propriedades peculiares. Através de
alguns experimentos realizados por três notáveis cientistas Lavoisier, Proust e Dalton,
chegou-se à hipótese que todo e qualquer tipo de matéria é formado por partículas
minúsculas, chamadas de átomos.
Embora não seja possível observar um átomo, diversas experiências feitas a
partir do século XIX confirmaram a sua existência. Por este motivo a hipótese passou a
ser teoria, e ficou conhecida como a Teoria Atômica de Dalton. Esta teoria criou um
modelo científico sobre o átomo, que ficou conhecido como o Átomo de Dalton,
conforme mostrado na Fig. 1. Segundo este modelo, o átomo deveria ser uma espécie de
“bolinha extremamente pequena, maciça e indivisível”. Este modelo serviu como base
para alguns trabalhos por quase um século, explicando diversos fenômenos. Porém,
novas observações e experimentos demonstraram que o átomo não poderia ser
indivisível.
Fig. 1 – Modelo atômico de Dalton.
O fato de maior relevância que confirmou a divisibilidade do átomo foi a
descoberta da eletricidade,, que conforme os postulados de Coulomb era formada de
cargas elétricas positiva e negativa (TT 301).
301) Assim, o modelo de Dalton não conseguia
explicar o motivo que algumas
algu
soluções “permitiam” a passagem da corrente elétrica e
outrass não. Para explicar este fato, Arrhenius imaginou que as soluções que não
permitiam a “passagem” da corrente eram formadas
formad por moléculas eletricamente
neutras, enquanto
nto que as soluções condutoras possuíam algumas moléculas que estariam
est
divididas em partículas menores, chamadas íons, alguns com carga elétrica positiva,
cátions, e outros com carga negativa, ânions. Estes íons eram responsáveis pelo
transporte da correntee elétrica.
Tentando explicar estes fenômenos, Thomson propôs em 1904 um novo modelo
de átomo, formado de uma “pasta”, com carga elétrica positiva, “recheada” pelos
elétrons, com carga elétrica negativa. A Fig.2 demonstra o modelo atômico de
Thomson. Também,
ém, este modelo considerava que o número de cargas negativas era
igual ao da positiva, garantindo a neutralidade.
Fig. 2 – Modelo atômico de Thomson.
Embora o modelo de Thomson admitisse a divisibilidade do átomo e a natureza
elétrica da matéria, algumas questões ainda não eram claramente explicadas. Por
exemplo, como era possível a retirada de um elétron do átomo formando um íon
positivo ou como um átomo poderia de unir-se a outro átomo e formar uma molécula.
Assim, os cientistas deram continuidade na procura de novos modelos de átomos. A
descoberta de radioatividade foi um passo fundamental para a criação de um modelo
mais completo, sendo Rutherford o cientista responsável pelo desenvolvimento deste
modelo.
3 - O Modelo Atômico de Rutherford
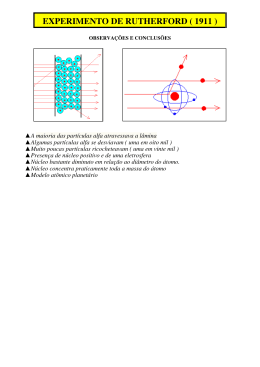
Em 1911, Rutherford utilizou o polônio para emitir um feixe de partículas α
(partículas com carga positiva) sobre uma fina lâmina de ouro, conforme demonstrado
na Fig. 3. Se o modelo atômico de Thomson estivesse correto, estas partículas não
atravessariam a lâmina de ouro. Pois, acreditavam que os átomos eram maciços e
justapostos, como acreditavam Dalton e Thomson. Porém, observou que a maior parte
das partículas α atravessava a lâmina como se fosse uma peneira, apenas uma parte das
partículas desviava ou até mesmo retrocedia. Conforme mostrado na Fig. 4. Desta
forma, Rutherford propôs que a lâmina era constituída de núcleos pequenos, densos e
eletricamente positivos, que repeliam as partículas α.
Fig. 3 – Experimento realizado por Rutherford.
Fig. 4 – Representação da interação das partículas α com os átomos de ouro.
Os “grandes espaços vazios” explicam porque a grande maioria das partículas
atravessava a lâmina sem sofrer desvios. Para completar o modelo, Rutherford imaginou
que ao redor do núcleo estavam girando os elétrons. Sendo negativos, os elétrons iriam
contrabalancear a carga positiva do núcleo e garantir a neutralidade do átomo. Porém,
como cargas opostas de atraem, os elétrons deveriam estar girando ao redor do núcleo.
Se os elétrons estivessem parados, cairiam sobre o núcleo. A Fig. 5 mostra o modelo
atômico de Rutherford.
Fig. 5 – Modelo atômico de Rutherford.
Contudo, o movimento de rotação dos elétrons ao redor do núcleo acabou
trazendo outro conflito em relação à mecânica clássica (teoria eletromagnética clássica
de Maxwell), que diz que toda a partícula elétrica em movimento emite energia na
forma de ondas eletromagnéticas. De acordo com a mecânica clássica, o movimento do
elétron iria consumir energia e sua velocidade de rotação diminuiria até que cair sobre o
núcleo. Este fenômeno só pode ser mais bem compreendido com o uso da mecânica
quântica.
4 – Fundamentos de Mecânica Quântica
A mecânica quântica, como alternativa à formulação tradicional, tornou-se uma
ferramenta necessária para interpretar os fenômenos físicos a nível da estrutura do
átomo, que àquela altura (segunda metade do sec. XIX) começaram a se tornar
acessíveis aos aparelhos de medida. Por exemplo, a luz emitida pelos vários elementos
(espectros) começou a ser analisada e sua composição foi verificada ser característica de
cada um. Ainda, as primeiras partículas elementares (elétrons e prótons) foram
identificadas e seus parâmetros avaliados (tipo de carga elétrica, relação entre massa
inercial e carga elétrica, etc.). Essas e outras iniciativas permitiram a identificação dos
elementos que formam as estrelas, inclusive o nosso Sol, suas massas aproximadas e
temperaturas, e mesmo a descoberta de elementos ainda desconhecidos, e depois
encontrados na Terra (é o caso do gás hélio, detectado em 1868 no espectro da luz solar,
e em 1895 na Terra).
A mecânica quântica surgiu em função de divergências entre os espectros de
emissão analisados pela mecânica clássica e experimentais de corpos negros. Corpo
negro é o nome dado a um corpo idealizado capaz de absorver toda a radiação
eletromagnética que incida sobre ele. Alguns materiais se aproximam de tal idealização,
como placas metálicas pintadas de tinta preta fosca. Tal corpo em equilíbrio térmico
emite radiação na mesma taxa que absorve. O espectro de emissão de um corpo negro é
determinado apenas pela sua temperatura. A Fig. 6 mostra os espectros de emissão de
corpos negros obtidos através da mecânica clássica e observações experimentais.
A explicação para tal espectro, a partir de primeiros princípios, usando a
termodinâmica estatística, eletromagnetismo e a mecânica foi impossível. O melhor
resultado foi obtido por dois físicos Jean e Rayleigh. Através do estudo de emissão de
radiação eletromagnética por uma cavidade de paredes metálicas a uma temperatura T,
eles obtiveram para a densidade espectral J(f) (W2/m2/unidade de freqüência), a
expressão:
=
;
(4.1)
onde K = 1,3807 × 1023 (Joule/K) é a constante de Boltzmann, T a temperatura em graus
Kelvin e f a freqüência em Hz. A expressão (3.1) é conhecida como a lei de RayleighJean e concorda com a intensidade espectral do corpo negro somente para regiões de
baixa freqüência de radiação eletromagnética, conforme demonstrado na Fig. 6.
Observe que (3.1) foi obtida através da energia média por modo de vibração da
cavidade. A energia média, segundo o modelo clássico, é dada por = Nota: uma cavidade é um dispositivo onde a onda eletromagnética sofre
múltiplas reflexões. Através destas reflexões, ocorrem interferências dos tipos
construtivas e destrutivas. Conseqüentemente, após um determinado tempo, somente as
interferências construtivas existirão dentro da cavidade, dando origem aos modos de
ressonância. Este tipo de dispositivo é muito importante para as regiões de Microondas
e Fotônica e será estudado na disciplina de Ondas Guiadas.
Fig. 6 – Intensidade espectral obtida pela lei de Rayleigh- Jean e por medições
experimentais.
Em 1901, Max Planck obteve sucesso em explicar a intensidade espectral de
radiação dos corpos negros, supondo que cada átomo absorve ou irradie apenas
quantidades discretas de energia, chamadas de quantum, dado por:
= ℎ ou ε = ħω;
(4.2)
onde h = ħ / 2π e h é uma constante universal conhecida como constante de Planck e
vale 6,626 × 10-34 (J.s).
Assim, Planck sugeriu que os átomos emissores de radiação se comportassem
como osciladores, que existiriam apenas em estados permitidos, com níveis discretos de
energia. A transição entre estes níveis só seria possível através da absorção ou emissão
de um quantum. Como conseqüência, a energia média por nível discreto de energia não
seria mais dada por KT. Através da probabilidade de Boltzmann de encontrar um
oscilador com energia ε, Planck deduziu uma nova expressão para a energia média, dada
por:
= − ⁄ ∑ ⁄ ;
(4.3)
onde o somatório em n representa a soma dos níveis discretos de energia. A Fig. 7
ilustra a distribuição de energia em um átomo emissor de energia.
6hf
5hf
4hf
3hf
2hf
hf
Fig. 7 – Representação da distribuição discreta dos níveis de energia em um átomo.
Evoluindo (3.3), obtém-se:
= ! "#⁄$% (4.4)
A densidade espectral de um corpo negro passa a ser dado por:
=
ℎ & ! "#⁄$% (4.5)
A expressão (3.5) concorda com os dados experimentais da emissão de um corpo
negro, conforme mostrado na Fig. 5.
A integração de J(f) para todas as freqüências nos fornece a potência por unidade
de área. Esta integral é dada por:
( )
' = *+ + , = ℴ ,
(4.6)
onde ℴ = 5,67 × 10-8 W/m2 K-4 é chamada de constante de Stefan-Boltzmann.
Exemplo: Sabendo que a temperatura em um filamento cilíndrico com 25 µm de raio e 5
cm de comprimento de uma lâmpada incandescente é de 2500º. Calcule a potência
emitida por este filamento. Considere que o filamento seja um corpo negro.
Resposta: PT = 5,67 × 10-8 x (2500 + 273)4 = 3,35 × 106 W/m2.
A potência emitida será P = PT Scilindro = 3,35 × 106 2π 25 × 10-6 5 × 10-2 ≈ 26 W.
5 – O Átomo de Hidrogênio de Bohr
Em 1913, o físico dinamarquês Niels Bohr reuniu as observações, experiências e
as teorias de Rutherford e Planck para aprimorar a explicação do modelo atômico. Uma
dessas observações foi a do comportamento da luz ao atravessar um prisma. Usando um
feixe de luz branca, esta se decompõe num espectro contínuo semelhante ao arco-íris,
que varia gradativamente do vermelho ao violeta, com um espectro muito próximo a um
espectro contínuo. Porém, usando uma luz emitida pelo gás hidrogênio, quando sofre
uma descarga elétrica dentro de um tubo de vidro, o fenômeno era bem diferente,
conforme mostrado na Fig. 8. Pode-se observar que aparecem apenas algumas linhas
coloridas e o restante permanece escuro, ou seja, o espectro passa a ser descontínuo e as
“linhas” são chamadas de raias ou bandas do espectro.
Para resolver o problema do modelo atômico de Rutherford, conforme apontado
no item 4, Bohr propôs que o elétron, ao girar em torno do núcleo, obedeceria à
mecânica quântica e não à clássica. Segundo o modelo de Bohr, o elétron orbitaria em
torno do núcleo em órbitas tais que o momento angular L a ela correspondente fosse
igual a um número inteiro n de ħ, desta forma as órbitas seriam estáveis e o elétron não
“cairia” sobre o núcleo. Uma conseqüência seria que o elétron ocuparia níveis de
energia discretos de acordo com os valores de n. A transição entre os níveis só seria
possível se o elétron emitisse ou absorvesse quantidades discretas de quantum, que na
faixa óptica recebe o nome particular de fóton.
Sol
Hidrogênio
Hélio
Mercúrio
Urânio
Fig 8. – Espectro luminoso da luz emitida pelo sol, Hidrogênio, Hélio, Mercúrio e
Urânio, respectivamente.
Usando o fato de que a força de atração é do tipo eletrostático, e que essa força é
que produz o movimento circular (aceleração centrípeta), temos as relações:
n ħ = m rn2 ωn;
Fmec = m ωn2 rn;
.!/! =
!
,12 3
Nestas equações temos:
e: carga do elétron (1,602×10-19 C);
m: massa inercial do elétron (9,11×10-31 kg);
ε0: permeabilidade elétrica do vácuo (8,85×10-12 F/m);
n: número natural (1, 2, 3...);
rn: raio do movimento orbital circular do elétron;
ωn: pulsação, ou velocidade angular (igual a 2πf).
Combinando-as, obtém-se
4 =
,12 ħ
6! (5.1)
Nesta última equação, verifica-se que somente podem ser aceitas, no modelo de
Bohr, as órbitas eletrônicas cujos raios são múltiplos inteiros (números naturais ao
quadrado, n2) do raio calculado para a primeira órbita (53 × 10-12m). Pode-se verificar,
em seguida, que as energias totais (potencial+cinética) do elétron em cada órbita são as
seguintes:
7 =
6! 12 ħ
= −2,17 × 10
= −13,6
@
(5.2)
Nota: 1 (J) = 1,602×10-19 (eV)
Como se vê, os níveis de energia são quantizados, submúltiplos inteiros (1/n2) da
energia da primeira órbita (n=1). Os valores são negativos porque o elétron está ligado
ao núcleo; se recebem a energia adequada (por exemplo, 13,6 eV quando estão na
primeira órbita), é liberado do núcleo, e o átomo se ioniza.
A transição entre dois níveis n e m gerariam ou absorveriam quantum (fótons) de
energia:
h = ħB = −13,6 C6 − D @
(5.3)
Lembrando que o comprimento de onda pode ser obtido de (5.3) usando f = c/λ.
6 – O Modelo Atômico de Rutherford - Bohr
Com as ponderações de Bohr, o modelo atômico de Rutherford passou a ser
conhecido como o modelo atômico de Rutherford – Bohr. Posteriormente, constatou-se
que as órbitas de todos os átomos conhecidos se agrupam em sete camadas,
denominadas de K, L, M, N, O, P e Q. Em cada camada, os elétrons possuem uma
quantidade fixa de energia, por este motivo são também denominadas de estados
estacionários ou níveis de energia. Além disto, cada camada suporta um número
máximo de elétrons, conforme esquematizado na Fig. 9.
Mesmo depois da contribuição de Bohr no modelo de Rutherford, ainda havia
uma dúvida em relação ao núcleo. Se o núcleo fosse formado apenas por partículas
positivas, haveria uma forte repulsão entre elas e o núcleo se desmoronaria. Assim, em
1932, Chadwick provou que no núcleo não existiam apenas partículas de carga positivo.
Mas, havia a uma terceira partícula com carga neutra, conhecida como Nêutron. De
certa forma, os nêutrons isolariam os prótons. Ao mesmo tempo, os pesquisadores já
haviam percebido a enorme quantidade de energia presente no núcleo, evitando a
repulsão dos prótons. Esta energia ficou conhecida como energia nuclear.
Fig. 9 – Número máximo de elétrons em cada nível de energia.
7 – Evoluções do Modelo Atômico de Rutherford - Bohr
Em 1915, Sommerfeld observou que as linhas espectrais da luz emitida pelo
hidrogênio eram formadas por linhas mais finas e justapostas entre si. Desta forma,
imaginou-se que alguns níveis de energia eram divididos em subníveis, formados por
orbitas circulares e elípticas. Posteriormente, constatou-se que estas “linhas finas” de
algumas raias dos espectros podiam se dividir em linhas ainda mais finas e próximas
quando os átomos de hidrogênio eram expostos a um forte campo magnético. Este fato
indicava que os subníveis descritos acima tinham orientações diferentes no espaço e que
estariam sujeitas a diferentes momentos magnéticos para uma dada força magnética.
Porém, devido às restrições nos experimentos da época, estes subníveis não foram
totalmente compreendidos.
Em uma outra experiência, os átomos de Hidrogênio emissores de luz foram
submetidos a um forte campo magnético. Mais uma vez, observou que as linhas
espectrais eram divididas em duas. Como o átomo de Hidrogênio possui apenas um
elétron, conclui-se que os elétrons deveriam possui um movimento de rotação sobre si
próprio, que foi denominado de Spin. O Spin criaria um campo magnético que
possibilitaria o desvio do feixe de átomos do Hidrogênio sob a influência de um campo
magnético externo.
Em paralelo ao estudo dos níveis
níveis e subníveis, alguns pesquisadores se
preocupavam em estudar a natureza das partículas elementares, principalmente a do
elétron. Assim sendo, em 1923 De Broglie levantou
levan
a hipótese do comportamento dual
da matéria. De Broglie passou a visualizar o elétron
elétron não mais como uma “bolinha”
girando em torno do núcleo,
núcleo mas como uma partícula-onda.
onda. Isto é, atribuiu ao
movimento do elétron todas as características da propagação das ondas, como
freqüência, amplitude, comprimento de onda etc.. A Fig. 10 ilustra o movimento
mo
do
elétron ao redor do núcleo, segundo a hipótese de De Broglie.
Fig. 10 – Modelo atômico de De Broglie.
Nota: No início do século XX, já havia sido constato que para explicar certas
propriedades da luz era melhor imaginá-la
imaginá como uma partícula. Isto
sto levou Einstein a
propor, em 1905, que a luz seria formada por partículas-onda.
partículas
. Esta teoria levou a De
Broglie a considerar o movimento de uma partícula como uma onda.
A sugestão de De Broglie foi que partículas com momento p poderiam ser
associadas à onda
nda de comprimento de onda λ, dada por:
E=F
(7.1)
Esta suposição explicava as órbitas estáveis do modelo de Bohr. Para uma órbita
com raio r,, a condição de que o comprimento da órbita seja igual a um múltiplo inteiro
do comprimento de onda λ do movimento do elétron ao redor do núcleo garantia a
estabilidade das órbitas. Ou seja:
2G4 = E
(7.2)
É importante salientar que no caso de De Broglie, o comprimento de onda λ seria
obtido através de relações não-relativistas e pode ser escrito como:
E=F=
√6I
(7.3)
Exemplo: Quais os comprimentos de onda de um elétron com energia de 1 (eV)
e de uma bala de 10 gramas movimentando-se paralelamente à superfície da terra a uma
velocidade de 600 m/s.
Resposta:
E! =
12,26 × 10J
K7@
= 12,26 Å
No caso da bala, a energia total será a energia cinética 7 = M@ ⁄2
EN =
6,626 × 10&,
K10 ×
10& 600
= 1,1 × 10&, M
Através do resultado da bala, pode-se verificar que o pequeno comprimento de
onda resulta numa elevada freqüência 3×108/1,1×10-34 = 2,72×1042 Hz. Se
considerarmos variações de 2,72×1042 em 1 segundo para as dimensões de uma bala,
conclui-se que o resultado seria um movimento retilíneo, conforme analisado pela
mecânica clássica. No caso do elétron, a freqüência resultante seria 2,44 ×1017 Hz, que,
embora sendo uma alta freqüência, o movimento ondulatório da partícula não pode ser
desprezado, principalmente se levarmos em conta as dimensões do elétron, cujo raio é
muito menor que o comprimento de onda calculado.
A hipótese de De Broglie foi confirmada através de experimento realizado em
1927 por Davison e Gerner. Neste trabalho, verificaram que a difração dos elétrons de
baixa energia apresentavam um comportamento igual à difração do raio-X, que é uma
onda eletromagnética de alta freqüência.
O exemplo anterior mostra que o movimento ondulatório das partículas
elementares não pode ser desprezado. Assim, as dimensões atômicas do elétron
associada à sua alta freqüência impossibilitariam determinar a sua correta localização.
Os próprios instrumentos de medições iriam alterar essas determinações. Por isto
Heisenberg, em 1926, afirmou que não é possível calcular a posição e a velocidade de
um elétron, num mesmo instante. Este fato ficou conhecido como Princípio da Incerteza
de Heisenberg, que tem o seguinte princípio:
“O
produto
das
incertezas
(dispersões)
nas
medidas
de
grandezas
complementares referentes ao estado de um objeto nunca pode ser inferior à constante
de Planck, dividida por 2π (ħ, portanto).”
As grandezas complementares a que se refere o texto são naturalmente aquelas
para as quais o produto das dimensões (unidades de medida) é dimensionalmente igual à
constante de Planck, ou seja, ação (energia x tempo). São mais utilizadas as seguintes:
∆x (incerteza na posição em x) ⋅ ∆px (momento linear no eixo x) ≥ ħ
∆E(variação de energia) ⋅ ∆t(instante da variação) ≥ ħ
∆ω(velocidade angular) ⋅ ∆[mωr2](momento angular) ≥ ħ
Para ilustrar o princípio, o próprio Heisenberg propôs exemplos: num destes, se
procura medir a posição de um elétron por meio de um poderoso microscópio. A luz
que ilumina a partícula deve ter um comprimento de onda muito menor do que o do
objeto, para poder medir com acuidade sua localização; mas então, a partícula sofrerá
um forte impacto deste fóton, pois quanto menor λ maior a energia e o momento linear.
O momento linear da partícula será fortemente alterado, de tal maneira que será muito
grande a incerteza sobre o seu estado anterior, se quisermos identificá-lo. A posição
pode ser determinada com a precisão que se quiser, mas o momento linear torna-se
difícil de identificar.
Devido à dificuldade de calcular a posição exata do elétron, Schrödinger foi
levado a calcular a região no espaço onde haveria a maior probabilidade de encontrar o
elétron. Esta região no espaço foi denominada de orbital.
8 – Equação de Schrödinger
Quase simultaneamente aos fatos descritos anteriormente, apareceu uma
formulação, na forma de uma equação diferencial, elaborada por Erwin Schrödinger. A
integração dessa equação diferencial dá uma função Ψ(x,y,z,t) que rege todo o
comportamento das partículas, como posição, energia, velocidade, momento linear ou
angular etc. Embora na época se visse com reservas a adoção de uma grandeza de tão
incômoda interpretação, os resultados encontrados se mostraram extremamente
animadores e, hoje em dia, essa formulação é a preferida em textos introdutórios. Ainda,
o resultado da operação ∫Ψ⋅Ψ*dv, estendida a um volume V, tem interpretação física: é a
probabilidade de se encontrar a partícula (cuja função descritiva é Ψ de complexo
conjugado Ψ* ) dentro do volume V; portanto, a integral definida de um volume infinito
(todo o universo!) deve ser igual a 1. Outra conseqüência: a posição média da partícula
(x) é dada por ∫ΨxΨ*dv.
A forma clássica de apresentar esta equação diferencial é em coordenadas
cartesianas, conforme abaixo:
−
ℏ ∇ QR,S,T,U
6
+ @W, X, Y, Z[W, X, Y, Z = \ℏ
]QR,S,T,U
]U
(8.1)
A equação de Schrödinger é uma equação convencional a derivadas parciais,
onde temos a constante de Planck e a massa da partícula (ħe m), uma energia potencial
V(x,y,z,t) e, no segundo membro, a derivada parcial em relação ao tempo. A fim de
verificar a aplicação de (8.1), consideremos um potencial unidimensional. Este é um
caso de aplicação da equação de Schrödinger de relativamente restrita aplicação prática,
mas interessante sob o ponto de vista didático. O potencial unidimensional tem uma
distribuição em relação somente à coordenada x. Dentro de um intervalo (-a < x < +a),
o potencial V é nulo e fora desta região o potencial possui um valor negativo muito
grande, tendendo a -∞, conforme Fig. 11. Portanto, nossa partícula de carga negativa
(elétron) está confinada na região especificada, mas dentro dela é livre (V=0); ainda,
para preservar a continuidade de Ψ(x,t), esta deve se anular nos pontos x = ±a.
V→ -∞
V→ -∞
V=0
-a
a
Fig. 11 – Representação de um potencial unidimensional.
Como o potencial é constante no tempo, pode-se empregar o método de
separação de variáveis para a resolução de (8.1).
[W, X, Y, Z = ^W, X, Y_Z
(8.2)
Substituindo (8.2) em (8.1), tem-se
−
ℏ ∇ `R
6
]aU + @W^W = \ℏ^W
]U aU
= 7b ,
(8.3)
onde Ej é a constante de integração. Como no intervalo de -a até a o potencial á nulo e a
função ψ, obtém-se de (8.3):
−
ℏ `R
6 R aU = ^W7b ;
\ℏ aU
U aU
= 7b
(8.4)
As soluções das equações diferenciais (8.4) apresentam-se de forma tabelada e
podem ser encontradas em qualquer livro de cálculo. Assim, tem-se:
^W = cb Wd e
fK6Ig
ℏ
Wh + ib Wd e
_Z = Wd C
fIg
ℏ
fK6Ig
ℏ
Wh
(8.5)
ZD
(8.6)
A constante de integração da solução temporal foi escolhida como 1, pois tratase de um valor aceitável e cômodo. As constantes Aj e Bj de integração devem ser
escolhidas conforme as condições de contorno. Reescrevendo (8.5), tem-se:
^W = cb + ib jkl e
K6Ig
ℏ
Wh + \cb + ib l e
K6Ig
ℏ
Wh
(8.5)
É preciso lembrar que a função ψ(x) deve ser sempre nula nos pontos x=±a.
Examinando a sua forma na equação, percebemos que não pode haver anulação
simultânea das duas parcelas, pois seno e cosseno não são zero nos mesmos pontos;
conclui-se que uma das duas componentes da solução deve ser completamente anulada.
Uma escolha conveniente é de Aj=Bj, eliminando a parte complexa da solução de ψ(x).
O resultado passa a ser então:
K6Ig
^W = mb jkl e
ℏ
Wh
(8.6)
Outra escolha possível é de anular a parte real, conservando a complexa; neste
caso temos Ak=-Bk, e a forma da solução passa a ser:
K6Io
^W = \mn l e
ℏ
Wh
(8.7)
A determinação dos valores aceitáveis para a energia Ej passa agora pela
exigência de concordância da função nos pontos x=±a. Para o caso de Aj=Bj, a solução
é a da parte real:
K2M7b
p = ±r + 0,5G; r = 0, 1, 2 ,3 ….
ℏ
7b =
bvJ,*
6w
ℎ
(8.8)
Da mesma forma, quando se tem a solução em seno (complexa) temos outros
valores para Ek:
K2M7n
p = ±xG; r = 0, 1, 2 ,3 ….
ℏ
n
7n = 6w ℎ
(8.9)
Em cada caso de nível de energia (Ej ou Ek) a constante de integração (Cj ou Ck)
deve ser calculada de forma que a probabilidade de se encontrar o elétron em algum
ponto, para –a < x < +a seja unitária: essa é a etapa de normalização da função de onda.
Essa normalização é calculada da seguinte forma:
vw
y [W, Z [ ∗ W, Z{W = 1
w
Em cada caso o valor do produto escalar é independente do tempo, pois a função
τj,k(t) é puramente complexa, de módulo igual a 1, e portanto neste caso o seu produto
pelo complexo conjugado é também 1. A integral deve, portanto, ser calculada sobre
ψ(x), e resulta, em cada caso:
vw
vw
y [W, Z [ ∗ W, Z{W = jb y jkl |r + 0,5GW⁄p} {W
w
w
vw
y [W, Z [
w
∗ W,
Z{W =
vw
jn y l |xGW⁄p} {W
w
Calculadas as integrais e normalizado o resultado (igualado a 1), resultam para
as constantes Cjk os valores:
mb = mn = 1~p
(8.10)
Na figura 12, temos um esboço da configuração das várias soluções de ψ(x), em
relação à j e k. Como se pode observar, as ondulações espaciais de ψ(x) descrevem as
ondulações do elétron dentro do potencial unidimensional, conforme De Broglie havia
suposto.
ψjk(x)
√1/a
j=0
-a
+a
x
j=1
k=1
-√1/a
Fig. 12 – Representação das funções ψjk(x), soluções da equação de Schrödinger, para
o elétron confinado a um plano de espessura 2a.
9 – As soluções da Equação de Schrödinger para o Átomo
O grande triunfo da equação de Schrödinger foi a aplicação dos conceitos de
Bohr: o átomo de hidrogênio. Neste caso, a resolução se harmonizou perfeitamente com
os experimentos descritos anteriormente no item 7, que a mecânica quântica preliminar
deixara em aberto, como a questão dos subníveis e os orbitais. Com o sucesso desta
equação sobre o átomo de Hidrogênio, abria caminho para a sua aplicação em átomos
mais pesados e um entendimento da configuração da Tabela Periódica. Os resultados
obtidos são descritos na seqüência.
9.1 – Estados Energéticos dos Elétrons
De acordo com os resultados obtidos pela equação de Schrödinger, chegou-se à
conclusão de que os átomos se dispõem ao redor do núcleo conforme o Diagrama
Energético mostrado na Fig. 13.
Fig. 13 - Diagrama Energético do átomo.
a) Níveis Energéticos: São as sete camadas que aparecem no diagrama, com
níveis de energia crescente, denominadas de K, L, M, N, O, P, Q.
Atualmente, estes níveis são conhecidos como Número Quântico Principal.
b) Subníveis Energéticos: Conhecidos como Número Quântico Secundário
ou Azimutal (l). São os “degraus” de cada escada do diagrama. Para todos
os átomos conhecidos, l assume os valores de 0, 1, 2 e 3, designados pelas
letras s, p, d e f. O número quântico secundário corresponde às “linhas finas”
observadas por Summerfeld em 1915.
c) Orbitais: Cada subnível comporta um número de orbitais, conforme
demonstrado na Fig. 14. Os orbitais são identificados como Número
Quântico Magnético (Ml ou m). Devido às orientações espaciais dos
orbitais, criam-se momentos diferentes para os elétrons quando os átomos
são expostos ao um mesmo campo magnético. Por esta razão, recebeu este
nome.
Fig. 14 – Distribuição dos números quânticos magnéticos no Diagrama Energético do
átomo.
d) Spin: Spin é o nome dado à rotação do elétron sobre o seu eixo central. Pela
equação de Schrödinger, pode-se constar que cada orbital suporta no máximo
dois elétrons. Como os elétrons possuem carga negativa, é necessária a
atração magnética entre os elétrons. Desta forma, os spins deverão ser
opostos. Este fato ficou conhecido como Princípio da Exclusão de Pauli, e
é identificado pelo Número Quântico de Spin (Ms ou s) cujo os valores são
-1/2 e 1/2. Para representá-los no diagrama energético adota-se:
representa, por convenção, um spin negativo,
representa, por convenção, um spin positivo
9.2 – Orbitais
A forma geométrica dos orbitais também é obtida através da equação
Schrödinger.
Os orbitais s – a subcamada s tem um orbital. Podemos dizer que a distribuição
da densidade de probabilidade para um elétron s é esfericamente simétrica.
Os orbitais p - a subcamada p tem 3 orbitais. No átomo isolado, esses três
orbitais têm a mesma energia e a mesma densidade de probabilidade para o elétron. Os
orbitais p têm a forma de haltere, com dois lobos separados por um nó. Eles diferem
entre si pela sua orientação no espaço. Usando um sistema de coordenadas
tridimensionais cartesianas podemos representar os três como: px, py e pz.
Os orbitais d - A subcamada d consiste em cinco orbitais, representados por dx,
dy, dz, dx2-y2 e dz2. No átomo isolado, todos eles têm energias equivalentes.
Os orbitais f - Os orbitais f são ainda mais complexos que os orbitais d. Eles são
importantes apenas para a química dos elementos lantanóides e actinóides.
A Fig. 15 mostra a forma geométrica de alguns orbitais.
Fig. 15 – Forma geométrica de alguns orbitais.
Para o preenchimento do diagrama energético, algumas regras deverão ser
levadas em conta:
a) Os elétrons vão se encaixando na eletrosfera, partindo dos níveis e subníveis
de menor para os de maior energia (isto é, de baixo par cima), só passamos para um
subnível superior quando o inferior já estiver “lotado”(Regra da energia mínima)
b) Num mesmo subnível, de início, todos os orbitais devem receber seu primeiro
elétron e, só depois cada orbital passará a receber seu segundo elétron( esssa é chamada
Regra de Hund ou regra da Máxima Multiplicidade)
c) Num orbital o primeiro elétron é, por convenção, o de spin -1/2
Considerando a descrição acima, o elétron passa a possuir um endereço dentro
do átomo, descrito como:
Para ilustrar o exposto acima, considere a distribuição dos 26 elétrons do Ferro
no diagrama energético, mostrado na Fig. 16.
Fig. 16 – Distribuição dos elétrons do átomo de Ferro no diagrama energético.
A distribuição dos elétrons do átomo de Ferro é dada por 1s2 2s2 2p6 3s2 3p6 4s2
3d6.
Para facilitar a distribuição dos elétrons no átomo, Linus Pauling desenvolveu
um novo diagrama, conhecido como Diagrama de Pauling. A Fig. 17 ilustra este
diagrama.
Fig. 17 – Diagrama de Pauling.
Para o preenchimento do diagrama de Pauling, devem-se percorrer as diagonais
no sentido indicado, colocando o número máximo de elétrons permitido em cada
subnível até completar o número total de elétrons.
Exemplo: Utilizando o diagrama de Pauling e considerando o tungstênio (W) de
número atômico (número de prótons) igual a 74, responda as seguintes questões.
a) Qual a distribuição eletrônica do tungstênio por camadas ou níveis
energéticos?
b) Qual a distribuição por subníveis energéticos?
c) Quais os elétrons mais externos?
d) Quais os elétrons com maior energia?
Resposta:
5d4
a) A distribuição por camadas fica; K=2, L=8, M=18, N=32, O=12, P=2.
b) Por subníveis: 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d10 5p6 6s2 4f14 5d4
c) Os elétrons mais externos ou afastados são os elétrons do subnível 6s, pois
pertencem à camada P.
d) Os elétrons de maior energia são os quatro elétrons do subnível 5d, pois foi o
último subnível preenchido.