Tópicos Avançados em Estrutura de Dados
6º Período – Ciência da Computação
Ordenação de dados (parte 1)
Ordenação é o processo de arranjar um conjunto de informações semelhantes em uma dada ordem, seja ela
crescente ou decrescente.
Os algoritmos de ordenação dividem-se em duas grandes categorias: Algoritmos de ordenação de matrizes e
algoritmos de ordenação de arquivos seqüenciais. Foca-se aqui nos algoritmos de ordenação de matrizes pois
estas estruturas são as mais utilizadas na área de computação.
Há três métodos gerais para se ordenar dados em matrizes.
1.
2.
3.
Ordenação por troca
Ordenação por seleção
Ordenação por inserção
Vamos fazer uso de um baralho para exemplificarmos cada método.
Ordenação por troca
1) Espalhe as cartas voltadas para cima:
2) Troque as cartas fora de ordem até que todo o baralho esteja ordenado
Ordenação por seleção
1) Espalhe as cartas voltadas para cima:
2) Escolha a carta de menor valor e coloque em sua mão:
3) Repita o processo até ter todas as cartas ordenadas em sua mão:
Ordenação por inserção
1) Segure em suas mãos as cartas todas embaralhadas
2) Coloque uma carta por vez na mesa, inserindo ela na ordem correta. Repita até terminar as cartas.
Algoritmos de ordenação simples
Ordenação Bolha, Bublesort ou O demônio das Trocas
É o método de ordenação mais conhecido e mais difamado. Sua popularidade deve-se pela sua simplicidade
de implementação e pela facilidade de guardar seu nome. Contudo é uma das piores ordenações já
concebidas.
Leva esse nome pois se pensarmos em uma matriz de elementos na forma vertical, os elementos menores
sobem (quando ordenado crescentemente), dando a representação de uma bolha de ar que sobe num líquido.
Veja:
5
3
4
1
2
5
3
3
3
3
3
3
1
1
3
5
4
4
4
1
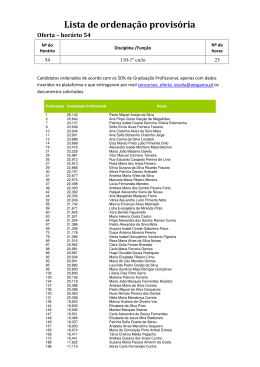
1
3
2
4
4
5
1
1
4
2
2
3
1
1
1
5
2
2
4
4
4
2
2
2
2
5
5
5
5
5
O bublesort é uma ordenação por troca.
Uma das implementações do bublesort é dada abaixo:
#include
#include
#include
#include
<string.h>
<stdio.h>
<stdlib.h>
<conio.h>
void bolha (char *matriz, int numEle);
int main () {
char s[80];
printf ("Informe uma string a ser ordenada: ");
gets(s);
bolha(s, strlen(s));
//strlen retorna o tamanho de uma string
printf("\nA string ordenada eh: %s. \n", s);
getch();
}
/* Bublesort */
void bolha (char *matriz, int numEle)
{
register int a, b;
register char t;
//register cria variaveis de CPU que sao mais rapidas que variaveis de memoria
for (a=1; a<numEle; ++a)
for (b=numEle-1; b>=a; --b) {
if (matriz[b-1] > matriz[b]) {
/* troca os elementos */
t=matriz[b-1];
matriz[b-1]=matriz[b];
matriz[b]=t;
}
}
}
A partir do código informado anteriormente e da matriz dada pelos elementos dcab, a ordenação dar-se-ia da
seguinte forma:
Matriz inicial:
Passo 1:
Passo 2:
Passo 3:
d
a
a
a
c
d
b
b
a
c
d
c
b
b
c
d
A ordenação via bublesort é uma ordenação do tipo n-quadrada, pois seu tempo de execução é um múltiplo
do quadrado do número de elementos da matriz a ser ordenada. Ordenações do tipo n-quadrada o tempo esta
diretamente associado a quantidade de elemento que é quem determina a quantidade de comparações e trocas
a serem realizadas.
A ordenação por troca do bublesort sempre executa
comparações. Onde n é o número de
elementos.
Melhor caso: 0 comparações para uma lista já ordenada.
Médio caso:
comparações.
Pior caso:
comparações.
Há várias maneiras de se melhorar a ordenação Bolha. Uma das mais utilizadas é a inversão da direção da
leitura dos elementos entre os passos subseqüentes. A essa melhoria no bublesort deu-se o nome de
ordenação oscilante ou shaker.
Abaixo o código da função shaker. Basta substituir a função bolha no código anterior e testar.
/* Shakersort */
void shaker (char *matriz, int numEle)
{
register int a;
int troca;
register char t;
//register cria variaveis de CPU que sao mais rapidas que variaveis de memoria
do {
troca=0;
for (a=numEle-1; a>0; --a){
if (matriz[a-1]>matriz[a]) {
t=matriz[a-1];
matriz[a-1]=matriz[a];
matriz[a]=t;
troca=1;
}
}
for (a=1; a<numEle; ++a){
if (matriz[a-1]>matriz[a]) {
t=matriz[a-1];
matriz[a-1]=matriz[a];
matriz[a]=t;
troca=1;
}
}
} while (troca); //ordena ate que nao aja mais trocas
}
Mesmo sendo uma melhora do bublesort o shakersort ainda continua sendo uma ordenação n-quadrada.
Ordenação por Seleção
Neste método de ordenação é selecionado o elemento de menor valor e este é trocado pelo primeiro elemento
da matriz a ser ordenada. Logo para os n-1 elementos restantes, é encontrado o elemento menor e este é
trocado pelo segundo elemento e assim por diante. As trocas continuam até os últimos dois elementos.
Vejamos um exemplo. Se este método fosse aplicado à matriz bdac:
Matriz inicial:
Passo 1:
Passo 2:
Passo 3:
b
a
a
a
d
d
b
b
a
b
d
c
c
c
c
d
/* ordenação por seleção */
void select (char *matriz, int numEle)
{
register int a, b, c;
int troca;
register char t;
//register cria variaveis de CPU que sao mais rapidas que variaveis de memoria
for (a=0; a<numEle-1; ++a){
troca=0;
c=a;
t=matriz[a];
for (b=a+1; b<numEle; ++b) {
if (matriz[b]<t) {
c=b;
t=matriz[b];
troca=1;
}
}
if (troca) {
matriz[c]=matriz[a];
matriz[a]=t;
}
}
}
A ordenação por seleção é considerada muito lenta quando se possui uma quantidade de elementos grandes a
serem ordenados.
Melhor caso: 3(n -1) comparações.
Pior caso:
comparações.
Ordenação por inserção
Este método é o último dos três algoritmos de ordenação simples. Na ordenação por inserção primeiramente
é ordenado os dois primeiros elementos da matriz. Em seguida o algoritmo insere o terceiro elemento na sua
posição já ordenada em relação aos dois primeiros elementos. Então o quarto elemento é inserido na ordem,
com base nos três elementos anteriores já ordenados, e assim por diante.
Vejamos um exemplo. Dada à matriz dcab:
Matriz inicial:
Passo 1:
Passo 2:
Passo 3:
d
c
a
a
c
d
c
b
a
a
d
c
b
b
b
d
/* ordenação por inserção */
void insert (char *matriz, int numEle)
{
register int a, b;
register char t;
//register cria variaveis de CPU que sao mais rapidas que variaveis de memoria
for (a=1; a<numEle; ++a){
t=matriz[a];
for (b=a-1; b>=0 && t<matriz[b]; b--)
matriz[b+1]=matriz[b];
matriz[b+1]=t;
}
}
Contrariando o método bolha e a ordenação por seleção, na ordenação por inserção a quantidade de
comparações depende de como a lista está inicialmente ordenada. Se a lista estiver ordenada a
quantidade de comparações será n-1, caso contrário a quantidade de comparações será
Melhor caso: 2(n - 1)
Médio caso:
Pior caso:
Exercícios na próxima página.
Exercícios:
1) Demonstre passo a passo como ficaria a ordenação crescente da matriz [ghbjdalefcik], pelos
método bolha, método de seleção e método de inserção;
2) Demonstre passo a passo como ficaria a ordenação crescente da matriz [642135], pelos método
bolha, método de seleção e método de inserção;
3) Implemente em C todos os códigos presentes aqui.
Extras
4) Implemente, sem o uso de ponteiros, os algoritmos descritos nesta apostila.
Referências Bibliográficas:
SCHILDT, Herbert. C Completo e Total. São Paulo: Makron Books, 1996.
TENEMBAUM, Aeron. Estruturas de Dados usando C. São Paulo: Makron Books, 1995.