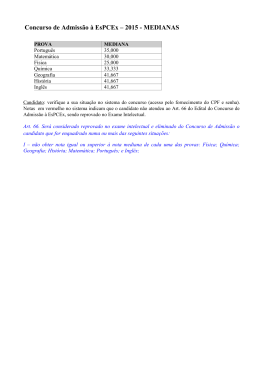
42.º CONCURSO DE ADMISSÃO AO CFS 1.
Num saco estão 12 bolas, sendo 6 brancas, 4 pretas e 2 azuis. Deste saco, retira-se uma
bola, ao acaso.
Qual é a probabilidade de a bola retirada ser azul?
2.
(A)
50% + 𝑃 𝑠𝑎𝑖𝑟 𝑏𝑜𝑙𝑎 𝑝𝑟𝑒𝑡𝑎
(B)
𝑃 𝑠𝑎𝑖𝑟 𝑏𝑜𝑙𝑎 𝑏𝑟𝑎𝑛𝑐𝑎 − 𝑃 𝑠𝑎𝑖𝑟 𝑏𝑜𝑙𝑎 𝑝𝑟𝑒𝑡𝑎
(C)
17%
(D)
100% + 𝑃 𝑠𝑎𝑖𝑟 𝑏𝑜𝑙𝑎 𝑏𝑟𝑎𝑛𝑐𝑎 𝑜𝑢 𝑏𝑜𝑙𝑎 𝑝𝑟𝑒𝑡𝑎
Uma turma do ensino básico obteve as seguintes classificações na avaliação final, na
disciplina de matemática.
𝐶𝑙𝑎𝑠𝑠𝑖𝑓𝑖𝑐𝑎çã𝑜
1 2 3 4 5 𝑁ú𝑚𝑒𝑟𝑜 𝑑𝑒 𝑎𝑙𝑢𝑛𝑜𝑠
2 6 10 8 2 Quais são os valores da média, da moda e da mediana? (O valor da média está
arredondado às centésimas.)
3.
(A)
𝑀é𝑑𝑖𝑎 = 3,07 ; 𝑚𝑜𝑑𝑎 = 3 ; 𝑚𝑒𝑑𝑖𝑎𝑛𝑎 = 3
(B)
𝑀é𝑑𝑖𝑎 = 3,17 ; 𝑚𝑜𝑑𝑎 = 3 ; 𝑚𝑒𝑑𝑖𝑎𝑛𝑎 = 3
(C)
𝑀é𝑑𝑖𝑎 = 3,18 ; 𝑚𝑜𝑑𝑎 = 5 ; 𝑚𝑒𝑑𝑖𝑎𝑛𝑎 = 3
(D)
𝑀é𝑑𝑖𝑎 = 3,17 ; 𝑚𝑜𝑑𝑎 = 5 ; 𝑚𝑒𝑑𝑖𝑎𝑛𝑎 = 3 Seja 𝑓 uma função definida por 𝑓 𝑥 = 𝑘𝑎 ! , com 𝑘 ∈ ℝ e 𝑎 ∈ ℝ! \ 1 .
Os pontos de coordenadas 0 , 5 e 3 , 40 pertencem ao gráfico da função 𝑓 .
Quais são os valores de 𝑘 e de 𝑎 ?
(A)
𝑘 = 5 e 𝑎 = 8
(B)
𝑘 = 5 e 𝑎 = 2
(C)
𝑘 = −5 e 𝑎 = −2
(D)
𝑘 = 5 e 𝑎 = −2
PAC MATEMÁTICA – 1.ª CHAMADA – VERSÃO 1 Página 2 de 7 42.º CONCURSO DE ADMISSÃO AO CFS 4.
Na figura ao lado, está representada a reta 𝑟 que contém
os pontos de coordenadas 0 , 2 e 3 , 0 .
A equação reduzida da reta 𝑟 é:
5.
𝑦 𝑟 2
𝑥−2
3
(A)
𝑦=
(B)
𝑦 = 3𝑥 − 2
(C)
𝑦=−
(D)
𝑦 = −3𝑥 + 2
𝑥 2
𝑥+2
3
Considere o polinómio: 9𝑥 ! − 12𝑥 + 4 .
Uma fatorização deste polinómio é:
6.
(A)
9𝑥 − 2
!
(B)
(C)
3𝑥 − 2 3𝑥 + 2
(D)
3𝑥 − 1 3𝑥 − 1
3𝑥 − 2 ! Uma equação do tipo 𝑎𝑥 ! + 𝑏𝑥 + 𝑐 = 0 , com 𝑎 ≠ 0 , é impossível se:
(A)
𝑏 ! − 4𝑎𝑐 < 0
(B)
𝑏 ! − 4𝑎𝑐 > 0
(C)
𝑏 ! − 4𝑎𝑐 = 0
(D)
𝑏 ! − 4𝑎𝑐 ≤ 0
PAC MATEMÁTICA – 1.ª CHAMADA – VERSÃO 1 Página 3 de 7 42.º CONCURSO DE ADMISSÃO AO CFS 7.
8.
Considere a seguinte representação gráfica de uma função, de domínio ℝ\ 0 .
O gráfico é uma hipérbole, cujas assíntotas são os eixos coordenados.
Qual é a expressão analítica desta função?
!"
(A)
𝑦=−
(B)
𝑦 = 40𝑥
(C)
𝑦=
(D)
𝑦 = 40𝑥 + 4
!
!"
!
O domínio da função, real de variável real, definida por 𝑓 𝑥 = 6 − 3𝑥 é:
(A)
−∞, 2
(B)
−∞, 2
(C)
2, +∞
(D)
2, +∞
2𝑥 + 𝑦 = 1
9.
Qual dos pares ordenados
(A)
1
, 0
2
(B)
𝑥 , 𝑦
é solução do sistema 0 , 1 (C)
4𝑥 +
y
=2
2
0 , 4 ?
(D)
0 ,
1
2
10. Sejam 𝐴 = −1 , 2 e 𝐵 = −𝜋 , 0 .
Em qual das seguintes opções está representado o conjunto 𝐴 ∪ 𝐵 ?
(A)
𝑥 ∈ ℝ ∶ 𝑥 > −1 ∧ 𝑥 < 0 (B)
𝑥 ∈ ℝ ∶ 𝑥 > −𝜋 ∧ 𝑥 < 0 (C)
𝑥 ∈ ℝ ∶ 𝑥 > −1 ∧ 𝑥 < 2 (D)
𝑥 ∈ ℝ ∶ 𝑥 > −𝜋 ∧ 𝑥 < 2 PAC MATEMÁTICA – 1.ª CHAMADA – VERSÃO 1 Página 4 de 7 42.º CONCURSO DE ADMISSÃO AO CFS 11. Os três primeiros números triangulares (1 , 3 e 6) estão representados na figura.
3.
Qual das seguintes expressões pode ser o termo geral da sucessão dos números
triangulares?
4.
(A)
2𝑛 − 1
(B)
! !!!
!
(C)
!!!!
!
(D) 2𝑛 + 1
12. Na escola do Daniel, 50% dos alunos gostam de ler livros de ficção científica.
Dos alunos que gostam de ler livros de ficção científica, 20% gostam de livros policiais.
De entre todos os alunos da escola do Daniel, qual é a percentagem de alunos que gostam
de ler os dois géneros de livros?
(A)
10%
(B)
15%
(C)
25%
(D)
30%
13. Qual das seguintes relações está correta?
(A)
4,7×10! < 3,4×10!
(B)
4,7×10! < 3,4×10!
(C)
4,7×10! < 340×10!
(D)
4,7×10!! < 4,7×10!!
14. Qual dos seguintes números é um número irracional?
(A)
6,4
(B)
1
64
PAC MATEMÁTICA – 1.ª CHAMADA – VERSÃO 1 (C)
0,64
(D)
−
2
3
Página 5 de 7 42.º CONCURSO DE ADMISSÃO AO CFS 15. Sendo 𝑎 e 𝑏 dois números reais, positivos e diferentes, qual das igualdades seguintes é
verdadeira?
5.
!
(A)
𝑎 𝑏
= 𝑎𝑏
(B)
(C)
𝑎+𝑏 = 𝑎+ 𝑏
(D)
!
!! !
!
! !
=
!! !
!!!
= 𝑏
16. Qual das afirmações seguintes é verdadeira?
(A)
ℝ! ∪ ℝ! = ℝ
(B)
!
ℚ!
! ∩ ℝ! = ∅
(C)
ℚ∩ℝ=ℚ
(D)
ℤ∪ℝ=ℤ
17. Cada aula de Matemática da Rita tem 50 minutos de duração.
Ela desafiou os colegas de outra turma a descobrirem quantas aulas de Matemática já havia
tido este ano, dizendo-lhes: “Já tive 4,2 × 10! minutos de aulas de Matemática”.
Quantas aulas de Matemática já teve a Rita este ano?
(A)
81
(B)
82
(C)
83
(D)
84
18. A área de um triângulo equilátero é igual a 𝑎 cm2, sendo 𝑎 um número positivo.
A área, em cm2, de um triângulo semelhante, cujo comprimento do lado seja o triplo do lado
do primeiro, é:
(A)
3 𝑎
(B)
𝑎!
PAC MATEMÁTICA – 1.ª CHAMADA – VERSÃO 1 (C)
6 𝑎
(D)
9 𝑎
Página 6 de 7 42.º CONCURSO DE ADMISSÃO AO CFS 19. As possíveis distâncias entre dois vértices de um cubo de aresta 1 são:
(A)
1 ,
2 e 3
(B)
1 e 2
(C)
20. De um certo ângulo agudo 𝛼 , sabe-se que cos 𝛼 =
1 ,
2 e 3
(D)
1 ,
(D)
7
16
3 e 2
3
.
5
Qual é o valor de sen 𝛼 ?
(A)
9
25
(B)
3
2
(C)
4
5
FIM
PAC MATEMÁTICA – 1.ª CHAMADA – VERSÃO 1 Página 7 de 7