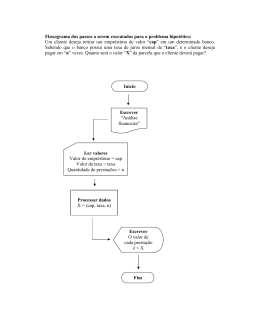
Matemática Financeira- 2015/01
Prof. Eduardo Meliga Pompermayer
Lista 2
1) João tem uma dívida de R$ 35.000,00 que vence em 16 meses. Pretende
pagar R$12.000,00 no fim de 158 dias e R$ 13.000,00, 189 dias depois desse
primeiro pagamento. Quanto deve pagar na data de vencimento de modo que
liquide a dívida? Considere juros simples de 50% a.a. e data focal no
vencimento da dívida.
2) Um capital acrescido de seus juros de 21 meses soma R$ 156.400,00. O mesmo capital
diminuído de seus juros de 9 meses é reduzido a R$ 88.400,00. Calcular o capital
investido e a taxa de juros ganha, considerando que operação foi realizada no Regime
de Capitalização Simples.
3) Uma pessoa aplicou dois capitais a juros simples, o primeiro a 33% aa e o segundo a
45% aa. Se o rendimento de ambas as aplicações totalizou R$ 52.500,00 no prazo de
um ano, determinar o valor dos capitais, sabendo-se que o primeiro é 37,5% menor
que o segundo
4) Uma empresa obteve um empréstimo de R$ 200.000,00 a juros simples de 10%
aa. Algum tempo depois liquidou a dívida, inclusive juros, e tomou um novo
empréstimo de R$ 300.000,00 a juros simples de 8% aa. Dezoito meses após o
primeiro empréstimo liquidou todos seus débitos, tendo pago R$ 35.000,00 de juros
totais nos dois empréstimos. Determinar os prazos dos dois empréstimos em meses.
5) Uma pessoa tomou um empréstimo a juros simples de 9% aa; 45 dias depois pagou a
dívida e contraiu um novo empréstimo duas vezes maior do que o primeiro, pelo prazo
de 10 meses, a juros simples de 6% aa. Sabendo-se que pagou ao todo $ 111.250 de
juros, calcular o valor do primeiro empréstimo.
6) Dois capitais foram colocados a juros simples, o primeiro à taxa de 20% a.a. e o
segundo a 40% a.a. Calcular os capitais sabendo que somados montam $ 500,00 e que
os dois produziram em um ano juros totais de $ 130,00.
7) Uma pessoa levantou um empréstimo de $3000 a juros simples de 18% a.a. para ser
liquidado daqui a 270 dias. Se a pessoa amortizou $1000 no 75 dia, quanto deverá
pagar na data do vencimento para liquidar a dívida? (data focal: 270 dia)
8) Calcular:
9) o rendimento de um capital de $ 2.000 aplicado a juros simples de 2,5% a.m. desde o
dia 12 de março até o dia 5 de junho do mesmo ano;
10) O valor do capital que rendeu $ 3.000 no período compreendido entre 4 de abril e 31
de maio do mesmo ano a juros simples de 2% a.m.;
11) O valor de resgate de um capital de $5.000 aplicados a juros simples de 2% a.m. pelo
período compreendido entre 6 de abril e 26 de junho do mesmo ano;
12) O capital que se transformou em um montante de $ 20.000 no período compreendido
entre 30 de junho e 31 de dezembro do corrente ano, a juros simples de 2% a.m.;
13) A taxa mensal de juros simples mensal obtida por uma aplicação de $24.000 que
rendeu $ 2.800 no período compreendido entre 23 de maio e 18 de agosto do mesmo
ano.
14) No dia 26 de maio foi contratado um empréstimo de $7.000 a juros simples de 24%
a.a. para ser totalmente liquidado em 90 dias. No dia 16 de junho foram amortizados
$3.000, e no dia 11 de julho, $2.500. Determinar a data de vencimento da dívida e o
valor da quantia que deverá ser paga naquela data para liquidar a dívida (considerar
ano civil e data focal no 90° dia).
15) Uma dívida de $2.000 contraída no dia 8 de junho para ser liquidada no dia 8 de julho
foi ontratada originalmente a juros simples de 2% a.m.. Calcular o rendiment da
aplicação, sabendo-se ue a taxa de juros subiu para 2,5% a.m. no dia 12 de junho, para
3% a.m o dia 24 de junho e para 3,5% a.m. no dia 3 de julho
16) Hoje, uma pessoa tem duas dívidas: a primeira, de $8.000, vence em 36 dias, e a
segunda, de $12.000, vence em 58 dias. A pessoa propõe-se a quitá-las por meio de
dois pagamentos iguais dentro de 45 e 90 dias, respectivamente. A juros simples de
24% a.a., calcular o valor de cada pagamento (data focal: 90° dia).
17) Calcular o montante de uma aplicação de $3.500 pelas seguinte taxas de juros
e prazos: a) 4% a.m., 6 meses
b) 8% a.t., 18 meses
c) 12% a.a., 18
meses
18) Em que prazo um capital de $18.000 acumula um montante de $83.743 à taxa
de 15% a.m.?
19) Um capital de $51.879,31 aplicado por seis meses resultou em $120.000. Qual
a taxa de juros efetiva ganha?
20) Na compra de um bem cujo valor à vista é $140, deve-se pagar uma entrada
mais duas prestações de $80 no fim dos próximos dois meses. Considerandose uma taxa de juros efetiva de 20% a.m., qual o valor da entrada?
21) Qual o tempo necessário para que seja triplicada uma população que cresce à
taxa composta de 3% a.a.?
22) Um produto cujo preço à vista é $450 será pago em duas prestações mensais
consecutivas de $280 e $300, a primeira para 30 dias. Considerando-se que a
taxa de juros embutida na primeira prestação é 10% a.m., determinar a taxa
embutida na segunda.
23) O valor à vista de um bem é de $6.000. A prazo, paga-se uma entrada mais
três parcelas mensais de $2.000 cada, sendo a primeira em um mês. Calcular
o valor da entrada, considerando-se que a taxa de juros aplicada é 7% a.m..
24) Um capital de $50.000 rendeu $1.000 em um determinado prazo. Se o prazo
fosse dois meses maior, o rendimento aumentaria em $2.060,40. Calcular a
taxa de juros efetiva ao mês ganha pela aplicação e o prazo em meses.
25) Certo capital, após quatro meses, transformou-se em $850,85. Esse capital,
diminuído dos juros ganhos nesse prazo, reduziu-se a $549,15. Calcular o
capital e a taxa de juros efetiva ao mês ganha na aplicação.
26) Uma pessoa tomou dois empréstimos. O primeiro por 3 meses a juros efetivos
de 5% a.m., e o segundo por 10 meses a 4% a.m.. Sabendo-se que os juros
pagos pelos dois empréstimos totalizaram $11.181,14 e que o primeiro
empréstimo é igual à metade do segundo, calcular o valor total dos
empréstimos.
27) Uma empresa tem duas dívidas. A primeira, de $10.000, contratada a juros
efetivos de 3% a.m., vence em 48 dias, e a segunda, de $15.000, a juros
efetivos de 4% a.m., vence em 63 dias. A empresa pretende liquidar as dívidas
com o dinheiro proveniente do desconto financeiro de uma promissória com
valor nominal de $27.033 que vence em 90 dias. Calcular a taxa mensal efetiva
aplicada pelo banco no desconto do título.
28) Quanto tempo é necessário para que a relação entre um capital de $8.000,
aplicado a juros efetivos de 4% a.m., e seu montante seja igual a 4/10?
29) Três dívidas, a primeira de $2.000 com vencimento em 30 dias, a segunda de
$1.000 com vencimento em 60 dias e a terceira de $3.000 com vencimento em
90 dias serão liquidadas por meio de um pagamento único de $6.000. Se a
taxa de juros efetiva aplicada for de 3% a.m., determinar daqui a quanto tempo
deve ser efetuado esse pagamento.
30) Um capital de $20.000 foi aplicado por 90 dias à taxa efetiva diária de 0,1%
a.d.. Determinar o rendimento ganho entre o 46o e o 87o dia .
31) Uma pessoa necessita dispor de $20.000 daqui a 8 meses. Para tanto,
pretende efetuar duas aplicações em um fundo que rende juros efetivos de 3%
a.m.. A primeira aplicação, de $10.000, foi efetuada hoje, e a segunda o será
daqui a um mês. De quanto deverá ser esta segunda aplicação de modo que a
pessoa possa dispor da quantia necessitada ao término do oitavo mês?
32) Um empréstimo de $5.000 foi tomado a juros efetivos em 14 de abril e
liquidado por $5.850 em 28 de maio do mesmo ano. Determinar a taxa efetiva
mensal contratada. (considere o ano civil)
2)
1) $2.231,95
2,083333%a.m.(25%
a.a.) P = 108.800
3) P1 = $50.000
4) n1= 3 meses,
P = $80.000
n2= 15 meses
8) a) $141,66
5) $1.000.000
9) 24 de agosto
6) P1 = $350
P2 = $150
7) $2.307,50
10) $55
11) $10.120,20
13) 11 meses
14) 15% a.m.
17) 23,89% a.m.
18) $751,37
15) $17,78
19) 2% a.m
21) $30.000
22) 5% a.m
25) $875,98
26) $5.961,83
$1.708,67
1 mês
23) 23 meses e 11
dias
27) 11,2988% a.m
b) P = $78.947,37
c) $5.270
d) P = $17.814,73
e) i = 4,023% a.m.
12)a) $ 4.428,62
b) $ 5.554,06
c) $ 4.148,54
16) 37,17 anos
20) $700
5% a.m.
24) = 65 dias