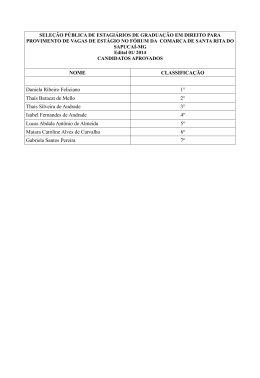
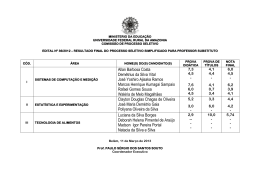
Engenharia Econômica
Demétrio E. Baracat
Cap. 3 A Variável Tempo
3.1 — A EQUIVALÊNCIA, O VALOR DO DINHEIRO NO TEMPO
Imaginemos uma situação na qual eu já saiba hoje que dentro de um ano terei de efetuar um
pagamento no valor de 1.100 reais. Se dispuser de dinheiro hoje, será que é indiferente efetuar
este pagamento hoje (adiantado) ou dentro de um ano? A resposta é não efetuá-lo hoje! Se eu
o efetuar hoje, terei que desembolsar 1.100 reais. Se eu deixar para pagar dentro de um ano (no
vencimento) posso investir 1.000 reais a prazo fixo (que supomos dar 10% ao ano) — isto me
garante ter os 1.100 reais daqui a um ano para efetuar o pagamento, e lucrar hoje mesmo 100
reais com esta operação.
Se, no mesmo exemplo, o problema for, aproveitar um desconto especial e pagar 1.000 reais
hoje ou R$1.100 dentro de um ano? Sou indiferente a qualquer das duas possibilidades.
Entretanto, prefiro pagar 999 reais hoje do que 1.100 dentro de um ano. Prefiro pagar 1.100
dentro de um ano do que 1.001 reais hoje.
Portanto, o dinheiro não tem o mesmo valor através do tempo (observe que neste contexto
não estamos considerando ou analisando inflação – isto será feito oportunamente). Não
entramos em considerações relativas a preferências pessoais com compra a prestação, (e assim
pagar juros) ou aversões às dívidas (portanto pagamento à vista). A argumentação está sendo
feita em termos estritamente econômicos. Por outro lado, supusemos que as únicas alternativas
existentes fossem pagar já ou investir a prazo fixo e, portanto efetuar o pagamento dentro de
um ano.
Pagamentos diferentes em sua magnitude total, mas que são feitos em datas diferentes podem
se tornar equivalentes. Vários capitais são ditos equivalentes quando os seus valores
transferidos para a mesma data, com a mesma taxa de desconto (neste caso, o custo de
oportunidade), são iguais. Assim, para o caso em análise, tem-se a equivalência:
ou, em termos gerais, Va =
Vf
1+ i
14
04/08/09
3:24
Engenharia Econômica
Demétrio E. Baracat
onde i é a taxa de desconto referente ao período considerado, Va é chamado de valor atual e Vf
é o valor futuro. Como i corresponde ao período inteiro em consideração (no caso ano), é
chamado de taxa simples.
O termo (1 + i) é a parcela que permite a comparação entre valores em tempos diferentes.
A taxa de desconto pode corresponder a um custo de oportunidade, a uma taxa de juros ou
simplesmente refletir a preferência de um indivíduo baseado no intervalo de tempo
considerado. Observe que é sempre um valor individual e temporal
— varia de um indivíduo para outro ou de uma firma para outra, e no intervalo considerado.
3.2 —OS JUROS SIMPLES
Se um parente me empresta o dinheiro a 10% a.a. e ao fim de um ano, cobrar 1.100 reais por
um empréstimo de 1.000, o cálculo terá sido:
1100 = 1000(1 + 10%) , onde i = 0,1=10%.
Se o mesmo empréstimo, em vez de ser por um ano, tiver sido por três anos e meu familiar
cobrar 1.300 reais, o cálculo terá sido executado como:
1300 = 1000(1 + 3 ∗ 10%)
Este é o caso de juros simples. A relação é, para n períodos:
Vf = Va (1 + n ∗ i)
3.3 —OS JUROS COMPOSTOS
Se investirmos um capital K no início de um período, a uma taxa de juro i no período,
recuperaremos no final do período o total K + iK = K(1 + i) , onde o termo iK corresponde
à renda do capital investido. Se todo o capital disponível no fim do primeiro período for
novamente investido durante mais um período à mesma taxa de juros i, ter-se-á ao final deste
segundo período K (1 + i)(1 + i) = K (1 + i) 2
Este cálculo é chamado de juros compostos. O cálculo considera juros compostos quando os
juros para cada período forem baseados na quantia total devida ao término do período
anterior, quantia esta que inclui o principal inicial mais os juros acumulados que são pagos ao
final do período.
Dependendo do caso, os períodos poderão ser anos, ou então meses, ou mesmo semanas ou
até dias. Também podemos calcular a equivalência destas taxas em outros períodos. Podemos,
por exemplo, calcular a equivalência de um capital de 1.000 aplicado a 12% ao ano durante 3
anos por meio de juros simples resultando 1000(1 + 3 ∗ 12% ) = 1360 . O mesmo cálculo
com juros compostos anualmente resulta 1000 (1 + 12% )3 = 1406 . Finalmente, o mesmo
cálculo para juros compostos anuais de 12% mas capitalizados mensalmente resultaria:
15
04/08/09
3:24
Engenharia Econômica
Demétrio E. Baracat
12% ⎞
⎛
1000⎜ 1 +
⎟
12 ⎠
⎝
36
= 1430 .
No presente texto/curso, a não ser que haja uma ressalva específica, sempre
consideraremos os juros como sendo compostos.
Podemos então comparar a equivalência entre um valor presente Va e um futuro Vf ao fim de
n períodos com cálculo de juros compostos, considerando os juros como i por período através
de:
Vf = Va (1 + i) n .
Analogamente, o valor atual equivalente a uma seqüência de três pagamentos, A1, A2 e A3
efetuados dentro de um, dois e três anos correspondentemente, resulta, por meio de cálculo
com juros compostos, à soma de todas as parcelas após tê-las transportadas para o instante
t=0. Só é possível comparar ou somar parcelas quando elas estiverem referidas ao
mesmo ponto no tempo.
Va =
Em termos gerais, Va =
N
A3
A1
A2
+
+
1 + i (1 + i)2
(1 + i)3
A
∑ (1 + i i)n
n =1
onde, se A > 0 corresponder a receitas, e A <0 corresponde a despesas. Para representar os
fluxos monetários e o instante em que ocorrem utilizaremos um referencial cartesiano. Os
fluxos monetários estarão representados no eixo vertical, serão ascendentes quando forem
receitas, e descendentes quando forem desembolsos. O eixo horizontal representará o instante
considerado para o fluxo monetário. Ou seja, podemos visualizar um fluxo de dinheiro como
na Figura 2-1.
Figura 3-1 Fluxo monetário
16
04/08/09
3:24
Engenharia Econômica
Demétrio E. Baracat
A este fluxo de receitas e despesas corresponde um valor presente ou atual calculado como
acima explicado. Também podemos achar um valor futuro no último período.
Na Figura 2-1, a receita A1 é convencionada como sendo referente ao primeiro período.
Queremos deixar bem claro que vamos adotar a convenção de fim de período isto é, vamos
concentrar os valores referentes a um determinado período sempre aplicados no fim do
período correspondente.
A equivalência não é só entre pagamentos em um só ponto no tempo, mas pode ser entre
séries de pagamentos ou receitas. A equivalência dependerá da taxa de desconto (custo de
oportunidade, ou juros) usada. Se várias séries são equivalentes a uma determinada taxa
de desconto, elas poderão não ser equivalentes para outras taxas de desconto.
Em princípio, utilizaremos quatro tipos básicos de configuração de fluxos ao longo de n
períodos.
a)Valor atual Va,
b) Valor Final ou Valor Futuro Vf,
c) Anuidade Uniforme A,
d) Gradiente uniforme G,
17
04/08/09
3:24
Engenharia Econômica
Demétrio E. Baracat
É possível converter o valor dos fluxos de uma configuração em outra configuração
equivalente. As fórmulas correspondentes são as seguintes:
Vf
Va
1
=
Vf
(1 + i)n
Va
(1 + i)n − 1
=
A
i(1 + i) n
Va
(1 + i)n − 1 − ni
=
G
i2 (1 + i) n
A
1
n
= −
G
i (1 + i) n − 1
Va
= (1 + i)n
A
i(1 + i) n
=
Va
(1 + i)n − 1
ou
G
i2 (1 + i) n
=
Va
(1 + i)n − 1 − ni
G
1
=
1
n
A
−
i
(1 + i) n − 1
3.4. APLICAÇÃO DO VALOR ATUAL NA ANÁLISE DE PROJETOS
Uma das técnicas de análise bastante difundidas é calcular o valor atual equivalente de uma
série correspondente às receitas e desembolsos de uma proposta e comparar este valor com o
investimento necessário para iniciar o empreendimento. Se o equivalente da receita e
desembolsos superar o investimento inicial (desembolso inicial), a proposta será aceita.
EXEMPLO 3-1
Mancadas & Cia estão estudando diversas alternativas de investimentos para o próximo ano.
As quantias a serem investidas e as rendas anuais correspondentes estão indicadas abaixo.
Todas as propostas têm a mesma vida de 20 anos, após os quais não há nada recuperável sobre
o investimento inicial.
A firma considera que seu custo de oportunidade em relação a não investir é 10% ao ano, isto
é, o retorno mínimo aceitável para empreender uma atividade é de 10% ao ano. Não há
limitação de capital disponível, de modo que toda proposta julgada rentável será aceita. Só se
permite investir em um projeto de cada tipo. Quais os projetos que se qualificam?
18
04/08/09
3:24
Engenharia Econômica
Demétrio E. Baracat
Proposta
Investimento Inicial
necessário
Renda Anual
Líquida
A
B
C
D
E
F
30.000
50.000
100.000
150.000
170.000
200.000
3.250
6.500
8.500
17.650
11.750
24.200
Solução:
Chamando de A a renda anual, o problema consiste em calcular o valor atual dos rendimentos
auferidos.
Vai =
20
A
∑ (1 + i i)n
n =1
= Ai J
Podemos encontrar uma quantia maior ou menor que o investimento correspondente inicial.
Se for maior, é sinal de que a proposta rende mais do que 10% ao ano, e deve ser aceita. O
valor J assim determinado
J =
20
1
∑ (1 + i)n
n =1
= 8,514
representa o fator multiplicativo a ser aplicado à parcela A (renda líquida anual)
Então resulta:
Proposta
A
B
C
D
E
F
Valor Atual
Va = 8514 ∗ 3250 = 27671
Decisão
Rejeita
Va = 8514 ∗ 6500 = 55341
Aceita
Va = 8514 ∗ 8500 = 72369
Rejeita
Va = 8514 ∗ 17650 = 150272
Aceita
Va = 8514 ∗ 11750 = 100040
Rejeita
Va = 8514 ∗ 24200 = 206039
Observe que, com i = 15%, resulta, J =
20
1
∑ (1 + i)n
n =1
Aceita
= 6,259
e, para a proposta B, Va = 40.683,50. Compare este resultado com o anterior e pense a
respeito.
Observe que o valor de Va varia de um indivíduo (ou firma) para outro segundo o valor de i. O
valor de Va não é uma medida objetiva e universal.
À taxa de desconto de i = 10% teríamos a tendência de dizer que o projeto B é melhor que o
projeto F. De fato, pela intuição, chamando de benefício à renda total descontada (e levada
para t = 0) e de custo do investimento (que está em t = 0), uma relação benefício/custo resulta
19
04/08/09
3:24
Engenharia Econômica
Demétrio E. Baracat
1,107 para o projeto B e 1,030 para o projeto F. Entretanto, esta conclusão pode ser enganosa,
pois o investimento é muito menor para B do que para F. Pergunta-se: Supondo que a empresa
disponha de 200.000 e resolva investir 50.000 em B, o que fazer com os 150.000 restantes? Se a
resposta for investir em D, então para um investimento conjunto (B + D) resulta uma relação
benefício/custo igual a 1,028, que é menor do que para o projeto F.
No presente exemplo, como os projetos não são excludentes (realizar um não implica em
desistir de outro), o resultado é que, sendo i = 10%, convém aceitar B, D e F.
3.5 — ANÁLISE DE ALTERNATIVAS POR VALOR ATUAL
A finalidade do presente texto é discutir critérios econômicos para a análise de alternativas.
No caso da Figura 2-2, a alternativa I é evidentemente sempre melhor que a alternativa II, pois
a cada período seus valores são dominantes (nunca inferiores).
FIGURA 3-2
20
04/08/09
3:24
Engenharia Econômica
Demétrio E. Baracat
No caso da Figura 3-3, a análise entre as alternativas III e IV já não é tão simples. A somatória
das parcelas pura e simplesmente é inviável, pois a priori, não temos meio de saber se uma
parcela de 500 no período 2 vale mais ou menos que uma parcela de 600 no período 3.
FIGURA 3-3
O método do Valor Atual consiste em transferir todos os valores para o ponto t = 0. Dadas
diversas alternativas é possível calcular os valores atuais equivalentes às séries correspondentes
e compará-los para decidir qual a melhor.
EXEMPLO 3.2
Um incinerador de lixo de 1.000 ton/dia de capacidade necessita de R$ 50.000.000,00 de
investimento e opera a um custo variável de R$ 50/ton. Um incinerador de lixo de 500 ton/dia
de capacidade necessita R$ 30.000.000,00 de investimento e opera a um custo variável de R$
55/ton. A demanda de serviços ao longo de 10 anos é :
tempo(ano)
1
2
3
4
5
6
7
8
9
10
ton/dia
300
350
400
450
500
600
700
800
900
1000
21
04/08/09
3:24
Engenharia Econômica
Demétrio E. Baracat
Deseja-se limitar o horizonte do projeto, para fins de análise, em 10 anos.
a) Sabendo que o custo do capital é de i = 7% ao ano, escolha entre as duas alternativas:
I) construir já (início do período 1) um incinerador de 1000 ton/dia.
II) construir já um incinerador de 500 ton/dia e outro igual no início do período 6 (ou seja, fim
do período 5).
b) Repita o problema se o custo do capital for i = 18°/o ao ano.
Solução: Vamos calcular o valor atual de todos os custos. Consideremos o ano de 360 dias.
a) Para a alternativa I, resulta:
⎛ 300
1000 ⎞
350
400
⎟ =
+
+
+
+
...
Va = 50.000.000 + 50 * 360⎜⎜
2
3
10 ⎟
1
,
07
1
,
07
1
,
07
1
,
07
⎝
⎠
R$120.409.152
Para a alternativa II, resulta
Va = 30.000.000 +
30.000.000
1,07
5
⎛ 300
350
400
1000 ⎞
⎟ =
+ 55 * 360⎜⎜
+
+
+ ... +
2
3
1,07
1,07 10 ⎟⎠
⎝ 1,07 1,07
R$128.839.653
De modo que concluímos pela alternativa I, por ser a mais econômica
b) Neste caso
VaI = R$90.473.463
VaII = R$87.634.085
De modo que optaríamos pela alternativa II.
O presente exemplo mostra bem o valor do dinheiro no tempo, pois no caso b o custo do
capital é tal que compensa adiar parte do investimento por cinco anos e perder as economias
de escala de um incinerador de maior capacidade.
Observe-se que o método do valor atual só permite comparar alternativas sob as mesmas
condições, isto é, o mesmo valor para a taxa de desconto i e, mesma duração de projeto. No
caso a a melhor alternativa é a I e no b é a II. Observe que como os horizontes são diferentes
tivemos que efetuar a análise sob um mesmo denominador.
EXEMPLO 3-3
Você
pretende
renovar
a
assinatura
Superhipermeganalistafinanceiro” Os preços são:
da
sua
revista
predileta
“O
1 ano R$ 700
2 anos R$ 1.200
22
04/08/09
3:24
Engenharia Econômica
Demétrio E. Baracat
3 anos R$ 1.600
Supõe-se que não exista inflação.
Você costuma depositar suas economias mensais em instituições financeiras que lhe dão i =
6% ao ano. Qual o plano mais vantajoso?
Solução:
Supomos sempre querer ler a revista durante os próximos anos, de modo que o custo total será
comparado para o total de seis anos, por ser múltiplo comum dos anos 1, 2 e 3. Só assim, após
tornar os serviços da leitura idênticos, podemos comparar as alternativas.
a) Assinatura anual
Valor atual dos gastos
700 +
700
700
700
700
700
+
+
+
+
= R$3619 :
1,06 1,062 1,06 3 1,06 4 1,06 5
b) Assinatura de dois em dois anos
Valor atual dos gastos
1200 +
1200
1,06
2
1200
+
1,06 4
= R$3218
c) Assinatura a cada três anos
Valor atual dos gastos
1600 +
1600
1,06 3
= R$2943
e, assim a assinatura da revista de três em três anos é a mais vantajosa.
3.6. — JUROS NOMINAIS E EFETIVOS
Quando um juro nominal de i% ao ano for composto em intervalos de tempo menores que
um ano, o resultado é um juro efetivo maior que o nominal quando comparado na mesma
base. O efetivo é, pois, o valor equivalente ao que seria o juro se ele fosse composto uma só
vez por período.
A caderneta de poupança que rende juros de i = 6% nominais ao ano e pagos trimestralmente,
e portanto que paga 1,5% por trimestre, corresponde a taxa de juros efetiva anual aos quatro
pagamentos de 1,5%.
23
04/08/09
3:24
Engenharia Econômica
Demétrio E. Baracat
(1 + itri )4
= 1 + ianual →
4
6% ⎞
⎛
⎜1 +
⎟ = 1 + ianual →
4 ⎠
⎝
ianual = 6,136%
Recomendamos ao leitor verificar que, se a composição fosse semestral, o valor da taxa de
juros efetiva seria 6,09% ao ano.
Se a taxa anual fosse de 12% com composição mensal resultaria, após um ano, em
(1 + imes )12
= 1 + ianual = (1 + 0,01) 12 →
ianual = 12,682%
de modo que a taxa efetiva é de 12,682% ao ano.
EXEMPLO 3-4
Qual a taxa de juros anual efetiva real de um empreendimento que rende juros nominais de
i=10% por trimestre?
Solução:
(1 + jtri )4
= 1 + ianual = (1 + 10%) 4 = 1,464 →
ian = 46,4% a.a.
EXEMPLO 3-5
Desejo comprar um objeto que me é oferecido à prestação em 24 meses. A forma de pagar é
R$ 1.000,00 de entrada e mais vinte e quatro pagamentos iguais de R$ 1.000,00, perfazendo um
total de R$ 25.000,00. Todo dinheiro poupado costuma ser investido na caderneta de
poupança, que, costuma dar i = 6% ao ano, pagos trimestralmente. Qual o valor máximo que
eu estaria disposto a pagar pelo mesmo objeto a vista?
Solução:
Primeiramente observamos que 6% ao ano pagos trimestralmente corresponde a
1
6% 4
(1 +
) − 1 = 0,37% am . De modo que a resposta é
4
Va
(1 + i)n − 1
(1 + 0,37% )24 − 1 = R$23924,72
=
→
V
=
1000
+
1000
a
A
i(1 + i) n
0,37%(1 + 0,37%) 24
24
04/08/09
3:24
Engenharia Econômica
Demétrio E. Baracat
3.7. CÁLCULO PARA COMPOSIÇÃO CONTÍNUA
Vimos que
Va
1
=
onde n é o número de períodos. Se os juros forem compostos m
Vf
(1 + i)n
vezes por período, temos
Vf
i ⎞
⎛
= ⎜1 + ⎟
Va
m⎠
⎝
nm
e, se a composição dos juros for continua, teremos que calcular o limite para m → ∞ , e então
V
a expressão acima, resulta f = e in onde e = 2,718 base dos logaritmos neperianos.
Va
Na prática, se os juros anuais forem compostos diariamente o resultado não é
significativamente diferente do caso da composição contínua.
Se desejarmos saber a taxa de juros efetiva correspondente a uma taxa nominal de 6% ao ano
composta continuamente, calculamos
1 + i = e i = 1,06 → i = ln 1,06 = 0,0583 → i = 5,83%
EXEMPLO 3-6
A companhia farmacêutica FarmaCrazy decidiu aumentar suas atividades por meio de um
novo xarope expectorante para todos aqueles que estão sadios e gostariam de iniciar um
processo tussígeno. Isto vai requerer novos investimentos, e o grupo de engenharia organizou
um diagrama que resulta nos seguintes gastos:
1° de Janeiro de 2010 — Pagamento inicial da construção
1° de Agosto 2010 — Pagamento do fim da construção
31 de Dezembro 2011 — Compra de Equipamento
31 de Dezembro 2012 — Operação e Manutenção
31 de Dezembro 2013 — Operação e Manutenção
31 de Dezembro 2014 Operação e Manutenção
31 de Dezembro 2015 Operação e Manutenção
31 de Dezembro 2016 — Operação e Manutenção
Investimento
200.000
600.000
500.000
Gasto anual
150.000
150.000
170.000
190.000
170.000
150.000
A firma tem diversas possibilidades de investimentos, e adota uma taxa de 16% a.a. como
sendo o custo de oportunidade do dinheiro.
Despreze valores residuais para equipamentos e instalações. Empregue a convenção de fim de
período.
25
04/08/09
3:24
Engenharia Econômica
Demétrio E. Baracat
Há uma proposta de por meio de um investimento adicional de 60.000 em 31 de Dezembro de
2012, estabilizar os gastos de operação e manutenção em 150.000 até o fim da vida do produto
(31 de Dezembro 2016). Deve-se aceitar esta proposta?
Solução
A proposta corresponde a um investimento de 60.000 no fim do período 4. A economia, dada
pela diferença entre a proposta sem investimento adicional e a proposta com investimento
adicional, levada para o fim do período 4, resulta em
20.000
40.000
20.000
+
+
= 59.780
2
1 + 0,16 (1 + 0,16)
(1 + 0,16)3
Portanto, a proposta deve ser rejeitada, já que o benefício 59.780 (economia) é menor que o
investimento 60.000, ambos comparados em um mesmo ponto no tempo.
3.8 — CONCEITOS ADICIONAIS SOBRE EQUIVALÊNCIA DE FLUXOS
Até agora vimos como comparar fluxos por meio de seus valores equivalentes em um ponto
no tempo, isto é, comparando valores atuais. Evidentemente, poderíamos obter as mesmas
conclusões comparando valores finais.
Quando estudamos alternativas nas quais as receitas e desembolsos ocorrem nos mesmos
períodos, é comum ser vantajoso transformar todos os valores de cada série em uma série
equivalente uniforme de mesma periodicidade para cada alternativa e comparar os elementos
da série. As conclusões resultam idênticas às comparações em um ponto no tempo. A série de
valores uniformes é chamada de equivalente uniforme periódico, ou equivalente uniforme
anual (EUA).
Alguns fluxos envolvem receitas e despesas que crescem ou decrescem uniformemente.
26
04/08/09
3:24
Engenharia Econômica
Demétrio E. Baracat
EXEMPLO 3-7 Sejam os fluxos
O primeiro gráfico ilustra o fluxo monetário de um certo projeto. O segundo gráfico
representa o mesmo fluxo que o anterior alterado para um modo equivalente para facilitar os
cálculos que se seguem.
i) A primeira série é um fluxo uniforme positivo de nove parcelas de valor + 20 de t=0 até t =
8, o que dentro da convenção de fim de período corresponde a ter sua origem em t=-1 seu
valor atual é:
Va
Va
(1 + 0,10 )9 − 1
(1 + i)n − 1
→ Va = 115,18
=
ou
=
20
0,10(1 + 0,10 )9
A
i(1 + i) n
ii) a segunda parcela é um fluxo uniforme negativo de seis parcelas de valor — 20, de t= 9 até t
= 14 (ou seja, origem em t = 8); seu valor atual em t=-1 é:
27
04/08/09
3:24
Engenharia Econômica
Demétrio E. Baracat
Va
Va
(1 + 0,10 )6 − 1
(1 + i)n − 1
ou
→ Va = −36,67
=
=
0,10(1 + 0,10 )6
− 20
A
i(1 + i) n
iii) A terceira parcela é um gradiente uniforme com origem em 0, de valor — 10 e com nove
períodos; seu valor atual em t=-1 é:
Va
(1 + i)n − 1 − ni
Va
(1 + 0,10 )9 − 1 − 9 * 0,10
=
ou
=
→ Va = −190,41
G
− 10
0,10 2 (1 + 0,10 ) 9
i2 (1 + i) n
Somando as três parcelas resulta: Va = −111,9
Levando este valor para t = 0,
Va = — 111,9 x 1,1=
— 123,1
Desejando a resposta em
V
(1 + i)n − 1
(1 + 0,10 )14 − 1
− 123,1
→
=
→ A = EUA = −16,7
EUA a =
A
A
i(1 + i) n
0,10 (1 + 0,10 )14
EXEMPLO 3-8
Deseja-se vender um terreno, por qualquer dos dois seguintes planos:
a) ou 20.000 à vista ou b) x a prazo.
O plano a prazo exige 50% de entrada e 50% em 24 prestações mensais iguais calculadas, para
o cliente, a 1 % de juros ao mês. Entretanto, ao estabelecer o segundo plano, desejo garantir
para mim uma rentabilidade de 5% ao mês sobre o dinheiro a receber. Pede-se detalhar o
plano da venda à prestação.
Solução:
x
renda 5% ao mês, o que dá uma prestação igual a R, tal que ao
2
vendedor seja indiferente entre os dois planos.
Desejamos, pois, que
Va
(1 + i)n − 1
=
A
i(1 + i) n
20000 =
x
(1 + i) n − 1
x
(1 + 0,05) 24 − 1
x
+A
=
+
A
=
+ A13,7986
2
2
2
i(1 + i) n
0,05(1 + 0,05) 24
x
em prestações iguais a A calculadas a partir de juros de 1 % ao
2
x
(1 + i) n − 1
(1 + 0,01) 24 − 1
= A
=
A
= A21,2435
mês. Para o cliente a conta é:
2
i(1 + i) n
0,01(1 + 0,01) 24
O cliente vai pagar a quantia
28
04/08/09
3:24
Engenharia Econômica
Demétrio E. Baracat
Resolvendo o sistema encontra-se A=570,24/mês ou x= 24249
3.9 EXERCÍCIOS
3.9.1 Pede-se:
a) O Valor Atual de um fluxo uniforme de R$ 5.000,00 durante 12 períodos com taxa de juros
compostos de 7% por período.
b) Valor Final do caso a.
c) Equivalente uniforme anual em 8 períodos para o fluxo do caso a.
d) Repetir o caso a) para uma taxa de juros de 7,17%.
Resposta a) R$ 39713,43 b) R$ 89442,26 c) R$ 6650,72 d) R$ 36356,10
3.10.2 A que taxa de juros compostos anuais deverá ser colocado certo capital para que
triplique ao fim de 10 anos?
Resposta 11,6%a.a.
3.10.3 Determinar a taxa de juros mensal que, composta trimestralmente, seja equivalente a
uma taxa de 8,4% a.m. (composta mensalmente).
Resposta 9,125%
3.10.4 Você mantém o seu capital em um banco de investimentos que paga juros compostos
de 24% a. a. com capitalização trimestral. Calcule o montante de um capital de R$ 100.000,00
aplicado durante 29 meses.
Resposta R$ 175.706,00
3.10.5 Determinada instituição financeira adquiriu do Banco Central, através de leilão, um lote
de Letras do Tesouro Nacional com prazo de resgate em 91 dias, pagando com uma taxa de
deságio de 14%. Qual é o juro simples efetivo a.a. desta operação?
Resposta 64,8%a.a.
3.10.6 Considerados juros de 2% ao mês, qual o valor atual de:
a) uma série de 51 pagamentos mensais consecutivos iguais a R$1.000 cada um vencendo nos
instantes 0, 1,2, . . ., 50
b) uma série de 20 pagamentos mensais consecutivos x, tais que x, = 500 t; t= 1,2,..., 20
29
04/08/09
3:24
Engenharia Econômica
Demétrio E. Baracat
Resposta a) R$ 32423,50
b)R$ 80500,00
3.10.7 Uma firma comprou um equipamento por R$ 10.000,00 de entrada mais um pagamento
R$ 15.000,00 após um ano. Estima-se que o equipamento poderá ser vendido como sucata por
R$ 5.000,00 após 5 anos, e que sua manutenção custará R$ 1 .000,00 por trimestre nos últimos
3 anos. Desejando alugar este equipamento a terceiros, quanto deverá cobrar em parcelas
trimestrais iguais para ter um lucro de 25% sobre o valor atual do custo? Considerar receitas e
pagamentos no fim dos períodos e juros de 5% ao tri mestre.
Resposta R$ 3654,00
3.10.8 Uma firma transportadora compra caminhões por R$ 110.000 e incorre em custos
anuais de manutenção de R$ 10.000 no primeiro ano, R$ 12.000 no segundo e assim por
diante, aumentando sempre à razão de R$ 2.000 por ano. Um caminhão com cinco anos de
uso pode ser vendido por R$ 40.000 e um com seis por R$30.000. O custo de oportunidade do
capital é de 10% a. a. Calcule os EUA de cinco e de seis anos de uso do caminhão. Decida se é
melhor ficar com o caminhão durante cinco ou durante seis anos antes de trocar.
Resposta a) R$ 36086,00
b)R$ 35808,00
melhor 6 anos
3.10.9 Uma loja anuncia um carro segundo dois planos alternativos de venda:
1° plano: R$ 10.000,00 de entrada mais R$ 25.000;00 após 3 meses, mais R$ 25.000,00 após 7
meses.
2.° plano: R$ .25.000,00 de entrada mais R$ 40.000,00 depois de um ano.
Qual o valor a vista do carro? Observe que na solução aparecerão duas raízes, das quais apenas
uma faz sentido do ponto de vista econômico.
Resposta R$ 53450,00
3.10.10 Qual deve ser a taxa anual do custo de oportunidade do capital para minha firma para
que seja indiferente alugar uma máquina por 10 anos pagando um aluguel de 20 mil reais por
ano (no fim de cada ano) ou comprar esta máquina pagando 50 mil reais no início do primeiro
ano, 25 mil no início do segundo e 25 mil no início do terceiro ano?
O valor residual da máquina ao fim de 10 anos de uso é nulo.
Resposta 18,3%
3.10.11 Meu consumo anual de fandangos especiais é de 5.000 peças. Posso comprá-los
prontos a R$ 100 por unidade ou fabricá-los a um custo variável unitário de R$ 60. Para
fabricá-los preciso comprar uma máquina fandangadeira especializada por R$ 1.500.000, que
trabalhará durante dez anos antes de ser jogada fora sem valor residual. Suponha que o custo
do capital para minha firma é de 15%. a.a.
30
04/08/09
3:24
Engenharia Econômica
Demétrio E. Baracat
a) Decida entre comprar pronto ou pela fabricação própria.
b) Supondo que já tenha sido anteriormente comprada uma fandangadeira especializada, que
vai durar mais cinco anos, e que não haja mercado de segunda mão para este tipo de máquina,
repita o tem anterior.
c) Nas condições do item a, calcule o Ponto de Equilíbrio no consumo de fandangos para a
mudança da decisão.
Resposta a) Compra pronto
b)Fabrica
c) R$ 7472,00
3.10.12 A firma Inducapacitoresistor desenvolveu um instrumento automático para monitorar
a pressão sanguínea de pacientes num hospital. O setor de vendas avaliou o potencial do
mercado e concluiu que poderiam vender cerca de 400 instrumentos no primeiro ano, e, a
seguir, aumentar as vendas em 50 instrumentos cada ano até o máximo de seis anos. Após este
ano, a competição forçará a elaboração de outro projeto inteiramente novo, O setor de
produção estudou o projeto do instrumento as previsões de venda. Chegou-se, então, a dois
possíveis métodos de produção, um mais intensivo em mão-de-obra que o outro.
O método A requer um investimento inicial de R$ 300.000 em ferramentas e cerca de R$
75.000 em mão-de-obra e material no primeiro ano. A mão-de-obra e o material vão aumentar
em aproximadamente R$ 5.000 cada ano (isto é, R$ 80.000,00 no segundo ano, e assim por
diante). No fim do período de seis anos, as ferramentas terão um valor residual de R$ 20.000.
O método B requer um investimento inicial de R$ 500.000. Custos de mão-de-obra e material
R$ 60.000 para o primeiro ano, com um aumento de R$ 2.500 por ano. Ao fim dos seis anos, o
valor residual das ferramentas e equipamentos será de aproximada mente R$ 150.000.
Se o método B for o escolhido, o imposto de renda, adicional a se pagar em relação ao método
A, será de R$ 5.800, e aumentará aproximadamente R$ 750 cada ano. Considere o Imposto de
Renda como custo adicional.
A firma considera a rentabilidade mínima aceitável de i = 10% para o capital, após o imposto
de renda. A renda bruta (oriunda das vendas) não será afetada pela escolha no método de
produção.
Aproveitamos a ocasião para mostrar que o imposto de renda pode afetar decisões. No
presente problema, ele tão somente entra como custo adicional.
a) Calcule o valor atual dos custos dos seis anos de produção pelos métodos A e B.
b) Calcule os correspondentes equivalentes uniformes anuais (EUA);
Resposta
a) VaA=R$ 663702,00 VaB=R$ 733332,00
b) AA=R$152389,00
AB=R$ 168377,00
3. 10.13 A firma Trambolhos & Cia. precisa aumentar sua produção de uma pecinha de
altíssima precisão. Depois de muita análise, concluiu-se que, tecnicamente, isto poderia ser
31
04/08/09
3:24
Engenharia Econômica
Demétrio E. Baracat
feito por uma máquina MAXTREPIDA operada manualmente ou um máquina
SUPERTREPIDAMAX operada por meio de controle remoto sem fio. A capacidade de
produção de ambas as máquinas é praticamente a mesma.
A máquina MAXTREPIDA custa aproximadamente R$ 150.000, uma vida útil de 20 anos e
um valor residual de R$ 25.000. Os gastos anuais de manutenção e energia serão da ordem de
R$ 25.000, e para operação pagar-se-ão R$ 40.000 em salários e horas extras. Será necessário
efetuar reforma de maior porte ao fim do quinto, do décimo e do décimo quinto anos de
operação a um custo de R$ 30.000 cada vez.
A máquina SUPERTREPIDAMAX é composta de duas unidades: a unidade básica e a
controle remoto sem fio. A máquina básica custa R$ 250.000, tem uma vida útil de 20 anos e
um valor residual estimado em R$ 40.000. O custo de energia e manutenção é de R$ 35.000,enquanto a operação sai R$ 55.000 anuais. A máquina necessitará de reformas no quinto, no
décimo e no décimo quinto anos a um custo de R$ 20.000 cada vez. A unidade de controle
remoto sem fio por conter leds com rubis custa aproximadamente R$ 125.000, e tem uma vida
útil de dez. anos, com valor residual de R$ 25.000. Os gastos anuais em energia e manutenção
são de R$ 27.500.
Comprando a máquina MAXTREPIDA, resultará num aumento de imposto de renda de R$
1.500 anuais, em relação à compra da máquina SUPERTREPIDAMAX.
A taxa de retorno mínima aceitável para a firma, após o imposto de renda, é de i 10%.
a) Calcule o equivalente uniforme anual da compra de duas máquinas SUPERTREPIDAMAX.
b) Qual o EUA da compra de uma máquina MAXTREPIDA?
c) Calcule o valor atual de custo de 20 anos de serviços de uma máquina.
SUPERTREPIDAMAX e de uma máquina MAXTREPIDA.
Resposta
a) R$ 173145,00 b) R$ 169367,00
c) VaMAXTREPIDA= R$737044,00
VaSUPERTREPIDAMAX= R$1441,92
32
04/08/09
3:24