Prova_final_matematica6_1chamada_2014_Doc-Manuela 09/07/14 17:17 Page 1
Proposta de resolução da Prova Final de Matemática
2.o Ciclo do Ensino Básico
Prova 61/1.a Fase/2014
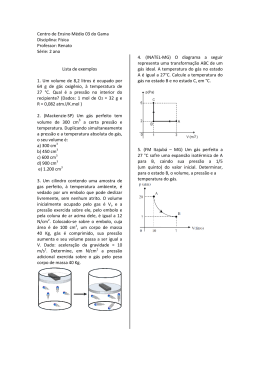
Caderno 1
1.
O preço médio, em euros, que o pai do Américo pagou por litro de azeite é de 3,76€.
3,60 + 4,75 + 3,98 + 17,75
30,08
ᎏᎏᎏᎏᎏᎏ = ᎏ = 3,76 euros
8
8
2.
13
A resposta é ᎏ
1050
M105 = {105, 210, 315, 420, 525, 630, 735, 840, 945, 1050, …}
M350 = {350, 700, 1050, …}
m.m.c. (105, 350) = 1050
ou
105
35
7
1
3
5
7
350
175
35
7
1
2
5
5
7
105 = 3 ¥ 5 ¥ 7
350 = 2 ¥ 52 ¥ 7
m.m.c. (105, 350) = 2 ¥ 3 ¥ 52 ¥ 7 = 1050
10
3
13
1
1
ᎏ+ᎏ=ᎏ+ᎏ= ᎏ
1050
1050
1050
105
350
(¥ 10)
(¥ 3)
3.
O volume da peça é aproximadamente 10081 cm3.
Volume do cilindro = 3,1416 ¥ (11,8)2 ¥ 22,5 = 9842,31864 cm3
Volume do cubo = 6,2 ¥ 6,2 ¥ 6,2 = 238,328 cm3
Volume da peça = 9842,31864 + 238,328 = 10080,64664  10081 cm3
4.
A área, em cm2, da porção de cartolina que sobrará depois de o Duarte recortar o círculo é 1515,8 cm2.
O diâmetro do círculo é igual à largura do retângulo.
49,5
Raio do círculo = ᎏ = 24,75 cm
2
Área do círculo = 3,1416 ¥ (24,75)2 = 1924,42635 cm2
Área do retângulo = 69,5 ¥ 49,5 = 3440,25 cm2
Área da porção de cartolina que sobra = 3440,25 – 1924,42635 = 1515,82365  1515,8 cm2
5.
O preço de venda de cada frasco de mel é de 7,54€.
286 ¥ 0,45 = 128,7 (valor do aumento no total de frascos comprados)
286 + 128,7 = 414,7 (preço dos 55 frascos com 45% de aumento)
414,7  55 = 7,54 (preço de venda de cada frasco de mel)
© Texto
Prova_final_matematica6_1chamada_2014_Doc-Manuela 09/07/14 17:17 Page 2
Caderno 2
6.
A opção correta é F.
7.
As letras que têm simetria de rotação são as letras I, S, O.
8.
36  12 = 3
7,5  3 = 2,5
O número representado pelo símbolo é 2,5.
9.
As medidas dos comprimentos dos lados é 11 cm, 12 cm e 13 cm.
A medida do comprimento, em centímetros, do lado maior é 13 cm.
10.
A opção que pode representar o valor correto obtido pelo Jorge é 600.
11.
5
1
8 – ᎏᎏ ¥ 6 + ᎏᎏ =
4
3
30
1
8
=ᎏ–ᎏ+ᎏ=
1
4
3
(¥ 12)
(¥ 3)
(¥ 4)
96
90
4
= ᎏ – ᎏ + ᎏ =
12
12
12
10
5
= ᎏ = ᎏ
12
6
12.
O nome do polígono representado na Figura 3 é octógono.
13.
Por ordem crescente: 3,06 < 3,065 < 3,56 < 3,6.
14.
2 5
O inverso de ᎏᎏ é ᎏᎏ.
5 2
5
ᎏᎏ = 5  2 = 2,5
2
2
A opção que representa o inverso de ᎏᎏ é 2,5.
5
15.
A medida da área da região sombreada é a opção 11.
16.
2
2
=ᎏ+ᎏ=
3
5
(¥ 5)
(¥ 3)
10
6
= ᎏ + ᎏ =
15
15
16
= ᎏ >1
15
16
A mãe da Luciana tem razão, pois ᎏ representa um número maior do que a unidade. Logo, a Luciana gastou mais
15
dinheiro do que aquele que tinha.
© Texto
Prova_final_matematica6_1chamada_2014_Doc-Manuela 09/07/14 17:17 Page 3
17.
A opção que representa uma potência equivalente a 38 : 32 é 36.
18.
A largura, em centímetros, da planta desenhada pelo Gustavo é 9 cm.
c = 5 m = 500 cm
l = 3 m = 300 cm
500
300
ᎏ = ᎏ
15
x
15 ¥ 300
x = ᎏᎏ
500
x=9
ou
15 ––––––––––––– 5
x ––––––––––––– 3
x
15
ᎏ = ᎏ
3
5
15 ¥ 3
x = ᎏᎏ
5
x=9
19.
C
α = 100˚
β = 45˚
A
20.
8 cm
B
Preparar a Prova Final 6.o ano Matamética
20.1
dt_01_PFMat62014 · 1prova · FR
2
3
4
5
8
7
1 1 5 9
0 2 3 5 5 7 7 8
0 0 0 5 6 6
4
20.2
Três alunos em 20 leram exatamente 50 páginas durante o fim de semana.
3
ᎏ = 3  20 = 0,15
20
A opção que indica a frequência relativa dos alunos que leram exatamente 50 páginas durante o fim de semana
é 15%.
© Texto
Prova_final_matematica6_1chamada_2014_Doc-Manuela 09/07/14 17:17 Page 4
21.
180 – (56 + 60) = 64
A ângulos com amplitudes diferentes opõem-se lados com medidas de comprimento diferentes.
Esse triângulo quanto aos lados é classificado de escaleno.
22.
Se tivesse comprado bilhete simples para todas as viagens efetuadas durante esse mês, a Maria teria gasto a
mais 11,65€.
0,90 ¥ 40 = 36
36 – 24,35 = 11,65
23.
São 12 os seus vértices.
Preparar a Prova Final 6.o ano Matamética
dt_02_PFMat62014 · 1prova · FR
24.
1
2
8
3
7
4
6
72  8 = 9
5
Preparar a Prova Final 6.o ano Matamética
A opção que apresenta
a largura constante
dt_03_PFMat62014
· 1prova ·da
FRmoldura cinzenta é 9 cm.
FIM
© Texto