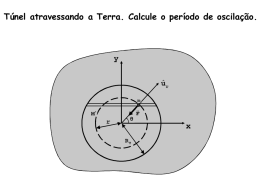
4ª LISTA DE EXERCÍCIOS – POTENCIAL ELÉTRICO
1. As condições típicas relativas a um relâmpago são aproximadamente as seguintes: (a)
Diferença de potencial entre os pontos de descarga igual a 109 V; (b) Carga total
transferida igual a 30 C. Que quantidade de gelo a 0º C seria possível derreter se toda
energia liberada pudesse ser usada para esse fim?
Resposta: 99 toneladas
2. Um núcleo de ouro contém uma carga positiva igual a de 79 prótons. Uma partícula j
(Z=2) é projetada diretamente sobre o núcleo, de um ponto muito afastado deste, com
uma energia cinética igual a K. A partícula chega exatamente a tocar a superfície do
núcleo (suposto esférico), antes de ser repelida na mesma direção de incidência. (a)
Calcule o valor de K, supondo o raio do núcleo igual a 5 × 10-15 m. (b) As partículas j
utilizadas nas experiências de Rutherford e seus colaboradores tinha uma energia igual a
5 MeV. Que se pode concluir daí?
Resposta: (a) 45 MeV; (b) As partículas α se aproximavam dos núcleos de ouro, sem,
contudo, “tocá-los”
3. (a) Qual a diferença de potencial necessária para acelerar um elétron, de acordo com a
Mecânica Newtoniana, até a velocidade da luz? (b) A Mecânica Newtoniana é incorreta
para velocidades próximas à da luz, e a expressão relativística para a energia cinética (no
lugar de K = ½ mv²) é


1
K = m c2 
− 1
2 2 12

 1 − v c
(
)
Calcule, então, a velocidade realmente adquirida pelo elétron ao ser acelerado pela
diferença de potencial calculada no item (a). (c) A que fração da velocidade da luz
corresponde o resultado do item (b)?
Resposta: (a) ∆V = 2,6 × 105 V; (b) v = 2,238 × 108 m/s; (c) v = 0,75 c
4. A densidade de carga de uma superfície plana é σ = 10-7 C/m². Qual é a separação entre
duas superfícies eqüipotenciais correspondentes a uma diferença de potencial de 5,0 V?
Resposta: 0,89 mm
5. Duas placas condutoras grandes, paralelas entre si, e separadas por uma distância de 10
cm, têm cargas iguais e de sinais opostos nas faces que se confrontam. Um elétron
colocado a meia distância entre as duas placas experimenta uma força de 1,6 × 10-15 N.
Qual é a diferença de potencial entre as placas?
Resposta: E = 1 × 104 V/m; ∆V = 1000 Volts
6. Na experiência da gota de óleo, de Millikan (Fig. 1), mantém-se um campo elétrico de
1,92 × 105 N/C entre as duas placas separadas de 1,50 cm. Calcule a diferença de
potencial entre as placas.
Resposta: 2900 Volts
7. Seja uma carga puntiforme q = 1,5 × 10-8 C. (a) Qual é o raio da superfície eqüipotencial
correspondente a 30 V? (b) Serão igualmente espaçadas (no sentido radial) as superfícies
cujos potenciais diferem sucessivamente por uma parcela fixa (por exemplo 1 V)?
Resposta: (a) r = 4,5 m; (b) Não, pois o potencial varia com o inverso da distância
8. Seja uma carga puntiforme q = 10-6 C. Considere os pontos diametralmente opostos A e
B, distantes de q, respectivamente, 2 e 1 m, como mostra a Fig. 2-a. (a) Qual o valor da
diferença de potencial VA – VB? (b) Repita o cálculo para os pontos A e B da Fig. 2-b.
Resposta: (a) –4500 V;
escalar
(b) O mesmo que (a), porque o potencial é uma quantidade
9. Localize, na Fig. 3, os pontos (a) onde V = 0 e (b) onde E = 0. Considere apenas os
pontos da reta que une as cargas e suponha que d = 1 m.
Resposta: (a) x1 = 25 cm; x2 = -50 cm; (b) x3 = 1,40 m
10. Desenhe aproximadamente (a) as linhas de força e (b) as interseções das superfícies
eqüipotenciais com o plano da figura, para a situação apresentada no Exercício 9.
(Sugestão: Considere, primeiramente, o comportamento do campo nos pontos próximos
de cada uma das cargas e nos pontos muito distantes do par de cargas.)
11. Obtenha uma expressão para VA – VB na situação descrita pela Fig. 4. Verifique se o seu
resultado reduz-se aos valores esperados quando d = 0 e quando q = 0.
Resposta: VA − VB =
qQ
1
2 π ε 0 a (a + d )
12. Mostre que V(r), supondo r >> a, para pontos situados no eixo vertical da Fig. 5, vale:
V=
1
4 π ε0
 q 2a q 
 +

r2 
r
Seria possível prever este resultado antecipadamente? (Sugestão: Este sistema de cargas
pode ser considerado como a superposição de uma carga isolada e um dipolo.)
13. Uma partícula de massa m, carga q > 0 e energia cinética inicial K é projetada (do
“infinito”) na direção de um núcleo pesado de carga Q, o qual ocupa uma posição fixa no
nosso referencial. (a) Se a “pontaria” for “perfeita”, a que distância do centro do núcleo
estará a partícula quando atingir instantaneamente o repouso? (b) Com uma pontaria
imperfeita, a distância mais próxima do núcleo foi igual ao dobro da atingida no item (a).
Determine a velocidade da partícula para essa distância mínima.
Resposta: (a) qQ / 4πε0K; (b) K / m
14. Obtenha uma expressão para o trabalho necessário para juntar as quatro cargas na forma
mostrada na Fig. 6.
Resposta: -0,21 q²/ε0a
15. Qual a energia potencial elétrica do sistema de cargas da Fig. 7? Suponha que q1 = +1,0
× 10-8 C, q2 = -2,0 × 10-8 C, q3 = +3,0 × 10-8 C, q4 = +2,0 × 10-8 C e a = 1,0 m.
Resposta: -6,4 × 10-7 J
16. Duas cargas q (= +2 × 10-6 C) estão fixas no espaço e separadas pela distância d (= 2
cm), como está indicado na Fig. 8. (a) Qual é o potencial elétrico no ponto C? (b) Traga
uma terceira carga q (= +2 × 10-6 C) muito lentamente do infinito até C. Quanto trabalho
terá de efetuar? (c) Qual é a energia potencial U da configuração, quando a terceira carga
se encontra no ponto desejado?
Resposta: (a) 2,5 × 106 V; (b) 5,1 J; (c) 6,9 J
17. Dois elétrons estão separados por uma distância de 2 m. Um terceiro elétron é projetado
do infinito e atinge o repouso a meia distância entre os outros dois. Qual deve ser sua
velocidade inicial?
Resposta: 32 m/s
18. Uma partícula de carga (positiva) Q está fixa num ponto P. Uma segunda partícula de
massa m e carga (negativa) –q move-se a velocidade constante num círculo de raio r1,
centrado em P. Derive uma expressão para o trabalho W que deve ser efetuado por um
agente externo sobre a segunda partícula, de modo a aumentar até r2 o raio do círculo de
movimento centrado em P.
qQ  1 1 
Resposta: W =
 − 
8 π ε 0  r1 r2 
19. Descubra uma maneira de dispor três cargas puntiformes, separadas por distâncias
finitas, de modo que a energia potencial seja igual a zero.
20. O potencial elétrico varia ao longo do eixo dos x, como mostra o gráfico da Fig. 9. Para
cada um dos intervalos mostrados (ignorar o efeito relativo aos pontos extremos dos
intervalos), determinar a componente x do campo elétrico e representar Ex em função de
x.
Resposta: EXab = -6 V/m;EXbc = 0;EXcde = 3 V/m;EXef = 15 V/m;EXfg = 0;EXgh = -3 V/m
1
dq
, que o
∫
4 π ε0 r
potencial num ponto do eixo de um anel carregado de raio a é dado por
21. (a) Mostre, calculando diretamente a partir da equação V = ∫ dV =
V=
1
4 π ε0
q
x2 + a2
(b) A partir deste resultado, obtenha a expressão correspondente para E.
qx
1
Resposta: (b) E x =
4 π ε0 x 2 + a 2 3 2
(
)
22. Vimos que o potencial num ponto do eixo de um disco carregado é dado por
V=
σ  2
r + a 2 − r


2 ε0 
Mostre, partindo da expressão acima, que o valor de E, nos mesmos pontos, vale
E=
σ
2 ε0
1− r
r2 + a2
Reduz-se esta expressão de E a algum valor esperado quando (a) r >> a e (b) r << a?
Resposta: (a) E = 0; (b) E = r/2ε0
23. Qual é a densidade de carga σ sobre a superfície de uma esfera condutora de raio 0,15 m,
cujo potencial é de 200 V?
Resposta: 1,2 × 10-8 C/m²
24. Se a Terra tivesse uma carga total correspondente à de uma distribuição equivalente a 1
elétron/m² de sua superfície (uma suposição muito artificial), (a) qual seria o potencial da
Terra? (b) Qual seria o campo elétrico nos pontos exteriores vizinhos à sua superfície?
Resposta: (a) V = -0,12 V; (b) E = 1,8 × 10-8 N/C, radialmente para dentro
25. Pode-se produzir uma carga de 10-8 C simplesmente por atrito. A que potencial esta
carga elevaria uma esfera de 10 cm de raio?
Resposta: 900 V
26. Considere uma camada esférica fina, condutora e isolada, que se encontra carregada
uniformemente com densidade de carga constante σ (C/m²). Determine o trabalho
necessário para deslocar uma pequena carga positiva de prova q0 (a) da superfície da
camada para o seu interior, através de um pequeno orifício; (b) de um ponto na superfície
até outro, qualquer que seja a trajetória; (c) de ponto para ponto dentro da camada; (d) de
um ponto arbitrário P fora da camada, ao longo de qualquer trajetória, que pode ou não
atravessar a camada, até o ponto P de volta; (e) nas condições do problema, importa se a
camada é ou não condutora?
Respostas: (a) Zero; (b) Zero; (c) Zero; (d) Zero; (e) Não
27. Duas esferas condutoras idênticas, de raio r = 0,15 m encontram-se separadas pela
distância a = 10 m. Qual a carga sobre cada esfera, se o potencial de uma delas é de
+1500 V e o da outra é de –1500 V?
Resposta: ± 2,5 × 10-8 C
28. Duas esferas condutoras idênticas, uma de 6 cm de raio e a outra de 12 cm de raio, cada
qual com carga de 3 × 10-8 C, estão bem distantes uma da outra. Se as esferas são ligadas
por um fio condutor, determinar (a) o sentido do movimento e a intensidade da carga
transferida e (b) a carga final sobre cada esfera e o potencial de cada uma delas.
29. Seja R1 = 1 cm e R2 = 2 cm na Fig. 10. Antes das esferas serem ligadas pelo fio fino, a
menor tinha uma carga de 2 × 10-7 C, enquanto que a maior estava descarregada. Calcule,
para cada esfera, (a) a carga, (b) a densidade de carga e (c) o potencial, após a ligação ser
estabelecida.
Resposta: (a) q1 = 0,67 × 10-7 C; q2 = 1,33 × 10-7 C
(b) σ1 = 2,1 × 10-4 C/m²; σ2 = 2,6 × 10-5 C/m²
(c) V1 = V2 = 6 × 104 V
30. (a) Uma gota d’água esférica tem uma carga de 3 × 10-11 C, e o potencial na sua
superfície é de 500 V. Qual é o raio da gota? (b) Se duas gotas iguais a essa, com a
mesma carga e o mesmo raio, se juntarem para constituir uma única gota esférica, qual
será o valor do potencial na superfície da nova gota assim formada?
Resposta: (a) r = 0,54 mm; (b) V’ = 794 V
31. (a) Qual a quantidade de carga necessária para elevar uma esfera metálica, isolada, de 1
m de raio, ao potencial de 106 V? Repita o cálculo para uma esfera de 1 cm de raio. (b)
Qual a razão para o uso de uma esfera grande num gerador eletrostático, quando o
mesmo potencial pode ser atingido, com menor quantidade de carga, usando-se uma
esfera pequena?
Resposta: (a) 1,1 × 10-4 C; 1,1 × 10-6 C; (b) Devido ao maior campo E na superfície da
menor esfera
32. Uma partícula a é acelerada, num gerador eletrostático, pela diferença de potencial de
um milhão de Volts. (a) Qual a energia cinética que ela adquire? (b) Que energia cinética
teria um próton nas mesmas circunstâncias? (c) Qual das duas partículas atinge a
velocidade maior, aceleradas ambas a partir do repouso?
33. A diferença de potencial entre a superfície armazenadora de cargas de um gerador
eletrostático, e o local onde elas são depositadas na correia rolante é de 3 × 106 V. Se esta
transporta cargas a razão de 3 × 10-3 C/s, qual a potência necessária para acionar a
correia, considerando-se apenas as forças elétricas?
Resposta: R = 9,0 kW