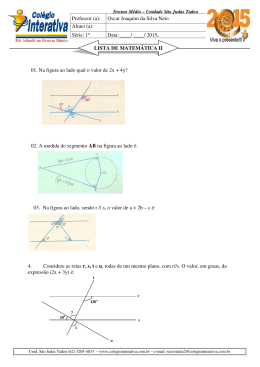
Escola Secundária com 3º ciclo D. Dinis
11º Ano de Matemática – A
Tema I – Geometria no Plano e no Espaço II
Aula nº 4 do plano de trabalho nº 2
Resolver a tarefa da página 54.
“Razões trigonométricas exactas no círculo trigonométrico”
1. Nos círculos trigonométricos da figura estão representados vários ângulos que se obtêm a
partir da divisão da circunferência em 8 (à esquerda) e 12 (à direita) partes iguais.
π
3π
π
π
2π
π
rad
2
π
rad
4
rad
π
2
rad
rad
4
5π
π
π
rad
6
π rad
4
rad
3π
π
7π
π
0 rad
rad
11π
π
6
4π
π
rad
4
rad
rad
6
π rad
0 rad
7π
π
5π
π
rad
3
3
2
rad
3
3π
π
2
rad
6
rad
5π
π
rad
3
Comecemos por ler os ângulos marcados nos círculos:
No da esquerda temos quatro ângulos:
um no 1º quadrante de
π
4
radianos.
3π
radianos.
4
4
π 5π
Um no 3º quadrante de π + =
radianos.
4
4
π 7π
Um no 4º quadrante de 2π − =
radianos.
4
4
No da direita temos oito ângulos:
Um no 2º quadrante de π −
dois no 1º quadrante de
π
6
π
=
radianos e de
3
radianos.
5π
π 2π
radianos e de π − =
radianos.
6
6
3
3
π 7π
π 4π
dois no 3º quadrante de π + =
radianos e de π + =
radianos.
6
6
3
3
π 11π
π 5π
dois no 4º quadrante de 2π − =
radianos e de 2π − =
radianos
6
6
3
3
Em cada um dos círculos marcámos também os quatro ângulos que separam os quadrantes
π
3π
rad .
respectivamente 0 ou 2π rad; rad; π rad e
2
2
dois no 2º quadrante de π −
Professora: Rosa Canelas
π
π
=
1
Ano Lectivo 2010/2011
Podemos agora, com base nos valores já conhecidos das razões trigonométricas exactas de
π π
,
e
π
rad , preencher a tabela seguinte:
6 4 3
ângulo (rad) seno Co-seno tangente
0
0
1
0
π
1
3
3
6
2
2
3
π
2
2
1
4
2
2
π
1
3
3
3
2
2
π
2
2π
3
3π
4
5π
6
1
3
2
2
2
1
2
0
−
1
2
2
2
3
−
2
ângulo (rad)
π
7π
6
5π
4
4π
3
3π
2
5π
3
7π
4
11π
6
2π
nd
− 3
−
-1
−
3
3
seno
0
1
−
2
2
2
3
−
2
−
Co-seno tangente
-1
0
3
3
−
2
3
2
1
−
2
1
−
3
2
-1
0
nd
3
2
2
−
2
1
−
2
0
1
2
− 3
−
2
2
3
2
1
-1
−
3
3
0
2. Com base na tabela vamos dar exemplos de dois ângulos que tenham:
4π
5π
a. Senos iguais:
e
e para eles as tangentes são simétricas e os co-senos
3
3
também são simétricos.
2π
5π
b. Senos simétricos e tangentes iguais:
e
e para eles os co-senos são
3
3
simétricos.
2π
4π
c. Co-senos iguais e senos simétricos:
e
.
3
3
7π
4π
d. O seno de um seja igual ao co-seno do outro e reciprocamente:
e
e para eles
6
3
 1

3
3
as tangentes são inversas uma da outra 
=
ou 3 ×
= 1 .
 3

3
3


3. Para determinarmos as razões trigonométricas exactas dos
seguintes ângulos vamos para cada um deles calcular a
determinação positiva mínima de cada um.
a. A determinação positiva mínima de 990º é 270º que em
3π
radianos dá
e da tabela que acabámos de preencher
2
concluímos que:
 3π

sen ( 990º ) = sen 
rad  = −1;
 2

 3π

cos ( 990º ) = cos 
rad  = 0 e que a tangente não está
 2

definida.
Professora: Rosa Canelas
2
Ano Lectivo 2010/2011
b. A determinação positiva mínima de 2370º é 210º que em
7π
radianos dá
e da tabela que acabámos de preencher
6
concluímos que:
1
 7π

sen ( 2370º ) = sen 
rad  = − ;
6
2


3
 7π

e que
cos ( 2370º ) = cos 
rad  = −
2
 6

3
 7π

.
tg ( 2370º ) = tg 
rad  =
6
3


c. A determinação positiva mínima de
−
7π
6
é obtida
7π
5π
+ 2π =
e da
6
6
tabela que acabámos de preencher concluímos que:
 7π 
 5π
 1
sen  −
= sen 
rad  = ;

 6 
 6
 2
somando a esta 2π e obtém-se: −
 7π
cos  −
 6
 7π
tg  −
 6
3

 5π

 = cos  6 rad  = − 2 e que



3

 5π

 = tg  6 rad  = − 3 .



d. A determinação positiva mínima de
100π
6
vamos obter
100
2π
e concluímos que é
e
6
3
da tabela que acabámos de preencher concluímos que:
2π 
3
 100π 

 2π 
;
sen 
= sen  16π +
= sen 
=



3 
2
 6 

 3 
extraindo a parte inteira de
1
 100π 
 2π

cos 
= cos 
rad  = − e que

2
 6 
 3

 100π 
 2π

tg 
= tg 
rad  = − 3 .

 6 
 3

Professora: Rosa Canelas
3
Ano Lectivo 2010/2011