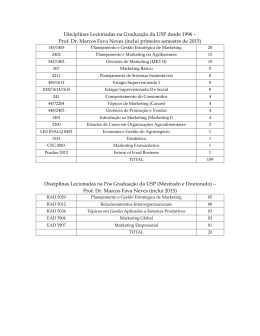
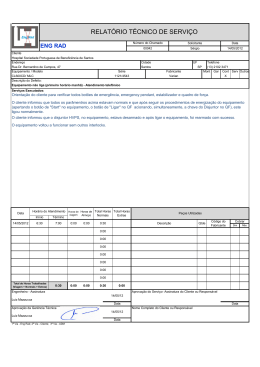
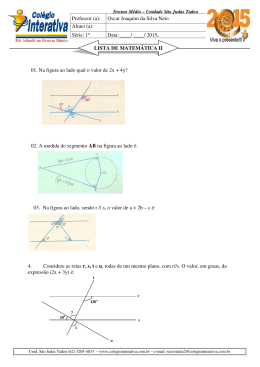
ICMC - USP São Carlos
Prof. R. Nonato
Exercı́cios do Curso Álgebra I - Listas 10
Esta lista é voltada para os alunos da matemática, e interessados em geral,
que querem estudar um pouco mais de álgebra abstrata e/ou estudar no
futuro um curso chamado álgebra comutativa. Boa parte desses exercı́cios
são aplicados nos cursos de álgebra comutativa.
1) Seja f : A → B um epimorfismo de anéis com ker(f ) = K. Mostre que:
a): Se P for um ideal primo em A com K ⊆ P , então f (P ) é um ideal primo em B;
b): Se Q é um ideal primo em B, então f −1 (Q) é um ideal primo em A que contém K.
2) Mostre que Z é um domı́nio de ideais principais.
3) Seja f : A → B um homomorfismo, e A um anel de ideais principais. Mostre que f (A)
é um anél de ideais principais. Ou seja, toda imagem homomórfica de um anel de ideais
principais é um anel de ideais principais.
4) Seja A um anel comutativo. Mostre que o conjunto de todos os elementos nilpotentes
de A forma um ideal em A.
5) Seja A um anel comutativo. Seja I um ideal de A. Defina
Rad(I) = {a ∈ A : am ∈ I para algum m ∈ N ∗ }. Mostre que Rad(I) é um ideal de A.
[Este ideal é chamado o ideal radical do ideal I e bastante explorado nos cursos de
álgebra comutativa].
6) Seja A um anel e a ∈ A um elemento. Mostre que o seguinte conjunto é ideal,
I = {x ∈ A :| x.a = a.x = 0}.
7) Seja A um anel e I um ideal de A. Mostre que A(I) = {a ∈ A | a.x = x.a = 0, ∀x ∈ I}.
8) Seja A um anel e I um ideal de A. Considere o seguinte subconjunto de A,
[A : I] = {a ∈ A : x.a ∈ I, ∀x ∈ A}. Mostre que [A : I] é um ideal que contém I.
Um anel comutativo com identidade é dito um anel local se ele possui
somente um ideal maximal. Por exemplo, um corpo.
9) Seja A um anel comutativo com identidade e I um ideal de A tal que, todo x ∈ A − I
é unidade de A. Então, A é um anel local e I é seu único ideal maximal.
10) Seja A um anel comutativo com identidade 1 e I um ideal maximal de A, tal que 1 + x
é uma unidade em A, para todo x ∈ I. Então A é um anel local.
11) Seja A um anel comutativo. Seja I(resp. J) um ideal de A e Rad(I)(resp. Rad(J))
o ideal radical do ideal I(resp. J). Mostre que:
a): Rad(I) ⊇ I;
b):Rad(Rad(I)) = Rad(I);
c):Rad(I.J) = Rad(I ∩ J) = Rad(I) ∩ Rad(J);
d):Rad(I) = A ⇐⇒ I = A;
d):Rad(I + J) = Rad(Rad(I) + Rad(J));
d):Se I for um ideal primo, então Rad(I n ) = I, para todo n > 0.