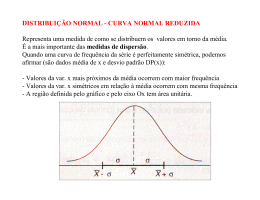
CAPÍTULO 4
Exercícios Resolvidos
R4.1)
Condição para concretização de uma venda
Um certo tipo de componente é vendido em lotes de 1000 itens. O preço de venda do
lote é usualmente de 60 u.m. Um determinado comprador propõe ao vendedor extrair de
cada lote uma amostra com 20 itens; se não houver entre eles nenhum defeituoso, ele
paga 70 u.m. pelo lote; se houver exatamente 1 item defeituoso, ele paga 60 u.m pelo
lote; se houver 2 ou mais itens defeituosos, ele paga 50 u.m pelo lote. Se o vendedor
sabe que em geral cerca de 5% desses itens são defeituosos, ele deverá aceitar ou não
essa proposta?
Solução:
Seja X o número de itens defeituosos na amostra. Então X segue uma lei Binomial com
n = 20 e p = 0,05. Por outro lado, o preço Y a ser pago segundo essa proposta é tal que
 70, se X  0,
o que ocorre com probabilidade 0,95 20  0,358

Y   60, se X  1, o que ocorre com probabilidade 20  0,05  0,9519  0,378
50, se X  2,
o que ocorre com probabilidade 1 - 0,358 - 0,378  0,264

Então E(Y)  70  0,358  60  0,378  50  0,264  60,94 u.m.
Como o preço usual de venda é 60 u.m. por lote, isso mostra que em média a proposta é
ligeiramente vantajosa para o vendedor, embora seja mais sujeita a riscos. Isto porque,
segundo a proposta do comprador, há uma variabilidade envolvida no preço de venda.
R4.2)
Custo de estadia de navios
Estima-se que o custo de estadia de um certo navio que faz transporte de carga,
enquanto está parado em um porto, é da ordem de 30 mil dólares por dia. Admita que o
tempo total de permanência desse navio em um determinado porto (incluindo esperas
em filas, manobras para atracar e desatracar, descarga e carregamento, etc) segue uma
lei de probabilidade exponencial com média de 5 dias.
(a) Em quantos por cento das vezes o custo total de estadia é inferior a 200 mil dólares?
(b) Admita agora que quando o tempo total de permanência do navio excede 8 dias a
administração do porto é obrigada a pagar ao transportador uma multa no valor de 100
mil dólares. Nessas condições, qual é em média o custo líquido para o transportador de
cada visita do navio a esse porto?
Solução:
Sejam X o tempo de estadia (em dias), Y o custo de estadia (em milhares de dólares) e
Z o custo líquido de estadia (em milhares de dólares).
Então:


X é Exponencial com parâmetro λ = 1/5 = 0,2
Y = 30X

(a) P(Y<200) = P(30X < 200) = P(X<6,667) = 1 – exp(–0,2 6,667) = 0,736
(b) E(Z) = 30E(X) – 100 P(X > 8) = 30 x 5 – 100 exp(–0,2 8)
= 150 – 100 x 0,201897 = 129,810.
Ou seja, 129.810 dólares.
R4.3)
Transporte de carga
Uma determinada empresa revende cimento ensacado. Como há permanentemente um
grande movimento de entradas e saídas desses sacos de cimento no galpão da empresa,
pode-se considerar que a quantidade de cimento estocada varia segundo uma
distribuição Normal com média de 30 toneladas e desvio padrão de 10 toneladas. Para
levar os sacos de cimento aos consumidores, a empresa utiliza um caminhão capaz de
transportar até 40 toneladas. A demanda por cimento é muito grande e, por isso, tudo o
que o caminhão levar acabará sendo vendido. Assim sendo, o caminhão sempre sai
levando todo o cimento que houver em estoque naquele momento, desde que a sua
carga máxima não seja ultrapassada.
a) Calcule a média e o desvio padrão do peso da carga do caminhão em uma viagem
com destino aos consumidores escolhida ao acaso.
b) Admita agora que a empresa concluiu que não vale a pena o caminhão fazer essa
viagem, se ele não levar uma carga mínima de 20 toneladas de cimento. Então,
quando o caminhão chega vazio ao galpão para ser carregado, se a quantidade de
cimento em estoque naquele momento for insuficiente, a empresa recorre
imediatamente aos seus fornecedores para garantir que o caminhão saia carregando
exatamente essa carga mínima de 20 toneladas de cimento. Como no item (a),
calcule a média e o desvio padrão do peso da carga do caminhão em uma viagem
escolhida ao acaso, sob as novas condições.
c) Que conclusões podem ser extraídas deste exercício?
Obs.: Note que a distribuição de probabilidade da v.a. aqui considerada é em parte
contínua e em parte discreta.
Solução:
a) Seja Y = Estoque de cimento (em toneladas);
Seja X= peso da carga (em toneladas);
Então Y~N(30,102).
Então, X
;
E(X) =
Seja
.
Fazendo
, temos
.
Então,
= 22,82
E(X) = 22,82+ 40
= 29,17 ton.
Var(X) = E(X2) – (E(X))2 =
=
Fazendo novamente
Var(X) =
A integral acima é igual a
.
,
, obtemos:
I2 = 900
= 900Ф(1) +
Aplicando integração por partes a esta última integral I3, com
u = z e dv = z
teremos: du = dz e v =
Daí, I3 =
Portanto,
I2 = 900 Ф(1) +
=
= 1000 Ф(1) –
= 671,97.
Concluindo, Var(X) =
DP(X) =
= 75,11
ton.
b) Seja novamente X=peso da carga (em toneladas);
, onde Y~N(30,102).
Então X
E(X) =
.
A integral acima é
.
Fazendo, mais uma vez,
,
, obtemos
,
porque
é uma função ímpar.
.
E(X) = (20+40)
ton.
Var(X) = E
Aqui, já sabemos que
=
Por outro lado, fazendo novamente
=
,
.
Mas também sabemos, via integração por partes, que
Então,
.
, a integral acima passa a ser:
Então, I5 =
.
Substituindo esses resultados na expressão de Var(X), obtemos então
Var(X) = 100 (
DP(X) =
ton.
c) No item (a), quando foi feito um truncamento superior na distribuição
N(30,102) a partir de 40, como já era esperado, a média (centro de gravidade)
caiu para de 30 para 29,17 e o desvio padrão também caiu de 10 para 8,67. Já no
item (b), quando além desse truncamento superior, foi feito também um
truncamento inferior abaixo de 20, a distribuição voltou a ser simétrica em torno
de 30 e a dispersão (momento de inércia) diminuiu ainda mais. Assim, a média
voltou a ser igual a 30, passando então o desvio padrão para 7,18.
R4.4)
Função Geradora de Momentos
A função geradora de momentos (fgm) de uma v.a. X associa a cada número
real t o valor esperado de etX: MX(t) = E(etX).
a) Mostrar que MX(t) é um mecanismo, como o próprio nome diz, de gerar
momentos de ordem n, E(Xn).
b) Usando a fgm MX(.), recalcular E(X) e Var(X), se X~Bin(n,p).
c) Usando a fgm MX(.), recalcular E(X) e Var(X), se X~N(µ, σ2).
Solução:
a) MX(t) funciona baseada na expansão em série de
:
Como, sob condições adequadas, o valor esperado da soma é a soma dos
valores esperados; e t é uma constante:
Note que a derivada de ordem n de MX(t) aplicada em t=0 resulta em E(Xn) , ou
seja,
Por exemplo, se n =1,
.
,
o que implica que
.
Analogamente, se n = 2,
o que implica que
.
Esta dedução é válida tanto no caso discreto como no caso contínuo.
b) Seja X ~ Bin(n,p).
Então, pelo Binômio de Newton,
Assim,
,
o que implica que MX’(0) = E(X) = np.
Por outro lado,
,
o que implica que
Assim, Var(X) = E(X2) – (E(X))2 =
– n2p2 = np(1–p)
c) Seja X ~ N(µ,σ2).
Usando a transformação z = (x–µ)/σ → x=z σ+ µ → dx = σdz, temos:
Completando o quadrado, temos
Fazendo w =
, dw = dz, obtemos
.
Daí:
sendo:
e
e
, o que implica que
2
2
2
E(X) = µ e Var(X) = σ + µ – µ = σ2.
R4.5)
Energia cinética de uma molécula
No exercício anterior R3.5, vimos que a função de densidade da velocidade absoluta de
uma molécula é dada pela distribuição de Maxwell
, para x > 0
e
f(x) = 0, para x ≤ 0,
sendo α uma constante.
Obtenha a média e a variância da energia cinética dessa molécula (cuja massa é m).
Sugestão: Novamente, faça a mudança de variável
, e use as propriedades da
função gama. Lembre-se também que a energia cinética de um corpo de massa m que se
move a uma velocidade v é dada por (1/2)mv2.
Solução:
Var
Exercícios Propostos
P4.1) Linha de produção
Suspeita-se que o processo de produção de um certo tipo de componente esteja
desregulado. Para decidir sobre a medida a ser adotada para sanar o problema, o
departamento de produção resolveu conduzir um experimento em que 10 componentes
serão sorteados ao acaso da linha de produção. Seja X o número de componentes fora
das especificações entre eles. Se a proporção de componentes fora das especificações na
linha de produção como um todo for de 30%:
a) Qual o valor mais provável de X e qual a sua probabilidade?
b) Admita que:
 Se X 5, será efetuado um gasto total de 1000 reais para aprimorar a qualidade
da produção.
 Se 2 X 4, esse gasto será de 300 reais.
 Se X 1, não será efetuado nenhum gasto.
Qual a média e o desvio padrão do gasto a ser efetuado?
P4.2) Atendimento domiciliar
O número de solicitações de atendimento domiciliar que um fisioterapeuta recebe em
um dia varia segundo uma distribuição de Poisson com parâmetro λ = 4. Se ele cobra
100 reais por cada visita e é capaz de fazer no máximo 6 atendimentos por dia, qual a
média e o desvio padrão da sua receita diária?
P4.3)
A consultoria sobre investimentos revisitada
Considere novamente o Exercício Proposto 4 do Capítulo 2. Admita agora que os
honorários a serem pagos à equipe de consultores importam no total em 80 u.m., e que
cada decisão acertada implica em um ganho de 100 u.m. Qual a melhor opção: contratar
ou não os consultores?
P4.4) Erro de medição
O erro de medição de uma certa grandeza pode ser considerado como uma v.a. com
distribuição Normal de média = 0 e desvio padrão = 10 . Considere uma função de perda que
está associada à falta de precisão nessa medição e é tal que
Perda =
Determine a média e a variância da Perda.
P4.5) Revisitando o diâmetro das porcas
Considere novamente os dados do Exercício P3.5. Suponha que as porcas têm um custo
unitário de fabricação de 50 centavos. Se elas se encontram dentro dos limites de tolerância,
são vendidas a 1,50 reais cada. Caso contrário, são refugadas. Determine o lucro esperado e o
desvio padrão desse lucro. Dê sua opinião sobre a eficiência desse processo.
P4.6)
Uma transformação da Uniforme
Sejam X e Y v.a.’s tais que:

X tem distribuição Uniforme no intervalo [0,1] ;

Y=
e
.
Então é possível provar que Y tem distribuição exponencial com parâmetro λ.
Mostre que, sob essas premissas, de fato temos E(Y) =
e Var(Y) =
conforme preconiza a
teoria do Capítulo 3.
P4.7)
Duração de uma chamada telefônica
A duração de uma chamada telefônica, em minuto, é uma v.a. contínua X com densidade
f(x) = e-X, x>0; f(x)=0 caso contrário. O custo Y da chamada, em reais, é dado por:
Determine o custo esperado de uma chamada.
P4.8)
O raio de uma esfera
O raio de uma esfera é uma v.a. contínua X uniformemente distribuída entre 1,9 e 2,1
centímetros. Encontre a esperança e a variância do volume da esfera.
P4.9)
Demanda por revistas
A procura por uma determinada revista semanal numa banca de jornais segue uma lei de
Poisson com média de 5,2 exemplares por semana. O valor pago pelo jornaleiro ao
fornecedor é de R$15,00 por unidade e o preço de venda para o consumidor é de R$30,00
por unidade, se a venda é feita na semana em que ela foi publicada. Admita que, terminada
a semana, o jornaleiro consegue vender todas as revistas que sobrarem pelo preço de
R$8,00 por unidade. O contrato atual que ele fez com seu fornecedor prevê o recebimento
de 5 unidades por semana. Ocorre que o jornaleiro tem verificado que em várias semanas
ele deixa de vender essa revista, porque o estoque da semana já estava esgotado. Verifique
se, economicamente, é mais vantajoso para o jornaleiro manter a quantidade que consta no
contrato atual de 5 unidades por semana ou se seria melhor aumentá-la. Se for esse o caso,
que quantidade semanal deveria constar no novo contrato? Por que?
Sugestão: Note que as Vendas são apenas uma parte da Demanda. Isto porque quando um
comprador vai até a banca à procura da revista e ela não está disponível, a venda não se
concretiza.
P4.10)
Tarifa para estacionar
Em um determinado estacionamento, quem quiser deixar seu veículo estacionado paga:
R$10,00, pelas 2 primeiras horas
R$2,00, por cada hora adicional até o limite de 6 horas
R$50,00, se ficar mais de 6 horas
João utiliza diariamente esse estacionamento e, cada vez que ele estaciona, o tempo durante
o qual seu carro fica estacionado segue uma lei de probabilidade exponencial com média de
3 horas. Se Y representa o valor da tarifa que ele vai pagar em um certo dia escolhido ao
acaso:
(a) Qual a função de probabilidade de Y?
(b) Faça um gráfico dessa função de probabilidade.
(c) Qual o valor médio diário E(Y) da tarifa que João paga para estacionar?
(d) Qual o desvio padrão DP(Y) da tarifa diária paga por ele?
P4.11)
Re-deduzindo E(X) e Var(X), através de fgm, para diferentes modelos
Usando a definição de fgm dada no Exercício R4.4, mostre para cada um dos seguintes
modelos probabilísticos a função geradora de momentos Use agora a fgm para re-deduzir as
expressões algébricas de E(X) e de Var(X), quando a v.a. X segue:
(a) Poisson com parâmetros λ, para o qual
(b) Uniforme no intervalo [a, b], para o qual
(c) Exponencial com parâmetro λ, para o qual
,t<λ
P4.12)
Coeficiente de Assimetria
Dada uma variável aleatória X, define-se o seu coeficiente de assimetria pela expressão
µ
σ
sendo µ = E(X) e σ = DP(X). É possível provar que:
I. Se = 0, a função de densidade f da v.a. X é simétrica em relação à reta vertical
x = µ, ou seja, f(µ – y) = f(µ + y), para todo y > 0.
II. Se > 0, a função de densidade f da v.a. X é assimétrica para a direita;
III. Se < 0, a função de densidade f da v.a. X é assimétrica para a esquerda.
Sejam U, V e W três v.a.’s tais que:
 A distribuição de probabilidade de U é exponencial com λ = 1;
 V = exp (–U)

W = exp
(a) Obtenha os gráficos das funções de densidade de U, de V e de W.
(b) Calcule o coeficiente de assimetria
correspondente a cada uma dessas três
variáveis.
Sugestão: Use a função Gama.