Parte II
Análise funcional II
120
Capítulo 5
Produto de Operadores. Operadores
inversos
Neste capítulo vamos introduzir a noção de produto de operadores assim como
a de operador invertível. Para tal precisamos recordar algumas noções já introduzidas em Análise Funcional I e não só. A primeira das quais, tem a ver
com o núcleo N(T ) e a imagem (R(T ) de um operador T , cf. Section 4.1. Seja
T : D(T ) ⊂ X −→ Y um operador linear dado. Então temos
N(T ) := {x ∈ D(T )| T x = 0} ⊂ X,
R(T ) := {T x, x ∈ D(T )}.
No Teorema 4.3 vimos que tanto N(T ) como R(T ) são espaços vectoriais. O
operador T : D(T ) ⊂ X −→ Y diz-se injectivo se e só se a diferentes pontos no
domínio correspondem diferentes imagens, simbolicamente se x, y ∈ D(T )
x!y
=⇒
T x ! T y;
(5.1)
ou ainda que imagens iguais correspondem objectos iguais, simbolicamente
T x = Ty
=⇒
x = y.
(5.2)
5.1 Definição e exemplos
Nesta secção vamos definir o produto arbitrário de operadores lineares. Sejam
T : D(T ) ⊂ X −→ Y e U : D(U) ⊂ Y −→ Z dois operadores lineares e M
121
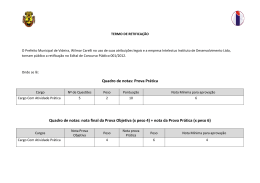
UT
M
BA(M )
T
D(T )
U
A(M )
R(T )
D(U )
R(U )
Figura 5.1: Produto dos operadores T e U.
o maior subconjunto de D(T ) cuja imagem sob T está contido em D(U), isto é,
T (M) ⊂ D(U). De onde resulta que
T (M) = R(T ) ∩ D(U),
ver Figura 5.1.
Definição 5.1 Sejam T : D(T ) ⊂ X −→ Y e U : D(U) ⊂ Y −→ Z dois operadores lineares contínuos tais que R(T ) ⊂ D(U). O produto do operador U pelo
operador T é definido por
UT : D(UT ) ⊂ X −→ Z, x '→ (UT )x := U(T x).
(5.3)
O operador UT definido em (5.3) possui as seguintes propriedades
Proposição 5.2
1. UT é um operador linear,
2. UT é um operador contínuo,
3. temos a seguinte majoração para a norma de UT : (UT ( ≤ (U( (T (.
Prova. Exercício 5.1.
Observação 5.3 O produto de um número arbitrário de operadores lineares contínuos define-se de forma análoga. Para simplificar a notação, vamos supor que
todos os operadores T i , i ∈ {1, . . . , n} são tais que T i ∈ B(X, X). Assim, o produto
T 1 T 2 . . . T n é operador linear contínuo definido por
T 1 T 2 . . . T n : D(T 1 T 2 . . . T n ) ⊂ X → X, x '→ (T 1 T 2 . . . T n )x := T 1 (T 2 (. . . (T n x) . . .)).
122
Em particular se T = T 2 = . . . = T n = T , então temos T T . . . T = T n e a seguinte
majoração para a norma de T n é válida: (T n ( ≤ (T (n .
Proposição 5.4 Sejam T, U, V ∈ B(X, X) operadores lineares contínuos. Então
as seguintes propriedades são verdadeiras:
1. (T U)V = T (UV) (associatividade do produto),
2. (T + U)V = T V + UV (o produto à direita é distributivo em relação à
adição),
3. T (U + V) = T U + T V (o produto à esquerda é distributivo em relação à
adição),
4. α(T U) = T (αV) = (αT )U, para qualquer α ∈ K,
5. se I denotar o operador identidade em X, então IT = T I = T .
Prova. Exercício 5.2.
Decorre desta última proposição que o espaço B(X, X) munido das operações
soma de operadores e produto de operadores lineares contínuos forma um anel
com identidade I, o qual não é comutativo, pois o produto de operadores em geral
não é comutativo. De facto, temos os seguintes contra exemplos.
Exemplo 5.5
1. Sejam X = Y = R2 e os operadores T, U definidos de R2 em
2
R pelas matrizes:
"
!
"
!
0 1
0 −1
.
,
U:
T:
1 0
1 0
Então temos T U ! UT , pois
"
" !
!
1 0
−1 0
= UT.
!
TU =
0 −1
0 1
2. Consideremos X = Y = C([0, 1]) e os operadores T, U definimos de C([0, 1])
em C([0, 1]) por
# 1
(T x)(t) := t
sx(s)ds
0
(U x)(t) := tx(t).
123
Temos
((T U)x)(t) := (T (U x))(t) = t
#
1
s(U x)(s)ds = t
0
#
1
s2 x(s)ds.
0
Por outro lado
((UT )x)(t) := (U(T x))(t) = t(T x)(t) = t
2
#
1
sx(s)ds.
0
Também aqui vemos que T U ! UT .
Vamos de seguida apresentar alguns exemplos de produto de dois operadores
lineares contínuos.
Exemplo 5.6
1. Sejam T, U ∈ B(Rn , Rn ), n ∈ N dois operadores lineares contínuos os quais são definidos em relação às bases canónica (ei )ni=1 , ( f j)nj=1 de
Rn pelas matrizes
T : (ai j )ni, j=1 ,
U : (bi j )ni, j=1 .
Então temos
 n

 n

n
n
n '
'
'
'
 '



 b jk ai j  fi ,
(T U)ek = T (Uek ) = T  b jk f j  =
b jk
ai j f i =


j=1
j=1
i=1
i=1
j=1
e deste modo vemos que a matriz do operador produto T U está associado
ao produto das matrizes de T e U.
2. Consideremos os operadores integrais T, U definimos em C([0, 1]) por
# 1
# 1
(T x)(t) :=
K1 (t, s)x(s)ds,
(U x)(t) :=
K2 (t, s)x(s)ds.
0
0
Então o operador produto T U também é um operador integral. De facto,
temos
# 1
((T U)x)(t) := (T (U x)(t) =
K1 (t, s)(U x)(s)ds
0
# 1
# 1
=
K1 (t, s)
K2 (s, r)x(r)drds
0
0
"
# 1 !# 1
=
K1 (t, s)K2 (s, r)ds x(r)dr,
0
0
124
e neste caso se representarmos por K̃(·, ·) a função definida por
# 1
K̃(t, s) :=
K1 (t, s)K2 (s, r)dr,
0
então T U é um operador integral associado a K̃.
Exercícios
Exercício 5.1 Prove a Proposição 5.2.
Exercício 5.2 Prove a Proposição 5.4.
Exercício 5.3 Considere os operadores lineares contínuos T, U definidos em C([0, 1])
por
(T x)(t) := y(t)x(t),
(U x)(t) := ỹ(t)x(t) y, ỹ ∈ C([0, 1]),
isto é, T (respectivamente U) é o operador de multiplicação por y(t) (respectivamente por ỹ(t)). Prove que o produto T U é o operador de multiplicação por
˜ Calcule a norma de T U.
y(t)y(t).
5.2 Operadores inversos
Nesta secção vamos definir o operador inverso de um operador linear. Já vimos
que o conjunto B(X, X) é um anel com identidade I. Assim, podemos dar a definição de elemento inverso à esquerda (respectivamente inverso à direito) de um
elemento num anel.
Definição 5.7 Seja T ∈ B(X, Y) um operador dado. Então
1. um operador E chama-se inverso à esquerda do operador T se ET = I|D(T )
e neste caso diz-se que T é invertível à esquerda,
2. um operador D chama-se inverso à direita do operador T se T D = I|R(T ) e
neste caso diz-se que T é invertível à direita.
Lema 5.8 Se um operador T tem inverso esquerdo E e inverso direito D, então
os operadores E e D são iguais.
125
Prova. De facto, temos
E = EI = E(T D) = (ET )D = ID = D.
Definição 5.9 (Operador inverso) Um operador linear T diz-se invertível se existem simultaneamente os operadores inverso esquerdo e inverso direito. Neste caso
diz-se que T tem inverso T −1 , isto é, T T −1 = T −1 T = I.
Proposição 5.10 Seja T um operador invertível só à esquerda (respectivamente
só à direita), então o operador inverso esquerdo (respectivamente inverso direito)
não é único.
Prova. Suponhamos que T admite só inverso esquerdo E, isto é, ET = I mas
T E ! I. Consideremos o operador E α , α ∈ K definido por
E α := E + α(I − T E).
Então a família de operadores (E α )α∈K são todos inversos esquerdos de T . Realmente, temos
Eα T =
=
=
=
(E + α(I − T E))T
ET + αT − αT (ET )
I + αT − αT I
I.
Assim, vemos que o inverso esquerdo não é único. Note porém, que se T E = I,
então E α = E, ∀α ∈ K. Daí ser essencial que o operador T tenha unicamente
inverso esquerdo.
A prova para o inverso direito é análoga. Com efeito, se T admite só inverso
direito D, isto é, T D = I mas DT ! I, então a família (Dα )α∈K , onde Dα :=
D + α(I − DT ), são todos inversos direitos de T . Deste modo o inverso direito
também não é único.
Recordemos que uma aplicação f : D( f ) → Y é injectiva se e só se
f (x1 ) = f (x2 )
=⇒
126
x1 = x2 .
(5.4)
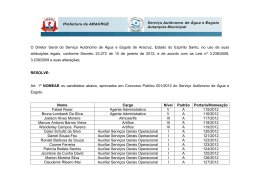
f
X
D(f )
f
−1
R(f )
x
y = f (x)
Y
Figura 5.2: Função inversa.
Neste caso existe a aplicação inversa
f −1 : R( f ) → D( f ), y '→ f −1(y) = x,
onde y = f (x), ver Figura 4.5.
No que toca aos operadores lineares a situação é a seguinte.
Teorema 5.11 Seja T : D(T ) ⊂ X −→ Y um operador linear. Então
1. o operador T é invertível se e só se
Tx = 0
=⇒
x = 0,
(5.5)
ou seja N(T ) = {0}.
2. se o operador inverso T −1 existe, então é linear,
3. se dim D(T ) = n < ∞ e T −1 existe, então dim R(T ) = dim D(T ).
Prova. 1. Suponhamos que T x = 0 implica x = 0 com vista a provar que o
operador inverso T −1 existe, isto é, que o operador T é injectivo. De acordo com
(5.4) temos de provar que T x1 = T x2 implica x1 = x2 . Como T é linear, então
T x1 = T x2 ⇔ T (x1 − x2 ) = 0,
pelo que x1 − x2 = 0 por hipótese. Isto prova que T é invertível.
Inversamente, suponhamos que T é invertível com vista a provar que N(T ) =
{0}, ou seja que T x = 0 implica x = 0. Como T é invertível, então a condição
(5.4) é válida em particular para x2 = 0. Então obtemos
T x1 = T 0 = 0
=⇒
Assim, 1. está provado.
127
x1 = 0.
2. Sejam y1 , y2 ∈ R(T ) dois elementos quaisquer na imagem de T e α, β ∈ K
escalares arbitrários com vista a provar que T −1 é linear, isto é,
T −1 (αy1 + βy2 ) = αT −1 y1 + βT −1 y2 .
Por um lado, como y1 , y2 ∈ R(T ), então existem x1 , x2 ∈ D(T ) tais que
x1 = T −1 y1 ,
x2 = T −1 y2 .
Por outro lado, D(T ) é um espaço vectorial, assim,
αx1 + βx2 ∈ D(T ),
∀α, β ∈ K.
Da linearidade de T decorre que
T (αx1 + βx2 ) = αT x1 + βT x2 = αy1 + βy2 .
Isto implica que
T −1 (αy1 + βy2 ) = αx1 + βx2 = αT −1 y1 + βT −1 y2 ,
o que mostra a linearidade de T −1 .
3. Já vimos, Teorema 4.3-3. que dim R(T ) ≤ dim D(T ). Mas o mesmo teorema
aplicado a T −1 diz-nos que dim D(T ) ≤ dim R(T ). Isto prova que dim R(T ) =
dim D(T ).
Exemplo 5.12 Seja X = Y = Rn e consideremos o operador T ∈ B(Rn , Rn ) associado à matriz (ai j )ni, j=1 . Suponhamos que a condição T x = 0 implica x = 0, isto
é, o sistema homogéneo de equações lineares
n
'
ai j x j = 0,
i = 1, . . . , n,
j=1
possui somente a solução trivial x1 = x2 = . . . = xn = 0. Como é conhecido
da álgebra linear isto é equivalente à invertibilidade da matriz correspondente ao
operador T : (ai j )ni, j=1 . Isto, por sua vez, implica que R(T ) = Rn e, deste modo, T
é um operador invertível, com inverso T −1 , o qual está associado à matriz inversa
de T .
128
Exemplo 5.13 Consideremos agora X = Y = C([0, 1]) e T o operador definido
em C([0, 1]) por
(T x)(t) := x0 (t)x(t),
onde x0 ∈ C([0, 1]) é tal que x0 (t) > 0, ∀t ∈ [0, 1], ou seja, T é o operador de
multiplicação por x0 . Então T satisfaz a condição (5.5) do Teorema 5.11, pois se
T x = 0, então (T x)(t) = 0, ∀t ∈ [0, 1]. Atendendo à definição de T , vem
(T x)(t) = 0 ⇔ x0 (t)x(t) = 0,
como x0 (t) > 0, ∀t ∈ [0, 1], resulta que x(t) = 0, ∀t ∈ [0, 1]. Assim, T é um
operador invertível e o seu inverso T −1 é o operador de multiplicação por x−1
0 . De
facto,
((T T −1 )y)(t) = (T (T −1 y))(t) = x0 (t)(T −1 y)(t) = x0 (t)x−1
0 (t)y(t) = y(t),
−1
−1
−1
−1
((T T )x)(t) = (T (T x))(t) = x0 (t)(T x)(t) = x0 (t)x0 (t)x(t) = x(t).
O domínio de T −1 é R(T ) ⊂ C([0, 1]). Neste caso, temos R(T ) = C([0, 1]), pois se
y ∈ C([0, 1]), então vemos que x−1
0 y ∈ C([0, 1]) é tal que
−1
(T (x−1
0 y))(t) = x0 (t)x0 (t)y(t) = y(t).
Exemplo 5.14 Consideremos o operador T definido por
# t
T : C([0, 1]) → C([0, 1]), x '→ (T x)(t) :=
x(s)ds,
0
t ∈ [0, 1].
Determinar R(T ), verificar a existência de T −1 e no caso de existir T −1 dizer se T −1
é ou não limitado.
Comecemos por encontrar R(T ). Suponhamos que y ∈ R(T ), então existe
x ∈ C([0, 1]) tal que
#
t
y(t) =
x(s)ds.
0
É claro (teorema fundamental do cálculo integral!) que y- (t) = x(t) e assim, se
y ∈ R(T ), então y ∈ C 1 ([0, 1]). Por outro lado, a igualdade y- (t) = x(t) implica
# t
y(t) =
x(s)ds + K,
0
129
onde K é uma constante. Então a constante K terá de ser nula, K = 0. Mas K =
y(0) = 0, assim, R(T ) consiste no espaço vectorial das aplicações y ∈ C 1 ([0, 1])
tais que y(0) = 0. Simbolicamente
+
,
R(T ) := y ∈ C 1 ([0, 1])| y(0) = 0 .
Vamos agora estudar a condição de invertibilidade de T . Então pelo Teorema 5.11 condição (5.5) T será invertível se e só se T x = 0 implica x = 0. Mas
dizer que T x = 0 é dizer que
# t
x(s)ds = 0, ∀t ∈ [0, 1].
0
-t
Suponhamos que x ! 0, então como x é contínua, 0 x(s)ds ! 0, ∀t ∈ [0, 1] o
que contraria o facto de T x = 0. Portanto, podemos concluir que T x = 0 implica
x = 0. Assim, o operador inverso T −1 existe o qual é definido por
T −1 : R(T ) → C([0, 1]), y '→ (T −1 y)(t) := y- (t).
De facto, temos
−1
−1
((T T )y)(t) = (T (T y))(t) =
#
t
−1
(T y)(s)ds =
0
#
t
0
y- (s)ds = y(t) − y(0) = y(t),
−1
e isto prova que T é inverso direito de T . Por outro lado, usando o teorema
fundamental do cálculo integral obtemos que T −1 é inverso esquerdo, de facto
!# ·
"−1
−1
((T T )x)(t) = (T (T x))(t) = (T x) (t) =
x(s)ds (t) = x(t).
0
−1
Finalmente, estudemos o operador T no que respeita à sua limitação. Para
tal consideremos as funções y ∈ C([0, 1]) definidas por
y(t) := tn , n ∈ N.
Temos y ∈ C 1 ([0, 1]) e y(0) = 0 pelo que y ∈ D(T −1 ). A norma de T −1 é dada por
.. −1 ..
.T . = sup |T −1 y|.
|y|=1
Mas a norma em C([0, 1]) é dada por
|T −1 y| = max |(T −1 y)(t)| = max |ntn−1 | = n,
t∈[0,1]
t∈[0,1]
.. ..
.. ..
pelo que .T −1 . = n. Assim, .T −1 . → ∞ quando n → ∞, pelo que T −1 não é
limitado. Notemos, no entanto, que o operador T é limitado com (T ( = 1.
130
Observação 5.15 Uma aplicação muito importante do conceito de operador invertível é a seguinte. Consideremos o operador T : X → X dado, y0 ∈ X um
elemento fixo e a equação (em que x é a incógnita!)
T x = y0 .
(5.6)
Na forma (5.6) podem escrever-se muitos tipos de equações, por exemplo, sistemas de equações lineares, sistemas de equações lineares integrais, sistemas de
equações diferenciais, etc. O problema da existência e unicidade de solução da
equação (5.6) está intimamente lidado ao conceito de operador inverso.
1. Suponhamos que o operador T admite inverso T −1 . Então substituindo x =
T −1 y0 em (5.6) obtemos
T T −1 y0 = Iy0 = y0 ,
pelo que x = T −1 y0 é uma solução da equação (5.6). Neste caso a solução é
única, pois se x̃ é outra solução de (5.6), então
T x̃ = y0
e multiplicando ambos os membros desta igualdade à esquerda por T −1 obtemos
T −1 T x̃ = T −1 y0 ⇔ I x̃ = T −1 y0 ⇔ x̃ = T −1 y0 .
De onde x = x̃ e a solução de (5.6) é única. Neste processo de encontrar
uma solução única de (5.6) usamos as seguintes igualdades
T T −1 = I,
T −1 T = I.
2. Se admitirmos que T só tem inverso direito D, então a solução de (5.6) é
x = Dy0 , pois
T Dy0 = Iy0 = y0 .
No entanto, não podemos provar que a solução x = Dy0 é única, por T não
admitir inverso esquerdo.
3. Pelo contrário, se T admitir inverso esquerdo E, então a existir uma solução
de (5.6) ela é única, pois se x, x̃ são duas soluções, então
T x = y0 ⇒ ET x = Ey0 ⇒ Ix = Ey0 ⇒ x = Ey0
T x̃ = y0 ⇒ ET x̃ = Ey0 ⇒ I x̃ = Ey0 ⇒ x̃ = Ey0 ,
e, assim, x = x̃. No entanto, não sabemos se (5.6) possui ou não solução,
por T não admitir inverso direito.
131
Em forma de conclusão podemos dizer o seguinte:
o operador inverso direito é responsável pela existência de solução da equação T x = y0 enquanto que o operador inverso esquerdo
é responsável pela unicidade desta solução.
Teorema 5.16 Seja X um espaço de Banach e T ∈ B(X, X) um operador linear
limitado dado tal que (T ( = c < 1. Então o operador I − T tem inverso limitado.
O seu inverso (I − T )−1 é dado em termos da série convergente:
(I − T )−1 = I + T + T 2 + T 3 + . . . + T n + . . . .
Prova. Vamos mostrar que a sucessão das somas parciais (S n )∞
n=1 onde
S n = I + T + T2 + T3 + . . . + Tn
é de Cauchy em B(X, X). De facto, se n, m ∈ N tais que m > n, então
.
.
(S m − S n ( = ..T n+1 + T n+2 + . . . + T m ..
.
. .
.
≤ ..T n+1 .. + ..T n+2 .. + . . . + (T m (
≤ (T (n+1 + (T (n+2 + . . . + (T (m
≤ cn+1 + cn+2 + . . . + cm
m
'
=
ck .
k=n+1
Como c < 1, então a série
∞
'
ck
k=1
é convergente, Assim, para todo ε > 0 existe uma ordem N ∈ N tal que se m >
n > N, então
m
'
(S m − S n ( ≤
ck < ε.
k=n+1
(S n )∞
n=1
é uma sucessão de Cauchy em B(X, X). Mas por hipótese, o
Pelo que
espaço X é completo (pois é um espaço de Banach!), então o espaço (B(X, X), (·()
também é espaço de Banach, cf. Teorema 4.13. Portanto, (S n )∞
n=1 é uma sucessão
de Cauchy num espaço de Banach pelo que tem limite S ∈ B(X, X), isto é S =
limn→∞ S n em B(X, X).
132
Vamos agora mostrar que S é o inverso de I − T , isto é, mostrar que S (I − T ) =
(I − T )S = I. De facto, temos
S (I − T ) = lim S n (I − T )
n→∞
= lim (I + T + T 2 + T 3 + . . . + T n − T − T 2 − . . . − T n − T n+1 )
n→∞
= lim (I − T n+1 )
n→∞
= I.
A última igualdade é verdadeira porque
..
. .
.
.I − T n+1 − I .. = ..T n+1 .. ≤ (T (n+1 ≤ cn+1 → 0, n → ∞.
A verificação de que (I − T )S = I é feita de uma forma análoga.
Exercícios
Exercício 5.4 Seja T : X → Y um operador linear invertível e {x1 , . . . , xn } um
subconjunto linearmente independente em D(T ). Mostre que {T x1 , . . . , T xn } é um
subconjunto linearmente independente em R(T ).
Exercício 5.5 Seja X = P([0, 1]) o conjunto de todos os polinómios definidos no
intervalo [0, 1] e T : P([0, 1]) → P([0, 1]) o operador definido por
(T x)(t) := x- (t).
Prove se T é ou não invertível.
Exercício 5.6 Considere o espaço vectorial X de todas as funções reais definidas
em R as quais admitem derivadas de todas as ordens. Seja T : X → X o operador
de derivação em X, isto é,
(T x)(t) := x- (t),
x ∈ D(T ), t ∈ R.
Prove que R(T ) = X mas T −1 não existe.
133
Exercício 5.7 Considere os seguintes operadores T, U definidos em $2 (R) por
T x = (0, x1 , x2 , . . . , xn , . . .),
U x = (x2 , x3 , . . . , xn , . . .),
x = (x1 , x2 , . . . , xn , . . .) ∈ $2 (R),
x = (x1 , x2 , . . . , xn , . . .) ∈ $2 (R).
T chama-se o operador de deslocamento direito e U o operador de deslocamento
esquerdo.
1. Prove que o inverso esquerdo de T é U e deduza que o inverso direito de U
é T.
2. Serão os operadores T, U invertíveis?
Exercício 5.8 Nas condições do Teorema 5.16 mostre que
..
.
.(I − T )−1 .. ≤ (1 − (T ()−1 .
Exercício 5.9 Seja X um espaço de Banach e T ∈ B(X, X) um operador linear
limitado dado tal que (T ( = ε < 1. Mostre que o operador I + T tem inverso
limitado. O seu inverso (I + T )−1 é dado em termos da série convergente:
(I + T )−1 = I − T + T 2 − T 3 + . . . + (−1)n T n + . . . .
Exercício 5.10 Seja T : R2 → R2 o operador associado à matriz
"
!
a b
.
T:
c d
Encontre a condição sobre os coeficientes a, b, c, d tal que o operador T seja invertível. Construa o operador inverso.
Exercício 5.11 Sejam A : X → Y e B : Y → Z dois operadores lineares
bijectivos, onde X, Y, Z são espaços vectoriais. Prove que o operador inverso
(BA)−1 : Z → X existe e a seguinte igualdade tem lugar, cf. Figura 5.3
(BA)−1 = A−1 B−1 .
Exercício 5.12 Seja X um espaço
Banach, T ∈ B(X, X) um operador invertível
.. ..de
−1
−1
e U ∈ B(X, X) tal que (U( < .T . . Mostre que o operador T + U é invertível e
calcule o seu inverso.
Sugestão: Note que T + U pode escrever-se como
T + U = T (I + T −1 U).
Use o Exercício 5.9 para mostrar que I + T −1 U é invertível e o Exercício 5.11 para
calcular o inverso de T + U.
134
BA
X
A
B
Y
Z
(BA)−1
Figura 5.3: Inverso do produto de operadores.
Exercício 5.13 Considere o espaço das sucessões limitadas $∞ (R), isto é
/
0
∞
$ (R) := x = (x1 , x2 , . . . , xn , . . .)| |x|∞ := sup |xi | < ∞ .
i∈N
Em $∞ (R) definimos o operador T por
2
1 x x
xn
3
2
T x = x1 , , , . . . , , . . . ,
2 3
n
x ∈ $∞ (R).
1. Mostre que para qualquer x ∈ $∞ (R), T x ∈ $∞ (R), isto é, T é um operador
de $∞ (R) em $∞ (R). Calcule (T (.
2. Prove que T é invertível mas que o seu inverso T não é limitado.
Exercício 5.14 Seja X = {x ∈ C 1 ([0, 1])| x(0) = 0} e Y = C([0, 1]) dados.
1. Prove que o operador T ∈ B(X, Y) definido por
(T x)(t) := x- (t) − x(t)
é invertível e calcule T −1 .
2. Mostre que o operador U ∈ B(X, Y) definido por
# t
(U x)(t) := x(t) −
x(s)ds
0
é invertível e calcule o seu inverso U −1 .
135