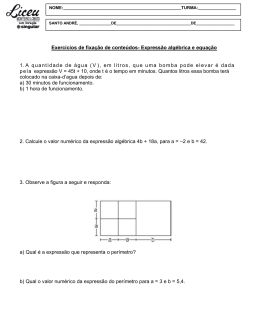
20/07/2015
PROBLEMAS EQUAÇÃO 1º GRAU:
1) Considere o triângulo a seguir, com as medidas indicadas na
figura.
2x - 1
3x + 3
2x + 1
a) Qual a expressão que representa o perímetro do triângulo?
b) Qual o valor correspondente ao perímetro, se x= 5cm?
Respostas:
a) 2x + 1 + 2x - 1 + 3x + 3=
7x + 3
b) Se x=5, temos:
7.5 + 3=
35 + 3
=38 cm
2) Resolva os problemas abaixo usando equação (use x para representar o
número) :
a) O dobro de um número menos 6 resulta 32. Que número é esse?
2x – 6 = 32
R: 19
b) A metade do triplo de um número é igual a 12. Qual o número?
R: 8
1
20/07/2015
c) Quais são os dois números inteiros e consecutivos cuja soma é igual a 31?
e) Qual a medida de cada lado do retângulo, sabendo que o perímetro dele é
igual a 42 cm?
2x + 4
Números: x e x+1
x+2
x + x + 1 = 31
R: os números são 15 e 16
d) Um número tal que o dobro da soma do número com 5 resulta em 40. Que
número é esse?
2. (x + 5) = 40
R: 15
2.(2x + 4) + 2.(x + 2)= 42
x= 5
4x + 8 + 2x + 4= 42
4x + 2x= 42 – 8 - 4
6x= 30
Comprimento: 2.(5) + 4= 14 cm e largura: 5 + 2= 7 cm
f) Rui e Bruno têm, juntos, R$ 1200,00. Se Rui tem R$ 300,00 a mais que Bruno,
quantos reais tem Rui?
Rui: x + 300
Bruno: x
x + x + 300= 1200
R: Bruno 450 reais e Rui 750 reais.
g) José, Raimundo e Pedro pescaram 40 peixes, sendo que Raimundo
pescou dois terços da quantidade pescada por José, e este pescou 8 peixes
a menos que Pedro. Quantos peixes cada um pescou?
R: José pescou 12 peixes, Pedro 20 peixes e Raimundo 8 peixes.
h) Dois ciclistas percorrem juntos 6 km. Sabendo que um percorreu o quádruplo
do outro, quantos metros percorreu cada ciclista?
j) Um avô repartiu entre seus três netos a quantia de R$ 465,00. O neto mais
velho recebeu R $ 30,00 a mais que o neto mais novo, e o neto do meio
recebeu R$ 15,00 a mais que o neto mais novo. Quanto cada neto recebeu?
R: o mais velho 170 reais, o do meio 155 reais e o mais novo 140 reais.
k) O perímetro de um retângulo mede 74 cm. Quais são suas medidas, sabendose que o comprimento tem cinco centímetros a mais que a largura?
R: 1200 m e 4800 m
i) Num estacionamento, entre carros e motos, o total de veículos é 40 e a
diferença entre o número de carros e motos é 6. Qual é o número de carros e
motos?
R: 23 carros e 17 motos
x
R: a largura é igual a 16 cm e o comprimento igual a 21cm.
x+5
l) A metade de um número adicionado ao número 1 tem, como
resultado, o dobro desse número. Qual é esse número? Resp: 2/3
2
20/07/2015
j) Um avô repartiu entre seus três netos a quantia de R$ 465,00. O neto mais
velho recebeu R $ 30,00 a mais que o neto mais novo, e o neto do meio
recebeu R$ 15,00 a mais que o neto mais novo. Quanto cada neto recebeu?
R: o mais velho 170 reais, o do meio 155 reais e o mais novo 140 reais.
k) O perímetro de um retângulo mede 74 cm. Quais são suas medidas, sabendose que o comprimento tem cinco centímetros a mais que a largura?
2.x + 2.(x +5) = 74
x
x+5
2x + 2x + 10 = 74
x= 16
4x = 64
R: a largura é igual a 16 cm e o comprimento igual a 21cm.
4x = 74 - 10
m) Três números naturais e consecutivos tem soma igual a 33.
Resp: Os números são 10, 11 e 12.
Quais são esses números?
n) Uma quantia em dinheiro foi dividida para três amigos:
Ian, Yuri e Luan. Sabe-se que Ian ganhou um terço do que
Yuri e Luan ganhou o dobro de Yuri. Sabendo que os três
amigos juntos tem R$ 420,00, quanto cada um recebeu?
Resp: Yuri: R$126,00 / Ian: R$ 42,00 / Luan: R$ 252,00
o) A soma de um número natural com o dobro de seu
sucessor resulta 104. Qual é esse número? Resp: O número é 34.
p) A idade de Antonia é o quíntuplo da idade de Sônia.
Considerando que, juntas, têm 78 anos, qual a idade de cada
uma? Resp: Sônia tem 13 anos e Antonia tem 65 anos.
q) Somando as idades de Bruno e Bianca, obtemos 15 anos. Qual
é a idade de cada um, considerando que o dobro da idade de
Bruno é igual ao triplo da idade de Bianca?
Resp:A idade de Bruno é 9 anos e a idade de Bianca é 6 anos.
r) Qual a medida do comprimento do retângulo abaixo, sabendo
2
que sua área é igual a 200 cm ?
4
2x + 3
Resp: Então, o comprimento
mede:
2. (23,5) + 3=
47 + 3= 50 cm
3