25 - CIRCUITOS DE
CORRENTE CONTÍNUA
1. RESISTORES EM SÉRIE E EM
PARALELO:
PARALELO
• Resistores em série: V = I.R1 + I.R2 =
I.(R1 + R2) = I.Req , com Req = ∑Ri
1
Solução:
Primeiro se calcula a resistência
q
da associação
ç em
equivalente
paralelo:
Req = 1/[(1/R
[( 2 + 1/R3)] = 1/[(1/12
[(
+
1/6)] = 4Ω
Calcula-se, a seguir, a associação em série
d R
de
Req e R1
:
RTeq = R1 + Req = 2 + 4 = 6Ω
Calcula-se
C
l l
a corrente I1, para a
seguir determinar as tensões V1 e
Veq:
I = ε/RTeq = 6/6 = 1A Logo,
V1 = R1.I = 2.1 = 2V e
Veq
q = Req.
q I = 4.1 = 4V
2
Com a tensão Veq (mesma diferença de potencial que é aplicada
sobre R2 e R3), determina-se as correntes I2 e I3:
I2 = Veq/R2 = 4/12 = 0,33A e
I3 = Veq/R3 = 4/6 = 0,66A
------------------------------------------------------------------------------Regra geral: Calcule primeiro as associações de resistores mais
internas para as mais externas.
externas
Neste outro exemplo, calcule a:
• associação
ç de R1 e R2 em pparalelo ((Req1
q )
• associação de Req1 e R3 em série (Req2)
• associação de Req2 e R4 em paralelo
3
2. REGRAS DE KIRCHHOFF
•
Nem sempre é possível ter circuitos
que tenham somente malhas de
resistores, neles podem estar
inclusos fontes e outros elementos(o
que impede de se calcular as
q
)
resistências equivalentes).
• As duas regras de Kirchhoff(Regra
das Malhas e Regra dos Nós) que
são leis de conservação, auxiliam na
determinação de correntes e
dif
diferenças
d
de potenciais
i i nos
circuitos elétricos.
• Regra das Malhas (Conservação da
energia):
“A soma algébrica
é i dos aumentos e
diminuições (quedas)de potenciais
ao longo de qualquer ma-lha
fechada de qualquer circuito deve
ser zero
zero.”
4
Na prática, ao percorrermos
uma malha
malha, elevamos o
potencial quando tivermos
uma fonte (bateria) e
diminuimos o potencial
quando tivermos uma
carga (resistor) de tal
forma a manter o poten
potencial entre dois pontos desta malha constante
constante, num
estado permanente.
5
• Regra dos Nós (Conservação da
carga):
“Em qualquer ponto (nó) de um
circuito,, onde há divisão de
corrente, a soma das correntes
que chegam a um nó é igual à
soma das correntes que saem
deste nó.”
Isto quer dizer que a carga que
chega a um determinado nó por
uma de suas ramificações
ramificações, sai por
outras ramificações deste nó.
6
EXEMPLO: Calcular a
corrente em cada parte do
circuito da figura.
Solução: O 1º passo é identificar todos os
nós ((nos terminais através dos
componentes) a, b, c, d, e, f.
O2
2º passo é identificar todas as malhas
do circuito, que são 3. Malhas abcd,
aefd, befc.
Temos 3 incógnitas e precisamos de 3
equações para determiná-las:
O 3º passo é aplicar a regra dos nós ao
nó ‘b‘(equação 1):
I = I1 + I2 (i)
7
O 4º passo é aplicar a regra das malhas à duas das três malhas (2
equações):
q ç )
Malha ‘abcd’: 18V - (12Ω).I - (6Ω).I1 = 0 (ii)
Malha ‘befc’: 12V – (1Ω).I2 + (6Ω).I1 – (1Ω).I2 = 0 (iii)
Das equações (i) e (ii), temos:
3 – 2.(I1 + I2) – I1 = 3 – 3.I1 – 2.I2 = 0 (iv)
Das equações (iv) e (iii), temos:
12 – (3 – 3.I1) + 6.I1 = 0
Logo: I1 = -1A
1A *sinal negativo significa sentido inverso da
orientação da corrente que foi adotada
Substituindo em ((iv),
) temos: I2 = 3A
Logo, I = 2A
8
EXEMPLO: Qual deve ser o valor da
resistência R para se ter a maior
potência dissipada por efeito Joule
nesta resistência.
Solução:
Aplicando a regra das malhas de
Kirchhoff:
ε = r.I + R.I ou I = ε/(r
( + R))
Por outro lado a potência dissipada por
efeito Joule em R:
P = R.I
R I² = R.
R {ε
{ε²/[(r
/[(r + R)
R).(r
(r + R)]}
A potência será máxima quando dP/dR =
0, logo:
dP/dR = I² – R.2.I².[1/(r
R 2 I² [1/(r + R)] = 0 =>
R=r
O processo se chama casamento de
impedância
9
3 CIRCUITOS RC
3.
•
É um circuito contendo capacitores
e resistores (e, possivelmente,
baterias).
CIRCUITO RC SEM
BATERIA:
•
•
Assume-se que no instante t0 = 0, a
chave S esteja sendo fechada e que,
no circuito sem bateria, a carga
inicial do capacitor seja Q0 e sua
capacitância C;
Aplicando-se a regra das malhas de
Kirchhoff no instante t > t0:
Kirchhoff,
VR = VC => I.R = R. dQ/dt = Q/C =>
dQ/Q = (-1/RC).dt =>
∫ dQ/Q = -(1/RC).
-(1/RC) ∫ dt
Integrando em ambos os lados:
Q(t) = Q0.exp(-t/tc) com tc = R.C
10
I = dQ/dt = I0. exp(-t/tc) com I0 = Q0/RC = V0/R
A constante de tempo tc corresponde o tempo necessário para:
• a carga Q no capacitor chegar a 37% do valor de Q0, ou,
• a corrente I chegar
g a 37% do seu valor inicial V0/R,, ou
• Tempo em que o capacitor estaria completamente
descarregado se a sua taxa de descarga fosse constante.
11
CIRCUITO RC COM
BATERIA:
• No instante t0 = 0, fecha-se a
chave S e começa a circular uma
corrente I0 = ε/R, que vai
decrescendo à medida que
aumenta a carga no capacitor,
que inicialmente é zero(Q0 = 0).
• Por Kirchhoff:
ε = VR + VC = R.I + Q/C =
R.dQ/dt
R
dQ/dt + Q/C
cuja solução é dada por:
Q(t)) = C.ε.[1
Q(
[ – exp(-t/t
p( c)] e
I = dQ/dt = ε/R. exp(-t/tc)
12
• Balanço de energia:
• O trabalho efetuado pela bateria no processo de carga Qf:
W = Qf.ε = (ε²). C
• A energia armazenada no capacitor (é metade do trabalho):
U = ½.Q.V = ½.Qf.ε = ½.(ε²).C
• A outra metade da energia transforma-se em efeito Joule:
a taxa de energia no resistor fica dWR/dt = R.I² = R.[ε/r.
exp(-t/tc)]²
l
logo,
WR = ∫ [(ε²)/R].exp(-2t/t
[( ²)/R]
( 2t/tc)dt = [(ε²).RC]/2R.∫
[( ²) RC]/2R ∫ exp(-x)
( )
dx = ½.(ε²).C
oonde:
de: x = 2t/RC
/ C e dt
d = (RC/2)dx
( C/ )d
13
EXEMPLO: Uma bateria de 6V, resistência interna
desprezível, é usada para carregar um capacitor de 2µF
desprezível
através de um resistor de 100Ω. Calcular:
a) A corrente inicial:
I0 = ε/R = 6V/100Ω = 0,06A
b) A carga final do capacitor: Qf = C.ε = 2µF.6V = 12µC
c) A constante de tempo: tc = R.C = 100Ω.2µF = 200µs
d) O tempo para o capacitor ter 90% de sua carga máxima:
Q = 0,9.Q
0 9 Qf = 0,9.C.ε
0 9 C ε = ε.C.[1
ε C [1 – exp(-t/tc)]
logo,
exp(-t/RC)
p(
) = 1 – 0,9
, = 0,1
, => -t/RC = ln(0,1)
( , ) => t = 460µs
µ
14
4. AMPERÍMETROS,
VOLTÍMETROS
Í
E OHMÍMETROS
Í
• Galvanômetro de
d’Arsonval:constituído por uma
bobina percorrida por uma
corrente, que fica sob ação de um
torque magnético devido ao campo
magnético que a envolve (ímã
permanente), e este torque
(proporcional a corrente) é
contrabalanceado por outro torque
(da mola) e indicado por um desvio
numa escala. Usualmente tem uma
resistência interna Rg = 20Ω e uma
corrente de fim de escala da ordem
de I = 0,5mA. É a base de
voltímetros e amperímetros.
15
• Âmperímetros: medem a corrente que passa num
determinado pponto do circuito.
•
•
•
Devem ter resistência desprezível (não alterar potencial);
São colocados em série no circuito (corrente passa por eles);
Devem ter uma resistência shunt muito menor q
que a resistência do
galvanômetro em paralelo com o galvanômetro.
• Voltímetros: medem a diferença de potencial entre
d i pontos de
dois
d um circuito.
i i
•
•
•
Devem ter resistência infinita (não alterar corrente);
São colocados em paralelo com o circuito;
Deve ter uma resistência shunt muito grande ligada em série com o
galvanômetro.
16
•
Formas de colocar o amperímetro e
voltímetro no circuito:
--------------------------------------------------------EXEMPLO: Usar um galvanômetro com uma resistência
a)
de 20Ω, no qual uma corrente de 5.(10^-4)A provoca o
desvio sobre toda a escala,
escala para projetar:
Um amperímetro que indique 5A na escala inteira:
17
Solução:
Deve-se colocar uma resistência shunt RS em paralelo de tal
forma que:
Ig + IS = 5A (soma das correntes) e Vg = VS => Ig.Rg = IS.RS
((resistências
es s ê c s em
e paralelo
p
e o => mesmo
es o po
potencial),
e c ), logo:
ogo:
RS = (Rg.Ig)/IS = (20.5.10^-4)/(5-5.10^-4) = 2.10^-3Ω
b)Um voltímetro que leia 10V na escala inteira:
Solução:
Queremos escolher uma resistência shunt RS em série (mesma
corrente) de tal forma que a tensão sobre RS + Rg seja de
10V:
Rg.IIg + RS.IIS = 10V
Logo, RS = (10 – Rg.Ig)/Ig = (10 – 20.5.10^-4)/(5.10^-4) =
19.980Ω ≈ 20KΩ
18
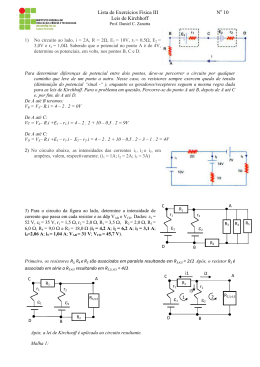
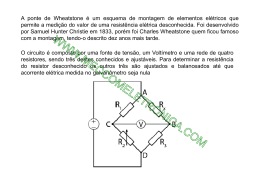
5. PONTE DE WHEATSTONE
• Método exato para medir resistências a partir de três
resistências conhecidas e um galvanômetro(vide figura);
• Consiste em modificar as resistências R1 e R2, de tal forma que
a corrente no galvanômetro seja zero;
• Por Kirchhoff, os potenciais sobre R1 e Rx, são iguais, assim
como os potenciais sobre R2 e R4, isto é:
I2.Rx = I1.R1 e I2.R4 = I1.R2
L
Logo:
Rx/R4 = R1/R2 ou Rx = R4.(R
(R1/R2)
19
• Na prática, usa-se, no lugar de R1
e R2, uma grande resistência
variável
iá l (condutor
( d t de
d
comprimento aproximado de
1m), de tal forma que a razão
entre
t os valores
l
das
d resistências
i tê i
são iguais à razão dos tamanhos
dos comprimentos dos fios
relativos
l i
a cada
d resistor;
i
• Na prática, usa-se uma
resistência em série com o
galvanômetro, para limitar a
corrente quando o circuito está
q
(próximo
(p
muito desequilibrado
do ponto de equilíbrio, esta
resistência é retirada para
aumentar a sensibilidade do
galvanômetro).
20
Lavnis e ednaldo amorim
21