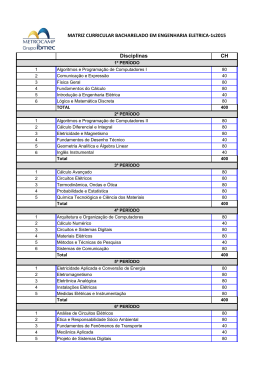
Universidade Federal do ABC
Engenharia de Instrumentação, Automação e Robótica
Circuitos Elétricos I
Prof. Dr. José Luis Azcue Puma

Potência em Regime Permanente Senoidal
1
Potência instantânea e potência média
𝜑 = 𝜃𝑉 − 𝜃𝐼
cos 𝐴 cos 𝐵 =
1
(cos 𝐴 + 𝐵 + cos(𝐴 − 𝐵))
2
2
Potência instantânea e potência média
Potência média
1
2
1
2
𝑃 = 𝑉𝑚 𝐼𝑚 cos 𝜃𝑉 − 𝜃𝐼 = 𝑉𝑚 𝐼𝑚 cos(𝜑) [ W ]
𝑃 = 𝑉𝐼 cos(𝜃𝑉 − 𝜃𝐼 ) = 𝑉𝐼 cos(𝜑) [ W ]
𝑉𝑚 , 𝐼𝑚  valores pico
𝑉, 𝐼  valores eficazes
3
Exemplo 1
Calcule a potência instantânea e a potência média absorvida
pelo circuito linear da figura abaixo. Considere que:
4
Exemplo 2
Calcule a potência média absorvida por cada um dos cinco
bipolos do circuito abaixo.
5
Valor efetivo ou eficaz
A potência dissipada pelo resistência
6
Valor efetivo ou eficaz
Da expressão de potência média
A potência média no resistor pode ser calculada também
através de:
7
Potência Aparente e Fator de Potência
Potência aparente
𝑷 = 𝑷𝒂𝒑 𝐜𝐨𝐬(𝜽𝑽 − 𝜽𝑰 )
𝑷 = 𝑷𝒂𝒑 𝐜𝐨𝐬(𝝋)
8
Exemplo 3
Calcule o fator de potência do circuito inteiro visto pela fonte
de tensão. Qual é o valor da potência média fornecida pela
fonte?
9
Potência Complexa
Considerando a carga Z da figura ao lado
e dados os fasores
𝑽 = 𝑽𝒎 ∠𝜽𝑽
𝑰 = 𝑰𝒎 ∠𝜽𝑰
A potência complexa absorvida é
𝟏 ∗
𝑺= 𝑽𝑰
𝟐
Ou
𝑺 = 𝑽𝒓𝒎𝒔 𝑰∗𝒓𝒎𝒔
𝑽𝒓𝒎𝒔 =
𝑽
𝟐
= 𝑽𝒓𝒎𝒔 ∠ 𝜽𝑽
𝑰𝒓𝒎𝒔 =
𝑰
𝟐
= 𝑰𝒓𝒎𝒔 ∠ 𝜽𝑰
10
Potência Complexa
𝑺 = 𝑽𝒓𝒎𝒔 𝑰∗𝒓𝒎𝒔
Logo
𝑺 = 𝑽𝒓𝒎𝒔 𝑰𝒓𝒎𝒔 ∠ (𝜽𝑽 − 𝜽𝑰 )
𝑺 = 𝑽𝒓𝒎𝒔 𝑰𝒓𝒎𝒔 𝒄𝒐𝒔 (𝜽𝑽 − 𝜽𝑰 ) + 𝒋𝑽𝒓𝒎𝒔 𝑰𝒓𝒎𝒔 𝒔𝒊𝒏 (𝜽𝑽 − 𝜽𝑰 )
P
Q
P  potência média (W)
Q  potência reativa (VAR)
11
Triângulo de potência
.
12
Conservação de potência
Todas as tensões e correntes estão expressados em valores
eficazes
(SERIE ou PARALELO)
13
Conservação de potência
As potências complexa, real e reativa das fontes é igual a soma
das potências complexa, real e reativa de cada uma das cargas
individuais.
14
Correção de Fator de Potência
O processo de aumentar o FP sem alterar a tensão ou corrente
da carga original é conhecido como correção de fator de
potência.
15
Correção de Fator de Potência
.
𝑄1  potência reativa original
𝑄2  potência reativa final
(após correção)
16
Transferência de potência em RPS
.
^I
fixa
2
Zi
E^i
P =
carga
R
( R + Ri ) 2 + ( X + Xi ) 2
Pmáx =
Ei  2
4R
para
Z = R + jX
Z
( ef )
gerador
Zi = Ri + j Xi
Potência ativa :
^ 2
P = R I 
Ei  2 Condição de máximo:
Z = Zi*
R = Ri
X = – Xi
 = 50 %
17
Transferência de potência em RPS
Quando a carga é puramente resistiva, o valor dessa carga
para máxima transferência de potência
𝑹𝑳 =
𝑹𝟐𝒕𝒉 + 𝑿𝟐𝒕𝒉 = 𝒁𝒕𝒉
18
Próxima Aula
1. Exercícios
19
Referências
[1] ORSINI, L.Q.; CONSONNI, D. “Curso de Circuitos Elétricos”, Vol.
1( 2ª Ed. – 2002 ), Ed. Blücher, São Paulo.
[2] CONSONNI, D. “Transparências de Circuitos Elétricos I”, EPUSP.
[3] BALDINI, R. “Transparências de Circuitos Elétricos”, UNICAMP.
[4] BELATI, E. “Transparências de Circuitos Elétricos I”, UFABC.
[5] NILSSON, J.W., RIEDEL, S. A. “Circuitos Elétricos”, 8ª Ed.,
Editora Pearson, 2009.
[6] C.K. Alexander; M.N.O.Sadiku, “Fundamentals of Electric
Circuits”, thrid edition.
[7] D.E. Johnson, J.L. Hilburn, J.R. Johnson “Fundamentos de Análise
de Circuitos Elétricos”, 4ta edição, Prentice Hall Brasil, 1994.
20