PROF. LUIZ CARLOS MOREIRA SANTOS
Questão 01)
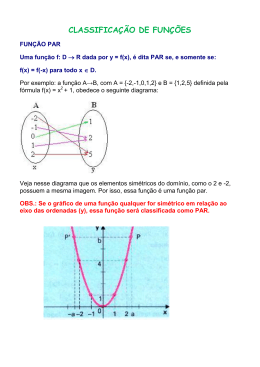
O conjunto A = {1, 2, 3, 4, 5} foi representado duas vezes, na forma de diagrama,
na figura abaixo.
Para definir uma função sobrejetora f : A → A, uma pessoa ligou cada elemento do
diagrama A1 com um único elemento do diagrama A2, de modo que cada elemento
do diagrama A2 também ficou ligado a um único elemento do diagrama A1. Sobre a
função f assim definida, sabe-se que:
•
•
f (f (3)) = 2
f (2) + f (5) = 9
Com esses dados, pode-se concluir que f(3) vale
a)
b)
c)
d)
e)
1.
2.
3.
4.
5.
Questão 02)
[
)
A função definida por f(x) = -3x2 – x + 4, de domínio − 16 , ∞ e contradomínio R, em
que R representa o conjunto dos números reais, é tal que
a) f é bijetora
b) f é injetora e não sobrejetora
c) f é sobrejetora e não injetora
d) f não é injetora, nem sobrejetora
Questão 03)
Dadas as funções f: ℜ → ℜ e g: ℜ → ℜ definidas por f(x) = x2 + 3 e g (x) = - 2x,
qual alternativa tem afirmação CORRETA?
a) f é uma função par e g é ímpar.
b) f e g são funções pares.
c) f e g são ímpares.
1
PROF. LUIZ CARLOS MOREIRA SANTOS
d) f é uma função ímpar e g é par.
e) f e g não são funções pares nem ímpares.
Questão 04)
Seja f:R → R; f(x) = x3
y
x
Então podemos afirmar que
a) f é uma função par e crescente.
b) f é uma função par e bijetora.
c) f é uma função ímpar e decrescente.
d) f é uma função ímpar e bijetora.
e) f é uma função par e decrescente.
Questão 05)
1
x
A equação x + = 0 admite:
a)
b)
c)
d)
e)
duas raízes reais, sendo uma a oposta da outra.
duas raízes reais, sendo uma a inversa da outra.
duas raízes racionais.
duas raízes não reais.
uma raiz real e outra não real.
Questão 06)
Seja D = R \ {1} e f : D → D uma função dada por
x +1
f (x) =
.
x −1
Considere as afirmações:
I. f é injetiva e sobrejetiva.
II. f é injetiva, mas não sobrejetiva.
III.
1
f (x) + f   = 0 ,
x
para todo x ∈ D, x ≠ 0.
IV. f(x) ⋅ f(–x) = 1, para todo x ∈ D.
Então, são verdadeiras:
a) apenas I e III.
b) apenas I e IV.
2
PROF. LUIZ CARLOS MOREIRA SANTOS
c) apenas II e III.
d) apenas I, III e IV.
e) apenas II, III e IV.
Questão 07)
Na tabela abaixo, X representa dias, contados a partir de uma data fixa, e Y representa medições feitas em
laboratório, nesses dias, para estudo de um fenômeno.
X 1 5 20 100 ...
Y 5 25 100 500 ...
De acordo com a tabela, pode-se afirmar que as grandezas são
a) diretamente proporcionais e relacionadas por uma função quadrática.
b) inversamente proporcionais e relacionadas por uma função linear.
c) diretamente proporcionais e relacionadas por uma função linear.
d) inversamente proporcionais e relacionadas por uma função quadrática.
Questão 08)
Todas as afirmações abaixo são corretas, EXCETO
a) Toda função crescente é injetora.
b) Toda função decrescente é injetora.
c) Toda função injetora é crescente.
d) Existem funções injetoras que são decrescentes.
Questão 09)
As tabelas a seguir representam algumas conjugações do verbo estar.
Tabela 1
Tabela 2
A
B
A
eu
estou
tu
estás
ele
está
nós
Tabela 3
B
A
eu
estava
tu
estavas
ele
estava
estamos nós
Tabela 4
B
A
eu
estivesse
eu
estaria
tu
estivesses
tu
estarias
ele
estivesse
ele
estaria
estávamos nós
estivéssemos nós
B
estaríamos
vós
estais
vós
estáveis
vós
estivésseis
vós
estaríeis
eles
estão
eles
estavam
eles
estivessem
eles
estariam
Das tabelas acima, a única que representa uma bijeção de A em B é a
a) Tabela 1.
b) Tabela 2.
c) Tabela 3.
d) Tabela 4.
Questão 10)
Cada um dos gráficos abaixo representa uma função y = f(x) tal que
f : D f → [−3, 4]; D f ⊂ [−3, 4] .
Qual deles representa uma função bijetora no seu domínio?
3
PROF. LUIZ CARLOS MOREIRA SANTOS
a)
b)
c)
d)
Questão 11)
“Estamos acostumados a considerar o tempo como uma linha reta, feita de sucessão
de instantes, ou como uma sucessão de “agoras” – um “agora” que já foi é o
passado, o “agora” que está sendo é o presente, um “agora” que virá é o futuro”.
ZACCUR, Edwiges. Metodologias abertas a iterâncias,
interações e errâncias cotidianas. In: GARCIA, R.L.
(org.). Método: pesquisa com cotidiano. RJ: DP&A, 2003.
O grifo no texto mostra como habitualmente costumamos considerar a passagem do
tempo. Dentre as funções abaixo, a que melhor representa essa consideração é:
a)
f (x) =
x 2 − 6x + 8
(2 x − 8)
4
PROF. LUIZ CARLOS MOREIRA SANTOS
b)
f (x ) = x 2 + y 2 − 2x
c)
f (x) =
d)
e)
f (x ) = x 2 + y 2 − 6x − 8y
x 2 + y 2 − 2y
x−2
f (x ) = x 2 + y 2 − 6x − 8y + 8
Questão 12)
Dadas as funções f (x ) =
1+ ex
1− ex
, x ∈ R – {0} g(x) = x sen x, x ∈ R, podemos afirmar
que:
a) ambas são pares
b) f é par e g é ímpar.
c) f é ímpar e g é par.
d) f não par e nem ímpar e g é par
e) ambas são ímpares.
Questão 13)
Considere a função f de R* em R definida por f ( x ) = x +
I. f é função ímpar
1
II. f   = f ( x )
x

III. f ( x ) + f (1) =  x +

1 


x
2
, se x > 0
Nessas condições,
a) somente I é verdadeira.
b) somente II é verdadeira.
c) somente III é verdadeira.
d) somente I e II são verdadeiras.
e) I, II e III são verdadeiras.
GABARITO:
1) Gab: A
2) Gab: B
3) Gab: A
5
1
x
e as afirmações:
PROF. LUIZ CARLOS MOREIRA SANTOS
4) Gab: D
5) Gab: D
6) Gab: A
7) Gab: C
8) Gab: C
9) Gab: A
10) Gab: D
11) Gab: A
12) Gab: C
13) Gab: E
6