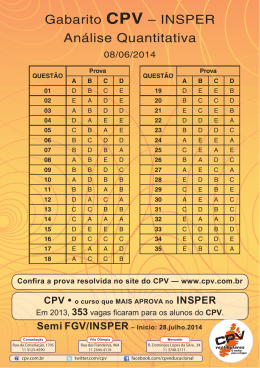
CPV seu Pé Direito no INSPER
INSPER Resolvida – 16/junho/2013 – Prova A (Marrom)
ANÁLISE QUANTITATIVA E LÓGICA
Utilize as informções a seguir para as questões 02 e 03.
01. Na figura está representado o preço de um console de
video game, em função do tempo decorrido desde o seu
lançamento.
A parte externa do palco de um teatro será construída tendo
como contorno um trecho de parábola.
Para projetá-la, um arquiteto usou um plano cartesiano e
desenhou a parábola de equação y = 1− x2, restrita aos quadrantes
correspondentes a y ≥ 0, conforme a figura a seguir.
Cada unidade nos eixos corresponde a 10 metros.
O preço do aparelho será menor do que 50% do valor de
lançamento a partir do:
a)6o mês
b)8o mês
c) 10o mês
d) 12o mês
e) 14o mês
Resolução:
Pelo gráfico, para y = 1,5 obtemos t = 14, ou seja,
a partir do 14o mês.
CPV
INSPERJUN2013
02. O chão do palco precisa ser recoberto com um revestimento
acústico especial, que é muito caro. Como o arquiteto não
dispõe de uma fórmula para calcular a área delimitada por
uma reta e uma parábola, ele decidiu estimá-la, obtendo um
valor mínimo e um valor máximo, usando:
Alternativa E
•
um triângulo de vértices sobre os pontos (0;1), (1; 0) e
(−1; 0).
• um trapázio de vértices sobre os pontos (1; 0), (−1; 0),
(−0,5; 1) e (0,5; 1).
Considerando as dimensões reais do palco, a diferença entre
os valores que ele obteve corresponde a:
a)
b)
c)
d)
e)
0,5 m2
1,0 m2
5,0 m2
10,0 m2
50,0 m2
1
2
INSPER – 16/06/2013
Seu Pé D ireito
nas
Resolução:
D
A
E
C
B
0
Como cada unidade do gráfico corresponde a 10 m, temos:
Área do ΔABC: Área do trapézio BCDE:
Portanto, a diferença é: 20 . 10
= 100 m2
2
(10 + 20) . 10
S2 =
= 150 m2
2
S1 =
S2 – S1 = 50 m2
03. Dada a dificuldade de se construir uma superfície que tem
um trecho de parábola como contorno, o arquiteto decidiu
trocar a forma do palco por um semicírculo de raio 1 (quando
representado no mesmo plano cartesiano). Entretanto, dois
trilhos de iluminação já estavam sendo construídos no
teto nas direções das retas y = x e y = − x, ligando o ponto
representado por (0; 0) aos respectivos pontos de encontro
das retas com a parábola.
Com essa alteração no projeto, o total de trilho adicional
necessário para os dois lados será igual a, aproximadamente,
Melhores Faculdades
a)
b)
c)
d)
e)
2,2 metros
3,2 metros
4,2 metros
5,2 metros
6,2 metros
2 ≈ 1, 4 e
(Use
Resolução:
y=–x
y=x
Alternativa E
G
F
H
I
A
INSPERJUN2013
B
0
Para obtermos o segmento IF = HG, devemos obter o ponto I
resolvendo o sistema:
y = x
CPV
2 ≈ 2, 2)
x =
Þ x2 + x – 1 = 0
x’ =
–1+
2
5
≈
– 1 + 2,2
2
–1–
2
5
≈
– 1 – 2,2
= –1,6
2
(não convém)
≈ 0,6
y = 1 – x2
O ponto I tem coordenadas I (0,6; 0,6).
Como OI é diagonal de um quadrado de lado 0,6, então:
OF = 0,6
Como OF é o raio da circunferência do raio 1, então OF = 10 m.
Logo, IF = HG = 10 – 8,4 = 1,6
Portanto, a medida do trilho adicional é: 2 . 1,6 = 3,2 m
2 ≈ 0,6 . 1,4 Þ OF ≈ 0,84 isto é, 8,4 m
Alternativa B
Seu Pé D ireito
nas
Melhores Faculdades
04. Considere que a seguinte declaração é verdadeira.
“Se todos os homens de bem preferem qualquer outra atividade à
política, então são governados por pessoas de outra natureza, nunca
por homens de bem.”
Se um homem de bem governa, pode-se deduzir que
necessariamente
a) todos os homens de bem preferem a política às outras
atividades.
b) pelo menos um homem de bem prefere a política a
alguma outra atividade.
c) todas as pessoas de outra natureza preferem a política
às outras atividades.
d) pelo menos uma pessoa de outra natureza prefere a
política às outras atividades.
e) nenhuma pessoa de outra natureza prefere a política às
outras atividades.
Resolução:
Um condicional do tipo “Se A, então B” é verdadeiro somente em
3 situações: V → V, F → V, F → F.
Temos então a declaração:
[se] NENHUM homem de bem prefere a política, [então]
NENHUM homem de bem governa.
Como o enunciado afirma que “um homem de bem governa”,
a segunda parte da proposição (o consequente) é seguramente
FALSA. Desse modo, é necessário que a primeira parte da
proposição (o antecedente) seja FALSA (afinal, se for verdadeira,
teremos V → F).
Logo, é falso que “nenhum homem de bem prefere a política”; ou
seja, é verdadeiro que “pelo menos um homem de bem prefere
a política”.
Alternativa B
INSPER – 16/06/2013
3
05. Jane retirou R$240,00 num caixa eletrônico que dispunha
de notas de R$50,00 e R$20,00, tendo recebido c cédulas
de R$50,00 e v cédulas de R$20,00.
A diferença entre c e v, em módulo, pode ser:
a)
b)
c)
d)
e)
no mínimo 2 e no máximo 5.
no mínimo 2 e no máximo 7.
no mínimo 2 e no máximo 12.
no mínimo 3 e no máximo 7.
no mínimo 3 e no máximo 12.
Resolução:
Temos as seguintes distribuições possíveis:
c
v
4
2
2
7
0
12
Então, a diferença em módulo entre c e v, pode ser no mínimo 2
e no máximo 12.
Alternativa C
INSPERJUN2013
CPV
4
INSPER – 16/06/2013
Seu Pé D ireito
nas
Utilize as informações a seguir para as questões 06, 07 e 08.
Um géografo deseja determinar a localização do pico de uma
montanha. Na região, há duas estradas retas, ambas no nível
do mar, sem subidas ou descidas ao longo de seus percursos,
que se cruzam formando um ângulo reto. Ele conta com um
instrumento que lhe permite observar o pico por meio de uma
luneta e registrar:
•
•
o ângulo de observação, formado pela reta que liga o ponto
em que está o aparelho e o pico com o plano formado pelas
duas estradas;
a distância aproximada entre o ponto de observação e o pico.
Melhores Faculdades
Está mais distante do pico o ponto
a)A
b)B
c) C
d) D
e) E
Resolução:
Projetando os pontos A, B, C, D e E sobre a mesma reta em relação
ao pico da montanha, temos:
pico
Os eixos da figura a seguir representam as duas estradas e os
pontos A, B, C, D e E correspondem a locais onde ele fez as
suas primeiras observações.
45º
40º
E
Cada unidade nos eixos corresponde a 1 quilômetro.
06. Os ângulos de inclinação entre o plano determinado pelas
estradas e as retas ligando os pontos de observação com o
pico foram registrados na tabela.
CPV
INSPERJUN2013
37º
D
34º
B
Portanto, o ponto mais distante é o C.
31º
A
C
Alternativa C
Seu Pé D ireito
nas
Melhores Faculdades
07. Como estava com dificuldades para determinar a altura do
pico em relação ao nível do mar, o géografo fez diversas
outras medições em pontos da estrada representada pelo
eixo x. Nesse processo, ele encontrou um ponto F em que
o ângulo entre o plano das estradas e a reta que o ligava
ao pico era exatamente 30o. Seu aparelho mostrou que a
distância entre o ponto F e o pico era igual a 6 km.
A altura do pico em relação ao nível do mar é igual a
a)
b)
c)
d)
e)
6 km
5 km
4 km
3 km
2 km
5
08. Para determinar a projeção do pico da montanha no plano
representado na figura, o géografo pensou em fazer diversas
observações ao longo das duas estradas. Ele o faria até que
encontrasse pontos equidistantes da projeção do pico.
Para que seja determinada esta localização,
Resolução:
INSPER – 16/06/2013
A figura relacionada à questão é:
a) é suficiente encontrar dois pontos equidistantes distintos
na mesma estrada.
b) é suficiente encontrar dois pontos equidistantes distintos,
sendo um em cada estrada.
c) é necessário encontrar três pontos equidistantes distintos
dois a dois na mesma estrada.
d) é suficiente encontrar três pontos equidistantes distintos
dois a dois.
e) é necessário encontrar quatro pontos equidistantes
distintos dois a dois.
Resolução:
y
6
km
h
30º
Então, sen 30º =
h
Þ h = 3 km
6
D
Alternativa D
P
C
A
B
x
A projeção ortagonal do pico sobre o plano é o centro da
circunferência cujo raio é a medida feita pelo geógrafo. Se este
tomasse apenas 2 pontos dentre A, B, C e D, o pico estaria em um
ponto qualquer da mediatriz do segmento de reta determinado por
estes pontos.
Portanto, seria necessário um terceiro ponto para encontrarmos
as coordenadas do ponto pedido.
Obs: Se considerarmos que o geógrafo considera a medida da distância do ponto
de observação até a projeção, bastariam apenas 2 pontos na mesma reta, o que nos
conduziria à alternativa A.
Alternativa D
INSPERJUN2013
CPV
6
Seu Pé D ireito
INSPER – 16/06/2013
nas
09. Uma doceira vende bombons artesanais em embalagens
individuais (por R$5,00 a unidade), caixas com 12 (por R$51,00
cada uma) ou pacotes com 24 (por R$96,00 cada um).
Há também uma promoção: comprando x embalagens
individuais, o cliente ganha x% de desconto, para x ≤ 50.
Comparando os preços, é correto concluir que comprar
bombons pela promoção é
a) mais vantajoso para um cliente que quiser 12 ou 24
unidades do que adquiri-las na caixa ou no pacote,
respectivamente.
b) mais vantajoso para um cliente que quiser 24 unidades
em relação ao preço do pacote, mas não para quem
quiser 12.
c) mais vantajoso para um cliente que quiser 12 unidades em
relação ao preço da caixa, mas não para quem quiser 24.
d) menos vantajoso tanto para um cliente que quiser 12
unidades quanto para quem quiser 24, em relação aos
preços da caixa ou do pacote, respectivamente.
e) indiferente tanto para um cliente que quiser 12 unidades
quanto para quem quiser 24.
Resolução:
(
)
x
O preço da promoção é 5x 1 –
; os preços para 12 e 24
100
unidades são respectivamente, 52,8 e 91,20.
Portanto, é mais vantajoso para um cliente que quer 24
unidades mas não para aquele que quer 12 unidades.
Alternativa b
CPV
INSPERJUN2013
Melhores Faculdades
Seu Pé D ireito
nas
Melhores Faculdades
INSPER – 16/06/2013
7
10. Gilson está fazendo dez treinos para uma corrida de 15 quilômetros. A cada treino ele faz o pecurso da corrida e registra seu
tempo. A recomendação de seu treinador é que consiga um tempo médio de 1h30min, considerando os dez treinos. Os tempos
dos treinos já realizados constam na tabela a seguir.
Para que Gilson consiga atingir o tempo médio recomendado pelo seu treinador, nos três últimos treinos ele deve manter um
tempo médio de no máximo
a)
b)
c)
d)
e)
1h25min
1h26min
1h27min
1h28min
1h29min
Resolução:
Calculando a média para as 10 tomadas de tempo com todo os valores em minutos
102 + 80 + 96 + 93 + 84 + 94 + 96 + T8 + T9 + T10
10
= 90
T8 + T9 + T10 = 255 min.
A média dos 3 últimos tempos é =
255
= 85 = 1h 25 min
3
Alternativa A
INSPERJUN2013
CPV
8
INSPER – 16/06/2013
Seu Pé D ireito
nas
Utilize as informações a seguir para as questões 11 e 12.
Melhores Faculdades
c)
d)
Em um torneio de apostas, cada participante recebe 50 fichas.
Ao longo do torneio, eles podem apostar qualquer quantidade de
fichas com qualquer outro participante. Em toda aposta, um ganha
e outro perde as fichas apostadas. 100 pessoas entraram nesse
torneio e, ao final, foram identificados os 30 que tinham acabado
com mais fichas (Grupo G) e os 30 que tinham acabado com
menos fichas (Grupo P). A organização registrou o total de fichas
de todos os participantes em 4 momentos do torneio.
A tabela abaixo mostra as somas das fichas das pessoas dos
Grupos G e P nas 4 contagens feitas.
11. O gráfico que melhor expressa a soma das fichas daqueles
que não estão no Grupo G e nem no Grupo P é:
a)
e)
b)
Resolução:
Somando o total de fichas em cada uma das quatro contagens e
subtraindo esse resultado de 5000, teremos o total de fichas que
não pertencem ao grupo G e ao grupo P.
Contagem
Soma de P e G
CPV
INSPERJUN2013
1
2
3
4
5000
5000
5000
5000
3600
4200
3400
4200
1400
800
1600
800
Assim, o gráfico correto é o da Alternativa A
Seu Pé D ireito
nas
Melhores Faculdades
12. Ao final do torneio, não havia dois participantes que tivessem
o mesmo número de fichas. Júlio, um dos participantes,
terminou com o maior número de fichas entre todos os 100.
Júlio chegou ao fim do torneio com, no máximo,
a)
b)
c)
d)
e)
149 fichas.
150 fichas.
499 fichas.
500 fichas.
4900 fichas.
INSPER – 16/06/2013
9
13. Na figura, P1 é o ponto médio de AC, P2 é o ponto médio de
P1C, P3 é o ponto médio de P2C, e assim sucessivamente, em
uma sequência infinita de pontos. Além disso, o lado de cada
triângulo que está contido no eixo x mede a metade do lado
do triângulo anterior.
Resolução:
Para a resolução desta questão é importante salíentar que não
iremos considerar que o jogo acabou na quarta rodada.
Assumindo que Júlio terminou com o maior número de fichas
e todos os perdedores estão com números diferentes de fichas
podemos distribuilos em P.A da seguinte forma:
Então Júlio acabou o jogo com no máximo 149 fichas.
Alternativa a
0, 1, 2, 3, 4, ..., 98 assim
(0 + 98) 99
2
= 4851
A soma das áreas dos triângulos sombreados é igual a:
a)8
b) 7
c) 6
d) 5
e) 4
Resolução:
Pela figura:
S1 =
1
5 15
.3. =
2
2 4
1 3 5 15
S2 = . . =
2 2 4 16
1 3 5 15
S3 = . . =
2 4 8 64
Assim, a soma das infinitas áreas dos triângulos é igual a:
S=
15
4
1-
1
4
=5
Alternativa D
INSPERJUN2013
CPV
10
INSPER – 16/06/2013
Seu Pé D ireito
nas
14. Se 1, α e β são as raízes da função f (x) = x3 + 4x2 − 55x + 50,
então 1 + α2 + β2 é igual a:
a)
b)
c)
d)
e)
4
50
55
101
126
Melhores Faculdades
Utilize as informações a seguir para as questões 15 e 16.
O gráfico a seguir mostra as temperaturas registradas em uma
cidade localizada numa região serrana ao longo de um dia inteiro.
Resolução:
Se x = 1 é raiz de f (x) = x3 + 4x2 – 55x + 50, então:
1
1
4 –55 50
1
5 –50
0
f (x) = (x – 1) . (x2 + 5x – 50) = (x – 1) . (x – 5) . x + 10
Assim, as raízes de f (x) são 1, 5 e –10.
Logo, 1 + α2 + β2 = 126
Alternativa E
15. Os horários do dia em que a temperatura estava mais alta e
mais baixa foram, respectivamente,
a)
b)
c)
d)
e)
0h e 24h.
17h e 7h.
0h e 17h.
7h e 24h.
17h e 24h.
Resolução:
CPV
INSPERJUN2013
Observando o gráfico, temos que a temperatura mais alta ocorreu
às 0 h (25ºC), e a mais baixa às 24 h (8,5ºC)
Alternativa A
Seu Pé D ireito
nas
Melhores Faculdades
INSPER – 16/06/2013
16. O aquecedor de uma residência nessa cidade está programado
para funcionar sempre que a temperatura fica abaixo de
16oC. Durante esse dia, este aquecedor ficou ligado por,
aproximadamente,
17. O número de soluções reais da equação
é igual a:
a)
b)
c)
d)
e)
a)1
b) 2
c) 3
d) 4
e) 5
Resolução:
Observando o gráfico, temos que a temperatura fica abaixo de
16ºC, nos seguintes intervalos de horas:
das 4 h às 11 h Þ 7 horas
e
das 21 h às 24 h Þ 3 horas
Assim, o total de horas que o aquecedor fica ligado neste dia é de
10 horas.
Alternativa C
3h
7h
10h
14h
17h
11
x4 log7 x − 16 log7 x = 0
Resolução:
* temos:
Para x Î R ,
+
(x4 – 16) . log7 x = 0 Þ x = 2 ou x = 1.
Portanto, são 2 soluções reais.
Alternativa B
INSPERJUN2013
CPV
12
INSPER – 16/06/2013
Seu Pé D ireito
nas
Utilize as informações a seguir para as questões 18 e 20.
Um modelo probabilístico foi criado para ajudar a polícia
rodoviária a identificar motoristas potencialmente problemáticos.
O modelo aponta, de acordo com as características do veículo,
comportamento do motorista e velocidades registradas nos
radares, as probabilidades de o indíviduo:
Perfil A: causar um acidente grave;
Perfil B: cometer uma infração de trânsito;
Perfil C: dirigir de forma segura e responsável.
Para cada pessoa, o modelo calcula três valores a, b e c,
dos quais resultam as probabilidades dos três perfis, dadas,
respectivamente, por:
• pA =
• pB =
• pC =
2a
2a + 2b + 2c
2b
2a + 2b + 2c
2c
2a + 2b + 2c
A maior dessas 3 probabilidades indica o perfil do motorista
correspondente.
18. Quando a soma das probabilidades pA e pB, para um
determinado motorista, superar 35%, a polícia rodoviária
deve submetê-lo ao teste do bafômetro. A tabela abaixo
mostra os valores de a, b e c determinados pelo sistema
para 4 motoristas.
Resolução:
Considerando os valores da tabela dada temos para:
Motorista 1
pA =
21
= 2
20
21 + 21 + 24
= 1 e
10
pB =
= 1
10
21
= 2
20
21 + 21 + 24
pA + pB =
Motorista 2
pA =
= 1
4
pB =
pA + pB =
Motorista 3
pA =
= 1
5
pB =
pA + pB =
Devem ser submetidos ao teste do bafômetro apenas os
motoristas:
a)
b)
c)
d)
e)
CPV
1e2
1e3
2e3
2e4
3e4
INSPERJUN2013
Melhores Faculdades
1
5
< 35%
22
= 4
16
22 + 22 + 23
22
16
1
2
= 1
4
> 35%
24
= 16
80
24 + 25 + 25
25
80
3
5
= 2
5
> 35%
Portanto, devem ser submetidos ao teste do bafômetro apenas os
motoristas 2 e 3
Alternativa C
Seu Pé D ireito
nas
Melhores Faculdades
19. Durante o processamento, o computador que executa o
modelo somente consegue efetuar operações com números
inteiros menores ou iguais a 999.999.999.
Das possibilidades de combinações de valores a seguir, a
única que permitirá ao computador efetuar as operações é:
a)
b)
c)
d)
e)
a = 30, b = 10 e c = 22
a = 2, b = 31 e c = 15
a = 18, b = 7 e c = 32
a = 35, b = 3 e c = 2
a = 27, b = 10 e c = 22
Resolução:
Quando calculamos 210 obtemos 1024 que vale aproximadamente
103.
Então, 230 = (210)3 @ (103)3 = 109 = 1.000.000.000 > 999.999.999.
13
INSPER – 16/06/2013
20. Para simplificar os cálculos, um analista percebeu que, para
a grande maioria dos motoristas, ele poderia fixar c = 1 e
fazer a = b. Para esses casos, ele pode programar o sistema
para calcular pA pela fórmula:
1
a)
2 + 21 – a
b)
c)
d)
e)
A única alternativa que possui todos os expoentes menores do que
30 é a E. Portanto
Alternativa E
2a
1 + 21 – a
1
2a + 2 – a
2a
2a + 21 – a
2–a
1+2–a
Resolução:
pA =
=
2a
2a + 2a +
1
2 + 21–a
2
=
2a
2(2a
+ 1)
.
2–a
2–a
=
1
2(1 + 2–a)
=
Alternativa A
INSPERJUN2013
CPV