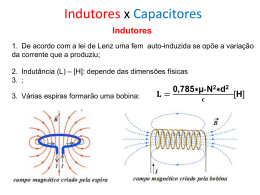
Introdução
Circuitos Elétricos
• Os circuitos que estudamos até o momento são considerados
condutivamente acoplados.
– Um laço afeta o laço vizinho através da condução de corrente.
Circuitos Magneticamente Acoplados
Alessandro L. Koerich
Engenharia de Computação
Pontifícia Universidade Católica do Paraná (PUCPR)
• Quando dois laços com ou sem contato se afetam através do
campo magnético gerado por um deles, são chamados de
magneticamente acoplados.
• Exemplo: Transformador → bobinas magneticamente
acopladas para transferir energia de um circuito para outro.
Indutância Mútua
Indutância Mútua
•
Quando dois indutores (ou bobinas) estão próximos, o fluxo
magnético causado pela corrente em uma bobina induz tensão na
outra bobina.
•
Mas o fluxo φ é produzido pela corrente i, portanto qualquer
mudança em φ é causada por uma variação na corrente:
=
•
Este fenômeno é chamado de indutância mútua.
•
Para um indutor simples de N
espiras, quando uma corrente i
flui através dele, um fluxo
magnético φ é produzido ao redor
dele.
•
De acordo com a lei de Faraday, a tensão induzida no indutor é:
•
•
=
ou
=
A indutância L do indutor é dada por:
=
Esta indutância é chamada de auto-indutância, pois relaciona a
tensão induzida em uma bobina por uma corrente variante no tempo
na mesma bobina.
Indutância Mútua
Indutância Mútua
• Considerando agora duas bobinas com auto-indutâncias L1 e
L2 que estão próximas. A bobina 1 tem N1 voltas e a bobina 2
tem N2 voltas. Assumimos que a bobina 2 não transporta
corrente.
• Apesar das duas bobinas estarem fisicamente separadas,
elas estão magneticamente acopladas. Como o fluxo total φ1
percorre a bobina 1, a tensão induzida na bobina 1:
=
• O fluxo magnético φ1 originário na bobina 1 tem dois
componentes: o componente φ11 percorre somente a bobina 1
e o componente φ12 percorre ambas as bobinas. Portanto:
=
• Somente o fluxo φ12 percorre a bobina 2, logo a tensão
induzida na bobina 2:
=
+
Indutância Mútua
•
Novamente, como os fluxos são causados pela corrente i1 fluindo na bobina 1:
=
•
onde
=
/
Indutância Mútua
•
Supondo agora que a corrente i2 flui na bobina 2, enquanto a bobina
1 não transporta corrente.
=
=
+
é a auto-indutância da bobina 1. Da mesma maneira:
=
=
onde:
=
•
•
Como o fluxo total φ2 percorre a bobina 2, a tensão induzida na
bobina 2:
M21 é a indutância mútua da bobina 2 com respeito a bobina 1. O índice 21
indica que a indutância relaciona a tensão induzida na bobina 2 à corrente na
bobina 1. Assim, a tensão mútua em circuito aberto (ou tensão induzida) sobre a
bobina 2 é:
=
=
•
onde
=
/
=
=
é a auto-indutância da bobina 2.
Indutância Mútua
• Da mesma maneira:
Indutância Mútua
• Veremos que:
=
=
=
=
=
• M é a indutância mútua entre duas bobinas. É medida em
henrys (H).
onde:
=
• M12 é a indutância mútua da bobina 1 com respeito a bobina 2.
O índice 12 indica que a indutância relaciona a tensão
induzida na bobina 1 à corrente na bobina 2. Assim, a tensão
mútua em circuito aberto (ou tensão induzida) sobre a bobina
1 é:
• Note que o acoplamento mútuo existe somente se as bobinas
estiverem próximas e os circuitos forem alimentados por
fontes variantes no tempo.
Indutância Mútua é a capacidade de um indutor induzir uma
tensão sobre um indutor vizinho, medida em henrys (H).
=
Indutância Mútua
Indutância Mútua
• Convenção do ponto para a análise de circuitos:
– A polaridade da indutância mútua depende dos aspectos construtivos.
– A convenção de pontos eliminada a necessidade de descrever os
aspectos construtivos em circuitos
• Um ponto é colocado no circuito em um dos terminais de cada
um dos indutores acoplados magneticamente.
• Indica a direção do fluxo magnético se a corrente entra pelo
terminal marcado com o ponto.
• A convenção dos pontos diz o seguinte:
Se uma corrente entra pelo terminal com o ponto de uma bobina,
a polaridade de referência da tensão mútua na segunda bobina
é positiva no terminal com o ponto da segunda bobina.
• ou
Se uma corrente sai pelo terminal com o ponto de uma bobina, a
polaridade de referencia da tensão mútua na segunda bobina é
negativa no terminal com o ponto da segunda bobina.
• Assim, a polaridade de referencia de um tensão mútua
depende da direção de referencia da corrente induzida e os
pontos nas bobinas acopladas.
Indutância Mútua
Indutância Mútua
• A aplicação da convenção de
pontos pode ser ilustrada pelas
figuras ao lado:
• A convenção de pontos, para indutores conectados em série,
pontos se somando, a indutância total será:
= + +2
• Para indutores conectados em série, com pontos opostos, a
indutância total será:
= + −2
Análise de Circuitos Envolvendo
Indutâncias Mútuas
•
Aplicando a LTK na malha1:
=
Análise de Circuitos Envolvendo
Indutâncias Mútuas
•
+
+
•
•
Aplicando a LTK na malha 2:
=
•
+
+
Aplicando a LTK na malha 1:
=
+
Aplicando a LTK na malha 2:
0=−
+
+
+
•
As equações acima podem ser resolvidas da maneira usual para
encontrar as correntes.
•
Note que assumiremos sempre que a indutância mútua e a posição
dos pontos são fornecidas.
Passando para o domínio da frequência:
=
=
+
+
+
+
Energia em Circuitos Acoplados
Energia em Circuitos Acoplados
•
•
A energia armazenada em um indutor:
1
=
2
A energia armazenada em dois indutores
acoplados magneticamente, assumindo
que a corrente entra nos terminais com
ponto em ambos indutores:
=
•
1
2
+
1
2
1
2
+
1
2
O limite superior para a indutância mútua M:
≤
•
Ou seja, a média geométrica das auto-indutâncias dos indutores.
•
O coeficiente de acoplamento, mostra o quanto a indutância mútua
se aproxima de seu limite superior:
+
=
Se uma corrente entra pelo terminal com o ponto em um indutor e
sai pelo terminal com ponto no outro indutor:
=
•
−
Energia em Circuitos Acoplados
• Se todo o fluxo produzido por um indutor atinge outro, então k
= 1 e temos uma acoplamento 100% ou perfeitamente
acoplados.
• Para k < 0,5 temos indutores fracamente acoplados.
•
onde 0 ≤ ≤ 1. O coeficiente de acoplamento é a fração do fluxo
total emanando de um indutor que conecta ao outro indutor:
=
=
+
=
=
+
Transformador Linear
• É um dispositivo magnético que utiliza o fenômeno da
indutância mutua.
• Um transformador é geralmente um dispositivo de quatro
terminais compreendendo dois ou mais bobinas acopladas
magneticamente.
• Para k > 0,5 temos indutores fortemente acoplados.
• O coeficiente de acoplamento é
uma medida do acoplamento
magnético entre dois indutores;
0 ≤ ≤ 1.
• A bobina conectada diretamente a uma fonte de tensão é
chamado de enrolamento primário.
• A bobina conectada a carga é chamada de enrolamento
secundário.
• As resistências representam as perdas nas bobinas.
Transformador Linear
Transformador Linear
• Um transformador é considerado linear se as bobinas são
enroladas em um material magnético linear (permeabilidade
magnética constante), como baquelite, ar, plástico e madeira.
• Para simplificar a análise é possível substituir o acoplamento
magnético por um circuito equivalente T (ou Y) ou Π (ou Δ)
que não contém a indutância mútua:
• Para obtermos a impedância de entrada, aplicamos a LTK
nas duas malhas, e temos:
• Circuito equivalente T:
=
=
+
+
=
+
+
,
=
−
,
=
+
– O primeiro termo ( +
) é a impedância primária.
– O segundo termo é devido ao acoplamento entre os enrolamentos
primário e secundário e é chamada de impedância refletida ao primário:
=
−
• Circuito equivalente Π:
=
−
−
,
=
−
−
,
=
−
+
Transformador Ideal
Transformador Ideal
• Um transformador ideal é aquele com acoplamento perfeito (k
= 1).
• Transformadores com núcleo de ferro são uma aproximação
de transformadores ideais.
• Consiste em duas bobinas com um número grande de voltas
em um núcleo comum de alta permeabilidade. Devido a esta
alta permeabilidade do núcleo, o fluxo liga todas as voltas de
ambas as bobinas, resultando portanto em um acoplamento
perfeito.
• De acordo com a Lei de Faraday,
as tensões sobre os enrolamentos
primário e secundário são
respectivamente:
• Um transformador é dito ser ideal se:
– As bobinas tiveram reatâncias bastante elevadas (L1, L2, M → ∞);
– O coeficiente de acoplamneto é unitário (k=1);
– Os enrolamentos primário e secundário não possuem perdas (R1 = R2=
0).
=
=
Transformador Ideal
• Dividindo as equações anteriores temos:
=
=
Transformador Ideal
• Pelo princípio da conservação da energia, temos:
=
• Na forma fasor, temos:
=
onde n é a razão de voltas ou razão de transformação.
• Mostrando que as correntes primária e secundária estão
relacionadas à razão de voltas de maneira inversa que as
tensões, então:
1
=
=
• Usando fasores, temos:
=
=
Transformador Ideal
=
=
=
1
• Quando n=1, chamamos o transformador de transformador de
isolamento.
• Se n>1 temos um transformador elevador, pois a tensão
aumenta do primário para o secundário (V2>V1).
• Se n<1 temos um transformador abaixador, pois a tensão
decresce do primário para o secundário (V2<V1).
Transformador Ideal
• Quanto a polaridade das tensões e direção das correntes,
temos:
1.
Se V1 e V2 são ambas positivas
ou ambas negativas nos
terminais com ponto, use +n.
Caso contrário use –n.
2.
Se tanto I1 quanto I2 entram
ou ambas saem dos terminais
com ponto, use –n.
Caso contrário use +n.
Transformador Ideal
• A potência complexa no enrolamento primário é:
∗
=
=
(
)∗ =
∗
=
• Não há perda de potência. O transformador ideal não absorve
potência.
• A impedância de entrada vista pela fonte:
1
=
=
• Mas como
⁄
=
Transformador Ideal
• Uma prática comum na análise de circuitos é eliminar o
transformador, refletindo as impedâncias e fontes de um lado
do transformador para o outro.
• Refletindo o lado secundário para o primário:
– Obtemos o equivalente de Thevenin do circuito a direita dos terminais ab.
– Obtemos VTh como a tensão de circuito aberto nos terminais a-b.
– Obtemos ZTh removendo a fonte tensão no enrolamento secundário e
inserindo uma fonte unitária nos terminais a-b.
– Tendo VTh e ZTh adicionamos o equivalente de Thevenin à esquerda de
a-b.
, então:
=
Transformador Ideal
• Refletindo o lado secundário para o primário:
Transformador Ideal
• A regra geral para eliminar o transformador e refletir o circuito
secundário para o lado do primário é: dividir a impedância
secundária por n2, dividir a tensão secundária por n e
multiplicar a corrente secundária por n.
• Para refletir o lado primário do circuito para o lado secundário:
– A regra para eliminar o transformador e refletir o circuito primário para o
lado secundário é: multiplicar a impedância primária por n2, multiplicar a
tensão primária por n e dividir a corrente primária por n.
=
=