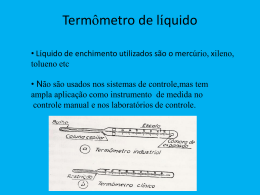
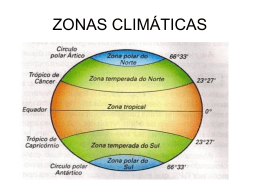
UNIVERSIDADE
CATÓLICA DE
BRASÍLIA
PRÓ-REITORIA DE GRADUAÇÃO
TRABALHO DE CONCLUSÃO DE CURSO
Curso de Física
PAR TERMOELÉTRICO
Autor: Alexandre Ângelo Batista
Orientador: Prof. Dr. Armando de Mendonça Maroja
BRASÍLIA
2007
Alexandre Ângelo Batista
Par termoelétrico
Trabalho de Conclusão de Curso
submetido à Universidade Católica
de Brasília para obtenção do Grau
de Licenciado em Física.
Orientador:
Dr.
Mendonça Maroja.
Águas Claras
Dezembro de 2007.
Armando
de
PAR TERMOELÉTRICO:
Resumo: neste trabalho, descrevem-se alguns aspectos da termometria e os novos métodos
de medição da temperatura, que foram desenvolvidos para alcançar maior precisão nas
medidas de baixas e altas temperaturas. A invenção dos termômetros e a maneira como são
construídos foram reconhecidos como um grande desenvolvimento para a ciência e para as
indústrias. Os sensores de temperatura como pares termoelétricos vêm tendo preferência nas
indústrias pela sua precisão, simplicidade de operação e em seus resultados positivos.
Existem propostas para substituir os termômetros de mercúrio por termômetros digitais com
intuito de preservar o meio ambiente. Por fim realizamos a aferição de pares termoelétricos de
Ferro – Cobre e Cobre – Constantan.
.
Palavra – chave: termometria, termômetros e par termoelétrico.
1.0 INTRODUÇÃO:
Definição de temperatura:
A grandeza física temperatura é definida como o grau de agitação das
moléculas que constituem um corpo. Logo, quanto mais rápido o movimento das
moléculas, mais “quente” apresenta-se o corpo.
Temperatura é uma propriedade associada a um determinado estado térmico
que nos permite dizer se dois ou mais corpos estão, ou não em equilíbrio térmico. Ela
é representada em uma escala numérica a qual demonstra que quanto maior o seu
valor, maior será a energia cinética média dos átomos do corpo em questão.
Por vezes, o conceito de temperatura é confundido com os conceitos de energia
térmica e de calor, então é importante saber que: energia térmica, a qual depende da
temperatura, da massa e do tipo de substância, é o somatório das energias cinéticas
dos seus átomos, e que calor é a energia em trânsito ou a forma de energia que é
transferida através da fronteira de um sistema em virtude da diferença de temperatura.
Na antigüidade, próximo ao fim do século XV, as primeiras noções de
temperatura foram apresentadas. Essas, surgiram a partir das sensações que se
notava através do tato, daí dizia-se que algo estava quente ou frio. Aquele era um
conhecimento empírico em relação ao calor e à temperatura.
O corpo humano induzir ao erro quanto à medição da temperatura, pois ao tocar
em materiais de diferentes composições químicas, os quais podem ser avaliados
como bons condutores ou maus condutores térmicos, tem-se a sensação de quente ou
frio dependendo do condutor . Pela necessidade de maior exatidão para medir a
temperatura de diferentes corpos no mesmo ambiente criou-se o termômetro.
3
A construção de um termômetro obedece a certas convenções. Nelas, os
números são associados aos diferentes estados térmicos e quando em equilíbrio, os
corpos são representados pelo mesmo número. Na construção dos termômetros são
utilizadas grandezas físicas que variam de forma linear com a temperatura. Como
exemplo dessas grandezas temos: volume de um líquido, comprimento de um sólido,
resistência elétrica de um fio, pressão ou volume de um gás.
Junto com a construção dos termômetros, também veio a necessidade de criar
uma escala termométrica padrão que se adaptasse bem a sociedade com intuito de
facilitar e esclarece a interpretação em relação a mesma.
2.0 MEDIDA DE TEMPERATURA:
Para definir uma escala termométrica é necessário estabelecer e associar um
conjunto de regras para um sistema. Uma maior fixação de uma escala termométrica
se inicia com a escolha de um termômetro. Com a escolha de tal instrumento, pode-se
definir e/ou adotar as propriedades, as quais se apropriem ao modelo do termômetro
escolhido.
Por volta da segunda metade do século XX, o químico Francis Giauque sugeriu
uma equação do tipo (t = a.X), que associou bem aos dados, valores correspondentes
para t., e que mais tarde foi adotada oficialmente. É bom lembrar que a escolha dessa
equação é inteiramente arbitrária, e existem outras escalas que podem exigir
equações mais complicadas para definir suas propriedades termométricas.
Com o objetivo de estabelecer uma escala empírica de temperatura, tomou-se
como padrão as coordenadas aleatórias do tipo “X e Y” do gráfico das isotermas que
está contido na figura 1, e foi estabelecido um conjunto de regras para se determinar
cada uma destas isotermas, um número. Para qualquer sistema que esteja em
equilíbrio térmico com este, o número é o mesmo.
4
Figura 1: motra a isoterma à temperatura do ponto triplo da água.
O procedimento mais adequado é a escolha da trajetória que seja conveniente
para o plano XY, a qual intercepta as isotermas em pontos que tenha a mesma
coordenada Y, mas uma coordenada X diferente. A temperatura associada a cada
isotermas é então tomada para ser uma junção conveniente de X neste ponto de
interseção. A coordenada X é denominada como propriedade termométrica e a forma
da função
(X) que determina a escala de temperaturas.
Alguns termômetros listados na tabela 1 a seguir, como exemplo, apresentam
algumas propriedades termométricas.
Tabela 1 - alguns exemplos de termômetros e propriedades termométricas:
Termômetro
Propriedade
Símbolo
termométrica
A gás
Pressão
P
Resistência elétrica
R’
Radiação
Emitância radiante
RB,
Termopar
Força
(tensão constante)
térmica
(volume constante)
Resistor elétrico
(tensão constate)
eletromotriz
5
A função da escala de temperatura na figura 1 é:
(X) = a*X
(Y constante) (1.0)
Deduz-se, segundo o que pode ser observado na figura 1, que a razão entre
duas temperaturas é:
(X1) ÷ (X2) = X1÷ X2
(1.1)
A temperatura (X) de um sistema pode ser obtida adotando-se qualquer um dos
procedimentos abaixo:
1. Método utilizado antes de 1954. Utiliza-se a equação (1.1) para um
termômetro colocado inicialmente em um sistema cuja temperatura (X) se quer medir
e depois colocado num sistema arbitrário escolhido com temperatura (X1).
Então:
(X1) ÷ (X) = X1 ÷ X .
(1.2)
Depois o termômetro é colocado em contato com outro sistema escolhido de
temperatura (X2). Portanto:
(X2) ÷ (X) = X2 ÷ X .
(1.3)
Da subtração da eq. (1.3) e (1.2), tem-se:
[( (X1) - (X2)) ÷ (X)] = [X1 - X2] ÷ X.
e
(X) = [ (X1) - (X2)]*X ÷ ( X1 - X2)
(Y constante, figura 1)
Ao intervalo (X1) - (X2), atribui-se um valor arbitrário de “graus”. (X). Pode
ser então calculado tendo X, X1 e X2.
2. Método posterior a 1954. Neste método há apenas um ponto fixo, que é o ponto
triplo da água. Neste ponto coexistem em equilíbrio gelo, água e vapor de água,
conforme a figura 2 a seguir. O ponto triplo da água é o ponto definido como padrão
6
para a termometria e o seu valor foi escolhido arbitrariamente para ser de: 273,16 K.
Para este valor fixo:
(X) ÷ (X3) = X ÷ X3 , com
(X3) = 273,16 K.
Portanto:
(X) = 273,16*(X ÷ X3) (Y constante)
(1.4)
“Os valores numéricos não pretendem ser exatos, e em lugar de
273,16 se escreveu simplesmente 273. Se as colunas
forem
comparadas, pode ser visto que os termômetros diferem em
qualquer ponto fixo, exceto no ponto triplo da água. Mesmo os dois
termômetros de hidrogênio diferem ligeiramente, porem a variação
entre termômetros de gases podem ser grandemente reduzida pelo
uso de baixas pressões, razão pela qual se escolheu um termômetro
de gás como padrão em termos do qual é definida a escala empírica
de temperatura” (ZEMANSKY, 1978, p.12-13).
A célula é resfriada até que gelo, água e vapor de água estejam presentes e em
equíbrio. A temperatura é 273,16 Kelvin por definição. Um termômetro pode ser
calibrado inserindo-o na parte central do tudo como mostra na figura 2 a seguir:
Figura 2. célula do ponto triplo da água.
Fonte: (http://www.fisica.uel.br/atomol/3pt.html)
Alguns exemplos de escalas termométricas:
Escala Celsius: é definida como sendo a centésima parte da distância entre o
ponto de fusão e o ponto de ebulição da água. A escala Celsius, como é conhecida
hoje, foi aprovada no IX Conferência Internacional de Pesos e Medidas no ano de
1948.
Fusão (f) = 0 °C
7
Ebulição (e) = 100 °C
tc = 100. (X – Xf) ÷ (Xe – Xf)
Escala Réaumur:
Fusão (f) = 0
Ebulição (e) = 80
tR = 80. (X – Xf) ÷ (Xe – Xf).
Escala Fahrenheit:
Fusão (f) = 32
Ebulição (e) = 212
tF = 80. (X – Xf) ÷ (Xe – Xf) + 32
Figura 3. As escalas termométricas.
8
Escala Kelvin:
O físico britânico William Thomson, por muitos anos de pesquisas, tentou achar o
ponto mais baixo que a temperatura pudesse alcançar. Através das suas observações,
o físico W. Thomson observou experimentalmente a variação da pressão de um
determinado gás a volume constante, então, ele concluiu com base em muitos
cálculos matemáticos que a mais baixa temperatura que o determinado gás poderia
atingir corresponderia o anulamento da sua pressão.
W. Thomson definiu esse ponto de pressão nula como o ponto zero da
temperatura ou estado de zero absoluto da termodinâmica que o corresponde a –
273,15 K. Veja com está representada na figura 4 a seguir:
Figura 4. Ponto de pressão nula.
Fonte: (http://www.ajc.pt/cienciaj/n20/hciencia.php)
A extrapolação chega ao limite e mostra que, nessa condição de baixa pressão,
todos os gases apresentam o mesmo comportamento, ou seja, comportamento de um
gás ideal.
Por essa realização e contribuição científica, o físico britânico W. Thomson, foi
excepcionalmente agradecido pelo Rei com o título de Lorde em 1892, passando a se
chamado de Lord Kelvin.
“Valor é impossível de ser alcançado, por ser puramente teórico:
pressão e volume de um gás seriam nulos a esta temperatura o que
corresponderia a uma aniquilação da matéria”! Além disso, nessas
condições todas as substâncias encontrar-se-iam já no estado
sólido, e não gasoso. A temperatura mais próxima, atingida até ao
momento, dista apenas de 1 nK (10-9 K) do zero absoluto. A título de
9
exemplo, o hélio, que é, de todas as substâncias, a que tem ponto de
ebulição e de fusão mais baixo, solidifica a 0,95 K. Assim, o valor de
-273,15 ºC é denominado zero absoluto teórico.
A escala correspondente também é conhecida por temperatura
termodinâmica, já que foi confirmado pela 2ª Lei da Termodinâmica”
Fonte: http://www.ajc.pt/cienciaj/n20/hciencia.php
2.1 Definição da unidade de temperatura termodinâmica no Sistema
Internacional SI.
Como pode ser notado, a unidade Kelvin é a fração 1/ 273,16 da temperatura
termodinâmica do ponto triplo da água. Em 1967, no XIII Conferência Geral de Pesos
e Medidas, essa unidade ou definição foi aprovada, mas deve-se ter em mente que
essa unidade não é adequada para o uso diário.
3.0 TERMÔMETROS:
3.1 Termômetro de líquido em vidro:
No termômetro de líquido uma importante propriedade termométrica é a altura da
coluna de líquido em um capilar. E o mais usado é o termômetro de mercúrio, por
apresentar algumas características que facilitam sua identificação.
O mercúrio se dilata de maneira uniforme e apresenta-se sempre no estado
líquido em intervalo de temperatura de – 38°C a 360°C. Ele é encontrado na natureza
em excelente estado de pureza, sendo uma substância densa e opaca que facilita sua
leitura dentro do vidro que compõe o termômetro.
“O mercúrio não molha o vidro, isto é, não deixa resíduos aderentes
no vidro, de modo que a massa de mercúrio que participa das
medições permanece constante, podendo-se dotar o instrumento de
uma escala que permita a leitura direta da temperatura. São usados
freqüentemente os termômetros de álcool. Neste caso utiliza-se uma
substância corante entre o álcool e o vidro” (PAULI, 1979, p. 3-13).
O termômetro de líquido que utiliza álcool tem um problema, pois o uso do
corante vai adquirindo, com o tempo, manchas nas paredes do instrumento, fazendo
com que o instrumento se torne inútil.
10
3.2 Termômetro clínico:
É aquele termômetro freqüentemente usado nas farmácias e em casa para
medir a temperatura do corpo humano. Sua escala termométrica compreende valores
de pequenos intervalos, de 35°C a 45°C.
De acordo com a figura 5 a seguir, podemos observar o seu funcionamento, o
capilar apresenta uma pequeníssima extremidade. Podemos observar que, conforme a
temperatura aumenta, o mercúrio se dilata, atravessando seu estrangulamento até
chegar à temperatura no ponto máximo. O mercúrio no interior do termômetro se
afaste do sistema que estava contido, sua medida permanece inalterável, e para
retornar ao seu ponto inicial é só agitar rapidamente fazendo com que o mercúrio
retorne passando pelo estrangulamento.
Figura 5. Termômetro clínico analógico:
Fonte: (http://cgi.ebay.it/Termometro-Clinico)
3.3 Termômetro de Six:
O termômetro de máximo e de mínimo, criado por James Six, é representado
pela figura 6, a seguir. Os bulbos no seu interior contêm álcool e mercúrio. Nos
capilares existem os filetes que ficam com os dois indicadores de ágata. Conforme
houver elevação de temperatura, o mercúrio dentro dos tubos arrasta o indicador, e
quando a temperatura diminui ocorre a contração do mercúrio, fazendo com que o
indicador seja abandonado, ficando na posição de maior elevação da temperatura, ou
seja, ficando onde teve início a contração enquanto o álcool passa livremente por ele.
Com uma suposta elevação da temperatura, há uma expansão do álcool dentro do
11
tubo, e conseqüentemente uma compressão no bulbo A e, mais embaixo na coluna C,
há um avanço empurrando o marcador até a posição que conseqüentemente
corresponde à temperatura máxima alcançada. E, por outro lado, quando há uma
diminuição na temperatura, o álcool do bulbo B se contrai fazendo com que a coluna D
arraste o indicador à temperatura mais baixa.
Figura 6. Termômetro de Six.
3.4 Termômetro Registrador de Richard:
Diferentemente do termômetro de Six, que é de máximo e mínimo, é interessante
conhecer também o termômetro registrador de Richard, no qual a variação de
temperatura é registrada em papel. Esse termômetro é envolvido por um cilindro e
dotado por mecanismo de relógio.
O termômetro registrado de Richard é freqüentemente usado em institutos de
metereologia e em aeroportos. Uma espécie de tacógrafo, que registra a variação de
temperatura ao longo dos dias da semana. Veja o modelo desse termômetro na figura
7 a seguir.
12
Figura 8. Termômetro registrador:
Fonte: (www.sbfisica.org.br)
3.5 Termômetro a Gás:
Os termômetros a gás encontrados no mercado podem ser à pressão constante
ou a volume constante. Não há muitas diferenças na sua construção e, sim, no seu
manuseio.
A figura 8 a seguir representa um termômetro a gás a volume constante.
Conforme podemos observar, o bulbo que recebe o gás é ligado ao um tubo em
formato da letra U, por um capilar. Na parte inferior da ampola, conforme podemos
observar no lado esquerdo do tubo, existe um indicador que mostra o nível de
mercúrio que permitirá fazer com que um determinado gás ocupe o mesmo volume em
todas as suas aplicações.
Figura 8. Termômetro a Gás:
13
O bulbo que está contido com gás é aproximado a um sistema que contém gelo
– água sob uma pressão normal para estabelecer um equilíbrio térmico. Com isso, a
válvula A é aberta, o reservatório é levantado ou abaixado de maneira que permite a
entrada ou saída do componente mercúrio que está no tubo em forma de U, nivelando
a superfície na ampola com o índice I, conforme está na figura. De acordo com a
escala proposta no instrumento, podemos determinar o desnível de “hG”, e com auxílio
da expressão abaixo podemos calcular a “PG” e substituir na equação térmica para
determinar a temperatura do material que estamos medindo. A relação entre
expressão e equação é:
1. PG = Patm ± .g.hG ou PV = Patm ± .g.hV => cálculo da pressão.
2. tc = 100 * [(P- PG) / (PV- PG )] => cálculo da temperatura em graus Celsius.
Observação: aplica-se o sinal positivo (+) na expressão 1. quando o desnível está
sobre o nível do mercúrio na ampola, e o sinal negativo (-), quando o desnível está sob
o nível da ampola.
Para realizar a mesma medida, agora em volume constante, vamos realizar o
mesmo procedimento usado com pressão constante. Em volume constante, o bulbo
que contém o gás é elevado à presença de um sistema água – vapor sob pressão
normal. Estabelecido o equilíbrio térmico entre o sistema, abre-se novamente a válvula
A, e o reservatório é deslocado fazendo com que o mercúrio que está na ampola
retorne ao seu índice de referência I.
Quando desejar que o termômetro opere à pressão constante, é só substituir o
índice que está contido no referencial I, e adaptar a ampola em uma escala
volumétrica. Com a ajuda de uma escala termométrica fixada no próprio termômetro,
registramos um desnível “h” que está presente nas duas operações que o termômetro
a gás realiza, permanecendo à pressão constante que é dada pela expressão P = Patm
± .g.h. Com isso, podemos ler a operação que o volume de um gás ocupa na escala
contida na ampola. Utilizando uma escala termométrica para auxiliar as medidas,
temos uma escala em Celsius:
tc = 100. (V – Vg) ÷ (Vv – Vg)
__________________
As siglas que estão no sob escrito das letras são: “G” de gelo e “V” de vapor.
14
3.6 Termômetro de Resistência Elétrica:
A resistência elétrica de um resistor elétrico revela-se em experiências em que
o mesmo varia com a temperatura, adquirindo propriedades termométricas. O
termômetro de resistência elétrica tem aparência de um fio fino e longo. Usualmente
enrolado em volta de um quadro, o termômetro é construído de forma a evitar
excessivas tensões quando há contração do mesmo pelo seu resfriamento. Quando o
termômetro é direcionado para medir baixas temperaturas, ele geralmente é formado
por pequenos resistores de rádios no qual a base é carbono ou cristal de germânio,
que é selado por uma cápsula que contém no seu interior gás hélio.
Podemos fazer uma medida com este termômetro, conservando a corrente
constante, que foi definida na calibração do mesmo, e determinando a diferença de
potencial entre seus extremos por auxílio de um potenciômetro de alta sensibilidade.
Já o termômetro de resistência de platina tem autonomia para trabalhar em
grandes intervalos de temperaturas que variam de – 253°C a 1200°C. A calibragem do
instrumento é feita por meio de medida de R’pt, que pode ser obtido através da
representação de uma fórmula empírica.
A fórmula representada abaixo é uma conseqüência da equação quadrática:
R’pt = Ro * (1 + A.t2+ B.t)
Figura 9. Circuito de um termômetro de resistência elétrica.
_______________
R’pt é definido com resistência no ponto triplo da água, e Ro é a resistência do fio de platina. A e
B são constantes.
15
3.7 Pirômetro:
O nome “piro” tem origem do grego (pyro, fogo). Esse é um instrumento de alta
sensibilidade à radiação eletromagnética na faixa do infravermelho, que pode ser
utilizado para medir temperaturas acima dos pontos de fusão dos metais. Esse
instrumento foi sugerido no primeiro momento por Antoine Becquerel em 1852, e
praticamente quarenta anos mais tarde foi colocado em prática por Henri Louis Lê
Châtelier, em 1892, que revela o primeiro modelo desse instrumento, conhecido como
pirômetro óptico. Somente em 1931 os pirômetros chegam aos estabelecimentos
comerciais.
O pirômetro é um instrumento bem diferente na aparência e na sua utilidade de
um termopar. O pirômetro óptico não tem necessidade de manter ou ter contato físico
com o instrumento, como os pares termoelétricos. Ele pode atuar na faixa de radiação
eletromagnética do visível e também na faixa de radiação eletromagnética do
infravermelho. O instrumento apresenta um método diferente para realizar suas
medidas. Esse método consiste na comparação entre as radiações eletromagnéticas
dos corpos. Todos os corpos emitem radiações eletromagnéticas, e essa energia
radiante, ou irradiante, é medida por comparação fotométrica por diferentes
comprimentos de ondas emitidos pelo corpo, que é medido em relação à cor padrão
da fonte.
A comparação entre os comprimentos de ondas é realizada pelo próprio
observador, que distingue a diferença entre os comprimentos de ondas que aparecem
entre as superfícies. Para realizar uma operação com pirômetro óptico é necessário
contar com o auxílio de um filtro monocromático de cor vermelha. Com isso, podemos
realizar nossa medida fazendo uma comparação entre o comprimento de onda padrão,
variando a corrente do filamento de tungstênio que está contida na fonte, até que a
mesma se iguale com o comprimento de onda captado pelo corpo radiante.
16
Figura 10. Pirômetro.
Fonte: (www.fem.unicamp.br/~instmed/Temperatura_2.pdf)
Para haver a necessidade de utilizar um pirômetro óptico, o corpo radiante
deve estar a uma temperatura mínima de 750°C. Assim, pode-se fazer medidas de
alta temperatura utilizando-o, o qual pode ter um alcance máximo de temperatura
próxima de 5500°C, com auxílio de um anteparo absorvente.
O pirômetro coleta radiação eletromagnética entre a faixa do visível e a faixa do
infravermelho e mede a taxa de emissão de energia por unidade de área, através de
um detector que converte em pulsos (sinais) elétricos. Todos os corpos que contêm
uma temperatura superior a zero Kelvin emitem energia, e à medida que a
temperatura do corpo (objeto) aumenta por um “fator T4”, esse fator nos permite
realizar medições de temperatura com precisão de qualquer objeto radiante através da
energia emitida.
“A energia irradiada por um corpo depende, de fato, da emissividade
( ) da sua superfície. Ela é máxima para um corpo negro ( = 1). Os
pirômetros são calibrados em relação a um corpo negro, e um fator
de correção deve ser empregado quando a medição é realizada em
um corpo com emissividade diferente. Para isso deve-se conhecer a
emissividade da superfície que está sendo medida, o que é um fator
de incerteza, visto que a emissividade varia com o estado da
superfície, temperatura e etc. outro fator de incerteza na medição de
corpos com emissividade inferior a 1 (um) diz respeito à influência
dos corpos vizinhos: a radiação emitida por um corpo vizinho pode
17
vir a ser refletida na superfície de medição e atingir o sensor,
falseando a medição” (Termometria nos séculos XIX e XX, 2006).
Os pirômetros são diferenciados pelos tipos de detectores, sendo:
•
Térmico: que é responsável por responder à energia contida na onda
eletromagnética do espectro eletromagnético e possui um tempo de
resposta relativamente grande.
•
Fótons: a radiação eletromagnética incidente libera elétrons na estrutura
do detector e gera um efeito elétrico, que pode ser medido através de
um sensor, e também apresenta uma constante de tempo na ordem de
um mili-segundo.
Figura 11. Pirômetro óptico:
Fonte: http://www.spectrodyne.com/DFP2000
4.0 PARES TERMOELÉTRICOS:
Graças às pesquisas, sabe-se que o uso de líquidos como sensores de
temperatura é limitado pelo seu ponto de ebulição, daí surgiu a necessidade de se
desenvolver novos sensores que pudessem determinar a variação da temperatura, os
quais pudessem suportar temperaturas superiores às de todos os pontos de ebulição
dos líquidos utilizados nos termômetros.
Novos instrumentos foram desenvolvidos para suprir essa necessidade, estes
instrumentos são conhecidos como pirômetros e pares termoelétricos.
18
Para se construir um par termoelétrico dobra-se dois metais de maneira que os
mesmos formem um anel aberto, colocando-se as pontas dos metais em contato uma
com a outra estabelece-se a mesma tensão de contato. As duas tensões estarão
interligadas em oposição uma à outra, com isso, não há fluxo algum de corrente
térmica entre os mesmos. Mas se escolhermos uma das pontas e aquecê-la, as duas
extremidades de contato terão comportamentos diferentes, isso fará com que surja
uma corrente térmica no sistema. Porém, se soldarmos fios metálicos de diferentes
materiais, e aplicarmos um voltímetro entre suas extremidades, o instrumento acusará
uma tensão elétrica, devido às propriedades de cada metal e também à diferença de
temperatura entre os pontos que estão contidos as soldaduras. Deixando uma
soldadura em temperatura constante, por exemplo, em uma mistura de água-gelo, terse-á no sistema um termo-elemento com propriedades de um termômetro, que
apresenta grande vantagem, grande sensibilidade e pequena capacidade calorífica.
Esse termo-elemento dispõe de várias combinações metálicas que respondem
às mesmas propriedades termométricas de um termômetro, o qual é conhecido como
termopar. As combinações mais simples e mais encontradas, atualmente, nos
laboratórios e nos mercados são de cobre e constantan, e de ferro e constantan.
(Constantan => Liga metálica para resistores elétricos, de 60% de cobre e 40% de
níquel).
O físico alemão Thomas Johann Seebeck, entre os séculos XVIII e XIX,
verificou que unindo as pontas de dois fios metálicos diferentes “X” e “Y” (figura 13) e
submetendo-as às extremidades “a” e “b” a temperaturas diferentes “T1” e “T2”,
aparecerá uma força eletromotriz de Seebeck (f.e.m), a qual é normalmente da ordem
de milivolts, denominada tensão termoelétrica.
19
Figura 12. Dois metais diferentes, “x” e “y” com as extremidades unidas e mantidas a
temperatura diferentes.
Fonte: http://www.ucs.br/ccet/demc/vjbrusam/inst/UCS08.pdf
Observação: “T2” igual à temperatura ambiente.
O efeito de Seebeck, como é conhecido, nos mostra que se dois fios metálicos
de diferentes materiais nas junções “a” e “b” que foram mantidos em temperatura
diferentes “T1” e “T2” como mostra na figura 12, forem conectados, aparecerá no
sistema uma f.e.m (força eletromotriz) termoelétrica e uma corrente elétrica “i” que
circulará no termopar.
Ao abrir o circuito que forma a estrutura de um termopar para inserir um
instrumento que possa medir a força eletromotriz, o voltímetro, (figura 13), que
normalmente está na ordem de m.V., se uma das temperaturas das junções for
conhecida, pode-se, através da f.e.m produzida, descobrir-se o valor da temperatura
da outra junção.
20
Figura 13. Abrindo o circuito em qualquer ponto e inserindo um instrumento adequado, tem-se
o valor da f.e.m.
Fonte: http://www.ucs.br/ccet/demc/vjbrusam/inst/UCS08.pdf
As medições de temperaturas são, na realidade, as maiores aplicações do
termopar (que também pode ser usado como conversor termoelétrico, embora
apresente baixo rendimento), bastando para isso que se conheça a relação f.e.m.
versus a variação de temperatura na junção do termopar. Esta relação pode ser
conseguida através de uma “calibração”, ou seja, uma comparação com um padrão.
O instrumento desenvolvido em 1886 por Henri Louis Le Châtelier, que é
formado por ródio/ platina, mereceu destaque por muitos anos, por ser o instrumento
de interpolação das escalas internacionais de temperatura superior a 600°C e hoje, é
padrão secundário de diversos laboratórios.
“Deve-se ter um cuidado todo especial com a junta de referência
(chamada às vezes de junta fria), uma vez que a flutuação de sua
temperatura pode acarretar erros nas aplicações práticas dos
termopares. Assim sendo, procura-se manter a junta de referência
em locais onde ocorrem pequenas flutuações de temperatura; no
passado, usava-se com referência a temperatura de 0°C. Na
atualidade, os voltímetros que medem a f.e.m. de termopares
dispensam esta junta de referência, pois têm circuitos que
compensam eletronicamente o fato de a temperatura ambiente não
ser 0°C” (Termometria nos séculos XIX e XX, 2006).
21
Então, nota-se que quando é colocada uma das juntas soldadas do par
termoelétrico em um ambiente onde se deseja medir a temperatura “T1”, que é
conhecida como “junta quente” e na outra extremidade “T2” chamada de “junta fria”,
aparecerá uma diferença de potencial (d.d.p) entre os extremos do sistema. Esta
tensão como já foi citada anteriormente, é da ordem de milivolts, e o valor encontrado
varia linearmente devido à expressão seguinte: V = K (T1 – T2), em que “K” é uma
constante termoelétrica que depende dos materiais (fios) componentes do termopar.
Essa variação linear que aparece no sistema depende das diferenças de temperaturas
entre as duas extremidades do instrumento termoelétrico e a escolha dos materiais
que compõem os instrumentos depende do grau da sua necessidade para o
manuseio.
Termopares Comerciais: a principio, um termopar pode ser confeccionado com
dois metais diferentes quaisquer; entretanto, devido a uma série de fatores
(contaminação, custos, repetibilidade, ponto de fusão, homogeneidade, facilidade de
produção, fácil soldagem, etc.), são oferecidas poucas combinações no comércio.
Dentre os termopares comerciais pode-se observado na tabela 3 a seguir:
Tabela 2. Veja alguns exemplos de termopar e suas utilidades na sociedade.
TERMOPAR
Faixa de uso
aconselhada
Algumas
Aplicações
J
Ferro –
Constantan
(-190 a 870) °C
K
Cromel – Alumel
(-18 a 1370) °C
1- Têmperas
2- Recozimento
3- Fornos
elétricos
1- Tratamento
térmico
2- Fornos
3- Fundição
4- Banhos
T
Cobre –
Constantan
(-190 a 370) °C
1- Estufas
2- Banhos
3- Fornos
elétricos
para baixa
temperatura.
Vantagens
Desvantagens
1- Baixo custo
1- Devem ser
usados tubos de
proteção para T >
480 °C.
1- vulnerável a
atmosferas
redutoras.
1- Adequado
para
atmosferas
oxidantes.
2- Boa
resistência
mecânica em
altas
temperaturas.
1- Resiste a
1- Oxidação do
atmosferas
cobre acima de 315
corrosivas.
°C.
2- Resiste a
atmosferas
redutoras e
oxidantes.
22
R – Pt – Pt 13%
Rh S – Pt – Pt
10% Rh.
(-18 a 1540) °C
3- Utilizável em
temperaturas
negativas.
1- Pode operar
em atmosfera
oxidante.
2- Opera numa
faixa
superior o
termopar tipo
K.
1- Vidros
2- Fornos (T >
1300 °C)
3- Fundição
4- Alto – forno
1- Contamina
facilmente
em
atmosfera
não
oxidante.
2- Fragiliza
em alta
temperatura
Fonte: www.ucs.br/ccet/demc/vjbrusam/inst/UCS08.pdf
4.1 Fenômenos termométricos:
Sabemos que, quando dois metais de diferentes composições químicas são
conectados, as junções são mantidas em uma diferença de temperatura e em ambos
os
pontos
ocorrem
simultaneamente
o
aparecimento
de
cinco
fenômenos
termoelétricos:
1.
Efeito Joule: Se a força eletromotriz térmica não é contrabalanceada por
uma f.e.m externa, temos origem de uma corrente de intensidade “i” devido seu valor,
que pode ser ajustado variando a f.e.m externa. Enquanto existir uma corrente
térmica, dissipar-se-á dentro do circuito, uma energia elétrica .
2.
Efeito Fourier: temos em mente agora um sistema termoelétrico cujas
junções se encontram em respectivas temperaturas, “T1” e “T2” em que as mesmas
são diferentes (T1 maior do que T2). Desse modo, as junções são interrompidas por
um ponto no sistema, mantendo agora as extremidades a mesma temperatura. Se “T1”
tem maior temperatura, a mesma perderá calor e “T2” ganhará calor para haver
equilíbrio entre ambas. Então, nessa condição de equilíbrio, não temos corrente
térmica no sistema, também não há efeito Joule por conseqüência da ausência de
corrente elétrica.
3.
Efeito de Seebeck: esse efeito é produzido pelo fato de que a densidade
dos transportadores de cargas, que são os elétrons em um determinado metal, diferese de um condutor para outro e depende da temperatura. Quando dois materiais de
diferentes ligas metálicas são conectados para formar duas junções, e essas junções
são colocadas a diferentes temperaturas, a propagação dos elétrons nas junções é
produzida a ritmos diferentes, tendo origem em um movimento líquido dos
23
transportadores de carga como se fossem impulsionados por um campo não
eletrostático. Este efeito descreve a produção de uma força eletromotriz (f.e.m.) num
circuito que contém dois metais diferentes, quando as junções entre os dois são
mantidas a temperaturas diferentes. O valor da f.e.m. depende da natureza dos metais
e da diferença de temperaturas.
A tensão que existe no circuito entre as junções é denominada de tensão de
Seebeck e essa tensão aumenta à medida que a diferença de temperatura entre as
junções aumenta.
4.
Efeito Peltier: temos um termopar com as suas junções à mesma
temperatura, se adaptarmos a ele uma bateria externa, a mesma produzirá uma
corrente no par termoelétrico e as temperaturas das junções variaram em uma
quantidade não inteiramente devida ao efeito Joule. Essa variação adicional de
temperatura denomina-se efeito Peltier. Esse efeito é produzido, portanto, pela
corrente proporcionada por um manancial externo como pelo próprio termopar.
Resultados obtidos pelo efeito Peltier:
o
A quantidade de calor Peltier produzida por unidade de tempo é
proporcional à primeira potência da intensidade da corrente, ou seja, é
igual a
.i. a grandeza
é chamada de coeficiente Peltier e é igual ao
calor transferido quando uma quantidade unitária de eletricidade
atravessa a junção.
o
O calor Peltier é reversível. Quando se inverte o sentido da corrente,
permanecendo constante seu valor, o calor Peltier é o mesmo, porém
de sentido oposto.
o
O coeficiente Peltier depende da temperatura e dos metais que formam
uma junção, sendo independente da temperatura da outra junção.
o
Convencionou-se considerar
AB
como positivo quando uma corrente
elétrica de A para B provoca uma absorção de calor pela junção.
5.
Efeito Thomson: a condução de calor dentre os fios metálicos de um
sistema termoelétrico que não transporta corrente, origina-se em uma distribuição
uniforme de temperatura em cada fio do termopar. Quando existir corrente em ambos
os fios, terá também diferentes distribuições de temperaturas em cada ponto em uma
quantidade não inteiramente devida ao efeito Joule.
Para medir o chamado calor Thomson em um determinado ponto ou região de
um fio metálico, há a necessidade de produzir um gradiente de temperatura na região
referida, e fazer com que se passe uma corrente com uma determinada intensidade,
aumentando ou diminuindo o gradiente. É bom saber que, se for possível calcular o
24
efeito Joule e o calor conduzindo como na experiência prever, é também possível
saber e determinar o calor Thomson.
Resultados obtidos pelo efeito Thomson:
•
A quantidade de calor Thomson produzida por unidade de tempo em
uma pequena região de um fio metálico, que transporta uma corrente “i”
e suporta uma diferença de temperatura dT, é igual a .i.dT, sendo
o
chamado coeficiente Thomson.
•
O calor Thomson é reversível.
•
O coeficiente Thomson depende do metal de que é feito o fio e da
temperatura média da pequena região considerada.
•
Convencionou-se considerar
positivo quando uma corrente de sentido
oposto ao do gradiente de temperatura (de baixa para alta temperatura)
produz uma absorção de calor pelo condutor.
5- MATERIAIS E MÉTODOS:
5.1. Materiais necessários:
• Multímetro digital (ET- 2700).
• Interface da PASCO
(science workshop 750).
• Sensor de temperatura
TYPE “K” da PASCO.
• Fios (cabos) para conexões.
• Microcomputador.
• Fita adesiva.
• Garrafa térmica
• Tubo de ensaio com areia.
• Termômetro de mercúrio.
• Copo de papel alumínio com areia.
• Bico de bunsen.
• Óculos de proteção industrial.
• Manta aquecedora.
• Pedestal (tripé).
• Pares termoelétricos (cobre e ferro) e
(cobre e constantan).
• Software Data Studio.
• Software Maple.
25
5.2. Procedimento:
A montagem experimental ocorreu conforme mostra a figura 14 a seguir,
seguindo o esquema termoelétrico proposto pela figura 15.
Figura 14. Montagem do circuito termoelétrico:
Fonte
quente
Fonte
fria.
Voltímetro e a
abaixo interface
da Pasco.
Sensor de
temperatura
da Pasco.
Figura 15. Foto da montagem do circuito termoelétrico:
26
Nota-se que uma das extremidades do par termoelétrico está o máximo
possível mergulhada na areia e no mesmo nível do sensor de temperatura. Observe
que a areia está no tubo de ensaio que, por sua vez, está mergulhado em um copo
feito de papel de alumínio com areia suspenso sobre um bico de bunsen, fonte quente.
A outra extremidade do termopar deve está o máximo possível imersa dentro
de uma garrafa térmica, contendo gelo e água para manter essa extremidade a uma
temperatura de 0°C. O multímetro é responsável para medir a f.e.m do termopar e o
sensor de temperatura da Pasco é responsável pela transferência das informações da
temperatura (°C) para a interface da Pasco. O software Data Studio é utilizado na
leitura e armazenamento dos dados coletados
A partir do momento em que o bico de bunsen for aceso (fonte quente) deve-se
começar a anotar os valores da temperatura em função da voltagem (f.e.m) até uma
temperatura limite (550°C).
5.3 Medidas Realizadas:
Na figura 16 apresentam-se as medidas experimentais para o termopar
Cobre – Constantan e na figura 17 para o par termoelétrico Ferro – Cobre. Nas
duas figuras, temos para o eixo Y = f.e.m em volts e no eixo X = temperatura
em graus Celsius. Os resultados apresentados se referem ao resfriamento. Os
resultados para o aquecimento foram análogos, mas como o aquecimento é
rápido, as medidas do resfriamento são mais confiáveis.
27
Figura 16. Cobre e Constantan:
Figura 17. Ferro e Cobre:
28
5.4. Analise dos resultados:
Se uma das extremidades do par termoelétrico “Ferro – Cobre” for conservada
a uma temperatura que pode ser chamada de referência Tr = 0°C, e a outra
extremidade for aquecida progressivamente, pode-se notar que a força eletromotriz
chega a um valor máximo de 298,4 graus Celsius (ponto neutro), e se continuar
aumentando a sua temperatura, pode-se constatar que a f.e.m de Seebeck começará
a descer, descrevendo uma trajetória parabólica (função quadrática) até atingir um
valor próximo de zero volt (V) a uma temperatura de 601,7°C (extrapolação do gráfico
na figura 18). A partir desta temperatura a força eletromotriz “E” inverte o sinal e é
chamada de temperatura do ponto de inversão (Ti).
Figura 18. Ferro – Cobre. As mesmas medidas da figura 19, mais o gráfico feito no software
maple.
Pode-se notar, a partir do observado na figura 18, que para termopares de ligas
metálicas diferentes, a curva não será necessariamente igual, porque cada par
termoelétrico tem suas características devido a sua composição metálica. E essa
curva é característica da composição entre, cobre - ferro. Os cálculos realizados
referentes aos valores teóricos e experimentais dos termopares Ferro – Cobre e Cobre
– Constantan (figuras 18 e 19) estão disponíveis no anexo. Veja o termopar de Cobre
– Constantan.
29
Figura 19. Cobre – Constantan.
Já o termopar Cobre – Constantan apresenta um comportamento bem
diferente, praticamente linear no intervalo de 0 – 550 graus Celsius. Nesse par
termoelétrico não temos o ponto neutro e nem o de inversão, o que pode ser
observado, todavia, pela concavidade no gráfico subindo “praticamente linear”.
Os resultados experimentais e a teoria sobre termopares mostram que a
variação da força elétrica de Seebeck com a temperatura é compatível com o modelo
quadrático representado abaixo:
[ F.E.M = ½ A.T2 + B.T + C ]
Se a temperatura de referência (fonte fria) for igual a zero grau Celsius (0°C),
temos uma das constantes igual à zero, ou seja, C = 0 V. evidentemente, se a
temperatura de referência for diferente de zero, temos: C
0 m.V.
As constantes “A e B” são responsáveis pela definição da aferição do termopar.
Com isso, é importante saber que, se a temperatura da fonte fria (Tr) for maior do que
zero grau Celsius, a temperatura do ponto de neutro continua a mesma, mas a
temperatura do ponto de inversão é reduzida. Também deve ser lembrado que o
processo citado depende da natureza dos metais de cada termopar.
Como citadas anteriormente, as constantes “A e B” dos metais que constituem
os pares termoelétricos podem ser adquiridas pela subtração de seus valores em
relação a outros valores que são tomados como referência (cálculos que seguem em
anexo), essa referência no geral é o composto químico platina ou o chumbo. Temos
uma tabela com as constantes “A e B” de vários metais e ligas metálicas.
30
Tabela 3: constantes de vários metais e ligas metálicas.
Metal
(referência: o chumbo)
B ( .V/ °C)
Alumínio
Cobre
Constantan
Ferro
Platina
Pt, 10% Rh
A ( .V/°C)
-17,49
0,00144
1,34
0,0094
-38,105
-0,0888
17,15
-0,048
-0,6
-0,0109
6,413
0,0064
Fonte: (VENCATO e PINTO, 1992).
Nota-se que aparecem sinais negativos na tabela. Eles foram convencionados
de tal forma que, quando a constante “B” é positiva, a corrente no circuito circula no
termopar da extremidade quente para fria. Com isso, o ajuste da curvas quadráticas
dos resultados experimentais conduz os seguintes resultados (que seguem em anexo)
para afeição dos termopares. Usa-se o chumbo com referência na equação citada:
[ F.E.M = ½ (AFePb – ACuPb). T2 + (BFePb – BCuPb) ]. T
Figura 20. Mostra os resultados do ajuste para os termopares de Ferro - Cobre e
Cobre – Constantan no software Data Studio.
31
Os resultados com os valores experimentais das constantes “A” e “B” podem ser
obtidos por meio do ajuste conforme mostra a figura 20, o qual pode ser comparado ao
valor teórico obtido na tabela 3.
6. CONSIDERAÇÕES FINAIS:
Hoje, sabe-se que o termômetro é um instrumento de bastante precisão e de
grande utilidade nas indústrias e no cotidiano da nossa população. Antigamente, esse
instrumento mostrou-se em uma evolução bastante lenta por conseqüência do
conhecimento empírico em relação aos fenômenos térmicos. Com o passar do tempo,
conseguiu-se reproduzir novos termômetros mais confiáveis e, com isso, estabeleceuse escalas termométricas mais apropriadas e adequadas para o uso prático.
Conforme observado na realização do experimento, pode-se determinar que
quando duas extremidades estão em temperaturas diferentes, a densidade de elétrons
livres propaga-se de um metal para outro.
Em referência aos pontos neutros e de inversão, pode-se concluir que nem
todos os termopares têm esses pontos característicos como pode ser observado na
figura 20. O Ferro – Cobre apresentou uma curva característica com ponto neutro e de
inversão, e o Cobre – Constantan não apresentou esses pontos distintos no intervalo
de temperatura analisado. Para termopares que têm esses pontos característicos, é
bom lembrar que os mesmos têm suas temperaturas características e valores
diferentes para constantes “A” e “B”.
As constantes citadas devem ser adquiridas como referência característica de
cada par termoelétrico, e seus valores reais dependem fortemente da pureza dos
componentes metálicos ou das proporções das ligas metálicas que as constituem, sem
esquecer das condições das junções. É bom saber que as condições químicas
presentes no meio (ácido ou básico) podem afetar desastrosamente o desempenho do
termopar, podendo torná-lo inviável o seu uso ao longo do tempo.
32
7. REFERÊNCIAS BIBLIOGRÁFICAS:
FOLMER – JOHNSON, TORENILS. OLOF. Termodinâmica, São Paulo: W. Roth e
Cia. 1977.
GERTHSEN, Chistian, VOGEL, Helmut. Física. 2.ed Lisboa: Calouste Gulbenkian,
1998, p. 317-320.
História
Medição
Temperatura,
disponível
em:
http://www.helptemperatura.com.br/html/interesse/files/.pdf ; Acesso em agosto de 2007.
PAULI, Ronald Ulysses. Física básica 1° ed. São Paulo: EPU, 1979. 4.v il.
SEARS, Francis Weston; YOUNG, Hugh D; ZENANSKY, Mark W. Física 2: mecânica
dos fluidos, calor e movimento ondulatório. 2° ed. Rio de Janeiro: Livro Técnico e
Cientifico. 1984.
Termometria nos séculos XIX e XX. Revista Brasileira de Ensino de Física, v. 28, n. 1,
p. 101 – 114, (2006). Disponível em: www.sbfisica.org.br; Acesso em agosto de 2007.
VENCATO, IVO; PINTO, ABIO. V. A. Física experimental II: Eletromagnetismo e ótica.
Florianópolis: ed. da UFSC, 1992. 4. V.
ZEMANSKY. Mark. W., Calor e Termodinâmica. ed. Guanabara Dois, Rio de Janeiro,
1978, p. 8-23 e 372-383.
8. ANEXO:
33