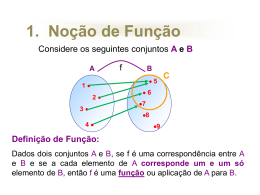
Função
Professor: Dejahyr
05/11/2015
Professor Dejahyr - 2010
Noção do conceito de função
05/11/2015
Professor Dejahyr - 2010
Definição
Toda função polinomial da forma f(x) = ax + b,
com a  0 , é dita função do 1° grau (ou função
afim).
Ex.: f(x) = 3x – 2;
a=3eb=-2
f(x) = - x + ½;
a = -1 e b = ½
f(x) = -2x;
a = -2 e b = 0
05/11/2015
Professor Dejahyr - 2010
Casos Especiais
Função linear
b = 0, ex.: f(x) = 3x
Função Identidade b = 0 e a = 1, ou
seja, f(x) = x
Função constante a = 0, ex.: f(x) = 3
05/11/2015
Professor Dejahyr - 2010
Gráficos
Todo gráfico de uma função do 1° grau é
uma reta.
Estudaremos como essa reta vai se
comportar através de cada função.
05/11/2015
Professor Dejahyr - 2010
Crescimento e decrescimento de
uma função
Uma função será crescente quando a>0
Uma função será decrescente quando a<0
Exemplo:
f(x) = 2x+1
f(x) = -3x+2
05/11/2015
a=2
a = -3
Professor Dejahyr - 2010
crescente
decrescente
Se a>o então f(x) é crescente. (a)
Se a<0 então f(x) é decrescente. (b)
y
y
a>0
a<0
5
5
x
-5
-5
5
5
-5
-5
Função crescente
Função Decrescente
(a)
05/11/2015
x
(b)
Professor Dejahyr - 2010
Função Crescente
y
f(5)
Aumenta o valor
de y
5
Função
crescente
f(2)
x
-5
2
-5
05/11/2015
5
Aumentando o valor de
x
Professor Dejahyr - 2010
Função
Decrescente
y
f(5)
Diminui o valor
de y
5
Função
Decrescente
f(2)
x
-5
2
-5
05/11/2015
5
Aumentando o
valor de x
Professor Dejahyr - 2010
Como fazer um
gráfico
1° método:
Para traçar o gráfico de qualquer função
do 1º grau, basta achar dois pontos e
passar uma reta por esses dois pontos.
05/11/2015
Professor Dejahyr - 2010
Zero da Função do Primeiro
Grau
(é o valor que anula a função f(x), isto é,
f(x)=0)
f(x)=0
a x +b = 0
a x = -b
x = (-b/a)
05/11/2015
Professor Dejahyr - 2010
Este é o valor que
anula a função f(x)
Para traçar o gráfico da função do
primeiro grau, bastam 2 pontos:

O ponto onde a função corta o eixo y

O ponto onde a função corta o eixo x
a>0
a<0
y
Ponto onde corta
o eixo y
y
5
5
Ponto onde corta o
eixo y
x
x
-5
5
-5
-5
-5
Ponto onde corta o
eixo x (raiz)
05/11/2015
5
Ponto onde corta o
eixo x (raiz)
Professor Dejahyr - 2010
Como encontrar esses dois
pontos
Ponto onde a função corta o eixo y
Basta fazer x = o, na função f(x) = a.x + b:

f(x)= a.x + b, para x = 0
f(x) = a .o + b
f(x) = b

05/11/2015
Ponto onde corta o eixo y:
Professor Dejahyr - 2010
(0,b)
Como encontrar esses
pontos
Ponto onde a função corta o eixo x
Basta fazer y = o, na função f(x) = a.x + b

f(x) = a.x + b, para y = 0
0 = a.x + b ou a.x + b = 0
x = -b/a

05/11/2015
Ponto onde corta o eixo x:
Professor Dejahyr - 2010
(-b/a,0)
ESTUDO DO SINAL
a >0 (a é positivo então a função crescente)
Valor que aula a função é (–b/a)
++++++++
---------
-b/a
f(x) = a x +b
05/11/2015
Professor Dejahyr - 2010
ESTUDO DO SINAL
a<0 (a é negativo então a função decrescente)
Valor que anula a função é (b/a)
++++++++
b/a
---------
f(x) = -a x +b
05/11/2015
Professor Dejahyr - 2010
GRÁFICO DA
FUNÇÃO
f(x) = 2x – 3
Ponto onde corta o eixo x é: (3/2,0)
Ponto onde corta o eixo y é: (0, -3)
Função crescente (a = 2 > 0)
(3/2,0)
(0,-3)
05/11/2015
Professor Dejahyr - 2010
GRÁFICO DA FUNÇÃO
f(x) = - 2x – 3
Ponto onde corta o eixo x é: (-3/2,0)
Ponto onde corta o eixo y é: (0,-3)
Função decrescente (a = -2 < 0)
(-3/2,0)
(0,-3)
05/11/2015
Professor Dejahyr - 2010
FUNÇÃO
CONSTANTE
Se na função f(x)=ax ± b, a =0 então: f(x) = ± b
Esta função é dita função constante.
f(x) = 4
f(x) = - 4
05/11/2015
Professor Dejahyr - 2010
FUNÇÃO LINEAR
Se na função f(x)=a.x ± b, b = 0 então: f(x) = ax
Esta função afim é dita LINEAR.
a>0
05/11/2015
a<0
Professor Dejahyr - 2010
Exemplo:
f(x) = x – 2
X
Y
1
-1
3
1
(2,0)
(0,-2)
05/11/2015
Professor Dejahyr - 2010
Gráfico de uma função definida por
mais de uma sentença
 x  1, se x  1
f ( x)  
2, se x  1
f ( x)  x  1, se x  1
05/11/2015
X
Y
1
2
2
3
Professor Dejahyr - 2010
Até 40h  3,00 por hora
Acima de 40h  + 50% (4,50 por hora)
Salário Bruto = (até 40h) + (acima de 40h)
Sendo x o número total de horas,
S(x) = 40.3 + (x – 40).4,5
S(x) = 120 + 4,5x – 180 = 4,5x - 60
05/11/2015
Professor Dejahyr - 2010
Fixa ...... 4,60 + 0,96 por quilômetro
Para um valor de 19,00
F(x) = 4,60 + 0,96.x
19 = 4,6 + 0,96.x
14,4 = 0,96.x
15 = x
05/11/2015
Professor Dejahyr - 2010
X – preço de tabela
À vista: (30% de desc) = 0,7.x
Cartão de crédito: 1,1.x
Logo 0,7.x = 7000
x = 10.000
E portanto, no cartão 1,1.10000 = 11000
05/11/2015
Professor Dejahyr - 2010
05/11/2015
Professor Dejahyr - 2010
05/11/2015
Professor Dejahyr - 2010