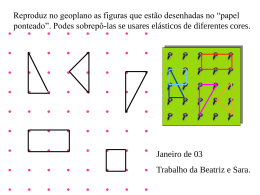
Universidade Tecnológica Federal do Paraná - UTFPR
Programa de Pós-Graduação em Ensino de Ciência e Tecnologia - PPGECT
Padrões de simetria e o Geoplano
Rosemeire Bressan
Resumo
A simetria ensinada no ensino fundamental e médio pode ser aprofundada
com o uso do Geoplano, material de fácil utilização e que também pode ser
aplicado no ensino de Matemática. Exemplos de algumas construções são
mostrados neste trabalho, visando a incentivar os alunos a construírem seus
padrões, seguindo a criatividade de cada um e modificando-os a qualquer
momento.
Palavras-chave: Simetria, Geoplano, Ensino de matemática.
Abstract
Patterns of symmetry and Geoboard
The symmetry taught in elementary and high school can be enhanced with
the use of Geoplana devices, easy to use and can also be applied in the teaching of
Mathematics. Examples of some buildings are shown in this work to encourage
students to construct their patterns according to the creativity of each and change
them at any time.
Keywords: Symmetry, Geoboard, Teaching of mathematics.
I Simpósio Nacional de Ensino de Ciência e Tecnologia – 2009
Página: 1112
ISBN: 978-85-7014-048-7
Universidade Tecnológica Federal do Paraná - UTFPR
Programa de Pós-Graduação em Ensino de Ciência e Tecnologia - PPGECT
Introdução
A Matemática é uma das disciplinas em que os alunos apresentam os maiores índices de
dificuldade como pode ser visto no resultado do Saresp 2007 e na Prova Brasil. No Saresp(
Sistema de avaliação e rendimento do Estado de São Paulo), 80% dos alunos do ensino
fundamental obtiveram notas abaixo do esperado e, para os alunos do ensino médio, 71% tiraram
pontuação que os classificaram no nível abaixo do básico. A Secretaria da Educação do Estado de
São Paulo dispõe, em seu site, de todos esses resultados, classificando-os por cidade, diretoria e
escola. Tendo em vista essa dificuldade, faz-se necessário melhorar o ensino de Matemática. Para
o professor, que necessita transmitir conhecimentos, vale a pena tentar maneiras diferentes e
agradáveis, para que o aluno possa aplicar a sua criatividade e seu conhecimento.
Um material que pode contribuir com o ensino é o Geoplano. O primeiro trabalho sobre o
uso do Geoplano foi escrito pelo Dr. Caleb Gattegno em 1961. Desde então, tem sido utilizado por
muitos professores para ensinar frações, áreas, perímetros, números racionais, simetria e outros.
Ele pode ser formado por quadrados, triângulos equiláteros ou círculo. O Geoplano com
triângulos é chamado de isométrico, porém o mais utilizado é o que tem pregos dispostos sobre
uma malha quadrada.
A figura 1 ilustra um geoplano de madeira com 9 pinos, também de madeira, em cada
lado.
Figura 1 – Geoplano
Os pinos são utilizados para colocar elásticos que formarão figuras para serem utilizadas
nas atividades. Uma outra opção para a construção do geoplano é utilizar isopor e palitos de
madeira ou alfinetes, que farão o papel do prego.
Figuras com simetria
I Simpósio Nacional de Ensino de Ciência e Tecnologia – 2009
Página: 1113
ISBN: 978-85-7014-048-7
Universidade Tecnológica Federal do Paraná - UTFPR
Programa de Pós-Graduação em Ensino de Ciência e Tecnologia - PPGECT
A atividade de construção de figuras simétricas sempre é abordada em artigos com o uso
do Geoplano. A Construção dessas figuras é bem diversificada, só depende da criatividade de cada
aluno. A figura 2 mostra três construções feitas no Geoplano com simetria de rotação e reflexões
na horizontal, vertical e diagonal.
Figura 2 – Aplicação de simetria de rotação e reflexões.
Na figura 3, tem-se uma figura construída sobre o geoplano com elásticos de cores branca
e rosa na qual foi utilizado apenas simetria de rotação. Observe que, dividindo a figura em 4
quadrantes, a única maneira de obter a figura do outro quadrante é aplicando rotação de 90
graus.
Figura 3 – Simetria de Rotação.
Em (Bressan, 2006a), as simetrias de rotação, translação e reflexão são exemplificadas
com diversas figuras.
Para complementar o assunto, pode-se utilizar o software Kali. Ele tem uma opção para a
construção de rosáceas com motivos retilíneos e curvilíneos. De fácil manuseio, pode ser obtido
gratuitamente na Internet.
I Simpósio Nacional de Ensino de Ciência e Tecnologia – 2009
Página: 1114
ISBN: 978-85-7014-048-7
Universidade Tecnológica Federal do Paraná - UTFPR
Programa de Pós-Graduação em Ensino de Ciência e Tecnologia - PPGECT
Padrões de Simetria em faixas
A simetria utilizada na construção de faixas faz uso da translação, reflexão, rotação e
translação refletida. Com essas transformações é possível construir qualquer um dos sete tipos de
faixa como mostra (Bressan, 2006a).
Na figura 4, tem-se uma faixa construída no Geoplano. Como foram utilizadas duas linhas
do Geoplano com oito quadrados, pode-se chamá-la de faixa de ordem 2x8(dois por oito).
Figura 4 – Faixa com simetrias de rotação, reflexão e translação.
Analisando a figura 4, nota-se o uso de translação, reflexão na horizontal, reflexão na
vertical e rotação. Assim, essa faixa é classificada no padrão 6 como mostra (Bressan, 2006a).
Um resumo dos padrões de faixa apresentada pela autora nesse artigo pode ser visto na
tabela 1:
Tabela 1 –Padrões de simetria para faixas.
Padrões
Translação
Reflexão
Horizontal
Reflexão
Vertical
Rotação
Translação
Refletida
I
II
III
IV
V
VI
VII
O padrão 6 é o que possui todas as simetrias, incluindo a de translação refletida que
ocorre em conjunto com a reflexão na horizontal.
A faixa apresentada na figura 5 possui simetria de translação e reflexão na horizontal.
Analisando a tabela 1, percebe-se que não existe um padrão apenas com essas duas
transformações, mas também aparece a translação refletida. Assim, conclui-se que sempre que
I Simpósio Nacional de Ensino de Ciência e Tecnologia – 2009
Página: 1115
ISBN: 978-85-7014-048-7
Universidade Tecnológica Federal do Paraná - UTFPR
Programa de Pós-Graduação em Ensino de Ciência e Tecnologia - PPGECT
ocorrer reflexão na horizontal também ocorre a translação refletida, em que a recíproca não é
verdadeira, pois o padrão 3 possui a translação refletida e não possui a reflexão horizontal.
Figura 5 – Faixa com reflexão na horizontal.
O padrão 2, que possui translação e reflexão na vertical, pode ser observado na faixa da
figura 6. Essa faixa possui ordem 3x8(três por oito) e foi elaborada com 18 elásticos.
Figura 6 – Faixa com reflexão na horizontal.
Pavimentação de um plano com o Geoplano
Os padrões para pavimentar um plano podem ser obtidos aplicando transformações
geométricas que vão desde rotações de 60, 90, 120 e 180 graus até reflexões na horizontal,
vertical e diagonal à direita e esquerda, além de translação na horizontal e vertical. O padrão
mostrado na figura 7 foi obtido utilizando apenas translação horizontal e vertical.
I Simpósio Nacional de Ensino de Ciência e Tecnologia – 2009
Página: 1116
ISBN: 978-85-7014-048-7
Universidade Tecnológica Federal do Paraná - UTFPR
Programa de Pós-Graduação em Ensino de Ciência e Tecnologia - PPGECT
Figura 7 – Padrão com translação horizontal e vertical.
Aplicando as simetrias de rotação citadas anteriormente na figura 7, obtêm-se os padrões
mostrados na figura 8.
Figura 8 – Padrões com rotação de 60, 90,120 e 180º.
A construção desses padrões foi possível com o auxílio do software Tess, específico para a
construção de rosáceas ou rosetas, faixas ou frisos e mosaicos. Uma versão de demonstração
pode ser obtida gratuitamente na internet. Em (Bressan, 2006b) é possível saber mais sobre o
software.
O estudo matemático desses padrões para pavimentar o plano é feito por (LedergerberRuoff, 1982) e comentado historicamente em (Barbosa, 1993).
Com o geoplano, é possível construir algumas pavimentações observando apenas as
principais simetrias que, quando combinadas entre si, geram 17 padrões diferentes para
pavimentar um plano.
Na figura 9, tem-se uma pavimentação construída no geoplano com o uso de elásticos. As
principais simetrias existentes são translações na horizontal e vertical, rotação de 90 graus e
simetria de reflexão na horizontal, vertical e diagonal.
I Simpósio Nacional de Ensino de Ciência e Tecnologia – 2009
Página: 1117
ISBN: 978-85-7014-048-7
Universidade Tecnológica Federal do Paraná - UTFPR
Programa de Pós-Graduação em Ensino de Ciência e Tecnologia - PPGECT
Figura 9 – Pavimentação
Como o geoplano é formado por quadrados, eles podem aparecer em diversas
pavimentações como mostra a figura 10. Nos dois casos foram utilizados dois planos de cores
diferentes. No primeiro caso, colocaram-se os elásticos verdes e depois os de cor branca. Para o
segundo caso, foi feita a base com elásticos brancos e depois com elásticos de cor rosa, dando a
idéia de unir os quadrados brancos.
Figura 10 – Pavimentação
A simetria de translação na horizontal e vertical ocorre em todas as pavimentações, caso
contrário não seria possível preencher uma região plana. Essa simetria pode ser observada na
figura 11, em que o padrão em formato de X é repetido na horizontal e na vertical como mostra o
esquema ao lado da figura.
I Simpósio Nacional de Ensino de Ciência e Tecnologia – 2009
Página: 1118
ISBN: 978-85-7014-048-7
Universidade Tecnológica Federal do Paraná - UTFPR
Programa de Pós-Graduação em Ensino de Ciência e Tecnologia - PPGECT
Figura 11 – Pavimentação
Com o uso do Geoplano, podem-se encontrar diferentes pavimentações com motivos
retilíneos diversos. A figura 12 mostra duas pavimentações, em que a primeira serviu de base
para a construção da segunda pavimentação. Os elásticos de cor rosa foram colocados sobre os
brancos em sentido contrário.
Figura 11 – Pavimentação
Considerações finais
O conceito de simetria e aplicações na construção de faixas, rosáceas e mosaicos podem
ser trabalhadas com o auxílio de disciplinas de História e Educação Artística. Na Matemática,
como foi mostrado neste artigo, uma ferramenta simples e de fácil uso é o Geoplano que pode
ser construído com madeira e pregos ou isopor e alfinetes.
I Simpósio Nacional de Ensino de Ciência e Tecnologia – 2009
Página: 1119
ISBN: 978-85-7014-048-7
Universidade Tecnológica Federal do Paraná - UTFPR
Programa de Pós-Graduação em Ensino de Ciência e Tecnologia - PPGECT
O seu uso permite que alunos criem e recriem, formulando conceitos e desenvolvendo a
criatividade de uma maneira simples e divertida, juntamente com o auxílio dos colegas e do
professor.
Para os professores que gostam de inovar e prender a atenção dos discentes, propor
atividades variadas com o Geoplano pode ser uma solução para as aulas que, muitas vezes, não
são consideradas interessantes.
Referências
Barbosa, R. M. Descobrindo padrões em Mosaicos. São Paulo: Atual. 1993.
Bressan, R. Construindo Faixas simétricas. In: III Seminário Internacional de Pesquisa em
Educação Matemática, Águas de Lindóia, 2006.
_________. Ferramentas para o ensino de Matemática. Mosaico - Revista de Pesquisa da área de
Ciências Exatas da UNIFEV, Votuporanga, v. 1, n. 2, 2006.
Lederberger-Ruoff, E. B. Isometrias e ornamentos no plano Euclidiano. São Paulo: Atual. 1982.
Rosemeire Bressan: professora da Faculdade de Tecnologia de Catanduva(FATEC) e Centro
Universitário de Votuporanga(UNIFEV). [email protected]
I Simpósio Nacional de Ensino de Ciência e Tecnologia – 2009
Página: 1120
ISBN: 978-85-7014-048-7