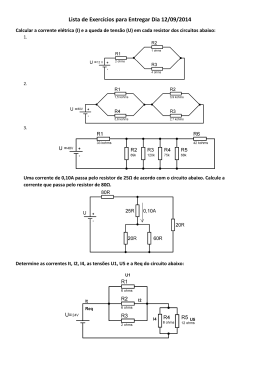
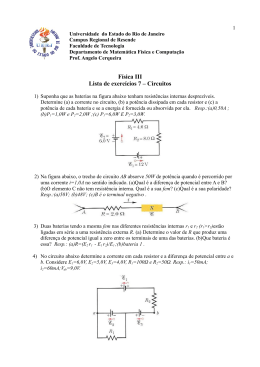
F328 – Física Teórica III
UNICAMP – IFGW
[email protected]
Circuitos
Calculando a corrente em circuito de malha única
A equação de potência ( P = Ri2 ) estabelece que, em um intervalo de
tempo dt, a energia Ri2dt aparecerá na resistência ( resistor ) do circuito,
como energia térmica. Durante este mesmo intervalo de tempo, uma carga
dq = idt terá se movido através da bateria B, e o trabalho que a bateria
realizou sobre esta carga terá sido:
dW
Do princípio de conservação da energia temos:
leva a
R i , ou
a) Através da energia
i
(volt)
R( )
cuja unidade é o Ampére (A) .
dq
i dt
i dt
R i 2 dt , que nos
Circuitos
Regras práticas para calcular a diferença de potencial
através de um circuito
Sentido a percorrer
Sentido a percorrer
Circuito RC
Calculando a corrente
dq
dt
i
i0
(
t
t
i (t ) C
1
e
RC
é a corrente máxima)
R
0
q(0) 0, i (0)
q( )
R
C , i( ) 0
q (t )
i (t )
C
R
t / RC
R
e
t / RC
i0 e
t / RC
Observe que a corrente tem valor
inicial igual a
e decresce até
R
zero quando capacitor se torna
completamente carregado.
Um capacitor em processo de
carga, inicialmente (t=0) funciona
como um fio de ligação comum em
relação à corrente de carga.
Decorrido um longo tempo
funciona como um fio partido.
Circuito RC
b) Descarregando um capacitor: chave S
na posição b do circuito em t = 0. O
capacitor (inicialmente carregado) vai
descarregar através de R. Como variam
agora q(t) e i(t) no circuito?
A equação diferencial do circuito,
neste caso, fica:
dq
R
dt
Circuito básico para carga e
descarga de um capacitor
q(t )
q0 e
i (t )
dq
dt
Com as soluções
No processo de descarga tanto a
carga como a corrente diminuem
exponencialmente com o tempo.
t
RC
, q0
i0 e
t
t
0
t
q
C
0
C
RC
q0
RC
, i0
q(0)
q0
C , i (0)
i0
q( ) 0, i (0) 0
Longo tempo
Carga do capacitor diminuindo
Exercício - 01
Questão 1. Qual a corrente em termos de e R, indicada pelo
amperímetro A da figura? Suponha que seja nula a
resistência do amperímetro.
Exercício - 02
Questão 3. Uma bateria de 6V, com resistência interna
desprezível, é utilizada para carregar um capacitor de 2 F
através de um resistor de 100 . Determine:
(a) A corrente inicial
(b) A carga final no capacitor
(c) O tempo necessário para a carga atingir 90% do seu valor
final
(d) A carga quando o valor da corrente for igual à metade do
seu valor inicial
Exercício -03
Questão 4. No circuito que aparece abaixo o capacitor está inicialmente
descarregado com a chave aberta. Em t=0 a chave é fechada.
(a) Qual a corrente fornecida pela fem logo depois de a chave ser fechada?
(b) Deduza a expressão da corrente que passa pela fem em qualquer instante
em que a chave está fechada.
(c) Depois de um longo intervalo de tempo, a chave é aberta. Quanto tempo se
passa para que a carga no capacitor diminua de 10% de seu valor quando
a chave foi aberta, se R1=R2=5 e C = 1,0 F?
(d) Qual a corrente muito tempo depois da chave ser ligada?
Exercício - 04
Questão 2. Um resistor de 11 é ligado aos terminais de uma
bateria com fem de 6V e resistência interna de 1 .
Determine:
(a) A corrente
(b) A tensão útil da bateria
(c) A potência fornecida pela fonte da fem
(d) A potência fornecida ao resistor externo
(e) A potência dissipada pela resistência interna da bateria
(f) Se a bateria for de 150 A.h., qual será a energia nela
armazenada?
Exercício -05
Questão 5. Um capacitor, inicialmente descarregado, foi totalmente carregado
por um dispositivo de fem constante ligado em série com um resistor R.
(a) Mostre que a energia final armazenada no capacitor é metade da energia
fornecida pela bateria.
(b) Por integração direta de Ri2 no tempo de carregamento, mostre que a
energia térmica dissipada pelo resistor é também metade da energia
fornecida pela fem.
Bom estudo!!!