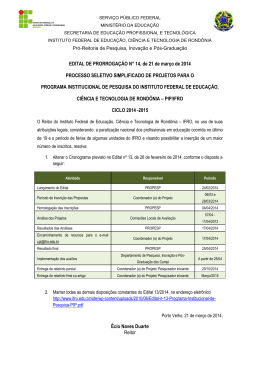
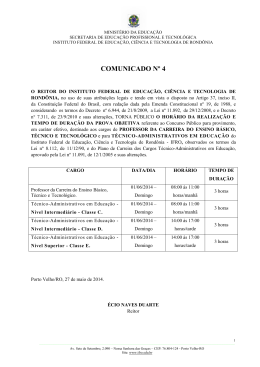
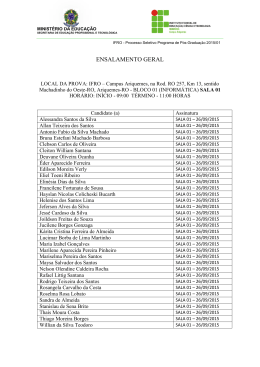
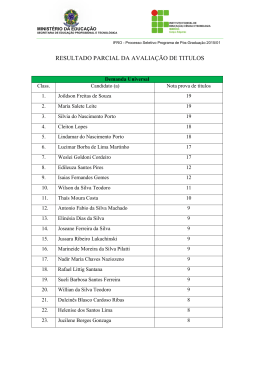
A.3.2 - Ensino de Física.
Instrumentos Matemáticos para Aplicação da Física Moderna no Ensino Médio.
1
2
3
Clever Reis Stein , Moacy José Stoffes Junior , Paulo Renda Anderson , Paulo Roberto dos Santos
4
1. Professor de Física do Instituto Federal de Rondônia - IFRO;
2. Professor de Física do Instituto Federal de Rondônia - IFRO;
3. Professor de Física do Instituto Federal de Rondônia - IFRO; *[email protected]
4. Professor de Engenharia eletrônica do Instituto Federal de Rondônia - IFRO.
Palavras Chave: Física Moderna, Ensino de Física, estratégias.
Introdução
Há inúmeras propostas da inclusão dos conteúdos de
Física moderna ao ensino médio, algumas inclusive
contempladas em alguns livros didáticos, entretanto, os
conceitos matemáticos são deficientemente desenvolvidos.
Este trabalho irá expor uma proposta de estratégia didática
para desenvolver conteúdos de Física Moderna no ensino
médio de forma simples, mas sem perder o rigor
matemático. Para isso vamos abordar: A distribuição de
energia em corpos aquecidos, por Max Planck, os
postulados de Born para explicar o modelo atômico de
Rutherford e a hipótese de de Broglie (dualidade PartículaOnda). Abordando os contextos históricos e incorporando
os instrumentos matemáticos que ainda estão acessíveis
ao ensino médio. Trata-se de um relato experiência de
uma aula cuidadosamente elaborada e aplicada.
Resultados e Discussão
Em fins do século XVIII, uma das dificuldades da física
consistia na interpretação das leis que governam a
emissão de radiação por parte dos corpos negros. Para o
entendimento da dificuldade encontrada partiremos da
teoria clássica da radiação de cavidade (corpo negro) com
a lei da equipartição clássica, onde cada onda estacionaria
na cavidade tem uma energia total média.
Sendo a densidade de energia (
T).
quantum. 3) Quando ocorre o salto de um elétron entre
órbitas, a diferença de energia é emitida (ou absorvida) por
um fóton, que tem energia igual exatamente a diferença de
energia entre as órbitasem questão. 4) As órbitas
permitidas depende valores quantizados de momento
angular orbital L de acordo com a equação:
Onde n é o número quântico principal, também estudado
na química. Seu modelo explicou o espectro de radiação
discreto para o átomo de hidrogênio observado
experimentalmente, obtendo a equação de energia:
Para de Broglie, tais restrições ao movimento do elétron
em torno do núcleo, postulado por Borh, expressadas pelo
surgimento dos números quânticos inteiros mostrava-se
extremamente contrárias a natureza continua dos
movimentos da mecânica clássica, portanto seria
necessário uma nova mecânica onde as ideias quânticas
ocupasse um lugar de base. Os resultados conhecidos
diziam que para onda vale:
De Broglie propôs então que a matéria teria um
comprimento de onda associado a ela dado pela
expressão:
-23
Onde k =1,38 x 10 J/K é a constante de Boltzman. A
problemática existia quando λ (comprimento de onda)
tende a zero. Isso implica que a intensidade de energia
eletromagnética absorvida ou emitida (I) tende ao infinito,
violando a lei da conservação de energia. Solução
proposta por Planck foi tomar valores discreto
(quantizados) de energia, assim
-34
Onde h = 6,63x10 J.s é a constante de Planck, definindo
a energia total média por:
e a densidade de energia:
Definindo:
Através das descrições quânticas da radiação
eletromagnética propostas por Albert Einstein (efeito
fotoelétrico) e Max Planck, o físico Niels Bohr desenvolve
seu modelo atômico (Rutherford) a partir de quatro
postulados: 1) Os elétrons que circundam o núcleo
atômico existem em órbitas que têm níveis de energia
quantizados. 2)
Energia total do elétron não pode
apresentar valor algum e sim, valores múltiplos de um
Chamado de dualidade Partícula-Onda. Após a aula,
conforme proposta, aplicou-se uma avaliação na qual se
observou que os alunos conseguiram compreender os
conceitos físicos como também as equações matemáticas
que são igualmente importantes para o entendimento dos
fenômenos.
Conclusões
O assunto se limitou as relações da parte do estudo que
mesclava a Mecânica Clássica com a Mecânica Quântica,
devido a uma fácil compreensão da matemática utilizada
podendo até ser levada ao ensino médio.
Com a
elaboração e aplicação desta aula mostrou-se que é
possível desenvolver efetivamente os conteúdos de Física
Moderna no ensino médio, não ficando restrito a alguns
capítulos no final dos livros didáticos que abordam os
conteúdos mais a titulo de curiosidade. Assim, compete
aos professores se aprofundarem e procurarem maneiras
de inserir de forma simples, mas não simplista.
67ª Reunião Anual da SBPC