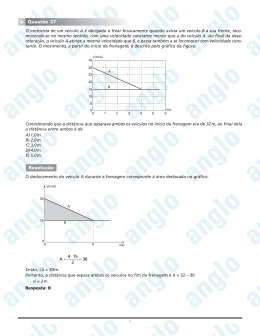
MATEMÁTICA – PROFESSOR (A) PEIXOTO
ALUNO (A): ____________________________________________________________________________
SÉRIE(S): ________ UNIDADE: CENTRO TURMA: ________ DATA: ________/________/2015
Aula 1: Proporção
1. Um quebra-cabeça de 100 peças mede 26 cm por
36 cm, enquanto outro quebra-cabeça de 2.000 peças
mede 48 cm por 136 cm. Nessas condições,
a) calcule a razão entre a área média de uma peça do
quebra-cabeça de 100 peças e do quebra- cabeça
de 2.000 peças, nessa ordem.
b) Se uma pessoa gastou 10 horas para montar o
quebra-cabeça de 100 peças e 360 horas para
montar o quebra-cabeça de 2.000 peças, calcule a
diferença entre a quantidade média de peças que
ela colocou, por hora, para montar cada um dos
quebra-cabeças.
2. O tempo necessário para um veículo parar, em
uma situação de emergência, é, normalmente,
calculado pela soma de dois componentes: o tempo
de reação do condutor e o tempo de frenagem. O
primeiro, considerado constante, é o tempo médio
decorrido desde o momento em que o condutor
percebe o obstáculo até o momento em que os freios
são acionados e entram em funcionamento. O tempo
de frenagem é o tempo que o veículo leva para parar
depois de acionados os freios, e é proporcional à
velocidade
do
veículo
antes
da
frenagem
(desaceleração constante).
Para determinadas condições padrão do veículo e da
via, foi construída uma tabela que informa o tempo
necessário para parar, dependendo da velocidade
pela qual o veículo trafega. Segundo essa tabela, a
uma velocidade de 50 km/h, são necessários 9 s para
parar o veículo, enquanto, a 90 km/h, são necessários
15 s.
De acordo com estes dados, determine qual é o tempo
de reação do condutor considerado e calcule a
distância percorrida pelo veículo, inicialmente com
velocidade constante de 90 km/h, do momento em que
o condutor percebe o obstáculo, até a parada do
veículo.
3. Dois amigos decidem fazer uma caminhada em
uma pista circular, partindo juntos de um mesmo lugar,
percorrendo-a em sentido contrário, caminhando com
velocidades constantes, sendo que a velocidade de
um deles é igual a 80% da velocidade do outro.
Durante a caminhada, eles se encontraram diversas
vezes. Determine qual é o menor número de voltas
que cada um deles deve dar para que eles se
encontrem novamente no ponto de partida.
4. Segundo uma reportagem publicada pelo jornal
Folha de S. Paulo (20/09/2009, p. C1), o Metrô de São
Paulo pretende trocar as escadas rolantes das suas
estações, substituindo as atuais, com velocidades
fixas de 0,5 ou 0,65 m/s, por novos equipamentos com
velocidade de até 0,75 m/s.
A reportagem ainda informa que, em uma escada de
15 m com velocidade de 0,5 m/s, a capacidade de
transporte em uma hora é de 9000 pessoas, em
média.
Uma das maneiras de aumentar a capacidade de
transporte em uma escada é reduzir o tempo do
percurso, aumentando a sua velocidade.
De acordo com estes dados, para que a capacidade
de transporte em uma escada de 15 m seja de 12780
pessoas em uma hora, em média, calcule qual será o
tempo gasto por uma pessoa para subir essa escada.
5. Um paciente deve receber, por via intravenosa,
uma solução de soro glicosado, durante um período T
em horas. Sabendo-se que o volume de 1 mL
corresponde a 20 gotas de soro,
a) qual frequência em gotas por minuto deve ser
administrada, para que um volume de 900 mL de soro
seja aplicado durante 6 horas?
b) obtenha uma expressão que dê o número de gotas
a serem administradas, por minuto, em função do
volume V de soro, em mL, e do tempo T, em horas.
6. Para encher um recipiente de 5 litros, uma torneira
gasta 12 segundos. Uma segunda torneira gasta 18
segundos para encher o mesmo recipiente. Nestas
condições, para encher um tanque de 1000 litros,
usando as duas torneiras ao mesmo tempo, serão
necessários
a) 20 minutos.
b) 24 minutos.
c) 33 minutos.
d) 50 minutos.
e) 83 minutos.
7.
Em uma pesquisa sobre o analfabetismo em
matemática, foram entrevistadas 2000 pessoas,
amostra que representa 110 milhões de brasileiros
entre 15 e 64 anos de idade. Dentre os entrevistados,
60 foram considerados analfabetos absolutos em
matemática.
(Disponível
em:
http://www.ipm.org.br/na_ind_inal_2.php, adaptado)
Com base nas informações do texto, calcule o número
estimado de brasileiros entre 15 e 64 anos,
analfabetos absolutos em matemática.
8. Uma certa marca de cereal em barra disponibiliza
seu produto nas versões normal e light, em caixas
com três barras de 25 g cada uma. Segundo a
informação nutricional do produto, cada 100 g da
versão normal tem 100 calorias e cada 100 g da
versão light tem 80 calorias. Qual é a diferença
calórica entre uma barra normal e uma light?
Página 1 de 6
MATEMÁTICA – PROFESSOR (A) PEIXOTO
ALUNO (A): ____________________________________________________________________________
SÉRIE(S): ________ UNIDADE: CENTRO TURMA: ________ DATA: ________/________/2015
9. Hoje, são fabricados veículos, denominados flex,
que podem ser abastecidos com gasolina e/ou com
álcool. O preço de um modelo flex é R$ 24.464,00 e o
preço do mesmo veículo convencional é R$
22.000,00. Considere que o consumo usando apenas
álcool, no modelo flex, seja 30% maior que o consumo
de gasolina no veículo convencional ou flex, e que o
preço do litro de álcool seja 50% menor que o preço
do litro de gasolina. Quantos dias, no mínimo, serão
necessários para que um taxista recupere o valor
pago a mais no modelo flex, usando apenas álcool, se
ele gasta 40 litros de gasolina todo dia com preço de
R$ 2,00 o litro?
a) 65
b) 77
c) 88
d) 90
e) 115
grandezas x, y e y, z são ambos inversamente
proporcionais, então x e z são grandezas diretamente
proporcionais.
(
) (
) Se y = f(x), com x e y sendo grandezas
diretamente proporcionais, e w = g(z), com z e w
sendo grandezas inversamente proporcionais, então o
quociente y/w e o produto xz formam um par de
grandezas diretamente proporcionais.
(
) ( ) Se x1, y1 e x2, y 2 são pares de grandezas
diretamente proporcionais, com a mesma constante
de proporcionalidade, então x2 y1 = x1 y2.
( ) ( ) A área a e o lado ℓ de um hexágono regular
(a = f(ℓ), para todo ℓ > 0) são grandezas diretamente
proporcionais.
10.
Uma confeiteira deseja comprar 2,6 kg de
achocolatado em um supermercado, que é vendido
em embalagens de 200 g, 400 g e 1 kg, a R$1,80,
R$2,80 e R$6,80, respectivamente. Quantas unidades
de cada tipo de embalagem ela deve comprar, para
gastar o menor valor possível?
14.
Em uma amostra retirada de um tanque de
combustível, verifica-se que 1/7 é de álcool e o
restante é de gasolina pura. Sabendo-se que o total
que havia no tanque era 2800 litros, determine a
quantidade de cada uma das substâncias, álcool e
gasolina pura, presentes no combustível.
11. Em uma maratona de 42 km, o ponto de saída
coincide com o de chegada. Os organizadores da
prova definiram que seriam montados pontos de apoio
para que um maratonista, que corre 5 m/s em média,
encontrasse um desses pontos a cada 10 minutos.
a) Quantos pontos de apoio serão montados se na
saída/chegada é montado um?
b) Qual a distância, em metros, entre dois desses
pontos consecutivos?
15. Analise o desenho.
12.
Um tonel contém 72 litros de uma mistura
homogênea de água e vinho, na proporção de 20% de
água e 80% de vinho. Após retirar-se um balde cheio
dessa mistura e, em seguida, completar-se o volume
inicial do tonel com água pura, constatou-se que a
quantidade de água existente no tonel é de 19,6 litros.
Qual é a capacidade do balde?
Tendo em vista que, na planta acima, a quadra A
13. Diz-se que duas grandezas positivas, x e y, são
diretamente proporcionais, quando existe uma função
linear f(x) = kx, com k > 0, chamada constante de
proporcionalidade, tal que y = f(x), para todo x > 0. De
modo análogo, diz-se que x e y são inversamente
proporcionais, quando existe uma função g(x) = c/x,
com c > 0, tal que y = g(x), para todo x > 0.
De acordo com essas definições, julgue os itens a
seguir.
(
) (
) Se y = g1(x) e z = g2(y) e os pares de
possui uma área de 1800 m2 , a escala numérica da
planta é:
a) 1:10000
b) 1:1000
c) 1:100
d) 1:10
16. Uma pequena empresa foi aberta em sociedade
por duas pessoas. O capital inicial aplicado por elas foi
de 30 mil reais. Os sócios combinaram que os lucros
Página 2 de 6
MATEMÁTICA – PROFESSOR (A) PEIXOTO
ALUNO (A): ____________________________________________________________________________
SÉRIE(S): ________ UNIDADE: CENTRO TURMA: ________ DATA: ________/________/2015
ou prejuízos que eventualmente viessem a ocorrer
seriam divididos em partes proporcionais aos capitais
por eles empregados. No momento da apuração dos
resultados, verificaram que a empresa apresentou
lucro de 5 mil reais. A partir dessa constatação, um
dos sócios retirou 14 mil reais, que correspondia à
parte do lucro devida a ele e ainda o total do capital
por ele empregado na abertura da empresa.
Determine o capital que cada sócio empregou na
abertura da empresa.
17. Em uma rodovia, um motorista acionou o freio de
seu carro quando sua velocidade era de 80 km/h,
percorrendo ainda 60 m até parar completamente.
Sabe-se que a distância percorrida por esse veículo
até parar é diretamente proporcional ao quadrado da
sua velocidade. Caso a frenagem tivesse ocorrido
num momento em que a velocidade fosse de 120
km/h, antes de parar o veículo teria percorrido
a) 135 metros.
b) 124 metros.
c) 95 metros.
d) 147 metros.
18. Uma caixa d'água pode ser abastecida por duas
bombas, A e B. Estando a caixa vazia, a bomba A leva
5 horas para enchê-la e a bomba B, 7,5 horas. Certo
dia, às 7 horas da manhã, a caixa estava totalmente
vazia e, naquele momento, a bomba A foi ligada. Após
1,5 horas, ligou-se também a bomba B,
permanecendo as duas ligadas até encher
completamente a caixa. Considerando que no período
em que as bombas estavam ligadas, não houve
nenhuma saída de água da caixa, a que horas as
bombas terminaram de encher totalmente a caixa?
Página 3 de 6
MATEMÁTICA – PROFESSOR (A) PEIXOTO
ALUNO (A): ____________________________________________________________________________
SÉRIE(S): ________ UNIDADE: CENTRO TURMA: ________ DATA: ________/________/2015
espaço percorrido até parar, em movimento retilíneo
uniformemente retardado, é tal que
Gabarito:
Resposta
da
questão
1:
a) A área média de uma peça do quebra-cabeça de
26  36 234
100 peças é

cm2 . A área média de
100
25
uma peça do quebra-cabeça de 2.000 peças é
48  136 408

cm2 .
2000
125
234
195
Portanto, a razão pedida é igual a 25 
.
408
68
125
100
b) A pessoa colocou
 10 peças por hora no
10
2000 50
quebra-cabeça de 100 peças e
peças por

360
9
hora no quebra-cabeça de 2.000 peças. Logo, o
50 40
resultado pedido é 10 

.
9
9
Resposta
da
questão
2:
Sejam fi e r, respectivamente, o tempo de frenagem
correspondente à velocidade vi e o tempo de reação.
De acordo com as informações, temos f1  r  9 e
f2  r  15. Logo, f2  f1  6. Por outro lado, como
fi  k  vi, sendo k a constante de proporcionalidade,
vem
3
k  90  k  50  6  k 
.
20
Assim, encontramos
3
 50  r  9  r  1,5 s.
20
O espaço percorrido pelo veículo durante o tempo de
reação é dado por
02  252  2 
25
25  13,5
 ΔS  ΔS 
13,5
2
 ΔS  168,75 m.
Portanto, a distância percorrida pelo veículo, do
momento em que o condutor percebe o obstáculo, até
a
parada
do
veículo
é
igual
a
37,5  168,75  206,25 m.
Resposta
da
questão
Sejam v1 e v2 as velocidades dos dois amigos.
4
v 2. Se t1 e t 2
5
denotam os tempos que os dois amigos levam para
dar uma volta completa, segue que:
t
4
v1  t1  v 2  t 2  v 2  t1  v 2  t 2  2  .
t1 5
Suponhamos que v1  80%  v 2 
Seja T o tempo que os dois amigos levam para se
encontrar no ponto de partida pela primeira vez. É
T
T
imediato que n1 
e n2  , sendo n1 e n2 o
t1
t2
número inteiro de voltas dadas por cada um dos
n
t
4
amigos. Assim, 1  2   n1  4 e n2  5.
n2 t1 5
Portanto, o mais lento deverá dar 4 voltas, enquanto
que o mais rápido deverá dar 5 voltas.
Resposta
da
questão
4:
Se a capacidade de transporte da escada é
diretamente proporcional à sua velocidade, isto é,
c  k  v,
k
com
sendo
a
constante
de
proporcionalidade, temos: 9000  k  0,5  k  18.000.
c  12.780,
Daí,
para
vem:
12780  18000  v  v  0,71m s.
Portanto, o tempo gasto por uma pessoa para subir
15
 21,13 segundos.
essa escada é dado por:
0,71
90
 1,5  37,5 m.
3,6
Resposta
da
a) 50 gotas por minuto.
Considerando que o veículo se desloca a uma
90
 25m s, seu tempo de
velocidade de 90km h 
3,6
frenagem é igual a 15  1,5  13,5 s. Logo, sua
b) V/(3T) gotas por minuto.
desaceleração é igual a
25
m s2 e, dessa forma, o
13,5
3:
questão
5:
da
questão
6:
Resposta
da
3.300.000 pessoas
questão
7:
Resposta
[B]
Página 4 de 6
MATEMÁTICA – PROFESSOR (A) PEIXOTO
ALUNO (A): ____________________________________________________________________________
SÉRIE(S): ________ UNIDADE: CENTRO TURMA: ________ DATA: ________/________/2015
C1  6L1
Resposta
5 calorias
da
questão
8:
Resposta
[C]
da
questão
9:
C1  L1  14000

L1  2000
C1  12000
Portanto,
L2  5000  2000  3000
C2  30000  12000  18000
.
,
Resposta
da
questão
10:
duas embalagens de 1kg, uma embalagem de 400g e
uma de 200g.
ou seja, os capitais investidos foram R$ 12.000,00 e
Resposta
a) 14
Resposta
[A]
da
questão
11:
b) 3.000 metros
Resposta
6,5 litros
da
questão
12:
Resposta
VVVF
da
questão
13:
Resposta
Álcool: 400ℓ
Gasolina: 2400ℓ
da
questão
14:
Resposta
[B]
da
questão
15:
Área
da
quadra
4
A
na
planta
em
R$ 18.000,00.
da
questão
17:
Resposta
da
10 horas e 36 minutos
questão
18:
2
m:
2
0,06  0,03  18  10 m
Razão entre as áreas:
18  10 4
 10 6
1800
Logo, a escala será dada por:
106  103 
1
.
1000
Resposta
da
questão
16:
Sejam C1 e C2, respectivamente, os capitais
investidos pelos dois sócios.
Logo,
C1  C2  30000.
Além disso, sabemos que os lucros L1 e L2 são
proporcionais aos capitais investidos. Então,
L1 L2
L L
L
L
5000

 1 2  1
 1  C1  6L1.
C1 C2
C1  C2 C1
30000 C1
Como um dos sócios efetuou uma retirada de 14 mil
reais, correspondente ao capital investido mais a parte
que lhe cabia do lucro total, segue que:
Página 5 de 6
MATEMÁTICA – PROFESSOR (A) PEIXOTO
ALUNO (A): ____________________________________________________________________________
SÉRIE(S): ________ UNIDADE: CENTRO TURMA: ________ DATA: ________/________/2015
14 .......... 34321 ....... Não definida.. Matemática
.............. Ufg/2000 .. Analítica
Resumo das questões selecionadas nesta
atividade
15 .......... 120457 ..... Média ............ Matemática
.............. Ueg/2011 . Múltipla escolha
Data de elaboração:
Nome do arquivo:
16 .......... 102207 ..... Média ............ Matemática
.............. Ueg/2010 . Analítica
31/01/2015 às 09:22
Aula 1 Proporção
Legenda:
Q/Prova = número da questão na prova
Q/DB = número da questão no banco de dados do
SuperPro®
Q/prova Q/DB
Fonte
Grau/Dif.
Tipo
17 .......... 83436 ....... Não definida.. Matemática
.............. Ueg/2008 . Múltipla escolha
18 .......... 75963 ....... Não definida.. Matemática
.............. Ueg/2007 . Analítica
Matéria
1 ............ 128765 ..... Baixa ............. Matemática
.............. Ufg/2014 .. Analítica
2 ............ 124076 ..... Média ............ Matemática
.............. Ufg/2013 .. Analítica
3 ............ 103219 ..... Média ............ Matemática
.............. Ufg/2010 .. Analítica
4 ............ 103222 ..... Média ............ Matemática
.............. Ufg/2010 .. Analítica
5 ............ 83458 ....... Não definida .. Matemática
.............. Ufg/2008 .. Analítica
6 ............ 70312 ....... Não definida .. Matemática
.............. Ufg/2007 .. Múltipla escolha
7 ............ 73093 ....... Não definida .. Matemática
.............. Ufg/2007 .. Analítica
8 ............ 64710 ....... Não definida .. Matemática
.............. Ufg/2006 .. Analítica
9 ............ 62525 ....... Não definida .. Matemática
.............. Ufg/2006 .. Múltipla escolha
10 .......... 64714 ....... Não definida .. Matemática
.............. Ufg/2006 .. Analítica
11 .......... 57053 ....... Não definida .. Matemática
.............. Ufg/2005 .. Analítica
12 .......... 40322 ....... Não definida .. Matemática
.............. Ufg/2001 .. Analítica
13 .......... 40310 ....... Não definida .. Matemática
.............. Ufg/2001 .. Verdadeiro/Falso
Página 6 de 6