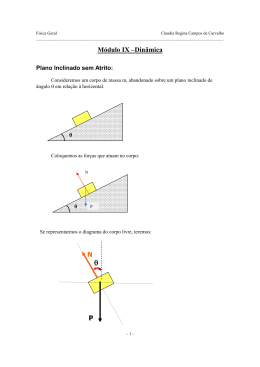
FM.09
1.c
Com a bola solta no ar, na ausência de contato com o jogador, somente a força peso atua sobre a bola.
2.e
P = m · g s P = 100 · 10 = 1.000 N
3.c
I.(V) P = m · g
II. (F) Veja I.
III.(V) A massa independe do local, depende apenas do corpo
(grandeza escalar) e o peso, que é uma força, precisa de módulo, direção e sentido para ser totalmente definido.
4.a
Desprezando-se a resistência do ar, apenas a força peso atua na bola.
5.d
P = m · g s 1 = m · 10 s m = 0,1 kg = 100 g
Uma massa de 100 g é consideravelmente a de uma xicrinha de café
cheia, sendo que um litro de leite tem massa, em média, de 1 kg, e
uma moeda, por volta de 10 g.
6.d
A força resultante na horizontal: Fx = F1 – F3 = 5 – 2 = 3 N. A força
resultante na vertical: Fy = F2 = 4 N. Dessa maneira, a força resultante sobre o corpo será dada por:
FR2 = F x2 + F y2 = 3 2 + 4 2 s FR = 5 N
7.e
Como a aceleração da gravidade local é nula, o peso de cada corpo
também é nulo.
8.e
I.(V) Quanto maior for a massa de um corpo, maior será sua
inércia (dificuldade ao movimento).
II.(V) A força peso é a força que a Terra aplica nos corpos à sua
volta.
III. (V) Peso é uma força e, portanto, vetorial e massa são grandezas
escalar.
9.b
A força normal é uma força de contato e, dessa maneira, é uma força
na qual a mesa exerce sobre o livro que está apoiado sobre ela.
10. d
Se essas forças forem de mesma direção e sentidos opostos:

R = 50 – 30 = 20 N. No entanto, se forem de mesma direção e mes
mo sentido: R = 50 + 30 = 80 N. A força resultante pode variar entre
esses valores, já que as duas forças podem, ainda, diferir em direção.
11. e
As forças que atuam no caixote seriam a força peso (vertical e para
baixo), reação normal do apoio (vertical e para cima) e a força que
o homem empurra o próprio caixote (direção horizontal e sentido
para a direita).
12. a) Na Terra: PT = m · gT = 70 · 10 = 700 N
b) A massa é uma grandeza escalar característica de um corpo.
Portanto, independe da aceleração da gravidade em seu valor:
m = 70 kg
1
c) Na Lua: Plua = m · glua = 70 · 1,6 = 112 N
13. c
Desprezando-se a resistência do ar, a única força atuante na bola é
a força peso.
14.
a
Aplicando a segunda lei de Newton para o sistema em queda:
• para a esfera de baixo: P – T = m · a s 30 – T = 3 · a
• para a esfera de cima: P ’ + T = m’ · a s 10 + T = 1 · a
Resolvendo o sistema de equações: a = 10 m/s2 (como era de se
esperar, pois os corpos estão em queda livre).
Dessa maneira: 10 + T = 1 · a s T = 10 – 10 = 0 N
15.a) Horizontal para a esquerda: sentido oposto à deformação da
mola, que está comprimida, ou seja: deformada para a direita.
b) Movimento uniformemente retardado, já que a mola exerce uma
força contrária à compressão em razão do movimento do trem.
16. c
A componente horizontal da força resultante:
Rx = 10 · cos 37º – 4,0 = 8,0 – 4,0
\ Rx = 4,0 N
A componente vertical da resultante:
RY = 10 · sen 37º – 3,0 = 6,0 – 3,0
\ RY = 3,0 N
Aplicando o Teorema de Pitágoras:
R 2 = R x2 + R y2 = 3 2 + 4 2
\ R = 5,0 N
17. a
A força resultante sobre o carrinho terá direção horizontal e sentido
para a direita (já que não há movimento na vertical), e o seu módulo
será:
R = F1 · cos 30º + F2 · cos 45º = 20 ⋅
3
2
+ 20 ⋅
= 10 ⋅ ( 3 + 2 )
2
2
\ R ∙ 10 · (1,7 + 1,4) = 31 N
18.
N
θ
P

P : força que a Terra faz no corpo (força de campo)
N: força que o plano de apoio faz no corpo (força de contato)
19. b
A massa é uma grandeza escalar, que não depende do local de sua
aferição. Dessa maneira, a massa da mulher, em Júpiter, é a mesma
que na Terra, ou seja, 60 kg.
20. d
T
10º
Ty Ty
P
10º
T
Tarefa Proposta 2
Física
Resolução
Ty = T · sen 10°
No equilíbrio, temos:
P
1.000
=
2Ty = P s 2 · T · sen 10° = P s T =
s
2 · sen 10º 2 · 0, 17
s T = 2.941,2 N
21. b
Para equilibrar o sistema D-C, basta retirar uma moeda do prato
C, já que o limite seriam 3 moedas em cada prato e, assim, ambos
ficariam com duas.
E para equilibrar o sistema B-A, acrescentar ao prato A a moeda
retirada de C, de modo que também ficará cada prato, com duas
moedas. E, assim, o sistema todo se equilibrará.
5.b
• Bloco A: FR(A) = TA – PA s mA · a = TA – mA · g • Bloco B: FR(B) = PB – TB s mB · a = mB · g – TB • Em módulo: TA = TB = T. Assim, em I e II, temos:
(I)
(II)
 2 ⋅ a = T − 20

s
 6 ⋅ a = 60 − T
s 8 ⋅ a = 40 s a = 5 m/s 2 e T = 2 ⋅ 5 + 20 s T = 30 N
O módulo da tração no fio é 30 N.
6.e
22. c
O dinamômetro é graduado de modo a marcar a força aplicada a
um de seus extremos. Dessa maneira, marcará apenas 100N.
A
P
23. e
Determinando, pelo gráfico, as constantes elásticas para cada
mola:
6
Mola A: F = kA · x s k A =
= 200 N/m
0, 03
4
= 80 N/m
Mola B: F = kB · x s k B =
0, 05
Aplicando a força de 8 N em cada uma:
8
= 0, 04 m = 4 cm
200
8
= 0, 1 m = 10 cm
Mola B: F = kB · xB s x B =
80
Mola A: F = kA · xA s x A =
\ xA + xB = 14 cm
24. A força resultante horizontal é devida à componente horizontal da
força F:
FR = Fx = F ∙ cos a = 50 · 0,8
\ FR = 40 N
FM.10
1.d
De acordo com a terceira lei de Newton, trata-se de um par de forças
de ação e reação, ou seja, forças de módulos e direções iguais, mas
sentidos opostos.
Sendo assim, FA = FB.
2.e
FR = N – P s N = FR + P s N = m · a + m · g s N = m (a + g) s
s N = 5,0 · 102 ⋅ (2 + 10) s N = 6,0 · 103 N
3.e
Elevador subindo acelerado:
FR = N – P s m · a = N – m · g s
s N = m ⋅ (a + g) s N = 70 ⋅ (0,5 + 10) s N = 735 N
4.e
•
•
2
Módulo da desaceleração:
v 2= v 02 + 2 · a · ∆s s 0 = (4)2 + 2 · a · 8 s
s a = –1 m/s2 s |a| = 1 m/s2
Tração no cabo durante a desaceleração:
FR = T – P s m · a = T – m · g s
s T = m ⋅ (a + g) s T = 800(1 + 10) s T = 8.800 N = 8,8 · 103 N
28 m
S
B
vA(p) = 2 m/s
a = 2,5 m/s2
No sistema, temos:
PA – PB = (mA + mB) · a s
s mA · g – mB · g = (mA + mB) · a s
s 10 · 10 – mB · 10 = (10 + mB) · 2,5 s
75
= 6 kg
12,5
Pela equação de Torricelli, temos:
v s2 = v P2 + 2a ⋅ ∆s s
s 75 = 12,5 mB s mB =
s v s2 = (2) 2 + 2 ⋅ (2,5) ⋅ (28) s
s v s = 144 = 12 m/s
7.Analisando o resultado em cada bloco, admitindo o sentido de B descendo, temos:
(I)
• T = FA = mA · a
• PB − T = mB · a(II)
De (I) + (II), vem:
m · g – FA
PB − FA = (mA + mB) · a s a =
2m
8.e
• Bloco A: FR(A) = TA – PA s mA · a = TA – mA · g (I)
• Bloco B: FR(B) = PB – TB s mB · a = mB · g – TB (II)
• Dinamômetro: tração T
• Em módulo: T = TA = TB. Assim, em I e II, temos:
 3 ⋅ a = T − 30

s
5 ⋅ a = 50 − T
s 8 ⋅ a = 20 s a = 2,5 m/s 2 e T = 3 ⋅ 2,5 + 30 s T = 37,5 N
Portanto, o dinamômetro indica 37,5 N.
9.c
No gráfico, para x = 15 cm, temos P = 10 N.
Então:
5 bolinhas _____ 10 N
10
s x=2N
x =
1 bolinha _____ x 
5
Portanto, a massa de cada bolinha é:
Tarefa Proposta 2
Física
Resolução
m =
P
2
=
s m = 0,2 kg = 200 g
g 10
FR
m ⋅ a s a = g · tg 14º s
=
m ⋅g
P
s a = 10 · 0,25 s a = 2,5 m/s2
tg 14º =
De acordo com o texto: 200 g custam R$ 2,00.
13. a
Como F = (m1 + m2) · a, temos: 6 = (1 + 2) · a s a = 2 m/s2
No 1º bloco, temos:
T = m1 · a s T = 1 · 2 s T = 2 N
10. a
T
30°
FR
5 − 55 −50
= –25 m/s2 s |a| = 25 m/s2
=
2
2
b)FR = m · a s
s T – P = m · a s T – mg = m · a s T = m · g + m · a
s T = 800 + 80 · 25 = 2.800 N
14.a) a =
P
FR m ⋅ a
=
s a = g · tg 30º s
m⋅ g
P
1
sen 30°
s
sa=g·
s a = 10 ⋅ 2
cos 30°
3
2
10
sa=
m/s2
3
tg 30º =
15. e
Com o sistema em equilíbrio, temos:
P1 + Felás. = T 
 Felás. = m · g
P2 = Felás.

Após cortar o fio:
FR = P2 – Felás. s m · a2 = m · g – m · g s a2 = 0
11. V – F – V – V – F
2
FR = P1 + Felás. s m · a1 = m · g + m · g s a1 = 2 g
1
16.a)
T1
N
Fio 1
A
T
m1
PA
T1
2m
P1
B
T2
PB
T
Fio 2
m2
mA = 3 kg
mB = 2 kg
Para A:
T1 = PA s T1 = mA · g s T1 = 3 · 10 = 30 N
Para B:
PB + T2 = T1 s mB · g + T2 = T1 s
s 2 · 10 + T2 = 30 s T2 = 10 N
Cortando-se o fio 2, temos:
A) PA − T
= mA ⋅ a
1
B ) T 1 − PB = m B ⋅ a
De A + B, temos:
30 − 20 = 5 ⋅ a s a = 2 m/s 2
Assim, em B:
T1 – 20 = 2 · 2 s
s T1 = 24 N
Para o corpo A chegar ao chão, temos:
h = v 0 · t +
12.a) e
a · t2
2⋅t2
s 2=
s t= 2s
2
2
b)
w Sentido do movimento
T
14°
P2
O sistema é acelerado com aceleração de:
∆v
(gráfico)
a=
∆t
1− 0
= 0,5 m/s2
∴ a=
2−0
No corpo de massa m2, temos:
P2 – T = m2 · a s m2 · g – T = m2 · a s
s m2 · 10 – T = 0,5 · m2 (I)
No corpo de massa m1, temos:
T = m1 · a s T = 1 · 0,5 s T = 0,5 N (II)
Substituindo (II) em (I), temos:
0,5
1
kg
=
9,5 19
b) De acordo com a terceira lei de Newton, a força que a bancada
exerce sobre o corpo é uma força igual à tração no fio T = 0,5 N
10m2 – 0,5 = 0,5m2 s 9,5m2 = 0,5 s m2 =
17. c
I.(V)
II.(V)
III.(F) O tempo de queda não depende da massa.
IV.(V)
18. a)
T
P
c)
T
14°
FR
P
3
P
Tarefa Proposta 2
Física
Resolução
b) T – P = m · a s
s T – 500 · 10 = 500 · 2 s
s T = 6.000 N
y
N
m
x
19. Soma = 24 (08 + 16)
(01) (F) Observadores inerciais.
(02)(F) A moeda possui a mesma velocidade do ônibus.
(04) (F) São iguais: ação e reação.
(08) (V) Primeira lei de Newton.
(16) (V) Na descida, velocidade constante implica ∑ F = 0 (equilíbrio estático ou dinâmico).
P
θ
b) A resultante é dada pela projeção da força peso na direção do
deslocamento:
Px = FR = P · sen θ s
s FR = m · g · sen θ (paralela à direção do deslocamento)
Direção: paralela à rampa.
Sentido: contrário ao movimento.
20.
FM.11
T
1.c
As forças que agem no engradado estão mostradas na figura.
T
T
2T
2T
N
Fa
B
PB
4T
A
PA
Como se trata de uma situação de equilíbrio, temos:
PA = 4T s 340 = 4T = 85 N
∴ PB = T = 85 N
21. Soma = 23 (01 + 02 + 04 + 16)
(01) (V) Definição de velocidade média.
(02) (V) Definição de aceleração média.
(04)(V) a =
F
. Como F varia linearmente com o tempo, a também
m
varia linearmente com o tempo.
(08)(F) M =
F
a
(16) (V) Veja resposta 04.
Sentido do movimento
do caminhão
P
• Em módulo: N = P. Portanto:
FR = Fat.
Ou seja, a força de atrito é a resultante das forças externas.
2.a
Como a caixa não desliza sobre a carroceria, ela possui a mesma
aceleração do caminhão:
v = v0 + a · t s 25 = 15 + a · 10 s a = 1,0 m/s2
Na caixa, a força de atrito é a força resultante. Assim:
Fa = m · a s Fa = 1.000 · 1 s Fa = 1.000 N
Sendo 1 kgf = 10 N (aproximadamente), temos: Fa = 100 kgf
3.b
Na velocidade máxima, temos:
Far = P = m · g s Far = 75 · 10 s Far = 750 N
4.d
Atividades extras
22. c
Em módulo:
FBA = FAB = FRB s
s FBA = mB · a s
s FBA = 4 · 2 = 8 N
Analisando o movimento do conjunto, temos:
v2 = v 02 + 2 · a · Ds s
s v2 = 0 + 2 · 2 · 16 s
s v = 64 s v = 8 m/s
23. Soma = 30 (02 + 04 + 08 + 16)
(01)(F) O peso aparente é maior que o peso real.
(02)(V) N = P + FR s N = m ⋅ g + m ⋅ a = m ⋅ (g + a) s
s N = 60 ⋅ (10 + 2) s N = 720 N
(04)(V) N = P – FR s N = m ⋅ g – m ⋅ a = m ⋅ (g – a) s
s N = 60 ⋅ (10 – 1) s N = 540 N
(08) (V) Se FR = 0 s N = P
(16)(V)


24.a) P : força de campo (gravitacional) e N : força de contato (eletromagnética)
4
T
T
B
N
37°
PB
A
Fat
PA
Para que ocorra equilíbrio, temos para o corpo A:
T · cos 37° = Fat. (em que T = PB)
∴ mB · g · cos 37° = μ · N (I)
Na vertical, temos:
PA = N + T · sen 37° s N = mA · g – T · sen 37° (II)
Substituindo II e I:
m B ⋅ g ⋅ cos 37° = μ ⋅ (m A ⋅ g − m B ⋅ g ⋅ sen 37°) s
s mB · 0,8 = 0,5 ⋅ (11 – mB · 0,6) s
s 1,1 · mB = 5,5 s mB = 5 kg
Tarefa Proposta 2
Física
Resolução
5.d
T2
m2
T1
P2 · sen θ
m1
θ
P1
Como os blocos estão em equilíbrio estático:
P1 = P2 · sen θ s
s m1 · g = m2 · g · sen θ
Como m2 = 2m1, temos:
m1 = 2m1 · sen θ s
1
s θ = 30°
2


Como as forças T 1 e T 2 são de tração no mesmo fio, têm módulos
iguais:
T1 = T2
9.Soma = 57 (01 + 08 + 16 + 32)
mA = 600 kg
mB = 1.000 kg
μe = 0,8
μd = 0,5
v0 = 90 km/h = 25 m/s
vf = 0
Ds = 62,5 m
(01) (V) De acordo com a equação de Torricelli.
v2 = v 02 + 2a · Ds
(02)
(04)
FBA
s sen θ =
6.b
Na iminência do movimento, temos:
F · cos 20° = fat s 100 · 0,94 = μ · N (I) (horizontal)
N + F · sen 20° = P s N = 316 – 100 · 0,34 (vertical)
N = 282 N e substituindo em (I), temos:
94 = μ · 282 s μ = 0,33
7.d
a)(F) A resistência do ar é variável.
b)(F) A velocidade aumentaria até a pessoa atingir o solo.
c)(F) A variação de velocidade não é uniforme.
d)(V) ∆st > Área do trapézio + área do retângulo
∴ ∆st >
43 + 23
· 50 + 27 · 10 s ∆st > 2.020 m
2
e) (F) Movimentos: acelerado, uniforme, retardado e uniforme.
PT
PN
20°
P · sen 20° = f at s m · g · sen 20° = μ · m · g · cos 20° s
s μ =
b)
sen 20° 0, 34
s
=
cos 20° 0, 94
s μ = 0,36
Na horizontal, temos: FR = fat s m · a = μ · m · g s
s a = 0,36 · 10 = 3,6 m/s2
Assim, pela equação de Torricelli, temos:
v2 = v 02 – 2a · Ds s Ds =
s
5
∆s =
fat.A
v 02
s
2a
9
s ∆s = 1, 25 m
7, 2
B
fat.B
As forças de atrito estático, em A e B, são dadas por:
fat.A = μe · NA s fat.A = 0,8 · 6.000 = 4.800 N
fat.A = μe · NB s fat.B = 0,8 · 10.000 = 8.000 N
Para o sistema, a resultante de forças fornece:
fat.A + fat.B = (mA + mB) · a
Assim: 12.800 = 1.600 · a s a = 8 m/s2
Portanto, a força de atrito estático, tanto para A quanto B, não
pode ser vencida, uma vez que a desaceleração do caminhão
é de 5 m/s2.
(08) (V) Se A não escorrega, não exerce força alguma em B.
(16) (V) Veja item 04.
(32) (V) De acordo com o desenvolvimento do item, a aceleração
deve ser maior que 8 m/s2 para que as forças de atrito estático
sejam vencidas.
(64)(F) A caixa A não escorrega em função da força de atrito estático
elevada.
10. a) Para o sistema, temos:
F = (m1 + m2) · a s a =
2
= 0,4 m/s2
( 2 + 3)
b) Para o corpo de massa 2 kg, a resultante é a força de atrito.
Assim:
FR = fat. s FR = m1 · a s FR = 2 · 0,4 = 0,8 N
N
fat
FAB
A
8.m = 10 kg
v = 3 m/s (constante)
a) Na rampa, temos:
0 = (25)2 + 2 · a · 62,5 s
s a = –5 m/s2
(F) Existe atrito entre as caixas e a carroceria do caminhão.
(F) Analisando as forças que atuam nos blocos, temos:
11. d
• Força de atrito entre o bloco B e a superfície horizontal:
Fat. = μc ⋅ (mA + mB) · g = 0,2 · (1 + 4) · 10 s Fat. = 10 N
• No bloco A, temos:
FR = m · aA s 24 = 1 · aA s aA = 24 m/s2
• No bloco B:
FR = FB – Fa s mB · aB = FB – Fa s
s 4 · aB = 12 – 10 s aB = 0,5 m/s2
Portanto:
aA – aB = 24 – 0,5 s aA – aB = 23,5 m/s2
12. a
Se inicialmente o bloco está em repouso: F1 = fat. s fat. = 10 N
Como a força F2 < F1 será aplicada ao bloco, contrária à F1, a resultante permanecerá nula, promovendo apenas uma diminuição do
efeito da força de atrito.
Tarefa Proposta 2
Física
Resolução
13. a
De 0,0 s a 5,0 s o movimento é acelerado.
De 5,0 s a 10 s o movimento é retardado.
19. e
F
F
F
=
=
m A + m B 3m + m 4m
• Nas duas experiências: a =
• Na 1a experiência:
14. a
NB
Felás.
B
FB
f1 = mB · a s f1 = m ·
NA
Felás.
FA
PB
F
A
• Na 2a experiência:
f2 = mA · a s f2 = 3m ·
PA
Em A: FR = F – Felás. – FA s mA · a = F – Felás. – FA (I)
Em B: FR = Felás. – FB s mB · a = Felás. – FB De (I) + (II), vem: a ⋅ (mA + mB) = F – FA – FB
Sendo FA = μ · mA · g e FB = μ · mB · g, temos:
a ⋅ (mA + mB) = F – μ · g ⋅ (mA + mB) s
s a =
Portanto, em (II): 4 · 2 = Felás. – 0,4 · 4 · 10 s Felás. = 24 N
24
s x = 0,03 m = 3 cm
800
15. F – V – V – V – F
I.(F) Fat. = μ · N = 0,3 · 4 · 10 s Fat. = 12 N
FR = F – Fat. = 20 – 12 s FR = 8 N
II.(V)
III.(V) FR = m · a s 8 = 4 · a s a = 2 m/s2
IV.(V) v 2 = v 02 + 2 · a · ∆s s v 2 = (1) 2 + 2 · 2 · 12 s
s v = 7 m/s
V.(F) FR = Fat. s 4 · a = 12 s a = 3 m/s2
v2 = v 02 + 2 · a · ∆s s 0 = (7)2 + 2 ⋅ (– 3) · ∆s s ∆s = 8,2 m
16. c
FR = Fat. s m · a = μ · m · g s a = μ · g s a = 0,8 · 10 s a = 8 m/s2
• v2 = v 02 + 2 · a · ∆s s 0 = (20)2 + 2 · (–8) · ∆s s ∆s = 25 m
17.a)
fat.
F
3F
s f2 =
4m
4
Portanto:
(II)
60 − 0, 4 ⋅ 10 ⋅ ( 6 + 4 )
s a = 2,0 m/s2
6+4
Felás. = k · x s 24 = 800 · x s x =
F
F
s f1 =
4m
4
F
f1
= 4
3F
f2
4
s
f1 1
=
f2 3
20. c
Equilíbrio: Fe = Fat. s k · x = μ · N s
s 20 · x = 0,4 · 30 s x = 0,6 m
Como a mola possui um comprimento natural de 20 cm, temos:
d = x + x0 s d = 60 + 20 s d = 80 cm
21. c
Analisando as forças aplicadas à caixa, temos:
N
Fat.
Px
18°
18°
P
Py
Como v é constante, temos:
Px = Fa s P · sen α = μ · N s
s P · sen α = μ · P · cos α s
s sen α = μ · cos α s
s tg α = μ s μ = tg 18º s
s μ H 0,325
Atividades extras
22. a) A força de atrito é dada por: Fat. = –b · v
Fmag.
N
Isolando b, temos: b =
 M ⋅ L ⋅ T −2   M 
; no SI: [b] = kg
=
 L ⋅ T −1   T 
s
b) De acordo com o gráfico, L = 11 μm s v = 100 μm/s. Assim:
P
b)Como FR = 0 (equilíbrio), temos:
fat. = P e N = Fmag.
fat. = m · g s fat. = 0,02 · 10 = 0,2 N
Como fat. = μ · N s 0,2 = 0,5 · N
N = 0,4 N s Fmag. = N
∴ Fmag. = 0,4 N
Assim:| F |=| F at. | s k ⋅ ∆L = F at.
NB
k=
1 ⋅ 10 −12
= 1 · 10 – 6 N/m
1 ⋅ 10 −6
NA
Fat.
F
Fat.
A
NA
PB
PA
Em A: Fat. = μ · NA = 0,6 · 10 s Fat. = 6 N
6
Em B: Fat. = FR(B) s 6 = mB · a s a =
= 3 m/s2
2
Portanto:
F = FR(A; B) = (mA + mB) · a s F = (1 + 2) · 3 s F = 9 N
6
[b ] = 
F at. = 1 ⋅ 10 −8 ⋅ 1 ⋅ 10 −4 s F at. = 1, 0 ⋅ 10 −12 N
c) Novamente, de acordo com o gráfico, para v = 100 μm/s
DL = L – L0 = 1,0 μm
18. Diagrama de forças:
B
−F at.
v
23. Para termos velocidade constante:
FR = 0 s F = fat.AB + fat.BC s F = μ · NAB + μ · NBC s
s F = 0,3 · 7 · 10 + 0,3 · 2 · 7 · 10 = 21 + 42 = 63 N
24. Soma = 3 (01 + 02)
(01) (V) Na velocidade limite, temos: FR = 0
(02) (V) 18 km/h : 3,6 = 5 m/s
(04)(F) Fres. = P s 8 · 10–4 · 150 · (5)2 = m · 10 s m = 0,3 kg
(08)(F) v2 = 2 · g · ∆h = 2 · 10 · 500 s v = 100 m/s = 20 vL
Tarefa Proposta 2
Física
Resolução
FM.12
Nessa expressão, observamos que o módulo da tensão dobra de
valor se a velocidade e o raio da trajetória são duplicados.
1.d
Em S, as forças que atuam no bloco são:
9.e
N
θ
T
FRC
P
P
Como N é perpendicular a P, a única aceleração na direção do movimento é g, de cima para baixo.
sen q =
2
2
v
v
2.Fc = m ⋅
s 8.000 = 1.600 ⋅
s v=
80
R
8.000
s v = 20 m/s
20
3.a
A força centrípeta é dada por:
F
s
cent.
m⋅v2
r
Como v =
2 πr
, quanto maior o período, menor a velocidade. Como
T
Fcent. é diretamente proporcional ao quadrado da velocidade, temos:
menor período s maior velocidade s maior força centrípeta.
s
T
s FRc = T · sen θ
10. d
I.(F) A força centrípeta aponta para a esquerda.
II.(V) A FR tem característica da Fcent..
III. (F) De acordo com a inércia, a tendência do passageiro é manter-se em linha reta.
11. d
Na horizontal, temos: T = Fcent.
T =
4.Soma = 31 (01 + 02 + 04 + 08 + 16)
Todas as afirmativas estão corretas.
FRc
0, 5 ⋅ (10) 2
m⋅v2
s T =
s T = 50 N
1
R
12. e
No ponto mais alto da lombada:
FR = P – N, em que FR é a resultante centrípeta.
5.c
No ponto mais baixo, temos:
N – P = Fcent. s
m⋅v2
+m·gs
R
70 ⋅ 40 2
s N =
+ 70 ⋅ 10 s
40
s N = 2.800 + 700 s
s N = 3.500 N
13.a)
s N =
0,1
L
6.c
I.(F) A direção do vetor velocidade linear varia.
II. (F) Todo movimento curvilíneo apresenta aceleração centrípeta.
III. (V) No movimento circular uniforme, o módulo do vetor velocidade é constante.
IV.(V) A força centrípeta é perpendicular ao vetor velocidade e ao
deslocamento.
x
P
Eixo de rotação
x = L · sen θ s
s x = 0, 2 ⋅
T
s ω 2 =
Pt
PN
P
8.a
A tensão no fio é a resultante centrípeta. Assim:
7
v2
R
1
= 0,1 m s R = 0,2 m
2
b)Fcent. = m · ω2 · R s
s T · sen θ = m · ω2 · R
P
Sendo T =
, temos:
cos θ
P · tg θ = m · ω2 · R s
s 1,8 · tg 30° = 0,18 · ω2 · 0,2 s
7.b
Diagrama de forças na esfera.

FR = Pt s a é paralela a Pt .
T = Rcent. = m ⋅
θ
T
1, 8 3
s ω = 30 H 5,5 rad/s
3 ⋅ 0, 036
14. e
v = 108 km/h = 30 m/s
μ = 0,3
m = 1.720 kg
r = 200 m
Para que o veículo faça a curva em segurança, a velocidade máxima
deve ser:
Fat. = Fcent. s
Tarefa Proposta 2
Física
Resolução
2
s μ · m · g = m ⋅ v s v2 = μ · g · r s
r
s v = 0, 3 ⋅ 10 ⋅ 200 s v  24, 5 m/s
I.(F) A velocidade segura deve ser, no máximo, 24,5 m/s.
II. (V) Veja item I.
III. (V) Veja desenvolvimento.
IV.(V)
15.
c
No ápice do globo: FR = N + P
Na iminência de perder contato com o globo: N = 0 s FR = P
Como a força resultante é a resultante centrípeta, concluímos que
ela é maior ou igual ao peso do conjunto.
(V) Como o movimento é circular, sempre terá aceleração centrípeta.
(V) Ds = s – s0 = 0
(F) Apenas o módulo pode permanecer constante no MCU.
(V) Ds = 400 m s Ds = 0,400 km e Dt = 50 s
Dt =
50
= 0,833 min
60
22.a)
45°
T
0
16. b
No instante dado, temos:
P
acent. = a · cos 60° s acent. = 32 ·
Como: a cent. =
∆s 400
=
= 8 m/s
∆t
50
(F) v ra =
1
= 16 m/s2
2
b)
45°
T
v2
v2
s 16 =
s v = 4 m/s
R
1
P
FR
17. a
I.(V)
II.(F)
III.(V)
IV.(F)
 2π ⋅ R 


R
 T 
= g s T = 2π ⋅
sT=2·3·
s
R
g
∆s
⋅ g ⋅ tg θ s
2π
62, 8
⋅ 10 ⋅ tg 45º s v = 100 s v = 10 m/s
2 ⋅ 3, 14
19. a
v = 216 km/h s v = 60 m/s
a = 0,05 · g s a = 0,05 · 10 s a = 0,5 m/s2
v2
60 2
3.600
= 7.200 m ou 7,2 km
s 0, 5 =
s R=
R
R
0, 5
20.a)
T
m⋅v2
0, 10 ⋅ v 2
s 0, 30 =
s v = 0, 6 m/s
R
0, 12
∴ v = 2 π · R ⋅ f s f =
P
60 ⋅ 10
P
sT =
=
s T = 600 2 N
T
cos 45°
2
2
Tmin. = 3 · T = 1.800 ⋅ 2 N
cos 45º =
Tteste = M0 · g s 1.800 ⋅
s M0 = 254,6 kg
2 = M0 · 10 s M0 = 180 2 s
Atividades extras
(01) (V) sen 60º =
FR
s
P
0, 12 FR
=
s FR = 0, 30 N
0, 4
1
b) Fcent. =
s T = 4,2 s
c) De acordo com a figura do item b, temos:
24. Soma = 21 (01 + 04 + 16)
P(peso)
tg θ =
0, 6
= 0, 80 Hz
2 π ⋅ 0, 12
vm =
AE
45
= 51,7 m
s AC =
AC
0, 87
∆s 51, 7
=
s vm= 17,2 m/s = 62 km/h
∆t
3
(02) (F) Entre B e C, o vetor velocidade permanece constante.


(04) (V) Entre B e C, FR = 0. Então R ar e P anulam-se.
(08) (F) Na trajetória curva: Rc ≠ 0
(16)(V)
FM.13
21. V – F – V – F – V
8
4, 9
s
10
23. Soma = 24 (08 + 16)
(01)(F) A velocidade máxima não depende da massa.
(02)(F)
(04)(F) O veículo não está em equilíbrio, está acelerando.
(08)(V)
(16)(V)
Tração
θ
s
v2
= m ⋅g s
R
2
v = r ⋅ g ⋅ tg θ s v =
a cent. =
s
P
s FR = P s m ⋅
18. b
A velocidade é dada por:
s v =
FR
tg 45º =
1. O trabalho é, numericamente, igual à área da figura.
Tarefa Proposta 2
Física
Resolução
10 N
1
2m
† = A1 + A2 s † =
2
18 N
2m
18 + 10
· 2 + 2 · 18 s † = 64 J
2
2.b
O trabalho é, numericamente, igual à área do triângulo:
– 20 m
b⋅h
( ) (
)
s † = −8 ⋅ −20 s † = 80 J
2
2
3.a
Na descida: †p = + P · h = 1,0 · 10–3 · 10 · 1 = 1,0 · 10–2 J
4.e
P=
† m⋅ g⋅h
=
s P = 70 ⋅ 10 ⋅ 15 s P = 525 W
∆t
∆t
20
5.b
Pela área do gráfico:
† = Área s † =
10. a
Como P = F · v s P = 6 kW, temos:
Dobrando-se v, a força de atrito viscoso também dobra, pois são
diretamente proporcionais. Assim:
P’ = 2F · 2v s P’ = 4 · F · v s P’ = 4 · 6 s P’ = 24 kW
11. d
–8 m
†=
Quanto menor Dt, maior a potência.
∴ †E = †R e PE > PR
2 ⋅ 100
= 100 s † = 100 J
2
P =
s P = 0,5 · 103 ou P = 5 · 102 W
12. c
† m ⋅ g ⋅ h 150 ⋅ 10 ⋅ 20
=
=
s P1 = 3.000 W
∆t
∆t
10
m ⋅ g ⋅ h 250 ⋅ 10 ⋅ 10
• P2 =
=
s P2 = 1.250 W
∆t
20
m ⋅ g ⋅ h 350 ⋅ 10 ⋅ 15
• P3 =
=
s P3 = 1.750 W
30
∆t
Portanto: P2 < P3 < P1
7.b
†p = P · h s †p = 60 · 10 · 2,10 s 1.260 J
O trabalho da força peso é considerado motor quando esta tem o
sentido do deslocamento.
8.a
2 m/s
g = 10 m/s2
Pela equação de Torricelli, temos:
v2 = v 02 + 2a · Ds s
s (7)2 = (3)2 + 2 · 1 · Ds s
s 2Ds = 49 – 9 s
s Ds = 20 m
O trabalho é dado por:
† = F · d = m · a · Ds s
s † = 5 · 1 · 20 s
s † = 100 J
A potência é dada por:
P =
100
†
s P=
= 25 W
∆t
4
13. c
12 cm
C.M.
12 cm
C.M.
†P = P · h = m · g · h s †P = 25 · 10– 3 · 10 · 12 · 10– 2 s
s †P = 3 · 10– 2 J
Observação: C.M. = centro de massa.
14. ms = 60 kg
mJ = 80 kg
h = 7 m
Dt = 30 s
†
P⋅h
m⋅ g⋅h
s P=
s P=
s
∆t
∆t
∆t
60 ⋅ 10 ⋅ 7
s P=
= 140 W
30
a) P =
h
10 m/s
• v2 = v 02 + 2a · h s 22 = 102 – 2 · 10 · h s h = 4,8 m
• †P = –P · h = –m · g · h s †P = –2 · 10 · 4,8 s †P = –96 J
9.d
Os trabalhos vão ser iguais, pois, em ambas as situações, a altura
(deslocamento) atingida é relativa ao segundo andar. Com relação
†
às potências, devemos lembrar que: P =
∆t
9
∆v
7−3
s a=
= a = 1 m/s 2
4
∆t
a =
6.e
• P1 =
†
P⋅h
1 ⋅ 10 3 ⋅ 4
s P=
s P=
s
∆t
∆t
8
b)dRT é o deslocamento do rapaz/Terra
dRE é o deslocamento do rapaz/escada
dET é o deslocamento da escada/Terra
dRT = dRE + dET s
s 7 = dRE – 7 s dRE = 14 m
Como cada degrau tem 0,20 m, portanto temos 70 degraus.
c) Como o jovem subiu 70 degraus, sendo cada um de 0,2 m, logo
o deslocamento dele foi de 14 m.
∴ †1 = 80 · 10 · 14 s †1 = 11.200 J
Tarefa Proposta 2
Física
Resolução
15. •
•
Elevador subindo com velocidade constante:
FR = 0 s TM = TE – PCP
Assim: TM = (200 + 6 · 70) · 10 – 220 · 10 s TM = 4.000 N
A potência mínima do motor é:
P = TM · v s P = 4.000 · 0,5 s P = 2.000 W = 2 kW
16.b
O trabalho realizado pela força peso é:
†P = –P · h = m · g · h s
s †P = –80 · 10 · 4 s †P = –3.200 J
Portanto, o trabalho realizado pelo romeiro é:
†r = 3.200 J
Assim, o número de barras de cereais é:
1 barra
800 J
x
3.200 J
3.200
∴ x =
s x = 4 barras
800
17. d
P = F · v = 2.500 · v
Sendo s = 10 + 15 t, temos: v = 15 m/s
Portanto, a potência é:
P = 2.500 · 15 s P = 37.500 W ou P = 3,75 · 104 W
18. A vazão Q =
V
700
sQ=
= 700 m3/s
∆t
1
m
s m = μ · V s m = 103 · 700 (SI) = 7 · 105 kg
Como μ =
V
A energia potencial referente ao desnível até a turbina é:
Epot. = m · g · h s Epot. = 7 · 105 · 10 · 120 (SI) s Epot. = 8,4 · 108 J
Portanto:
E pot.
8, 4 ⋅ 10 8
s P = 8,4 · 108 W
P=
sP=
1
∆t
19. 0,3 MW = 0,3 · 106 W = 3 · 105 W
O número de rodas-d’águas é:
n =
3 ⋅ 10 5
s n = 200
2 ⋅ 750
20. Velocidade constante: módulo da força do motor igual ao módulo
da força do jato-d’água. Assim:
F = FV = C · v s F = 200 · 20 s F = 4.000 N
Em 10 s, o carrinho percorre:
d = v0 · ∆t s d = 20 · 10 s d = 200 m
Portanto, o trabalho é dado por:
† = F · d s † = 4.000 · 200 s † = 800.000 J ou † = 8 · 105 J
Atividades extras
21.a) †pilão = P · h = m · g · h s
s †pilão = 5 · 10 · 0,60 = 30 J
b)†monj. = P’ · h’ = m’ · g · h’ s
s †monj. = 30 · 10 · 2 = 600 J
Em 4,0 s, o pilão manual realiza um trabalho de 30 · 2 = 60 J
Portanto, para ter o mesmo resultado do monjolo, são necessárias dez pessoas, pois:
†monj. = 10 †pilão
22. a
De acordo com o gráfico: Pmáx. = 70 CV H 5,1 · 104 W
10
Em 10 s: P · ∆t = 5,1 · 104 · 10 s † = 5,1 · 105 W
Mas: P = F · v s 5,1 · 104 = F · 20 s F = 2,6 · 103 N
23. a
Primeiramente, calcula-se quanto vale um cavalo-vapor:
†
F ⋅ ∆s
P=
=
= F ⋅v = m⋅ g ⋅v s
∆t
∆t
s P = 75 · 10 · 1 = 750 W
∴ 1 CV = 750 W.
Como o automóvel movimenta-se com aceleração nula, ou seja, em
MRU, tem-se que:
N
F


FR = 0
Px
Py
F = Px = m · g · sen q s
s F = 1.000 · 10 · 0,1 s
s F = 1.000 N
E, agora, calculando a potência desenvolvida pelo carro:
P = F · v = 1.000 · 15 s P = 15.000 W = 20 CV
24. c
Como a subida é com velocidade constante s ∆Ec = 0.
m· g ·h
∆E
s 8,5 · 103 · 40 = m · 10 · 32 (SI)
s 8,5 · 103 =
40
∆t
m = 1.062,5 kg
Descontando-se 370 kg da massa do elevador, temos:
m’ = 1.062,5 – 370 s m’ = 692,5 kg , que é a massa dos passageiros
do elevador.
Sendo assim:
692,5
n =
s n = 9,89
70
Portanto, o número máximo de passageiros é 9.
P=
FM.14
1.a
Epot. = m · g · h. Como gT > gL s EP(T) > EP(L)
Assim, o corpo na Terra atinge o solo com energia cinética maior
que o corpo na Lua. O tempo de queda é dado por:
t q =
2⋅h
g
Portanto, como gT > gL, o corpo na Lua chega ao solo antes do corpo
na Terra.
2.e
EP(1) = m1 · g · h1 = 490 · 0,4 s EP(1) = 196 J
EP(2) = m2 · g · h2 = 539 · 0,5 s EP(2) = 269,5 J
Diferença: ∆E = 269,5 – 196 s ∆E = 73,5 J
3.b
2⋅h
2⋅5
s tq = 1,0 s
=
10
g
Epot. = m · g · h s EP(1) = 0,1 · 10 · 5 = 5 J; EP(2) = 0,2 · 10 · 5 = 10 J
Tempo de queda: t q =
4.a) P = F · v s 160.000 = 4.000 · v = 40 m/s
b) De 40 m/s para 60 m/s:
Tarefa Proposta 2
Física
Resolução
† = DEcin. s † =
m ⋅ v 2 m ⋅ v 02
−
s
2
2
 ( 60 ) 2 ( 40 ) 2 
 s
−
s † = 800 ⋅ 
2
2 
s † = 800 · 1.000 = 800.000 J
Como P =
†
† 800.000
s ∆t = =
s ∆t = 5 s
P 160.000
∆t
11. † = F · d · cos θ s † = 21 · 4 ·
Como: † = DEc s 42 = DEc s DEc = 42 J
12. m = 2 kg
k = 200 N/m
Epot. = Epot. elás.
m · g · x =
5.a) E cin. =
20 ⋅ 10 −3 ⋅ (240) 2
m⋅v2
s E cin. =
s E cin. = 576 J
2
2
† = ΔEcin. s † = –Ecin. s † = –576 J
1
s † = 42 J
2
Tarefa Proposta 2
Física
Resolução
k ⋅ x2
s
2
s x = 2m · g s x = 2 ⋅ 2 ⋅ 10 = 0, 2 m
k
200
b)† = F · d s
s 576 = Fmag. · 0,18 s
s Fmag. = 3.200 = 3,2 · 103 N
6.d
De acordo com o teorema da energia cinética:
†R = ∆Ecin. s
s †pot. = Ecin. final – Ecin. inicial s
s m · g · h = Ecin. final –
m ⋅ v 02
s
2
B
x
13. d
Na situação de equilíbrio, temos:
3 ( 0,5 )
s
2
s Ecin. final = 75 + 0,375 s Ecin. final = 75,375 J
s 3 · 10 · 2,5 = Ecin. final –
A
2
Felás. = P s k · x = P s x =
E a energia potencial elástica armazenada na mola é:
Epot. =
7.c
Sendo m1 = m2 s †1 = †2 = –m · g · h
Portanto:
†1 = †2; †1 < 0 e †2 < 0
P
k
2
1
 P
1
· k · x2 = ⋅ k ⋅  −  s
2
 k
2
s Epot. =
P2
1
P2
⋅ k ⋅ 2 s Epot. =
2k
2
k
14. d
8.b
∆E m ⋅ g ⋅ h m ⋅ g ⋅ ∆s ⋅ sen 30º
=
= m · g · v · sen 30º s
=
∆t
∆t
∆t
∆E
∆E
= 70 · 10 · 0,6 · 0,5 s
= 2,1 · 102 J/s
s
∆t
∆t
9.Soma = 3 (01 + 02)
(01)(V) a0 – 4 =
E1 =
0
s E1 =
m · (30) 2
− 0 s E 1 = 450 · m
2
m · v 22 m · v 12
m ⋅ (60) 2
−
s E2 =
− 450 ⋅ m s
2
2
2
s E2 = 1.800 · m – 450 · m s
s E2 = 1.350 · m
E 2 =
∴
1
· a7–9
2
m · v 12 m · v 02
−
2
2
E1
E
450 ⋅ m
1
=
s 1 s s E 2 = 3E 1
3
E 2 1.350 ⋅ m
E2
9 + 3 45
= 75 m
⋅
2
3, 6
(04) (F) Entre 0 e 30 s, não houve variação de energia cinética.
(08) (F) As áreas não são iguais.
15. c
No início do lançamento, a bola tem velocidade e, portanto, tem
Ecin.. À medida que sobe, sua velocidade diminui e, na altura máxima, ela é nula: Ecin. = 0. A partir daí, a bola tem sua velocidade
aumentada.
10.a) Fat.(e) = μe · m · g = 0,5 · 10 s Fat.(e) = 5 N. A intensidade da força
mínima deve ser ligeiramente maior que 5 N.
b)Fat.(c) = μc · N = 0,4 · 10 s Fat.(c) = 4 N
De acordo com o teorema da energia cinética:
16. b
Não se cria ou destrói energia; existe sempre transformação.
N
(02)(V) ∆s = Área =
†F + †Fa + †Fe = 0 s F · x – 4 · x +
c)
11
1
· kx2 = 0
2
x é o deslocamento do bloco até parar pela primeira vez.
Sendo k = 2 N/m, temos:
x ⋅ (F – 4) = x2 s x = F – 4
No equilíbrio, temos: F + Fa – Fe = 0. Assim:
F + 5 – 2 ⋅ (F – 4) = 0 s F + 5 – 2 · F + 8 = 0 s F = 13 N
17. a
Em relação ao solo, temos:

g ⋅t2 
 s
Epot. = m · g · h = m · g ⋅  h0 −

2 
s Epot. = m · g · h0 –
m⋅ g2 2
· t (O gráfico externo é uma parábola
2
com a concavidade voltada para baixo.)
E a energia cinética é dada por:
m⋅v2 m
=
⋅ (v0 + a · t)2
Ecin. =
2
2
Sendo v0 = 0, temos:
Ecin. =
24.a) vsom =
∆s
L
s 333 =
s L H 1.000 m
∆t
3
b)
Tarefa Proposta 2
Física
Resolução
1.000 m
75 cm
m ⋅ a2 2
· t (O gráfico externo é uma parábola com a concavi2
dade para cima).
1,5 cm
18. b
Como v = cte, temos:
Ecin. =
R
m · v2
20 · (0,5) 2
s Ec =
s
2
2
s Ecin. = 2,5 J
P=F ·vs
s P = 200 · 0,5 s
s P = 100 W
19. a
k ⋅ x2
Como Epot. elás. =
, podemos dizer que a energia potencial elástica
2
em função de x2 terá como gráfico uma reta ascendente com proporcionalidade direta.
20. Soma = 7 (01 + 02 + 04)
(01)(V) Epot. = M ⋅ g ⋅ (2R – R) s EP = M ⋅ g ⋅ R
(02)(V) †T = Epot. inicial – Epot.final s †T = M ⋅ g ⋅ R
(04)(V)
(08) (F) Conservação de energia mecânica:
Emec. inicial = Emec. final s
s Ecin. + Epot. = Ecin. s
s
m⋅v2
+ M ⋅ g · 2R = Ecin. s
2
s
M⋅ g ⋅R
5
+ M ⋅ g · 2R = Ecin. s Ecin. =
M·g·R
2
2
(16) (F) No ponto mais baixo: Rcin. = N – P s
s m · acin. = N – m ⋅ g s acin. ≠ g
21. d
Por semelhança, temos:
0, 015
0, 75
=
s R = 20 m s
R
1.000
s D = 2R s D = 40 m
c)Como H = 2,5D s H = 2,5 · 40 s H = 100 m
Sendo assim: Epot. = m · g · H
Epot. = 0,3 · 10 · 100 = 300 J
d) Sendo 1% de 2.000 J = 20 J, temos:
1 g
20 J
300 J
Q
300
∴Q=
= 15 g
20
FM.15
1.c
Em B e C, temos:
Emec. = m · g · hB = m · g · 4 s Emec. = 40 · m
B
B
Emec. = m · g · hC = m · g · 3,2 s Emec. = 32 · m
C
C
Houve uma perda de 0,8 m de B para C, ou seja, de 20%.
Em A e C, temos:
Emec. = m · g · hA = m · g · 5 s Emec. = 50 · m
A
Atividades extras
22. Soma = 3 (01 + 02)
(01)(V)
(02)(V) Epot.(C ) = m · g · h = 2,0 · 10 · 0,2 s Epot.(C ) = 4 J
(04)(F) v m = 2 ⋅ g ⋅ h = 2 ⋅ 10 ⋅ 0, 2 s vm = 2 m/s
A
m ⋅ v C2
E
= m · g · hC +
s E mec. = 32 ⋅ m +
C
mec.C
2
Ocorrendo perda de 20%, teremos: Emec. = 40 · m
C
Assim:
40 ⋅ m = 32 ⋅ m +
m ⋅ v C2
s 8=
2
s vC = 4 m/s ou vC = 14,4 km/h
v C2
2
m ⋅ v C2
2
s v C2 = 16 s
(08) (F) São iguais.
(16)(F) ωA = 0 e ωB =
vB 2
= 0,5 rad/s
=

4
23.a) † = DEcin. s † = Ecin. – Ecin.0
Como † = F · d s – fat. · d = –Ecin.0
Assim: μ · m · g · d =
m⋅v2
s v 2 = 2μ ⋅ g ⋅ d
2
v = 2 ⋅ 0, 4 ⋅ 10 ⋅ 2 = 4 m/s
b) E cin.0 =
m ⋅ v 02
100 ⋅ (4) 2
s E cin.0 =
= 800 J
2
2
Como †at. = Ecin. s †at. = – 800 J (negativo, pois é dissipativo).
12
2.b
Em A s Emec. = E cin.
A
0
A
+ Epot. s Emec. = m · g · hA s
A
A
s Emec. = 1 · 10 · 5 = 50 J
A
Em B s Emec. = Ecin. + E pot.
B
B
0
B
s Emec. =
B
DEmec. = Emec. – Emec. = 32 – 50 = –18 J
B
1 ⋅ (8) 2
= 32 J
2
A
3.c
Edissip. = Emec.(i) – Emec.(f)
Em relação à cabeça do macaco:
Edissip. = m · g · h – Ecin. s Edissip. = 0,2 · 10 · (5 – 0,5) – 7 s
s Edissip. = 2 J
4.a)
m = 1,2 kg
v0 = 0
v = 42 m/s
A Rar será máxima quando a velocidade da preguiça for constante.
Rar = P s Rar = m · g s Rar = 1,2 · 10 = 12 N
b) † R = ∆E c s
s †R = −
m ⋅ v 02
Velocidade constante: Fmotor = Fresist.
Portanto, o módulo da força resistente média é dado por:
† = Fresist. ⋅ d ⋅ cos 180º s
s 9 · 106 = Fresist. · 1,5 · 104 · (–1) s
9 ⋅ 10 6
s Fresist.= 600 N
1, 5 ⋅ 10 4
s Fresist. =
10. d
Em A, temos;
Emec. = Ecin. + Epot. s
s
2
1, 2 ⋅ 42 2
s †R = −
s
2
s † R = −1.058, 4 J
A
Toda essa energia foi dissipada na interação da preguiça com a
vegetação. Portanto:
Edissipada = 1,06 kJ
A
A
m ⋅ v A2
s E mec. =
+ m ⋅ g ⋅ hA s
A
2
0, 5 ⋅ (2) 2
s E mec. =
+ 0, 5 ⋅ 10 ⋅ 3 s
A
2
s Emec. = 1 + 15 = 16 J
A
Emec. , temos:
5.d
Energia mecânica inicial:
Emec. inicial =
m ⋅ v 2 0,5 ( 20 )
=
2
2
B
Emec. = Ecin. + E pot.
B
2
s Emec. inicial = 100 J
Energia mecânica final:
Emec. final = m · g · h = 0,5 · 10 · 15 s Emec. final = 75 J
Perda de energia:
Perda = Emec. inicial – Emec. final s
s Perda = 100 – 75 s Perda = 25 J
6.b
Em A, temos:
Emec. = m · g · hA = 400 · 10 · 24 = 96.000 J
A
Em B, temos:
E mec. = m · g · hB +
B
m ⋅ v B2
400 ⋅ (10) 2
= 400 ⋅ 10 ⋅ 4 +
s
2
2
s E mec. = 36.000 J
B
Portanto, foi dissipada uma quantidade de energia mecânica equivalente a 96.000 – 36.000 = 60.000 J
7.d
Energia mecânica inicial:
Emec. inicial = m · g · h = 25 · 10 · 5 s Emec. inicial = 1.250 J
Energia mecânica final:
Emec. final =
25 ⋅ ( 4 )
1
⋅m⋅v2 =
2
2
2
s Emec. final = 200 J
O módulo do trabalho das forças resistentes é dado por:
†r = Emec. inicial – Emec. final s †r = 1.250 – 200 s †r = 1.050 J
8.c
m⋅v
2
m ⋅ v 12
– F at. ⋅ d = −
2
m ⋅ v 12
d1 =
2 ⋅ F at.
Sendo v2 = 2 · v1, temos: d2 = 4 · d1
†F
at.
=−
2
9.a
Energia fornecida às rodas com 1 L de gasolina:
E = 30% · 30 · 106 s E = 9 · 106 J
13
B
s E mec. =
0
B
s
m ⋅ v B2
s
2
0, 5 ⋅ 6 2
s E mec. =
s
B
2
s Emec. = 9 J
B
B
A diferença entre Em e Em é a energia dissipada pelo atrito.
B
A
Portanto, † f = 9 – 16 = –7 J
at.
11. a
Emec. final = m · g · h = m · 10 · 68,6 s Emec. final = 686 · m s
2
 128 
1
1
m⋅v2 = ⋅m⋅
 s Emec. final = 632 · m
2
2
 3, 6 
Perda de energia:
Perda = Emec. inicial – Emec. final = 686 · m – 632 · m s
s Perda = 54 · m
Essa perda corresponde a:
s Emec. final =
54 ⋅ m
= 0,078 s 7,8%
686 ⋅ m
O valor mais próximo é 10%.
12. a
Emec. inicial + †não cons. = Emec. final
Em relação à base do escorregador:
1
· m · v2 s
2
1
s 60 · 10 · 5 + †at. =
· 60 · (8)2 s
2
m · g · h + †at. =
s †at. = 1.920 – 3.000 s
s †at. = –1.080 J = –1,08 · 103 J
13. d
I.(F) v2 = v 02 + 2 · a · ∆s s ∆s =
v 02
. A distância depende da
2⋅a
velocidade elevada ao quadrado.
II.(F) Epot. grav. = m · g · h
III. (F) Uma associação conveniente de polias (móvel e fixa) pode
multiplicar uma força e mudar sua direção.
IV.(V)
V.(V)
Tarefa Proposta 2
Física
Resolução
14. a
m = 4 kg
g = 10 m/s2
Pelo cálculo da área do gráfico do enunciado, temos:
(3 + 1) ⋅ 2
= 4 s Ds = h = 4 m
2
Em A, temos:
Área =
m⋅v2
+m⋅ g⋅h s
2
Emec. = Ecin. + Epot. =
A
A
s E mec. =
A
A
4 ⋅ (1)
+ 4 ⋅ 10 ⋅ 4 = 162 J
2
2
Em B, temos:
E mec. = E cin. + E pot.
B
B
0
B
s
B
s Ediss. = Emec. – Emec. = 18 – 162 = –144 J
A
15. d
A aceleração do sistema é dada por:
m2
20
s a = 10 ⋅
a = g ⋅
s a = 4,0 m/s2
m1 + m2
20 + 30
Em 2,0 s, a velocidade dos blocos vale (v0 = 0):
v = a · t s v = 4 · 2 s v = 8 m/s
A energia cinética do sistema, após os 2 s, vale:
Ecin. total = (m1 + m2) ·
82
v2
s Ecin. total = 50 ·
= 1.600 J
2
2
Portanto, a energia dissipada vale 1.600 J.
16. Em A, temos: E mec. = m · g · h A
A
Emec. = 50 · 10–3 · 10 · 2 s Emec. = 1 J
A
Em B, temos: E mec.
A
B
50 ⋅ 10 −3 ⋅ (2) 2
m⋅v2
=
s E mec. =
B
2
2
Emec. = 0,1 J
B
Portanto, a energia dissipada foi de 0,90 J.
17. e
Estimando-se a massa de uma pessoa adulta com 80 kg, temos:
Epot. = m · g · h s Epot. = 80 · 10 · 10 = 8 · 103 J
1
1
Epot. = 0
1
DEpot. = –8 · 103 J, cuja ordem de grandeza é 104 J.
18. c
A energia potencial elástica armazenada na mola é dada por:
1
Epot.elás. =
· k ⋅ x2
2
E a energia potencial gravitacional da bolinha é dada por:
Epot.grav.= m · g · h
Supondo que a energia potencial elástica seja transformada integralmente, temos:
1
1
⋅ k ⋅ x 12 = m · g · h1 s ⋅ k ⋅ (3 · 10 – 2)2 = 20 · 10 – 3 · 10 · 1,5 s
2
2
2.000
s k =
N/m
3
•
14
19. V – V – F – F – F
I.(V) v B = 2 ⋅ g ⋅ h = 2 ⋅ 10 ⋅ 0, 8 vB = 4,0 m/s
II.(V) †at. = Ecin.(B) – Epot.(A) s †at. =
m⋅v2
4 ⋅ (3) 2
s E mec. =
=
= 18 J
B
2
2
Ediss. = Emec. – Emec. s
B
1
⋅ k ⋅ x 22 = m · g · h2 s
2
1 2.000
· (6 · 10– 2)2 = 20 · 10– 3 · 10 · h2 s
s ⋅
2
3
2 ⋅ 10 3 ⋅ 36 ⋅ 10 − 4
s h2 =
= h2 = 6 m
6 ⋅ 20 ⋅ 10 −2
s †at. =
1
· 0,2 · (3)2 – 0,2 · 10 · 0,8 s †at. = –0,7 J
2
III. (F) No trecho BC (até parar)
†at. = –Ecin.(B) s –Fat. · d =
s d =
1
· m ⋅ v B2 – m · g · h s
2
m ⋅ v B2
1
m ⋅ v B2 s d =
s
2
2 ⋅ 0, 1 ⋅ m ⋅ g
( 3) 2
s d = 4,5 m
2
IV.(F) É negativa.
V.(F) †at. = Ecin. final – Ecin. inicial s
1
1
⋅ m ⋅ v 2 − ⋅ m ⋅ v B2 s
2
2
1
1
s –0,1 · m · g · d = ⋅ m ⋅ v 2 − ⋅ m ⋅ v B2 s
2
2
2
v 2 ( 3)
s –0,1 · 10 · 2,5 =
s
−
2
2
s –5 = v2 – 9 s v = 2 m/s
s –Fat. · d =
20. b
No ponto mais alto, temos:
Emec. = m · g · h = m · 10 · 40 s
0
Emec. = 400 m
0
No fim da queda:
Emec. = (72%) · Emec. = 0,72 · 400 · m s
0
s Emec. = 288 · m
Então:
Ecin. = Emec. s
m · v2
= 288 · m
s
s
2
s v = 576 = 24 m/s
Em km/h, temos:
v = 86,4 km/h
21. a) Até o ponto citado, a altura de queda é 4,0 m. A velocidade da
criança, nesse ponto, vale:
1
Epot. = Ecin. s m · g · ∆h = ⋅ m ⋅ v 2 s
2
s v = 2 ⋅ g ⋅ ∆h = 2 ⋅ 10 ⋅ 4 = 80
A força normal é a resultante centrípeta:
m ⋅ v 2 36 ⋅ 80
s N = 3.600 N
=
R
0, 8
b) Na água:
†R = ∆Ecin. s †P + †at. = – Ecin. inicial s
N=
1
· m ⋅ v2 s
2
1
s 36 · 10 · 1,5 – Fat. · 1,5 = – · 36 · (10,9)2 s
2
s m · g · h – Fat. · h = –
Tarefa Proposta 2
Física
Resolução
s Fat. =
540 + 2.138,58
s Fat. = 1.785,72 N s Fat. H 1.800 N
1,5
Observação: A força da água (Fat.) corresponde à força de empuxo
mais a força resistiva.
22. a)
b)
c)
A energia da bola, ao tocar o solo, é:
E = Epot. = m · g · h s E = 2 · 10 · 1 s E = 20 J
Como ela perde 50% de sua energia no choque, temos:
Ecin. = 50% · E s Ecin. = 0,5 · 20 s Ecin. = 10 J
Na subida e descida da bola, não há perda de energia. Assim,
ela toca o solo pela segunda vez com energia cinética de 10 J.
Portanto:
1
1
Ecin. =
· m · v2 s 10 =
· 2 · v2 s v = 10 m/s
2
2
Energia inicial = 20 J
1o choque (50% de perda) s Energia = 10 J
2o choque: 50% de 10 J = Energia = 5 J
3o choque: 50% de 5 J = 2,5 J
4o choque: 50% de 2,5 J =1,25 J
5o choque: 50% de 1,25 J = 0,625 J
6o choque: 50% de 0,625 J = 0,3125 J
7o choque: 50% de 0,3125 J = 0,15625 J
8o choque: 50% de 0,15625 J = 0,078125 J
A regra geral é:
E
E
E
E
E
E
E1 = 0 ;E 2 = 0 ;E3 = 0 ;E 4 = 0 ;E5 = 0 ;E6 = 0 ;
2
4
8
16
32
64
E0
E0
E7 =
;E =
128 8 256
Atividades extras
23. a) Na saída do toboágua, temos:
g · t2
s 1, 25 = 5t 2 s
2
s t = 0,5 s
Na horizontal, temos:
∆s
1,5
v x =
= 3 m/s
s vx =
∆t
0,5
b) A energia mecânica, no alto do toboágua, é dada por:
h =
Emec. = Epot. + E cin.
A
A
0
A
s Emec. = 50 · 10 · 4 = 2.000 J (considerando o nível final do toA
boágua)
Como, ao sair do toboágua, a velocidade horizontal da criança é
de 3 m/s, a energia mecânica, nesse ponto, é dada por:
Emec. = Ecin. + E pot.
B
B
B
m⋅v2
s Emec. =
s
B
2
50 ⋅ (3) 2
= 225 J
2
Assim, a energia perdida (dissipada), durante a descida do toboágua, é:
Ediss. = Emec. – Emec. = 2.000 – 225 = 1.775 J
B
B
24. a
Cilindro
fat
P
15
Pela função horária:
Ds =
a · t2
2
Assim:
1 M
∆s = ⋅ ⋅ g ⋅ T 2
2 m
De acordo com a figura 1, a energia despendida pelo camundongo,
no tempo T, corresponde ao trabalho da Fat. para um deslocamento Ds.
Ediss. = fat. · Ds s
E diss. = M ⋅ g ⋅
s E diss. =
Figura 2
1 M
⋅ ⋅ g ⋅T 2 s
2 m
1 M2
⋅
⋅ g2 ⋅T 2
2 m
FM.16
m ⋅ v 2 m ⋅ v 02
−
s
2
2
3
1, 2 ⋅ 10 ⋅ (25) 2 1, 2 ⋅ 10 3 ⋅ (5) 2
s ∆E cin. =
−
s
2
2
s ΔEcin. = 600 · 625 – 600 · 25 s
s ΔEcin. = 360.000 J ou DEcin. = 3,6 · 105 J
b) Entre 0 e 7 s: † = 0, pois v = cte.
Entre 7 e 12 s: † = DEcin. = 3,6 · 105 J
1.a) ∆E cin. =
2.a
Sistema conservativo: Emec.(1) = Emec.(2)
Para um referencial no ponto 2, temos:
Ecin.(1) + Epot.(1) = Ecin.(2) s
s Ecin.(1) + m · g · h1 =
1
⋅ m ⋅ v 22 s
2
1
⋅ 1 ⋅ v 22 s v2 = 2 2 m/s
2
3.d
2m
3
2
fat. = m · a
Com atrito
Do ponto 2 ao ponto 3: movimento retilíneo e uniforme.
Do ponto 3 em diante: movimento retilíneo uniformemente retardado até parar.
4.b
Como a mola M1 está comprimida, ela possui Epot. elás..
Para M2, a Epot. elás. = 0.
Assim:
E pot. elás. =
Camundongo
Figura 1
M
· g (IV)
m
Sem atrito
s Emec. =
A
s |a| =
s 2 + 1 · 10 · 0,2 =
s Emec. = m · g · h s
A
0
Na situação de equilíbrio:
fat. = P s fat. = M · g (II)
Para o cilindro, temos: fat. = m · a (III)
Assim, a partir de (III) e (II), temos:
m · a = M · g s
1 ⋅ 10 3 ⋅ (4 ⋅ 10 −2 ) 2
k ⋅ x2
s E pot. elás. =
s
2
2
1 ⋅ 10 3 ⋅ 16 ⋅ 10 − 4
= 8 ⋅ 10 −1 s E pot. elás. = 0, 8 J
2
Essa energia será transferida para o meio ácido.
s E pot. elás. =
Tarefa Proposta 2
Física
Resolução
5.Emola = Emec. s Epot. elás. = Ecin. + Epot. s
k ⋅ x2 m⋅v2
100 ⋅ (0, 2) 2 0, 1 ⋅ v 2
=
+m · g · h s
=
+ 0, 1 ⋅ 10 ⋅ 1, 2 s
s
2
2
2
2
s 50 · 0,04 = 0,05 · v 2 + 1,2 s
s 2 – 1,2 = 0,05v 2 s 0,8 = 0,05v2 s
0, 8
s v 2 =
= 16 s v = 4 m/s
0, 05
11. c
Na movimentação do martelo, parte da energia cinética foi transformada em energia térmica em razão do impacto com o prego.
6.a
Entre x1 e – x1, a energia cinética é constante. Entre x1 e x2 e entre
–x1 e –x2, a energia cinética diminui e a energia potencial elástica
aumenta. Como o sistema é conservativo (Emec. = Ecin. + Epot.), a soma
das energias cinética e potencial elástica permanece constante.
Sendo Epot.
k ⋅ x2
, temos:
2
Em
Ec
EP
x1
x2
7.De acordo com a conservação da energia mecânica, temos:
Emec.(alto) = Emec.(rede) s m · g · h = Epot. s
s Epot. = 70 · 10 · (9 + 1,8) = 7.560 J ou Epot. = 7,56 · 103 J
8. V – F – F – V – V
I. (V) De acordo com a conservação da energia.
h
II. (F) Não, pois está a
da base, também possui Epot..
2
III. (F) Não, pois está a uma altura inferior a h e também possui Ec.
IV.(V) E mec. = E mec.
A
s g⋅h− g⋅
s v =
B
B
s m · g · h=m · g ·
V.(V) Emec. = Emec. s m · g · h =
A
h m · v B2
+
s
2
2
h v B2
h
s v B = 2g ⋅ s
=
2
2
2
g ·h
D
m ⋅ v 02
s v 0 = 2g · h
2
9.e
Conservação de energia mecânica para um nível de referência no solo:
Epot. grav. = Epot. elás. s
m · v B2 k · x 2
s
+
A
B
2
2
2 ⋅ v B2 500(0, 1) 2
s 2 ⋅ 10 ⋅ 0, 3 =
s
+
2
2
2
2
s 12 = 2v B + 5 s 2v B = 7 s v b = 3,5 m/s
(02) (F) Pois parte foi transformada em energia potencial elástica e
parte em cinética.
(04) (V) Item (01)
(08)(V) FR = Felás. – P = k · x – m · g =
= 500 · 0,1 – 2 · 10 s
s FR = 30 N
(16) (V) Pela conservação da energia.
(32) (V) Item (01)
(64) (F) Item (01)
Emec. = Emec. s m · g · h =
13. e
F = k · x s 22,7 · 10 = k · 21 · 10–2 s
s k = 1.081 N/m = 1,081 · 103 N/m
14. c
Sistema conservativo: Emec. inicial = Emec. final
Ainda: Ecin. + 20% · Ecin. = Epot. s
s
m ⋅v2
m ⋅v2
+ 0, 2 ⋅
= m ⋅g⋅hs
2
2
(8) 2
= 10 · h s h = 3,84 m
2
Como o CM encontra-se a 0,8 m do solo, temos:
hmáx. = 3,84 + 0,8 s hmáx. = 4,64 m
s 1,2 ·
15.a) Emec. = Ec + Ep s Emec. = 2 + 12 s Emec. = 14 J
2
2
2
2
b)Emec. = Emec. s 14 = 6 + Ecin. s
2
7
7
s Ecin. = 8 J e Epot. = 6 J
2⋅m⋅ g⋅h
k
Substituindo os valores:
7
s x =
7
c)† = ΔEcin. s fat. ⋅ d = Ecin. – Ecin. s
7
12
s fat. ⋅ 5 = 0 – 8 s fat. = –1,6 N
2 ⋅ 72 ⋅ 10 ⋅ 40
s x = 24 m
100
7
16. a
Conservação de energia mecânica entre A e B, para um nível de referência em B:
Emec.(A) = Emec.(B) s Ecin. + Epot. = Ecin. s
16 m
40 m
24 m
Solo
Lmáx. = 40 – 24 s Lmáx. = 16 m
10. V – V – F – V
I.(V) A partícula transforma Ecin. em Epot..
II.(V) A partícula transforma Epot. em Ecin..
III. (F) Não ocorreu a transformação integral de Epot. para
Ecin. = E0
16
12. Soma = 60 (04 + 08 + 16 + 32)
(01) (F) Pela conservação da energia mecânica, temos:
2
1
s m · g · h =
k ⋅ x2 s
2
x =
IV. (V) Tendo as mesmas energias potenciais, em virtude da conservação da energia, terão energias cinéticas iguais e consequentemente velocidades iguais.
s
1
1
⋅ m ⋅ v A2 + m · g · (hA – hB) = ⋅ m ⋅ v B2 s
2
2
s
1
1
· (5)2 + 10 · 30 = ⋅ v B2 s vB = 25 m/s
2
2
Em B: RC = N – P s
s R =
v B2
2, 5 ⋅ g
=
m ⋅ v B2
= 3,5 ⋅ m ⋅ g − m ⋅ g s
R
( 25 )
2
2, 5 ⋅ 10
s R = 25 m
Tarefa Proposta 2
Física
Resolução
17. c
21. Pela conservação da energia mecânica, temos:
A
Emec. = Emec. s m · g · hA =
A
L
Tmáx.
m
B
P
Adotando o ponto B como referência, temos:
Emec.(A) = Emec.(B) s Epot.(A) = Ecin.(B) s
m⋅v2
s v2 = 2 · g · L
2
Substituindo em (I):
2⋅ g ⋅L

+ g  s Tmáx. = 3 · m · g
Tmáx. = m 
 L

18. c
†R = ∆Ecin. s †pot. + †at. = Ecin. final s


H
s m ⋅ g ⋅ H – μ · m ⋅ g · cos 60º ⋅
+ μ ⋅ m ⋅ g ⋅ d  = Ecin. final s


sen 60°
s x2 =
s Ecin. final = 20 · m · g ⋅
(
3 − 1)
mv 2
Para raio máximo s RC = P s
=m·gs
R
sv= R⋅ g
Conservação de energia:
Ecin. inicial = Epot. + Ecin. final s
mv 2
s
2
m⋅R ⋅ g
s 20 · m · g ( 3 − 1) = mg · 2R +
s
2
5⋅ m⋅ g ⋅R
s R = 8 ⋅ ( 3 − 1) m
s 20 ⋅ m ⋅ g ⋅ ( 3 − 1) =
2
(
100 ⋅ x 2
s
2
3 − 1) = m ⋅ g · 2R +
19. a
Na trajetória de subida, temos que:
1
= 1.500 m
H = Ds · sen 30° s H = 3.000 ·
2
Assim, como †P = –DEpot., temos:
1,5 · 108 = m · g · H s 1,5 · 108 = m · 10 · 1.500 s
1,5 · 10 8
kg = 10.000 kg ou ainda
15.000
m = 10 toneladas
s m =
8
= 0,16 s x = 0,4 m
50
ou ainda x = 40 cm
Atividades extras
22. Pela conservação da energia, após a compressão máxima da mola,
teremos:
E mec. 0 = E M s m · g · h =
k ⋅ x2
+ m · g · (0,8 – x) s
2
2
s 0,5 · 10 · 2,8 = 100 ⋅ x + 0,5 · 10 · (0,8 – x) s
2
s 14 = 50x2 + 4 – 5x s 50x2 – 5x – 10 = 0 s
s 10x2 – x – 2 = 0 s x’ = 0,5 m
x’’ = –0,4 m (Não convém.)
Assim: Lmin. = (0,8 – 0,5) m = 0,3 m
2R · sen w
23.
R
1

20 3 1 2
1
3 − ⋅m⋅ g ⋅
⋅ ⋅
+ ⋅ m ⋅ g ⋅ 20  s
2
2 3 2
2

s m ⋅ g · 20 ·
s 20 · m · g ⋅
s 0,5 · 10 · 1,6 =
k ⋅ x2
s
2
s 8 = 50x 2 s
No ponto B (ponto mais baixo da trajetória), a tração é máxima e
dada por:
v 2

m⋅v2
s Tmáx. = m ⋅  + g  (I)
Tmáx. – P =


L
L
sm·g·L=
B
R · cos w
w
• Para o bloco ultrapassar o rasgo, o alcance, no lançamento oblíquo, deve ser 2R ⋅ sen ϕ. Assim:
2R ⋅ sen ϕ
v 2 · sen ϕ
v 2 · sen ϕ · cos ϕ
s 2R · sen ϕ =
s
9
9
Rg
(I)
cos ϕ
• No ponto no qual o bloco perde o contato, a altura, em relação
ao solo, é h’ = R + R ⋅ cos ϕ (II)
• Pela conservação da energia mecânica:
Emec.i = Emec.f s
m · V2
s mgh = mgh’ +
s
2
s v 2 =
s gh = g(R + R ⋅ cos ϕ) +
Rg
s
2cos ϕ

1 

s h = R ⋅  1 + cos ϕ +
2cos ϕ 

24. c
A1
N
F
A2
20. d
Ecin. (máx.) = Epot.
1
⋅m⋅v2 = m⋅ g ⋅R s v2 = 2⋅ g ⋅R
2
No ponto mais baixo da trajetória (energia cinética máxima), temos:
v 2 2 gR
a
=
=
s a cent. = 2 ⋅ g
cent.
R
R
s
17
P
α
A3
FR = Px – F s m · a = m · g · sen α – k · x1 s
s x 1 =
m ⋅ ( g ⋅ sen a − a )
k
(I)
Velocidade em A2: v2 = v 02 + 2 · a · ∆x s v2 = 2 · a · x1
Em A3: v = 0
Tarefa Proposta 2
Física
Resolução
Conservação de energia mecânica entre A2 e A3:
1
1
⋅ m ⋅ v2 + m · g · x2 · sen α +
· k ⋅ (x1 – x2)2
2
2
Lembrando-se de que v2 = 2 · a · x1, temos:
m · a · x1 + m · g · x2 · sen α +
1
⋅ k · x 12 =
2
1
1
= ⋅ k ⋅ x 12 + k · x2 · x1 + ⋅ k ⋅ x 22
2
2
Substituindo (I) nessa última expressão:
m ⋅ a ⋅
( m ⋅ g ⋅ sen a − ma )
k
s
k
+
1
⋅ k ⋅ x 22 s
2
( m 2 ⋅ a ⋅ sen a − a )
1
⋅ k ⋅ x 22 − m ⋅ a ⋅ x 2 −
=0
2
k
x 2 =
m ⋅ a + m2 ⋅ a2 + 4 ⋅
k m 2 ⋅ a ⋅ ( g ⋅ sen a − a )
⋅
2
k
s
k
m⋅a m
+
· a ⋅ ( 2 ⋅ g ⋅ sen a − a )
k
k
Portanto, xmáx. vale:
xmáx. = x1 + x2 s
m ⋅ g ⋅ sen a m ⋅ a m ⋅ a m
s xmáx. =
−
+
+ · a ⋅ ( 2 g ⋅ sen a − a ) s
k
k
k
k
s x2 =
s x =
9.Na figura, temos:
λ = 4 m e T = 8 s
Então:
v = λ · f = λ ⋅
+ mg · x2 · sen α =
( m ⋅ g ⋅ sen a − m ⋅ a )
= k · x2
Pelo gráfico yOt, temos: T = 10 s
1
1
f = s f =
= 0, 1 Hz
T
10
v = λ · f s v = 20 · 0,1 s v = 2 m/s
m ⋅ g ⋅ sen a + m ⋅ a ⋅ ( 2 ⋅ g ⋅ sen a − a )
k
FO.05
1.a
I.(V)
II.(F) O som é mecânico e não se propaga no vácuo, e a luz é
eletromagnética.
III.(F) A luz é eletromagnética, e o som não.
1
4
s v=
= 0,5 m/s s v = 50 cm/s
T
8
10. b
Pontos em fase: A e D
11. V – F – V – F – F – F – V
1
Hz s T = 5 s
5
I.(V) v = λ · f s 2 = 10 · f s f =
II. (F) Ver item anterior: f =
III.(V) vR = 5 m/s s vR = λ · f ’ s 5 = 10f ’ s f ’ =
1
Hz
5
IV. (F) Veja itens anteriores.
V.(F) A distância depende da velocidade relativa às ondas e do
comprimento de onda.
VI. (F) Ver item anterior.
VII.(V) vR = 1 m/s s v = λ · f ’ s 1 = 10 · f ’ = 0,1 Hz ou T = 10 s
12. De acordo com o gráfico: A = 2 cm e T = 4 s
Assim:
1 1
s f = 0,25 Hz
• f = =
T 4
• v = λ · f s v = 0,80 · 0,25 s v = 0,2 m/s
13. d
f = 10 Hz s v = λ · f s v = 8 · 10 = 80 cm/s
2.b
Como o tempo entre uma batida e outra diminui, a frequência aumenta. Período e frequência são inversamente proporcionais.
14. T = 0,40 s
a)a = 7,5 cm (Veja gráfico.)
λ = 28 cm (Veja gráfico.)
3.b
1
1
= 2,5 Hz
s f =
T
0, 4
v = λ · f s v = 0,28 · 2,5 = 0,7 m/s
b) f =
T = 0,5 s s f =
1
1
s f = 2 Hz
=
T 0,5
4.c
v = λ ·
λ 80
1
s T = =
= T = 4,0 s
v 20
T
5.a
Ondas de rádio são eletromagnéticas. FM é sigla de frequência modulada.
6.d
A frequência é característica da onda que não se altera, mesmo que a
onda mude de meio.
7.v = λ · f s v = 4,0 · 40 s v = 160 m/s
8.a
Pelo gráfico xOy, temos: λ = 20 m
18
1
Hz ou T = 2 s
2
15. d
a) (F) As ondas sonoras não se propagam no vácuo.
b)(F) A velocidade correta é 300.000 km/s.
c) (F) As ondas sonoras são longitudinais.
d)(V)
e)(F) A frequência não corresponde ao tempo de cada vibração e sim
ao número de vibrações geradas na unidade de tempo.
16. b
d = vs · ∆t s d = 340 · 3 s d = 1.020 m
17. Soma = 76 (04 + 08 + 64)
(01) (F) São ondas eletromagnéticas.
(02) (F) As ondas transportam apenas energia, e não massa.
(04)(V) O meio material altera a velocidade de propagação e, portanto, o comprimento de onda.
Tarefa Proposta 2
Física
Resolução
(08)(V) A frequência depende da fonte que a produz.
(16) (F) Veja item 04.
(32) (F) As velocidades variam de acordo com o meio.
(64)(V) v = λ · f s 3 · 108 = 3 · 108 · 103 · λ s
1
s λ =
= 10– 3 m ou 0,1 cm
10 3
1
18. a) De acordo com as figuras, 0,10 s corresponde ao tempo de
4
da oscilação completa. Assim: T = 0,40 s
1
1
f = =
s f = 2,5 Hz
T 0, 4
b) Da figura: λ = 100 cm = 1 m. Portanto:
v = λ · f s v = 1 · 2,5 s v = 2,5 m/s
19. b
Pela figura, entre duas contrações, temos: 20 mm
∆s
20
Assim: v =
s 25 =
s ∆t = 0, 8 s
∆t
∆t
0,8 s
1 bat
x
60 s
∴ x = 75 bat/min.
20. b
Sendo v = λ · f, temos:
I. 3 · 108 = 3 · 107 · f s f = 10 Hz (alfa)
II. 3 · 108 = 6 · 108 · f s f = 0,5 Hz (delta)
21.
e
1 – frequência
2 – período
3 – comprimento de onda
4 – amplitude
22. a
As velocidades das três ondas são iguais:
∆s
12
s vA = vB = vC =
= 6,0 m/s
∆t
2, 0
Comprimentos de onda:
A: 4 · λA = 12 s λA = 3,0 m
B: λB = 12 m
C: 2 · λC = 12 s λC = 6,0 m
Frequências:
vA = λA · fA s 6 = 3 · fA s fA = 2,0 Hz
vB = λB · fB s 6 = 12 · fB s fB = 0,50 Hz
vC = λC · fC s 6 = 6 · fC s fC = 1,0 Hz
∴ fA > fC > fB s TA < TC < TB
vA = vB = vC =
Atividades extras
23. a
I.(V)
II. (V) Sendo d o raio da frente de onda esférica, temos:
P
Aesf. = 4π · d2. Assim: I = P s I =
4π · d 2
Aesf.
III.(F) Como dM = 0,387dT e a potência da fonte (Sol) é a mesma
para os dois, temos:
IT · AT = IM · AM s
s 1,35 · 103 · 4π · d T2 = IM · 4π · (0,387)2 · d T2 s
s IM =
19
1, 35 ⋅ 10 3
s IM = 9,014 · 103 W/m2
0, 1498
IV.(F) Ele pode ser considerado fonte puntiforme, desde que a
distância correspondente ao raio da frente de onda seja muito
maior que seu próprio raio.
24. a) v = λ · f s 340 = 0,85 · 10– 2 · f s f = 4 · 104 Hz
b)∆tT = ∆tar + ∆tágua s 0,5 =
s 0,5 = 0,2 +
68
h
+
s
340 1.400
h
s h = 420 m
1.400
c) As ondas sonoras são ondas mecânicas.
FO.06
1.Soma = 15 (01 + 02 + 04 + 08)
Todas as afirmativas estão corretas.
2.d
Fenômeno de difração de ondas.
3.d
Na reflexão de um pulso em uma corda:
• se a extremidade for fixa, haverá inversão de fase;
• se a extremidade for livre, a fase é a mesma.
4.c
Os raios X têm frequência mais alta que as ondas ultravioleta.
5.b
Nas fendas: difração.
Na região entre B e C: interferência.
6.d
a) (F) Nas ondas longitudinais, as vibrações ocorrem na mesma
direção de propagação da onda.
b) (F) Nas ondas transversais, as vibrações ocorrem em uma direção perpendicular à direção de propagação da onda.
c) (F) Ondas luminosas e ondas de rádio são ondas transversais.
d)(V)
e)(F)
7.a
I.(V) Nas ondas transversais pode-se eliminar uma direção de
vibração com a polarização.
II. (F) Ambas podem sofrer interferência.
III.(F) A onda sonora é longitudinal e pode apresentar efeito
Doppler.
8.d
f1 = 1.000 Hz
v1 = 340 m/s
f2 = 1.000 Hz
v2 = 2.000 m/s
v
λ2 = s
f
2.000
s λ2 =
=2m
1.000
A frequência permanece a mesma ( f = 1.000 Hz).
9. v =
∆s
2L
2L
s v=
s ∆t =
∆t
∆t
v
Tarefa Proposta 2
Física
Resolução
10. c
v
v
Na refração: 1 = 2
λ1 λ2
Assim, temos:
• v1 = λ1 · f1 s 10 = λ1 · 5 s λ1 = 2 m
• 10
5
=
s λ2 = 1 m
2
λ2
11. c
Analisando-se o gráfico, encontram-se as interferências construtivas
e destrutivas, ora somando, ora subtraindo suas amplitudes.
12. c
Na reflexão e na refração de uma onda, a frequência não se altera.
13. d
Observam-se as leis da reflexão, em especial: iˆ = rˆ .
14. e
Ocorre interferência destrutiva, pois o pulso A, ao sofrer reflexão,
tem sua fase invertida.
15. e
As ondas sonoras, assim como as ondas eletromagnéticas, sofrem
difração.
16. d
a) (F) As ondas geradas em abalos sísmicos são mecânicas e não
eletromagnéticas.
b) (F) No vácuo, a velocidade é constante.
c) (F) Na refração, a frequência não se altera.
d) (V) Sendo v = λ · f e como v diminui (refração) e f não se altera,
λ diminui.
17. O primeiro mínimo ocorre quando:
λ
v
340
=
∆ =
s ∆ = 0,17 m
s ∆ =
2
2 ⋅ f 2 ⋅ 1.000
Na figura, temos (para ângulos pequenos):
y
s
sen θ = tg θ =
D
D ⋅ ∆ 10 ⋅ 0, 17
∆ y
s
s y=
s
=
=
2
D
2
2
s y = 0,85 m = 85 cm
18. a
O comprimento de onda aumenta, pois é diretamente proporcional à velocidade. A frequência da onda é caracterizada pela fonte
e, portanto, não sofre alteração.
19. d
A frequência permanece a mesma, pois depende da fonte.
20. a) v = λ · f s 340 = λ · 160 s λ = 2,125 m
b) Na refração, a frequência não se altera. Portanto: f = 160 Hz
c)v = λ · f s 1.450 = λ · 160 s λ = 9,06 m
21. c
Mínimos para uma difração de fenda única:
y =
m⋅λ
⋅ D , em que: D = distância da fenda ao anteparo;
a
a = largura da fenda; m = ordem do mínimo.
20
De acordo com a figura:
y = 1 cm = 1 ⋅ 10–2 m; m = 1; λ = 500 μm = 500 ⋅ 10–6 m e
D = 10 cm = 10 ⋅ 10–2 m
Assim:
m ⋅ λ ⋅ D 1 ⋅ 500 ⋅ 10
a =
=
s a = 5.000 nm = 5 μm = 5 · 10–3 m
y
1
Atividades extras
22. d
I.Variam as grandezas: velocidade e comprimento de onda.
A frequência se mantém constante, pois é determinada pela
fonte que a produz.
II. Esse ponto (foco) é, para um espelho plano, impróprio, e está
“posicionado” no infinito.
III. Ambos podem ocorrer.
23. Soma = 7 (01 + 02 + 04)
(01) (V) Ambos os pulsos têm 2 cm de amplitude.
(02) (V) Após o processo de interferência, os pulsos seguem suas direções
e sentidos de propagação com as mesmas amplitudes iniciais.
(04) (V) Nesse momento, a interferência será destrutiva, pois os
pulsos estão em inversão de fase.
(08) (F) Veja item 04.
24. a
Luz
h
θ
x
tg θ =
h
s h = x · tg θ
x
Para interferência construtiva: 2h = m ⋅
λ
n
Sendo x = m · e, temos:
λ
2 ⋅ m ⋅ e ⋅ tg θ = m ⋅
n
Para ângulos pequenos: tg θ = θ. Assim:
2 · e · θ =
λ
λ
sθ=
n
2⋅n⋅e
FO.07
1.d
Ao ser trocada em B, serão formados nós em E e G e, portanto, os
pontos em que vibram os papéis são D e F.
2.a
a)(V)
b) (F) As ondas são mecânicas e não eletromagnéticas.
c)(F)
d) (F) As ondas sonoras difratam.
e) (F) As ondas sonoras não se propagam no vácuo.
3.Soma = 22 (02 + 04 + 16)
(01) (F) As ondas sonoras não se propagam no vácuo.
(02)(V)
(04)(V)
(08)(F) O eco é causado pela reflexão de ondas sonoras.
(16)(V)
Tarefa Proposta 2
Física
Resolução
4.d
O maior comprimento é obtido quando na corda tem-se o 1º harmônico:
10. d
v = λ · f. Sendo v1 = v2, temos:
λ1 · f1 = λ2 · f2 s
s
Então:  =
Assim: 50 =
λ
2
1
= 0,05 · 106 Hz ou
20 ⋅ 10 −6
50.000 Hz, que gatos e morcegos conseguirão ouvir.
λ
s λ = 100 cm
2
Sendo assim, a frequência é: f =
6.c
f3 = 360 Hz (3º harmônico) s f3 = 3f1 = 120 Hz
O próximo harmônico (f4) é dado por: f4 = 4f1 s f4 = 480 Hz
Sendo assim, teremos cinco nós e quatro ventres com frequência
de 480 Hz.
7. ∆t = 100 ms s v =
∆s
∆s
s 330 =
s ∆s = 33m , porém
100 ⋅ 10 −3
∆t
esse deslocamento compreende a ida e a volta e, portanto:
∆s
s 16,5 m.
2
8.e
A alternativa incorreta é a e.
Maior frequência implica maior energia.
9.a) f = 440 Hz
L = 0,6 m
Portanto, na condição inicial: L =
λ =
3
3
⋅ λ s 0, 6 = ⋅ λ
4
4
2, 4
= 0, 8 m
3
v = λ ⋅ f s v = 0,8 ∙ 440 s v = 352 m/s
b)λ = 0,8 m
13. d
14. e
I.(F) A velocidade depende do meio de propagação.
II.(V)
III.(V)
IV.(V)
15. b
16. b
O túnel funciona como um tubo aberto. Assim:
n⋅v
n ⋅ 340
s 68 =
s n = 12
2⋅
2 ⋅ 30
17. L = 2,5 cm
v = 340 m/s
(tubo fechado) s f =
s f =
0,6 m
v
4
340
= 3.400 Hz ou 3,4 · 103 Hz
4 ⋅ 0, 025
18. b
90 km/h = 25 m/s
Como a fonte sonora aproxima-se do observador em repouso:
f 0 =
v
⋅f s
v −vf f
s f 0 =
c)
21
12. Soma = 5 (01 + 04)
(01)(V)
(02)(F) É longitudinal.
(04)(V)
(08)(F)
f =
Observação: em nosso material, consideramos a velocidade do som
no ar igual a 340 m/s, portanto, na teoria, encontramos um valor de 17 m
para a distância de eco.
λ 1 20.000
λ
s 1 = 1.000
=
λ2
λ2
20
11. d
Pelo gráfico: T = 20 μs ou 20 · 10– 6
5.b
I.(F) A velocidade da onda em um meio é constante.
II.(V)
III.(F) O comprimento de onda também se altera.
IV.(F) A interferência é destrutiva.
V.(F) A polarização ocorre com as ondas eletromagnéticas.
VI.(V)
VII.(F) O eco ocorre por reflexão.
d=
λ1
f
= 2 s
λ2
f1
340
⋅ 500
340 − 25
19. a
Na mesma oitava, o som lá tem maior frequência que o som ré e,
portanto, tem menor comprimento de onda.
“A frequência é inversamente proporcional ao comprimento de
onda.”
Além disso, todos os sons produzidos no ar e num mesmo ambiente
terão mesmas velocidades.
Tarefa Proposta 2
Física
Resolução
FO.08
20. c
L
L
Q
P1
x
I1 = I2
P2
y
2
d 
P
P
P
I1 = I2 s 1 = 2 s 1 =  1  s
A1 A 2
P2  d 2 
1.a
Em A: x = R · cos θ0 e v = ω · R · sen θ0
Em P: v = –ω ⋅ R · cos θ0
2.e
m = 4 kg
k = 25π2 N/m
O período é dado por:
2
x
x
s 4 =   s = 2
y
y
Sendo x + y = ,, temos:
T = 2π ⋅
m
s
k
4
2
4
s T = 2π ⋅
= = 0, 8 s
25π 2
5π 5
s T = 2π ·
2
x
x + = L s x = ⋅ L
2
3
P
P
P
=
s r2 =
s
A 4π ⋅ r 2
4π ⋅ I
40
s r2 =
sr=4m
4 ⋅ π ⋅ 0, 2
21.a) I =
I
s
b)β = 10 · log
I0
Tarefa Proposta 2
Física
Resolução
3.a) Pela equação, temos:
x(t) = A · sen (ωt)
Sendo assim: x(t) = 4sen (4πt) s A = 4 m e ω = 4π rad/s
Se ω = 2 π ⋅ f s f =
T =
4π
ω
s f =
s f = 2 Hz
2π
2π
1
= 0,5 s
2
b)
I
I
s log
=6 s
s 60 = 10 · log
10 −12
10 −12
I
s
= 10 6 s I = 10– 6 W/m2
10 −12
x (m)
4
22. λar = 2,0 m
var = 340 m/s
λágua = 8,0 m
1
0,5
0,25
340
= 170 Hz
2
para a água s fágua = far s f = 170 Hz
b)vágua = λágua · f s vágua = 8 ∙ 170 = 1.360 m/s
0,75
t (s)
a)var = λar · f s f =
Atividades extras
23. a) De acordo com os gráficos, temos que:
Dt = 40 μs
b) Para o intervalo de tempo de 40 μs, o pulso percorre uma distância de 2D. Sendo assim:
2D
∆s
s 1.200 =
v =
s 0,048 = 2D
40 ⋅ 10 −6
∆t
D = 0,024 m = 24 mm
c) Para encontrarmos λ, basta usarmos a equação fundamental da
ondulatória:
v = λ · f s 1.200 = λ · 1,5 · 106 s
s λ =
1.200
= 8 · 10– 4 m = 0,8 mm
1,5 ⋅ 10 6
24. b
A velocidade da onda é:
∆s 12
=
s v = 24 m/s
v =
∆t 0,5
Sendo v =
T
s 24 =
d
60
s
d
Observando o gráfico, vemos que, após o início do movimento,
o corpo retorna a x = 0 em 0,25 s.
c)E cin. é máxima quando v é máxima. Isso ocorre sempre que
x(t) = 0.
4.a
F=k·x
Para F = 20 N, temos: x = A. Assim:
• 20 = 100 · A s A = 0,2 m
• vmáx. = ω · A =
2π
2π
⋅A=
⋅ 0, 2 s vmáx. = 0,1 m/s
T
4π
5. V – V – V – F – F
I.(V) T = 4 s
II.(V) A = 20 cm
III.(V)
IV.(F) A velocidade é positiva, nula e negativa.
V.(F) f =
1 1
=
s f = 0,25 Hz
T 4
6.a) T = 2 π ·
L
g
60
60
s d=
d
576
A massa do fio é:
Se L’ = 4L, temos: T’ = 2 π ·
m
60
720
5
d =
s m=d·,sm=
⋅ 12 =
s m = kg

576
576
4
b)Como T =
s 576 =
22
4L
= T ’ = 4π ·
g
L
g
Portanto, o período dobraria.
1
, a frequência seria reduzida à metade.
f
7.a
A energia mecânica é constante e dada por:
m
T = 2 ⋅ π ⋅
k
Para m’ = 4 ⋅ m, temos: T ’ = 2 ⋅ T
Emec. = k ⋅
Sendo f =
f
f ’ =
2
9. V – F – V – V – F
I.(V)
2π
2⋅3
⋅ A s v máx. =
· 6 · 10–2 = 0,18 m/s
T
2
II.(F) A amplitude é 6 cm.
III.(V)
= 0,54 m/s2
1 1
= s f = 0,5 Hz
T 2
IV.(V) f =
V.(F) F = m · a = m · ω2 · A · cos θ
m · v2
1⋅ v 2
s 200 =
s v = 20 m/s
2
2
11. c
L
, temos:
g
 L 
L


2
g 
 1
g
T
=
s   = 
L2 
2
2T
L


2π ⋅ 2
g
 g 
2
s
1 L
s =
s L2 = 4L e, portanto, deve ser aumentado de 3L.
4 L2
12. Soma = 25 (01 + 08 + 16)
(01)(V) x = A · cos (ω ⋅ t + θ0)
(02)(F) v = –ω · A · sen (ω ⋅ t + θ0)
(04)(F) F = m · ω2 · A · cos (ω · t + θ0)
m
k
(16)(V) F = k · x
2π
2π
⋅ A s vmáx. =
⋅ 0, 1 s vmáx. = 0,2 m/s
T
π
14. c

π
x = 2 · cos  3 ⋅ t +  Portanto: A = 2 m

2
23

, temos:
g
2
48, 3
s gx = 4,9 m/s2
9, 86
Assim:
g
g
4, 9
1
s x =
x =
gT
gT 2
9, 8
18. a
Como x = A · cos (ω · t + ϕ0), temos:
A = 0,050 m
2π
2π
sT=1s
s 2π =
T
T
19. c
De acordo com o gráfico: t = 0 s y = 2 cm
Assim:


π
π
y = A · cos  ω ⋅ t +  s 2 = A · cos  0 +  s


3
3
1
s A = 4 cm
2
A energia total é dada por:
s2=A·
E =
k ⋅ A 2 20 ⋅ ( 4 ⋅ 10 −2 )
=
2
2
2
s E = 16 · 10– 3 J
20. e
m
k
II.
(F) A força peso é a responsável por provocar a distensão na mola.
III.(V)
IV.(V)
13. a) T = 2 ⋅ π ⋅ m s T = 2 ⋅ π ⋅ 1 s T = π s
4
k
m⋅v2
s 40 = 0,1 · v2 s v = 20 m/s
2
2
g x = 4 ⋅ π ⋅  = 4 ⋅ ( 3, 14 ) ⋅ 21, 225 s
T2
 15, 7 


 5 
ω =
2π ⋅
b)vmáx. = ω ⋅ A =
Epot. = 2Ec s 40 = 2 ⋅
s gx =
10. e
Na posição de equilíbrio: Ecin. = 200 J
(08)(V) T = 2 ⋅ π ⋅
k ⋅ x2
2 ⋅ 10 3 ⋅ (2 ⋅ 10 −1 ) 2
s E pot. =
= 4 ⋅ 10 s
2
2
s Epot. = 40 J (máxima)
Pela conservação da energia, num ponto em que Ecin. = Epot. , temos:
16. Epot. =
2
2 ⋅ 3
2⋅ π
amáx. = ω 2 ⋅ A = 
 · 6 · 10–2 =
 ⋅ A s a máx. = 
 2 
 T 
Como T = 2π ·
Após 3.600 oscilações completas, temos:
∆t = 3.600 · 0,8 s ∆t = 2.880 s = 48 min
17. Sendo T = 2 ⋅ π ⋅
2
Assim: Ecin. =
s Emec. = 64 J
2π
5π 2π
s
=
s T = 0,8 s
T
2
T
ω =
8.a
Existem dois máximos de Epel e um mínimo que corresponde ao
ponto de máxima Ec.
2
15. c
1
:
T
vmáx. = ω ⋅ A =
(2)
A2
= 32 ⋅
2
2
I.(F) O período para o MHS é dado por T = 2π ·
Atividades extras
21. a) ω = 2π ∙ f s ω = 5π rad/s
y(x) = A ∙ sen (k ∙ x + θ0), em que θ0 é a fase inicial (espacial)
y(x) = 1,5 ∙ sen (k ∙ x + θ0)
Tarefa Proposta 2
Física
Resolução
Do gráfico:
Para x = 0 s y = 0
y(0) = 1,5 ∙ sen (k ∙ 0 + θ0) s
s 1,5 ∙ sen (k ∙ 0 + θ0) = 0 s
s sen (θ0) = 0 s θ0 = 0
Para x = 1 s y = 1,5
y(1,5) = 1,5 ∙ sen (k ∙ 1 + θ0) s
s 1,5 ∙ sen (k ∙ 1 + θ0) = 1,5 s
O intervalo de tempo pode ser calculado como:
i = ∆Q s 10.000 = 20 s ∆t = 0, 002 s
∆t
∆t
2.d
R =
3.b
U = R · i s 104 = 2 · 106 · i s i = 5 · 10–3 A
π
s sen (k) = 1 s K =
2
π 
Portanto: y(x) = 1,5 ∙ sen  ⋅ x 
2 
4.a
b)y(t) = A ∙ cos (ω ∙ t + φ0) em que φ0 é a fase inicial (temporal)
Para A = 1,5 s φ0 = 0
Portanto: y(t) = 1,5 ∙ cos (5π ∙ t)
c)v = λ ∙ f s f =
v
10
=
s f = 2,5 Hz
λ
4
22.a) ω = 2π rad/s
Como ω = 2π · f s 2π = 2π · f s f = 1 Hz
b)Como B e C são os pontos médios de AD e DA ' s Dϕ = 60°
(Veja figura.)
Δs
i =
A’
C
Δϕ
∆Q
8, 1 ⋅ 10 15 ⋅ 1, 6 ⋅ 10 −19
= 1,3 · 10 – 3 A ou 13 · 10 – 4 A
s i=
∆t
1
5.i = 1,6 · 10– 2 A
−19
i = ∆Q s i = n ⋅ e s 1, 6 ⋅ 10 −2 = n ⋅ 1, 6 ⋅ 10
∆t
∆t
3.600
n = 3,6 · 1020 elétrons
2 e–
1 molécula
x
3,6 · 1020 e–
20
∴ x = 1,8 · 10 moléculas
6.a
R =
60°
V
40
=
s R = 200 Ω
i 0, 2
U
n ⋅ 10 − 4
s 2.000 =
s n = 400.000
i
20 ⋅ 10 −3
60°
D
B
A
x
7.Soma = 37 (01 + 04 + 32)
U
.
i
(02)(F) A resistência não pode aumentar sem que a tensão se modifique.
(04) (V) Entretanto, a variação entre tensão e corrente não é linear.
(08)(F) A relação é linear.
(16) (F) Aumentando-se a tensão, a corrente deve aumentar.
(32)(V) A resistência é constante.
(01) (V) Apresenta razão
Como ∆j = 60° s ∆j =
π
rad e w = 2π rad/s, temos:
3
π
∆ϕ
1
π
1
ω=
·
s s ∆t = s
s 2 π = 3 s ∆t ·
3
∆
∆
2
t
t
π
6
23. e
De acordo com as figuras dadas, a energia mecânica (cinética +
potencial) permanece constante.
8.c
Para U = 120 V, temos i = 0,5 A. Assim:
24. a) v = 5,0 cm/s
Encontramos o período por meio da distância entre dois máximos sucessivos e a velocidade da esteira.
Para U = 10 V, temos i = 0,1 A. Assim:
U 10
R = =
s R = 100 Ω
i
0, 1
Portanto, o fator é aproximadamente:
240
f =
s f = 2,4 Hz
100
20
20
∆s
s Dt =
s5=
= 4,0 s
∆t
5
∆t
∴ T = 4 s
b) Com o aumento do comprimento do fio, tem-se alteração no
período de oscilação.
v =
Como: T = 2π ·
T’ = 2π ·

, quadruplicando o comprimento, temos:
g
4
s T’ = 2 · 2π ·
g

s T’ = 2 T
g
Então: T’ = 8 s, portanto:
Ds = v · T’ s Ds = 5 · 8 = 40 cm
FE.05
1.c
São conflitantes, com relação às descargas elétricas ocorridas no ar.
24
R =
U 120
=
s R = 240 Ω
i
0,5
9.d
I. (V) Resistor não tem polaridade.
II.(V) U = R · i
III.(F) R = ρ ⋅

é diretamente proporcional ao comprimento,
A
mas inversamente proporcional à área.
10. a
ρ⋅L
A
Dobrando-se o raio da seção transversal e dobrando-se também o
comprimento do fio, temos:
A’ = 4 · A e L’ = 2 · L
R =
Tarefa Proposta 2
Física
Resolução
Assim:
ρ⋅2⋅L
1 ρ⋅L
R
R’ =
s R’ = ⋅
s R’ =
4⋅ A
2 A
2
a) (F) Se L’ = 2 · L s R’ = 2 · R e i’ =
b) (F) Se d’ = 2 · d s R’
11. c
R = ρ⋅
17. d


s 1 = 4, 8 ⋅ 10 −7 ⋅
s
π ⋅ (5 ⋅ 10 −4 ) 2
A
4, 8 ⋅ 10 −7 ⋅ 
s1=
s  = 1, 6 m
77, 5 ⋅ 10 −8
12. b
Se observarmos qualquer reta tangente à curva, perceberemos que,
à medida que a corrente elétrica aumenta, a resistência também aumenta, pois a inclinação da reta também aumenta.
13. d
Dobrando o diâmetro, estamos quadruplicando a área da secção
1
transversa. Portanto, R’ =
⋅ R.
4
U
Sendo i = , a corrente fica quadruplicada: i ’ = 4i
R
14. e
ρ⋅L
, temos:
Sendo R =
A
10 − 6 ⋅ L
16 ⋅ L
• R A =
s RA =
Ω
2
π
 5 ⋅ 10 −4 
π⋅

 2 
1, 2 ⋅ 10 − 6 ⋅ L
19, 2 ⋅ L
• R B =
⇒ RB =
Ω
2
π
 5 ⋅ 10 −4 
π⋅

 2 
1, 5 ⋅ 10 −6 ⋅ L
37, 5 ⋅ L
• R C =
⇒ RC =
Ω
2
π
 4 ⋅ 10 −4 
π⋅

 2 
Portanto: RC > RB > RA
i
2
1
⋅R
4
1
⋅ R e i’ = 4 · i
4
d) (V) Se d’ = 2 · d e L’ = 4 · L s R’ = R
e) (F) Se ρ’ ≠ ρ s R’ ≠ R
c) (F) Se d’ = 2 · d s R’ =
18. a
A ddp entre os pontos A e B é praticamente nula.
19. Como cada elétron transfere 8 · 10–19 J, e sendo e = 1,6 · 10–19 C, fazendo
a razão, temos:
8 ⋅ 10 −19
=5V
1, 6 ⋅ 10 −19
20. d
De acordo com os dados: AB > AA. Portanto: RB < RA.
Submetidas a mesma ddp, B será mais brilhante, pois RB < RA.
21. R =
U 224
s R = 224 Ω
=
i
1, 0

s 224 = ρ ·
A
Como R = ρ ·
R’ = ρ ·

π·d2

2
d
π· 
2
(I)
(II)
Dividindo (I) por (II):
ρ·
2
d
π· 
224
224
d2
224
2
=
s
s R’ =
= 56 Ω
=
2
ρ·
4
R'
R'
d
 
2
r · (d )
2
22. U1 = U2 s R1 · i1 = R2 · i2 s
15. e
U

e R= .
A
i
Portanto:
s β · (1 + α · T1) · i1 = β · (1 + α · T2) · i2 s
220
10
= ρ⋅
s ρ = 5,6 · 10–2 Ω · mm2/m
5,5
1, 4 ⋅ 10 −2
s
R = ρ ⋅
De acordo com a tabela: Tungstênio.
Como R = ρ ·

, temos:
A

A1

R2 = ρ2 ·
A2
2R
10ρ 2 A 2
s
2 =
⋅
R2
ρ2
A1
s 2 = 10 ·
25
0, 8
0, 6
s
= 1 + 4 · 10– 3 · T2 s T 2 =
0,5
4 ⋅ 10 −3
s T2 = 150 ºC
Atividades extras
16. d
R1 = 2R2
R1 = ρ1 ·
s (1 + α · 0) · 0,8 = (1 + 4 · 10– 3 · T2) · 0,5 s
A2
A
10
s 1 =
=5
A1
A2
2
23. Soma = 19 (01 + 02 + 16)
(01) (V) De 0 a 600 mA, R é praticamente constante e vale
U
3
=
=5Ω
i
0, 6
R=
Para i = 0,8 A, temos U = 5 V. Nesse ponto:
R=
U
5
=
s R = 6,25 Ω
i
0, 8
(02)(V)
(04)(F)
(08)(F)
(16)(V) R =
ρ 1,5 ⋅ 10 −6 ⋅ 5
=
=5Ω
A
1,5 ⋅ 10 −6
Tarefa Proposta 2
Física
Resolução
(32) (F) Entre 200 mA e 400 mA, a resistência é constante. Nesse
caso, a potência é dada por: P = R · i2
Dobrando-se a intensidade da corrente elétrica, a potência
quadruplica.
24. e
As perdas de energia elétrica por efeito joule são reduzidas quando
se usa um material melhor condutor de eletricidade.
As lâmpadas fluorescentes são mais eficazes que as incandescentes,
para a mesma potência.
FE.06
1.d
A energia elétrica é usada para aquecer a resistência elétrica do
chuveiro (filamento). A energia térmica dissipada pelo filamento
aquece a água.
2.a
2
2
P = U s R = U
P
R
Admitindo que a resistência permaneça constante:
U2 U2
220 2
110 2
=
s
1 = 2 s
5.600
P1 P2
P2
s P2 =
5.600 ⋅ 110 2 5.600
=
s P2 = 1.400 W
220 2
4
3.e
Dt = 60 h
P = 240 W
E
P =
s E = P · Dt s E = 240 · 60 s 14.400 Wh ou
∆t
E = 14,4 kWh
4.e
Consumo do decodificador em 30 dias:
Ed = P · ∆t = 6 · 30 · 24 s Ed = 4.320 W · h
Lâmpada de 60 W:
El = P · ∆t. Sendo El = Ed, temos:
4.230 = 60 · ∆t s ∆t = 72 h
5.a) P = U · i s 60 = 120 · i s i =
b) U = R · i s R =
60
= 0,5 A
120
120
U
= 240 Ω
sR=
0,5
i
6. F – V – F – V – F
P1 = 2.200 W
U1 = 110 V
P2 = 2.200 V
U2 = 220 V
I.(F) As correntes são diferentes em função das tensões que
são diferentes.
U 12
(110) 2
= 5,5 Ω e para
s R1 =
II.(V) Para 1, temos: R 1 =
P1
2.200
2, temos:
R2 =
26
U 22
P2
s R2 =
220 2
= 22 Ω
2.200
Portanto: R2 = 4R1
220
= 10 A
22
III. (F) Em 2, temos: U2 = R2 · i2 s i2 =
IV. (V) Ver itens anteriores.
V. (F) Como as potências são iguais, o consumo é o mesmo.
7.e
Os três fatores são relevantes para o consumo de energia elétrica.
8. U = 18 · 106 V
i = 200 · 103 A
Dt = 1 · 10– 3 s
P = U · i = 18 · 106 · 2 · 105 = 36 · 1011 W = 36 · 108 kW
E = P · Dt
10 −3
= 1.000 kWh
3.600
Fazendo uma regra de três simples, temos:
125 kWh
1 residência
x
1.000 kWh
x = 8 residências
Energia: E = 36 · 108 ·
9.c
P = U · i s 6.000 = 200 · i s i = 30 A
10. b
a) Redução do tempo do chuveiro em 30%:
Economia de 30% · 70 = 21 kWh
b) Substituição das lâmpadas:
2
· 45 = 30 kWh
3
Economia de
c)
d)
e)
Redução do tempo de uso do ferro:
Economia de 50% · 9 = 4,5 kWh
Não usar a máquina de lavar:
Economia de 9 kWh
Redução do tempo de uso da TV:
Economia de 70% · 9 = 6,3 kWh
11. a) O projeto 4 é mais viável, pois tem em uso o fio de menor resistência associado a uma corrente não tão alta, mas suficiente
para gerar a mesma potência que os demais projetos.
b) P = R · i2 = 20 · (0,5)2 = 5 W
Energia: E = 5 · 3.600 = 18.000 J
U
R
Se U for reduzido em 5%, a corrente também será reduzida em
5%, pois são grandezas diretamente proporcionais.
12.a) U = R · i s i =
b) P =
U2
R
Se U for reduzido em 5%, a potência será reduzida em:
P' =
(0, 95U ) 2
s P' = 0, 9025P s P' = 90, 25% de P
R
Sendo assim, houve uma redução de 9,75%, ou seja,
100% – 90,25%.
13. c
Como P = i ∙ U, temos: P = 12 · 200 = 2.400 W
Tarefa Proposta 2
Física
Resolução
14. c
a ligação deles, precisamos conhecer a intensidade de corrente
elétrica.
45
E = P · ∆t s E = 5.000 ·
· 30 s
60
s E = 112.500 Wh = 112,5 kWh
Custo:
R$ 0,20
1 kWh
x
112,5 kWh
s x = R$ 22,50
Atividades extras
22. b
P = 1.000 W = 1 kW
∆t = 15 min =
15. c
A maioria dos equipamentos sofre o efeito Joule, que, evitado, reduz
o consumo de energia elétrica.
16.
d
Chuveiro I: P = U · i s 4.400 = 127 · i s i = 34,6 A
Chuveiro II: P = U · i s 5.400 = 127 · i s i = 42,5 A
Chuveiro III: P = U · i s 5.400 = 220 · i s i = 24,5 A
Chuveiro IV: P = U · i s 6.400 = 220 · i s i = 29,1 A
17. a
A leitura deve ser feita observando-se entre quais números o ponteiro está, levando-se em conta sempre o menor.
A leitura é:
1 – para 1º relógio.
6 – para 2º relógio.
6 – para 3º relógio.
9 – para 4º relógio.
Portanto: 1.669 kWh
18. c
a) Lâmpada de 120 V e 40 W:
2
120 )
Resistência: R = U = (
40
P
2
s R = 360 Ω
b) Lâmpada de 220 V e 40 W:
U 2 ( 220 )
R =
s R = 1.210 Ω
=
P
40
d) A lâmpada queima.
e) A lâmpada queima.
2
19. a
P = 3.600 W = 3,6 kW
1
h · 30 dias = 7,5 h (mês)
4
E = P · Dt = 3,6 · 7,5 = 27 kWh
20.
c
Consumo correspondente aos banhos:
C = 25% · 300 s C = 75 kWh
E = P · ∆t s 75 = 5 · ∆t s ∆t = 15 h
15 h por mês s 0,5 h por dia
Sendo 4 moradores, temos:
E = P · ∆t = 1 · 20 s E = 20 kWh
Preço do kWh =
162,50
= 0,625
260
Acréscimo em reais: 0,625 · 20 s R$ 12,50
23. d
Ferro: P1 = U · i1 s 1.400 = 110 · i1 s i1 = 12,8 A
Micro-ondas: P2 = U · i2 s 920 = 110 · i2 s i2 = 8,4 A
Então, a corrente que passará pelo disjuntor será: i1 + i2, ou seja,
21,2 A. Portanto, o valor mínimo dele, para que não desarme, deverá ser de 25 A.
24. d
I. Aparelhos citados na tabela:
120 + 3.000 + 500 + 2 · 200 + 50 s
s P1 = 4.070 W
II. Lâmpadas na sala: Área = 9 m2 s 100 W
III. Lâmpada no banheiro: Área = 3,1 m2 s 60 W
IV. Lâmpada no corredor: Área = 1,3 m2 s 60 W
V. Lâmpada no quarto: Área = 8,4 m2 s 100 W
P = PI + PII + PIII + PIV + PV s
T
s PT = 4.070 + 100 + 60 + 60 + 100 s
s PT = 4.390 W
FE.07
1.c
Os resistores R1 e R2 estão em curto-circuito.
Portanto: Req. = 0
2.d
P = 0,9 W
U=6V
U2
36
R=
=
= 40 Ω
P 0, 9
Assim, deve-se conectar um resistor em série da mesma magnitude
da resistência da lâmpada para dividir a tensão de 12 V, em 6 V para
cada elemento.
3.d
Resistor equivalente:
Req. = 1 +
3⋅9
s Req. = 3,25 Ω
3+ 9
Corrente total:
0,5 h 30 min
=
⇒ ∆t = 7,5 min/dia
∆t =
4
4
iT =
21. e
A manutenção da temperatura agradável e constante, no interior do
auditório, depende da capacidade de refrigeração dos aparelhos, e,
para se determinar a espessura da fiação do circuito elétrico para
4.b
Chave fechada:
U
iAB =
(I)
R
27
1
1
h s ∆t =
h · 4 · 20 = 20 h
4
4
U
13
=
s iT = 4 A
R eq. 3, 25
Tarefa Proposta 2
Física
Resolução
Chave aberta:
U
i =
(II)
2R
Comparando I com II, temos: iAB = 2 · i
5.c
As lâmpadas estão conectadas em paralelo e, portanto, U60 = U100.
Como P60 < P100, temos R60 > R100, pois P e R são inversamente
proporcionais. Portanto: i60 < i100.
6.e
Em série: Re = 2 · R
P =
U2
U2
s 20 =
s U2= 40 · R
Re
2 ⋅R
10. Soma = 38 (02 + 04 + 32)
Resistor equivalente:
R
Em paralelo: R e =
2
U2
40 ⋅ R ⋅ 2
s P = 80 W
P = R s P =
R
2
7.c
O resistor equivalente da associação é:
R ⋅R
8 ⋅ 12
s Req. = 6 Ω
Req. = R3 + 1 2 s R eq. = 1, 2 +
R1 + R2
8 + 12
A intensidade de corrente no circuito e no resistor R3 vale:
V
24
=
s i = i3 = 4 A
i =
R eq.
6
A voltagem no resistor R3 é:
U3 = R3 · i3 s U3 = 1,2 · 4 s U3 = 4,8 V
A voltagem nos resistores R1 e R2 vale:
U1 = U2 = V – U3
U1 = U2 = 24 – 4,8 s U1 = U2 = 19,2 V
A intensidade de corrente nos resistores R1 e R2 vale, respectivamente:
i 1 =
U 1 19, 2
=
s i1 = 2,4 A
R1
8
i 2 =
U 2 19, 2
=
s i2 = 1,6 A
R2
12
A resistência equivalente do circuito vale:
R1 ⋅ Rv
R1 + Rv
E a intensidade de corrente elétrica no circuito é:
i = U
R eq.
Assim, temos:
a) (F) Para i máximo s Req. deve ser mínima s Rv = 0, ou seja, R1
em curto-circuito.
b) (V) Se Rv = 0 (R1 em curto-circuito) e Req. = R2.
c)(F) iv < i2 = icircuito
d) (F) Se R2 tende a zero, temos: i v =
U
V
e i1 =
Rv
R1
e)(F) U2 = R2 · icirc.. Variando-se Rv, icirc. varia.
28
R e =
R1 ⋅ R2
R1 + R2
+ R3 s Re =
5 ⋅ 20
+6 s Re = 10 Ω
5 + 20
U AB 10
=
s iT = i3 = 1 A
Re
10
U12 = R12 · iT s U12 = 4 · 1 = 4 V
i T =
i 1 =
U 12 4
= s i1 = 0,8 A
R1
5
i 2 =
U 12
4
=
s i2 = 0,2 A
R2
20
2
Ptotal = R e ⋅ i total
= 10 ⋅ (1)2 s Ptotal = 10 W
2
= 6 ⋅ (1)2 s P3 = 6 W
P3 = R 3 ⋅ i total
Assim, temos:
(01)(F)
(02)(V)
(04)(V)
(08)(F)
(16)(F)
(32)(V)
(64)(F)
11. e
Pela primeira lei de Ohm, temos:
U = Req. · i s 6 = Req. · 3 s Req. = 2 Ω é a alternativa correta.
R1 = 4 Ω; R2 = 8 Ω; R3 = 8 Ω
8.b
R1 e Rv estão associados em paralelo:
R ⋅R
R' = 1 v
R1 + Rv
Req. = R2 + R’ s R eq. = R 2 +
9.d
Calculando a ddp no resistor de 2 Ω, temos:
U2 = R2 · i2 s U2 = 2 · 2 = 4 V
Essa é a mesma ddp aplicada ao resistor de 4 Ω (paralelo). Sendo
assim, a corrente no resistor de 4 Ω é dada por:
U2 = R4 · i4 s 4 = 4 · i4 s i4 = 1 A
Portanto, a corrente do circuito é dada por:
itotal = i2 + i4 s itotal = 3 A
Calculando as ddps nos dois resistores que restam, basta somarmos
com U2 e temos a ddp da fonte.
1
U1 = R1 · iT s U1 =
·3=1V
3
Assim, a ddp total é dada por: U = U1 + U2 + U3 = 1 + 4 + 1 = 6 V
U 2 120 2
=
s P = 1.200 W
R
12
b)R1 e R2 estão ligados em paralelo e P1 = 2 · P2. Então:
12.a) P =
U2
U2
= 2⋅
s R2 = 2 · R1.
R1
R2
Sendo R2 + R1 = R0 = 12 Ω, temos:
2 · R1 + R1 = 12 s R1 = 4 Ω e R2 = 8 Ω
c) Na situação II:
R = R 1 ⋅ R 2 s 4 ⋅ 8 = 8 Ω
R1 + R2
4+8 3
Portanto:
U2
R
P
P 12 36
P
= R = 0 s
=
=
s
= 4,5
8
R
8
P0 U 2
P0
P0
3
R0
Tarefa Proposta 2
Física
Resolução
13. d
A resistência equivalente na associação é dada por:
R
3R
R = +R =
eq. 2
2
Assim, para uma ddp de 6 V, temos:
6
4
U = R eq. ⋅ i s i =
⋅2 s i =
3R
R
A ddp entre BC será dada por:
UBC = R ·
4
s UBC = 4 V
R
14. Soma = 7 (01 + 02 + 04)

P 100
 i = U = 120 = 0, 83 A
Lâmpada A: 100 W ~ 120 V s 
2
U 2 ( 120 )

R
=
=
= 144 Ω

P
100

40
P
 i = U = 120 = 0, 33 A
Lâmpada B: 40 W ~ 120 V s 
2
U 2 ( 120 )

R = P = 40 = 360 Ω
RA =
(01)(V)
RB =
ρ⋅A
A
ρ⋅B
A
144 ⋅ A 

ρ 
  = 2, 5 ⋅  A
360 ⋅ A  B
⇒ B =
ρ 
⇒ A =
(02) (V) Em paralelo: UA = UB = 120 V e PA = 100 W e PB = 40 W
Portanto: PA = 2,5 · PB
(04) (V) Como os filamentos não são ôhmicos e a resistividade aumenta com a temperatura, a resistência do filamento é maior
com a lâmpada acesa do que com a lâmpada apagada.
(08) (F) Ligando-se as lâmpadas em série, a intensidade de corrente
elétrica é a mesma para as duas. Como RA < RB, então PA < PB
pois P = R · i2.
(16) (F) Ver cálculo inicial.
15. Com K aberta, temos apenas uma série entre R1 e R2:
Assim: Uxy = (R1 + R2) · i s U2 = 36 · 8 = 288 V
Com a chave fechada:
R eq. = R 1 +
i1 =
U xy
R eq.
=
R2 ⋅ R3
24 ⋅ 8
s R eq. = 12 +
= 18 Ω
R2 + R3
24 + 8
288
s i 1 = 16 A
18
U P = R P ⋅ i 1 = 6 ⋅ 16 s U P = 96 V
U
96
i2 = P =
s i2 = 4 A
R 2 24
16. b
Como o funcionamento das lâmpadas tem de ser independente,
deveremos associá-las em paralelo, e com um interruptor em cada
ramo da associação.
17. U = 120 V
Na série, a corrente é a mesma para ambas, porém brilhará mais
aquela de maior resistência.
Sendo assim:
U2
(120) 2
R 60 =
=
= 240 Ω
P60
60
29
R 100 =
U2
(120) 2
=
= 144 Ω
P100
100
Portanto, como P = R · i2 e i é a mesma para as duas, a lâmpada de
60 W brilhará mais.
18. a)Vazão = 3,0 L/min = 0,05 kg/s
P = Q = U 2 s m ⋅ c ⋅ ∆θ = U 2 s
∆t R 1
∆t
R1
( 200 ) s
2
s 0,05 · 4 · 103 (θf – 20) =
10
s 2 · 102 (θf – 20) = 4 · 103 s
s θf – 20 = 20 s θf = 40 ºC
b) Se a pessoa, em contato com o solo, toca o ponto B, temos:
R1 e R2 em paralelo s R eq. =
s i AB =
R1 ⋅ R2
s
R1 + R2
200
U
=
s iAB = 20,2 A
10 ⋅ 1.000
R eq.
10 + 1.000
19. c
Pela primeira lei de Ohm:
U = Req. · i s 120 = Req. · 50 s Req. = 2,40 Ω
20. Se Req. = R0 temos:
R · (R + R 0 )
Req. = R +
s
R + R + R0
s Req. = R +
R0 =
R 2 + R · R0
2R + R 0
(2R + R 0 ) · R + R 2 + R · R 0
s
2R + R 0
s R0 · (2R + R0) = 2R2 + R · R0 + R2 + R · R0 s
s 2R · R0 + R02 = 3R2 + 2R · R0 s R02 = 3R2 s
s R 0 = 3 ⋅ R s R =
s R H 10 Ω
3
1, 73
⋅ R0 s R =
⋅ 17, 3 s
3
3
21.a) Em R3 , temos: U3 = R3 · i3
U3 = 16 · 2 = 32 V
Essa tensão é a mesma em R2.
Então:
U2 = U3 = R2 · i2 s 32 = 4 · i2 s i2 = 8 A
Assim i1 = (8 + 2) = 10 A
b)Em R1, temos:
U1 = R1 · i1 s U1 = 6,8 · 10 s
s U1 = 68 V
Portanto: UAC = (68 + 32) = 100 V
22. d
Teremos o maior consumo na associação em que as lâmpadas estiverem funcionando em acordo com seus dados nominais.
Atividades extras
23.a) R1 = (10 · 100 ± 5%) Ω; R2 = (3 · 101 ± 10%) Ω
Portanto: R1 = (10 ± 5%) Ω e R2 = (30 ± 10%) Ω
Tarefa Proposta 2
Física
Resolução
b)
(01) (F) As lâmpadas brilham iguais, pois possuem a mesma resistência.
(02)(V) RA = RB e a corrente é a mesma.
(04)(F) RA = RB e UA = UB
(08)(V) RA = RB e iA < iB
(16) (F) a lâmpada B apaga, pois fica em curto-circuito.
R’
R2
R1
R1
R2
A
2.a) Se i = 0,1 A, temos:
U = Req. · i s
s 1,5 = (2R + R) · 0,1 s 3R =
B
R’ = R1 + R2 = 10 + 30 s R’ = 40 Ω
sR=5Ω
No resistor R, temos:
UR = R · i = 5 · 0,1 s
s UR = 0,5 V
b)
R’’
R’
1,5
s
0, 1
R1
3.d
A lâmpada, em perfeito funcionamento, é percorrida por uma corrente elétrica igual a:
P = U · i s 12 = 6 · i s i = 2 A
No circuito, temos:
ε = UAB + Ulâmp. s 9 = UAB + 6 s UAB = 3 V
A resistência de um resistor ôhmico ligado entre A e B vale:
R2
A
B
1
1 1
1
1
=
+
= +
s R” = 8,0 Ω
R ” R ’ R 1 40 10
U AB 3
= s R = 1,5 Ω
i
2
Assim:
a) (F) Veja os cálculos.
b)(F)
c)(F) A ddp entre A e B é 3 V.
d)(V)
e)(F)
R =
Req.
R’’
R2
A
B
4. a) Remontando o circuito, temos:
Req. = R” + R2 = 8 + 30 s Req. = 38 Ω
c) i total
A
U
76
= AB =
s itotal = 2 A
R eq. 38
(L1)
i
E
+
–
i4
(L3)
R
R
i7
i6
(L5)
R
(L6)
R
E
R
(L7)
R
(L8)
D
A
R ED =
D
D
2R
=R
2
30 Ω
G
G
1
1
1
1
1
5 + 2 + 1+ 2
=
+
+
+
=
R eq. 12 30 60 10 + 20
60
s R eq. = 60 = 6 Ω
10
b)UCD = 10 V
UCD = RCD · i1 s 10 = 20 · i1 s i1 = 0,5 A
UAD = RAD · i s RAC · i1 = 30 · 0,5 = 15 V
Assim: UAD = UAG
Portanto: UAG = Req. · i s 15 = 6 · i s i = 2,5 A
c) U = ε – r · i s 15 = ε – 2 · 2,5 s ε = 20 V
d) P = r · i2 s
s P = 2 · (2,5)2 = 2 · 6,25 = 12,5 W
5. U = 12 V
E = 6 · 103 Wh
P = 6.000 W
P = U · i s 6.000 = 12 · i s i = 500 A
FE.08
i =
30
G
A Req. entre A e G é dada por:
RCD = R + R = 2 ⋅ R
Portanto: i2 = i4
As lâmpadas L2, L3 e L4 terão o mesmo brilho, pois i2 = i3 = i4.
1.Soma = 10 (02 + 08)
60 Ω
C
(L4)
R
A=B
C
20 Ω
G
R
i
i2
(L2)
A
10 Ω
12 Ω
r=2Ω
i
C
A
ε
24. b
i2 = i3 (série); i5 = i6 (série) e i7 = i8 (série)
i1 = i2 + i4 e i4 = i5 + i7
B
A
Q
s Q = 500 · 3.600 = 18 · 105 C
∆t
G=D
s
Tarefa Proposta 2
Física
Resolução
6.a
A intensidade de corrente elétrica, na lâmpada (e no circuito), vale:
P = U · i s 60 = 120 · i s i = 0,5 A
Como se trata de um circuito no qual a lâmpada e a solução aquosa
estão associadas em série, temos:
ε = Ulâmpada + Usolução s 127 = 120 + Usolução. s Usolução = 7 V
Portanto, a resistência elétrica da solução vale:
Usolução = R · i s 7 = R · 0,5 s R = 14 Ω
7.d
ε = 60 V
R=1Ω
a) Calculando a Req., temos:
1
1 1 1 3+ 2+1
= + + =
s
R AB 2 3 6
6
i=
R
60
s i=
=4A
r + R eq.
1 + 14
b) A corrente que passa pelo conjunto entre A e B é a metade do
total s iIB = 2 A.
Sendo assim: UAB = RAB · iAB s UAB = 1 · 2 = 2 V
8.c
Fechando-se S, diminui-se a Req. do circuito e, portanto, aumenta-se
a corrente total que passa por R3.
9.a) L1 e L2 em paralelo: U1 = U2. Portanto:
R1 · i1 = R2 · i2 s 10 · 1 = 40 · i2 s i2 = 0,25 A
b)U1 = R1 · i1 = 10 · 1 s U1 = 10 V. Assim:
U = ε – R(i1 + i2) s 10 = 100 – R(1 + 0,25) s
s 1,25 · R = 90 s R = 72 Ω
c) O fusível queima para valores de R menores que X.
A corrente no fusível é dada por:
i f =
100
Quanto menor R, maior ifusível.
( 10 + 1, 25 ⋅ R )
Portanto, o fusível queima para valores de R menores que X.
10. e
I.(F) A corrente tem sentido anti-horário.
II.(V) ε2 é gerador e ε1 é receptor.
III.(V) i =
ε2 − ε1
24 − 6
=
6⋅3
R eq.
+ 4 + 1+ 2
6+3
IV. (F) UAB = RAB · i =
=2A
6⋅3
· 2 s UAB = 4 V
6+3
11. Fechando-se a chave A (contato elétrico), temos o circuito:
C
R
R
6V
31
UCD = RCD · i =
R 4
⋅ s UCD = 2 V
2 R
12. a
Curva característica de um gerador.
U = ε – r · i s 8 = 12 – r · 2 s r = 2 Ω
P =
U2
( 20 )
s 40 =
R
R1
2
s R1 = 10 Ω
A intensidade da corrente na lâmpada L1 vale:
i =
20
ε
=
s i = 0,4 A
R eq. 30 + 10 + 10
E a potência dissipada por ela vale:
P1 = R · i2 = 10 · (0,4)2 s P1 = 1,6 W
b)Fio F conectado no ponto B: a lâmpada L1 fica em curto-circuito.
∴ P1 = 0
P2 =
U2
R2
=
20 2
= 40 W
10
Sendo R2 = R1 = 10 Ω (as lâmpadas são iguais), a potência da
lâmpada L2 é 40 W, pois a ddp em seus terminais é 20 V.
14. a
Calculando Req., temos:
Req. = R1 +
R2 ⋅ R3
s Req. = 30 + 15 = 45 Ω
R2 + R3
U = Req. · i s 36 = 45 · i s
s i = 0,8 A
Para R1, temos:
U1 = 30 · 0,8 = 24 V
Para R2 e R3, temos:
U2 = U3 = 36 – 24 s
s U2 = U3 = 12 V
15. d
I.(F) A indicação é da potência (energia/tempo).
II.(V) P = 1.800 ·
III. (F) Veja afirmativa I.
4
s P = 120 W
60
16. V – V – F – V – F
6⋅3
s Req. = 4 Ω
6+3
I.(V) Req. = 2 +
II.(V) i =
III.(F) UCB = Rp · i =
IV.(V) P = R · i2 = 2 · (4)2 s P = 32 W
V.(F) P = U · i = (ε – r ⋅ i) · i s
s P = (20 – 1 · 4) · 4 s P = 64 W
D
R
ε
ε
6
4
=
=
s i=
R eq. R + R
1,5 ⋅ R R
2
13. a)Fio F conectado no ponto A: a lâmpada L2 fica em curto-circuito.
Portanto: P = 0.
A resistência da lâmpada L1 vale:
s RAB = 1 Ω
No paralelo de 10 Ω, com RAB + 9, temos:
10
=5Ω
R eq. 1 =
2
Req. = Req.1 + 5 + 4 = 14 Ω
Calculando i para o circuito, temos:
i =
20
ε
s i=4A
=
r + R eq. 1 + 4
6⋅3
· 4 s UCB = 8 V
6+3
Tarefa Proposta 2
Física
Resolução
17. a) Remontando o circuito, temos:
A
i =
K
AK
s 8 + 25 + 5R = 48 s 5R = 15 s R = 3 Ω
ε = 12 V
r=0
12 Ω
12 Ω
12 Ω
BJ
B
B
J
12
=4Ω
3
A corrente total no circuito é dada por:
U = Req. · i s 12 = 4 · 1 s i = 3 A
b) No ramo AK, temos a corrente que passa pelo 1º ramo do circuito:
U = R1 · iAK s 12 = 12 · iAK s i = 1 A
No ramo BJ, temos a corrente que vem de um paralelo de dois
resistores e que será somada à corrente de AK, finalizando a
corrente total do circuito:
12 = 6 · iBJ s iBJ = 2 A
Assim: Req. =
18. a) Sendo 1 ano = 8.760 h, a energia gerada, por m2, é dada por:
E = 0,2 · P · ∆t = 0,2 · 170 · 8.760 s E = 297.840 Wh
E a área horizontal vale:
1m 
 A = 3 ⋅ 10 8 m 2 = 300 km 2
A 
297.840 Wh
b)71,4%
E
87.600 GWh
Pf =
=
s Pf = 10 GW
∆t
8.760 h
Pf
Pinst.
=
21. a) Com o interruptor desligado, a ddp nos extremos do chuveiro
(pontos 1 e 2) é zero, pois o chuveiro não está em funcionamento.
b) Com o interruptor desligado, o ponto 3 é um ponto do neutro e
o ponto 4, da fase. Assim, a ddp entre 3 e 4 é 220 V.
c) No verão, sim; no inverno, não.
No verão: P = 2.200 W e U = 220 V. Assim:
P 2.200
=
s i = 10 A.
U
220
Como o disjuntor é de 15 A, ele suporta a carga do chuveiro.
No inverno: i =
i =
P 4.400
=
= 20 A
U
220
O disjuntor não suporta a carga.
22. c
Eficiência =
E visível ( 0, 4 − 0, 8 )
=
E total
( 0, 4 − 2, 0 )
Eficiência =
0, 4
= 0,25 s ef. = 25%
1, 6
2
87.600 ⋅ 10 9 Wh
n =
48
ε
s 5 · (1,6 + 5 + R) = 48 s
s5=


16
R eq.
 + 5 + R

 10
10 ⋅ 10 9 = 0,714 ou 71,4%
14 ⋅ 10 9
Atividades extras
23. e
Na tabela, os sistemas que apresentam menor eficiência são as
lâmpadas incandescentes e a célula solar. Nesses sistemas, ocorrem
transformações de energia radiante em energia elétrica.
24. Com a pilha invertida, temos o seguinte circuito:
2
Ω
3
19. a
Se o poder calorífico é de 3 · 107 J/kg, para 900 g = 0,9 kg, a energia
será:
E = 3 · 107 J/kg · 0,9 kg = 2,7 · 107 J
P=
Assim: n =
PT
= 3.000 s n = 0,4 ou n = 40%
7.500
20. e
No resistor de 8 Ω, temos: U = 8 · 1 = 8 V, que é a mesma tensão
para o resistor de 2 Ω. Então:
8 = 2 · i2 s i2 = 4 A. Dessa forma, a corrente total que percorre o
circuito é de:
i = (1 + 4) = 5 A
Assim:
32
1,5 V
2
Ω
3
i
i
E
2, 7 ⋅ 10 7
sP=
= 7.500 W
∆t
3.600
Pu
2
Ω
3
1,5 V
i
3 Ω
1,5 − 1,5 + 1,5
= 0, 3 A
5
b)Pd = R · i2 = 3 · (0,3)2 = 0,27 W
c) Se a pilha tivesse sido ligada corretamente:
a) i =
4,5
s i0 = 0,9 A
5
P0 = R · i02 s P0 = 3 · (0,9)2 = 2,43 W
i 0 =
∴ Razão
1
P 0, 27
P
=
= 0, 11 ou
=
P0 2, 43
P0 9
1,5 V
i
Tarefa Proposta 2
Física
Resolução