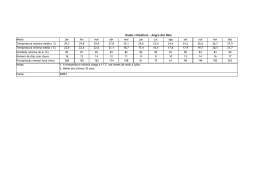
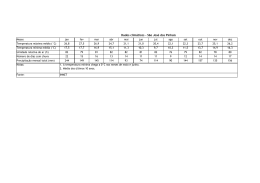
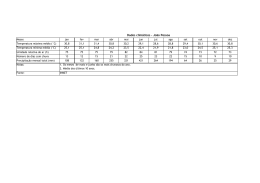
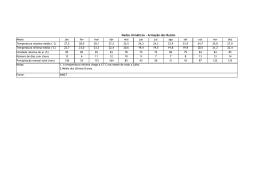
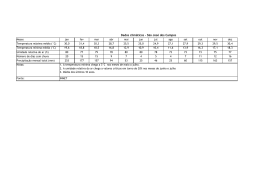
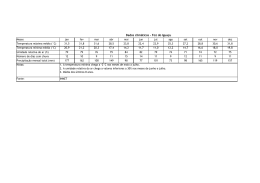
A REPRESENTATIVIDADE DO VALOR MÉDIO EM AMOSTRAS COM GRANDES AMPLITUDES
Francisco de Assis Salviano de Sousa, DCA/CCT/UFPb, e-mail: [email protected]
Josiclêda Domiciano Galvíncio, CPGM/CCT/UFPb, e-mail: [email protected]
ABSTRACT
In this study the law of basic probability and the arithmetic mean of ten time series of total monthly precipitation
(TMP) at stations selected from five regions in Paraíba State are used to calculate the probablity of occurrence of
TMP above or below the mean value.In three of the five regions studied the arithmetic mean is a good indicator of
the distribution of TMP’s in all the years. In the “Sertão” the mean value is not a good measure during the period
August—October. In the “Cariri” region the mean is not a representative measure of TMP’s during the dry months:
September, October and November. The results of the study suggest that such mean values should be used with
caution in models of climate forecasting.
RESUMO
Neste trabalho utiliza-se a lei de probabilidade básica, o valor numérico da média aritmética de dez séries
temporais — totais mensais precipitados (TMP’s) — de postos situados em cinco diferentes regiões do Estado da
Paraíba, com diferentes tamanhos amostrais (N), para calcular a probabilidade de ocorrer TMP’s abaixo ou acima
desse valor numérico e evidenciar a representatividade do valor médio amostral.
Em três das cinco regiões estudadas, a média flutua em torno de 60 por cento dos TMP’s. Isso evidencia
uma ótima representatividade dessa estatística e uma boa distribuição dos TMP’s em todos os anos. Na região do
Sertão a média não é representativa para os meses secos: agosto, setembro e outubro. Neles, aproximadamente, 80
por cento dos TMP’s estão abaixo do valor numérico da média e na região do Cariri a média não é representativa
para os meses secos: setembro, outubro e novembro. A não representatividade da média nesses meses evidencia má
distribuição dos TMP’s. Portanto, recomenda-se cautela quando se fizer uso dessas médias em modelos de previsão
climática, principalmente se elas forem um dos parâmetros desses modelos.
INTRODUÇÃO
A importância da representatividade do valor numérico da média aritmética ou momento de ordem um
pode ser ressaltada nos modelos estatísticos de previsão como, por exemplo, Thomas-Fiering, Autoregressivos
(AR), Médias Móveis (MA), Análise Harmônica, dentre outros que utilizam a média aritmética como origem dos
desvios (anomalias) dos valores observados.
A representatividade do valor médio pode ser evidenciada também no ajuste dos dados a qualquer função
distribuição de probabilidade paramétrica ou modelo probabilístico. Dessas funções, as mais utilizadas na
meteorologia e climatologia são: Normal, Log-Normal, Gumbel, Weibull, Gamma, Beta, Bernoulli, Poisson e
Exponencial. Essa representatividade tem igual importância nos momentos de ordem dois (variância), três e quatro,
visto que esses momentos compõem os coeficientes de assimetria, curtose e de variação, responsáveis pelas
principais características de uma amostra.
Na meteorologia, até o momento, pouco se sabe, quantitativamente, à respeito do processo gerador da
precipitação. Muitas vezes o conhecimento adquirido: o qualitativo, é isolado da influência das inter-relações das
variáveis meteorológicas. Nesse contexto a incerteza quanto a representatividade do valor numérico da média
aritmética é mais um complicador nos resultados da previsão climática elaborada por modelos estatísticos ou
dinâmicos.
Os primeiros relacionam as previsões, quanto ao ano ou mês ser seco, normal ou chuvoso, com base nos
valores das médias aritméticas climatológicas e utilizam esses valores como parâmetros, portanto, na prática, é um
valor limitador nesses modelos. Já nos modelos dinâmicos, o valor da média pode não ser um parâmetro, mas os
resultados das previsões têm como referência esse valor, que também limita as previsões.
Toda essa teoria acerca da representatividade do valor numérico da média aritmética, considera os dados
observados não-agrupados. Caso se agrupe, a falta de representatividade poderá aumentar, principalmente se os
dados apresentarem grande dispersão. Esse é um caso típico de uma amostra de totais mensais precipitados no
546
Semi-Árido nordestino, visto que pode-se dispor em uma mesma amostra valores extremos, observados em
períodos secos e chuvosos.
A média aritmética é comumente utilizada, por exemplo, em meteorologia e climatologia para representar
o a valor central ou esperado de uma variável qualquer em um ponto fixo no espaço e no tempo. Quando os valores
observados de séries anuais longas tendem para um valor central, diz-se que esse último valor é “real” e é
denominado “normal climatológico”. Por existir vários tipos de médias, doravante, neste trabalho, a palavra média
terá o significado de média aritmética. Em geral, segundo BROOKS; CARRUTHERS (1978), a média aritmética
oferece maiores vantagens do que a mediana, são elas:
i)
ii)
iii)
a média é um padrão mais conveniente para referenciar as flutuações de uma variável, visto que no
intervalo representado pela média a soma dos desvios é igual a zero. Por esta razão apenas ela é um nível
de referência praticável, para os desvios acumulados, na exibição da tendência da série;
para uma dada série de valores observados, o valor médio é mais rapidamente calculado do que a mediana;
as médias para diferentes períodos são prontamente combinadas, enquanto as medianas não são; a média é
mais estável do que a mediana, e o erro padrão da estimativa para uma amostra de observações é menor;
Por outro lado, quando a distribuição é anormal a média geralmente não é uma estatística representativa.
Por exemplo, em climas semi-áridos a precipitação média, para um dado mês, poderá ser maior do que o quartil
superior, isto é ocorrer menos do que um mês em quatro.
A mediana tem as seguintes vantagens:
i)
ii)
é quase sempre representativa e geralmente dá uma estimativa melhor do valor esperado do que a média,
visto que metade das observações estão de um lado e a outra metade do outro lado da mediana. Exceção
ocorre quando mais da metade das observações estão em uma classe extrema, por exemplo, mais do que a
metade dos meses são secos (ou seja, sem ocorrência de chuva). Nesses casos as estatísticas média e
mediana não são representativas;
exceto para dados com distribuições aproximadamente normais, a mediana juntamente com os quartis dão
maior representatividade à distribuição desses dados do que a média e o desvio padrão.
METODOLOGIA
Para estudar a representatividade do valor numérico da média aritmética foram utilizadas dez séries
temporais, de totais mensais precipitados (TMP’s), com diferentes tamanhos amostrais (N), de postos situados em
cinco diferentes regiões do Estado da Paraíba. No Litoral, João Pessoa e Alhandra; no Brejo, Areia e Bananeiras;
no Agreste, Campina Grande; no Cariri, Bodocongó, Soledade e Cabaceiras e no Sertão, Sousa e Patos.
Utilizando-se da lei de probabilidade básica e do valor numérico da média de cada uma das séries
supracitadas, efetuou-se o cálculo da probabilidade de ocorrer totais mensais precipitados (TMP’s) abaixo ou acima
desse valor numérico. Aqui o valor numérico de cada uma das médias é considerado como a Normal Climatológica
(NC).
RESULTADOS E DISCUSSÃO
Tabela 1 – Valores médios mensais da precipitação em milímetros (P), probabilidade de ocorrer TMP’s menor ou
igual a NC (P≤P), maior que a NC (P>P) e tamanho da amostra em anos (N)
Região: Agreste
P
P≤ P
P>P
N
jan
38,0
63,5
36,5
74
Posto: Campina Grande
fev
55,0
62,1
37,9
74
mar
97,0
55,4
44,6
74
abr
111,0
56,7
43,3
74
mai
109,0
52,7
47,3
74
jun
110,0
59,4
40,6
74
547
jul
107,0
55,4
44,6
74
ago
58,0
58,1
41,9
74
set
28,0
62,1
37,9
74
out
12,0
66,2
33,8
74
nov
13,0
61,6
38,4
74
dez
20,0
63,5
36,5
74
Tabela 2 – Valores médios mensais da precipitação em milímetros (P), probabilidade de ocorrer TMP’s menor ou
igual a NC (P≤P), maior que a NC (P>P) e tamanho da amostra em anos (N)
Região: Litoral
Posto: João Pessoa
P
P≤ P
P>P
N
jan
80,0
60,6
39,4
66
fev
101,0
62,6
37,4
67
mar
205,0
56,2
43,8
64
abr
264,0
56,2
43,8
64
mai
jun
283,0 302,0
54,8
60,3
45,2
39,7
62
63
jul
237,0
61,2
38,8
67
ago
140,0
50,7
49,3
67
set
68,0
62,1
37,9
66
P
P≤ P
P>P
N
70,0
60,7
39,3
56
108,0
53,5
46,5
56
199,0
58,9
41,1
56
226,0
56,6
43,4
53
288,0
56,1
43,9
57
273,0
59,2
40,8
49
149,0
62,2
37,8
53
75,0
63,1
36,9
57
296,0
55,5
44,5
54
out
nov
28,0
28,0
64,7
65,7
35,3
34,3
68
67
Posto: Alhandra
38,0
41,0
54,4
67,3
45,6
32,7
57
55
dez
36,0
69,7
30,3
66
50,0
64,3
35,7
56
Tabela 3 – Valores médios mensais da precipitação em milímetros (P), probabilidade de ocorrer TMP’s menor ou
igual a NC (P≤P), maior que a NC (P>P) e tamanho da amostra em anos (N)
Região: Brejo
Posto: Areia
P
P≤ P
P>P
N
jan
67,0
57,1
42,9
77
fev
94,0
54,5
45,5
77
mar
161,0
55,8
44,2
77
abr
174,0
51,3
48,7
76
mai
178,0
57,3
42,7
75
jun
204,0
59,2
40,8
76
jul
193,0
59,2
40,8
76
ago
132,0
55,2
44,8
76
set
65,0
58,6
41,4
75
out
32,0
68,9
31,1
74
P
P≤ P
P>P
N
61,0
65,3
34,7
54
88,0
58,7
41,3
55
154,0
48,1
51,9
57
171,0
57
43
54
164,0
57
43
54
168,0
59
41
63
149,0
50,6
49,4
56
100,0
57,3
42,7
53
52,0
60
40
57
19,0
60
40
56
nov
dez
31,0
42,0
67,5
61,3
32,5
38,7
74
75
Posto: Bananeiras
23,0
33,0
68
62,8
32
37,2
61
63
Tabela 4 – Valores médios mensais da precipitação em milímetros (P), probabilidade de ocorrer TMP’s menor ou
igual a NC (P≤P), maior que a NC (P>P) e tamanho da amostra em anos (N)
Região: Sertão
Posto: Patos
P
P≤ P
P>P
N
jan
66,0
62,6
37,4
73
fev
133,0
58,2
41,8
73
mar
207,0
52,2
47,8
69
abr
155,0
56,3
43,7
75
mai
60,0
60,5
39,5
75
jun
22,0
69,8
30,2
74
jul
9,0
68
32
71
ago
3,0
78,6
21,4
72
set
1,0
84
16
75
out
6,0
79,7
20,3
71
P
P≤ P
P>P
N
89,0
61,6
38,4
73
153,0
49,3
50,7
73
219,0
50,7
49,3
73
157,0
60,8
39,2
74
72,0
58,6
41,4
75
29,0
59,1
40,9
71
12,0
59,1
40,9
71
4,0
80
20
70
4,0
82,4
17,6
74
6,0
71,6
28,4
74
548
nov
dez
15,0
26,0
78,3
67,5
21,7
32,5
73
68
Posto: Sousa
13,0
33,0
77,5
68,5
22,5
31,5
71
73
Tabela 5 – Valores médios mensais da precipitação em milímetros (P), probabilidade de ocorrer TMP’s menor ou
igual a NC (P≤P), maior que a NC (P>P) e tamanho da amostra em anos (N)
Região: Cariri
Posto: Bodocongó
P
P≤ P
P>P
N
jan
16,0
63,1
36,9
57
fev
37,0
65
35
57
mar
80,0
60
40
55
abr
79,0
59
41
56
mai
53,0
62,6
37,4
56
jun
54,0
57
43
58
jul
48,0
50
50
58
ago
19,0
65
35
57
set
8,0
67,2
32,8
58
out
6,0
77,6
22,4
58
P
P≤ P
P>P
N
23,1
66,2
33,8
80
54,6
65
35
80
99,7
58,7
41,3
79
87,9
67,5
32,5
79
38,3
60,2
39,8
78
32,9
65,4
34,6
78
28,4
59,7
40,3
77
8,4
64,9
35,1
77
2,8
76
24
79
5,4
88,6
11,4
79
P
P≤ P
P>P
N
15,4
54,4
45,6
79
36,5
62,3
37,7
77
49,3
65,7
34,3
73
62,9
60,2
39,8
73
38,9
60
40
75
37,3
60
40
75
35,4
59,7
40,3
77
12,2
64,5
35,5
79
3,4
73,4
26,6
79
3,0
87,3
12,7
79
nov
dez
5,0
10,0
70,7
65,5
29,3
34,5
58
58
Posto: Soledade
3,4
10,8
82,3
74,7
17,7
25,3
79
79
Posto: Cabaceiras
3,0
6,8
72,7
77,9
27,3
22,1
77
77
Na prática é raro encontrar uma amostra de um evento meteorológico que tenha o valor numérico da média
aritmética posicionado exatamente em 50 por cento do total de casos. Comumente esse valor encontra-se entre 45 e
65 por cento do total de casos.
A Figura 1 resume os resultados das cinco regiões estudadas (Tabelas 1 a 5). Nota-se nas Figura 1(a, b, c)
que a média flutua em torno de 60 por cento dos TMP’s . Isso evidencia uma ótima representatividade dessa
estatística e uma boa distribuição dos TMP’s em todos os anos.
Na região do Sertão (Figura 1d) a média não é representativa para os meses secos: agosto, setembro e
outubro. Neles, aproximadamente, 80 por cento dos TMP’s estão abaixo do valor numérico da média e na região do
Cariri (Figura 1e) a média não é representativa para os meses secos: setembro, outubro e novembro. A não
representatividade da média nesses meses evidencia má distribuição dos TMP’s. Portanto recomenda-se cautela
quando se fizer uso dessas médias em modelos de previsão climática, principalmente se elas forem parâmetros
desses modelos.
Agreste
80
60
50
40
30
20
10
Campina Grande
Percntual
Percentual
70
Litoral
60
40
João Pessoa
Alhandra
20
0
0
jan fev mar abr mai jun jul ago set out nov dez
jan fev mar abr mai jun jul ago set out nov dez
(a)
(b)
549
100
Areia
Bananeiras
Percentual
Percentual
Sertão
Brejo
80
70
60
50
40
30
20
10
0
80
60
40
Patos
20
Sousa
0
jan fev mar abr mai jun jul ago set out nov dez
jan fev mar abr mai jun jul ago set out nov dez
(c)
(d)
Cariri
Percentual
100
80
60
40
Bodocongó
Soledade
Cabaceiras
20
0
jan fev mar abr mai jun jul ago set out nov dez
(e)
Figura 1- Probabilidade percentual para ocorrência de totais mensais precipitados – TMP’s menores ou iguais a
média aritmética
CONCLUSÃO
Para os meses mais secos das regiões tipicamente semi-áridas, cariri e sertão, a média aritmética não é uma
estatística representativa dos totais mensais precipitados—TMP’s.
REFERÊNCIAS BIBLIOGRÁFICAS
BROOKS, C.E.P. ; CARRUTHERS, N. Handbook of Statistical Methods in Meteorology. London, Her Magesty’s
Stationary Office, 412p., 1978.
550