ALUNO(a):
___________________________________________
Nº: ____
SÉRIE: 1º
UNIDADE:
VV 
Valor:
TURMA:_____
JC 
JP 
PC 
5,0
DATA: ___/___/2014
Obs.: Esta lista deve ser entregue apenas ao professor no dia da aula de Recuperação
SETOR A
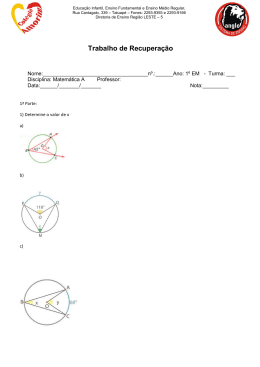
1. Se A
x
* | 2
x
4 e B
x
* | 2
x
4 , determine:
a)
A B
c)
B A
b)
A B
d)
CAB
2. Feita uma pesquisa sobre as revistas que os estudantes leem mais, tivemos o seguinte resultado:
A
44%
B
40%
AeB
24%
Responda:
a) Quantos por cento leem apenas a revista A?
b) Quantos por cento leem apenas a revista B?
2013_Matemática_1° ano_1º tri
c) Quantos por cento não leem nenhuma das duas revistas?
3. Uma cidade é servida por duas empresas de telefonia. A empresa x cobra, por mês, uma assinatura de
R$35,00, mais R$ 0,50 por minuto utilizado. A empresa y cobra, por mês, uma assinatura de R$ 26,00,
mais R$0,65 por minuto utilizado. A partir de quantos minutos de utilização o plano da empresa x passa
ser mais vantajoso para os clientes do que o plano da empresa y?
1
4. Se f(x) =x² + 4x - 6, determine o valor de 3f(-2) + 4f(-3).
5. Considere os conjuntos A = {-2, -1, 0, 1} e B = { -3, -2, -1}, determine:
a) os pares ordenados da relação R
x,y
A B| y
x3
2 .
b) A
B
b) o domínio e o conjunto imagem de R.
6. Seja A = ] 6, 9] e B = [7, 10[ , determine:
a) A B
7. Analisando as carteiras de vacinação das 84 crianças de uma creche, verificou-se que 68 receberam a
vacina Sabin; 50 receberam a vacina contra Sarampo e 12 não foram vacinadas. Quantas dessas
crianças receberam as duas vacinas?
8. Quantos números inteiros e positivos satisfazem a inequação
a) nenhum
b) 1
9. Considerando a função f de
que f(x) = 0.
c) 2
d) 3
x
2
2x 7
3
0?
e) 4
 em  , definida por f(x) = x² - 5x + 6 , calcule o valor numérico de x, tal
2
R definida por f(x) = x³ - x + 10. Determine o valor numérico de f para
cada elemento de seu domínio D ={ -2, -1, 0, 1}, ou seja determine o conjunto imagem de f .
10. Considerando a função
f :D
SETOR B
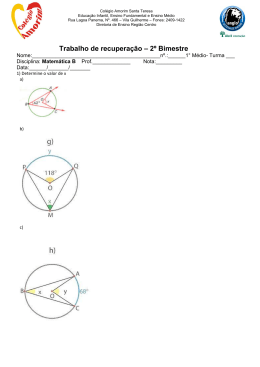
1. Se a soma das medidas dos arcos APB e CQD é 160°, então o ângulo
a) 60°
b) 65°
c) 70°
d) 75°
mede
e) 80º
2. Considere a figura abaixo. A medida x do ângulo assinalado é
a) 90º
b) 85º
c) 80º
d) 75º
e) 70º
3. Na figura seguinte, A e B são os centros das duas circunferências. O valor do ângulo
4. Exprima, em radianos, as medidas dos x e y tais que x + y = 70° e x - y = 50º.
5. Quanto mede, em radianos, um arco de 3°?
3
é
6. Um avião levanta voo sob um ângulo de 30°. Então, depois que tiver
percorrido 500 m, conforme indicado na figura, sua altura h em relação ao
solo, em metros, será igual a:
7. Duas pessoas A e B estão situadas na mesma margem de um rio
distantes 60 3 m uma da outra. Uma terceira pessoa C, na outra
margem do rio, está situada de tal modo que AB seja perpendicular a
AC e a medida do ângulo ACB seja 60°. A largura do rio é
8. Um barco parte de A para atravessar o rio. A direção de seu
deslocamento forma um ângulo de 120° com a margem do rio. Sendo a
largura do rio 60 m, a distância, em metros, percorrida pelo barco foi de
9. A prefeitura de certa cidade vai construir, sobre um rio que corta essa cidade,
uma ponte que deve ser reta e ligar dois pontos, A e B, localizados nas margens
opostas do rio. Para medir a distância entre esses pontos, um topógrafo
localizou um terceiro ponto, C, distante 200 m do ponto A e na mesma margem
do rio onde se encontra o ponto A. Usando um teodolito (instrumento de
precisão para medir ângulos horizontais e ângulos verticais muito empregados
em trabalhos topográficos), o topógrafo observou que os ângulos B Ĉ A e C Â B
mediam, respectivamente, 30º e 105º, conforme ilustrado na figura a seguir.
Com base nessas informações, é correto afirmar que a distância, em metros, do
ponto A ao ponto B é de:
10. Um triângulo ABC tem lados AB e BC que medem, respectivamente, 5 cm e 7 cm. Determine a medida
do lado AC, sabendo que o ângulo B mede 60º.
11. Um triângulo ABC tem lados AB e BC que medem, respectivamente, 6 cm e 8 cm. Determine a medida
do lado AC, sabendo que o ângulo B mede 120º.
4