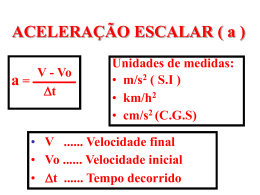
Física  MECÂNICA
DISCIPLINA:
ASSUNTO:
PROF.
Sílvio
MOVIMENTO UNIFORME
02
ALUNO:
SENO
SÉRIE:
UNIDADE(S):
(*)
MOVIMENTO UNIFORME


 m
s
 
= 3,6
()
SUL
18/08/2015
ATIVIDADES
CARACTERÍSTICAS
OBS  1
U
TURMA(S)
CENTRO
LISTA
Nº:
01) Um trem sai da estação de uma cidade, em percurso
retilíneo, com velocidade constante de 50 km/h. Quanto
tempo depois de sua partida deverá sair, da mesma estação,
um segundo trem com velocidade constante de 75 km/h para
alcançá-lo a 120 km da cidade?
a) 24 min;
b) 48 min;
c) 96 min;
d) 144 min;
e) 288 min.
 km 
 h 
 
02) Dois móveis, A e B, percorrem uma mesma trajetória
retilínea, conforme as funções horárias:
FUNÇÃO HORÁRIA:
SA = 50 + 20 t e SB = 90 – 10 t,
Movimento Progressivo
Movimento Regressivo
V>0

V<0
sendo a posição s em metros e o tempo t em segundos. No
instante t = 0, a distância entre os móveis era de:
a) 30 m
b) 40 m
c) 50 m
d) 90 m
e) 140 m
03) Dois barcos partem simultaneamente de um mesmo
ponto, seguindo rumos perpendiculares entre si. Sendo de 30
km/h e 40 km/h suas velocidades constantes, a distância
entre os barcos, após 6 min, vale:
a) 7 km
b) 1 km
c) 300 km
d) 5 km
e) 420 km
GRÁFICOS DO MOVIMENTO UNIFORME
04) Uma martelada é dada na extremidade de um trilho. Na
outra extremidade encontra-se uma pessoa que ouve dois
sons, separados por um intervalo de tempo de 0,18 s. O
primeiro som se propaga através do trilho, com velocidade de
3.400 m/s, e o segundo através do ar, com velocidade de
340 m/s. O comprimento do trilho vale:
a) 18 m
b) 34 m
c) 36 m
d) 56 m
e) 68 m

ENCONTRO E ULTRAPASSAGEM DE MÓVEIS
SA = SB

VELOCIDADE RELATIVA
MESMO SENTIDO
SENTIDOS OPOSTOS
05) Dois móveis, A e B, descrevem movimentos uniformes
numa mesma trajetória retilínea, e suas posições são representadas
a
seguir:
O encontro entre
os móveis ocorrerá no instante:
a) 4,0 s
b) 6,0 s
c) 8,0 s
d) 10 s
e) 12 s
06) Dois carros A e B de dimensões desprezíveis movem-se
em movimento uniforme e no mesmo sentido. No instante t =
0, os carros encontram-se nas posições indicadas na figura.
VA,B  VA  VB

VA,B  VA  VB
EM QUALQUER SITUAÇÃO:
VA, B
S
 A, B
t
Determine depois de quanto tempo A alcança B?
www.prevest.com.br – 3209-7300/3209-7240:
1
07) Dois carros percorrem uma pista circular, de raio R, no
mesmo sentido, com velocidades de módulos constantes e
iguais a V e 3V. O tempo decorrido entre dois encontros
sucessivos vale:
a) R/3v
b) 2R/3v
c) R/v
d) 2R/v
e) 3R/v
08) Dois navios, A e B, partem de um mesmo ponto e se
deslocam com velocidades de 35 km/h e 25 km/h, respectivamente. A comunicação entre os navios é possível, pelo
rádio, enquanto a distância entre eles não ultrapassar 600
km. Determine o tempo durante o qual os dois navios se
comunicam, admitindo que:
a) eles partem no mesmo tempo e se movem na mesma
direção e sentido;
b) eles partem no mesmo tempo e se movem na mesma
direção, mas em sentidos contrários;
c) eles partem no mesmo tempo e se movem em direções
perpendiculares entre si.
09) Um pequena esfera é lançada sobre uma superfície horizontal lisa e limitada por duas paredes paralelas. O lançamento é efetuado no instante t = 0 a partir de uma das paredes, de modo que a esfera realize sucessivas colisões frontais
com as paredes.
O gráfico espaço x
tempo do movimento oscilatório dessa
esfera,
desprezando-se a sua rotação
e as durações das colisões, é dado a seguir.
Pelo gráfico, nota-se que
nos choques, a perda de
energia cinética da esfera segue um certo padrão. Nesse ritmo, módulo da velocidade da
esfera logo após o 3º
choque será:
a) 10 cm/s
b) 12 cm/s
c) 27 cm/s
d) 40 cm/s
e) 80 cm/s
10) A posição de uma partícula, ao longo de sua trajetória, varia no
tempo conforme a tabela:
A função horária das posições desse movimento é:
a) s = 4 – 25t
b) s = 25 + 4t
c) s = 25 – 4t
d) s = – 4 + 25t
e) s = – 25 + 4t
11) (UF. AM) Um trem de 400m de comprimento, viaja com
velocidade escalar constante 72km/h e para atravessar um
túnel de 1,8km gasta um intervalo de tempo de:
a) 10 s
b) 1,0 min
c) 1min e 50 s
d) 200 s
12) (UEL) Um carro percorreu a metade de uma estrada
viajando a 30km/h e, a outra metade da estrada a 60km/h.
Sua velocidade escalar média no percurso total foi, em km/h,
de:
a) 54
b) 48
c) 45
d) 40
e) 38
13) (UDESC) Durante um teste de treinamento da Marinha,
um projétil é disparado de um canhão com velocidade constante de 275,0m/s em direção ao centro de um navio. O
navio move-se com velocidade constante de 12,0m/s em
direção perpendicular à trajetória do projétil. Se o impacto do
projétil no navio ocorre a 21,6m do seu centro, a distância
(em metros) entre o canhão e o navio é:
a) 322,2
b) 495,0
c) 516,6
d) 673,4
14) (Fuvest) A figura representa, em escala, a trajetória de
um caminhão de entregas que parte de A, vai até B e retorna
a A. No trajeto de A a B, o
caminhão mantém velocidade
escalar média de 30 km/h; na
volta, de B a A, gasta 6 min.
a) Qual o tempo gasto pelo
caminhão para ir de A até
B?
b) Qual a velocidade escalar
média do caminhão quando vai de B até A, em km/h?
15) (Unicamp) A figura abaixo mostra o esquema simplifica
do de um dispositivo colocado em uma rua para controle de
velocidade de automóveis (dispositivo popularmente chama
do de radar).
Os sensores S1 e S2 e a
câmera estão ligados a
um computa dor. Os
sensores enviam um
sinal ao computador
sempre que são pressionados pelas rodas de
um veículo. Se a velocidade do veículo está acima da permitida, o computador envia
um sinal para que a câmera fotografe sua placa
traseira no momento em
que esta estiver sobre a
linha tracejada. Para um
certo veículo, os sinais
dos sensores foram os
seguintes:
a) Determine a velocidade do veículo em km/h.
b) Calcule a distância entre os eixos do veículo.
01
B
11
C
02)
08)
14)
15)
RESPOSTAS
02
03
04
05
06
B
D
E
C
*
12
13
14
15
//
D
B
*
*
\\
t = 200 s
a) 60 h; b) 10 h; c) 13,9 h
a) t = 20 min; V = 60 km/h
a) V = 72 km/h; b) d = 3,0 m
07
C
//
\\
08
*
//
\\
09
A
//
\\
10
C
//
\\
DESAFIO
João e Maria apostam uma corrida numa pista circular de raio
R. A figura abaixo mostra a vista de cima dessa pista. João e
Maria deveriam partir do ponto A e seguir para B no sentido
horário. Porém, ele nota que ela esta em ótima forma e que
ele não teria a menor chance de ganhar a corrida. Em um ato
de desespero, ao largar, João resolve correr ao longo da
corda indicada na figura, chegando em B junto com Maria
(que correu ao longo da circunferência, conforme o combinado). O arco AB forma um ângulo de abertura .
Determine:
a) A razão entre as velocidades de João (VJ) e Maria (VM),
em função do ângulo . Para simplificar o problema, desconsidere a aceleração de largada e considere as velocidades escalares de ambos como constantes.
b)O valor da razão Vj/Vm se a medida do ângulo  for igual
a 60º
www.prevest.com.br – 3209-7300/3209-7240:
Resp: a) V =
; b) V =
2