MARCIO LUCATO
UMA PROPOSTA DE MODELAGEM PARA
SECADORES DE MACARRÃO DE CORTE
LONGO
SÃO CAETANO DO SUL
2009
MARCIO LUCATO
UMA PROPOSTA DE MODELAGEM
PARA SECADORES DE MACARRÃO DE CORTE
LONGO
Dissertação
apresentada
à
Escola
de
Engenharia Mauá do Centro Universitário do
Instituto Mauá de Tecnologia para obtenção do
título de Mestre em Engenharia de Processos
Químicos e Bioquímicos.
Linha de Pesquisa: Análise e Controle de
Processos Químicos
Orientador: Prof. Dr. Eduardo Lobo Lustosa
Cabral
SÃO CAETANO DO SUL
2009
Lucato, Marcio
Uma proposta de modelagem para secadores de macarrão de
corte longo / Marcio Lucato.—São Caetano do Sul, SP : CEUNEEM, 2009.
114 p.
Dissertação de Mestrado — Programa de Pós-Graduação. Linha
de Pesquisa: Análise e Controle de Processos Químicos — Escola
de Engenharia Mauá do Centro Universitário do Instituto Mauá de
Tecnologia.São Caetano do Sul, SP, 2009.
Orientador: Prof. Dr. Eduardo Lobo Lustosa Cabral
1. Macarrão de corte longo 2. Modelagem 3.
Secagem 4. Sistema de controle I. Instituto Mauá de
Tecnologia. Centro Universitário. Escola de Engenharia Mauá. II.
Título.
AGRADECIMENTOS
Ao Prof. Dr. Eduardo Lobo Lustosa Cabral, pela orientação, dedicação e amizade durante
a execução deste trabalho.
Ao Prof. Dr. Marcello Nitz, pela sugestão do tema, aulas sobre secagem e auxílio em
momentos importantes.
À Profª Edilene Amaral de Andrade Adell pelas correções no texto e auxílio com as tarefas
da coordenação.
Aos amigos, Prof. Sergio Kenji Moriguchi, pelo constante incentivo e pelas aulas que deu
em meu lugar e Prof. Dr. Ed Claudio Bordinassi, pelas aulas em que me substituiu e pelos
desenhos usados neste trabalho.
Ao Prof. Dr. Jose Maria Saiz Jabardo, pelo constante incentivo e discussões conceituais
sobre o tema.
Ao Prof. Dr. Leo Kunigk por todo o auxilio prestado, principalmente com a escolha do
periódico para a publicação do artigo.
Ao Prof. Dr. Marcos Costa Hunold, pelo auxílio com o Matlab.
Ao Prof. Dr. Gustavo Ferreira Leonhardt, pelas informações sobre fabrico e secagem de
macarrão.
Ao Prof. Dr. Mario Cavaleiro Fernandes Garrote, pelo incentivo.
À Helena, Carla, Paula e Marcela pelo companheirismo e compreensão pelo tempo que
tomei do nosso convívio para execução deste trabalho, e à Marcela também pela
digitação das equações.
Sobretudo a Deus pela oportunidade de realizar mais este trabalho.
RESUMO
Para a conservação do macarrão em temperatura ambiente, desde a fabricação até o
momento do consumo, sua umidade deve estar dentro de limites tais que impeçam sua
deterioração. O teor de umidade adequado é atingido em um processo de secagem em
equipamento industrial contínuo. A operação de um secador industrial consome grande
quantidade de energia. A otimização do consumo de energia pode ser feita pelo emprego
de um sistema de controle multivariável do tipo “Controle Ótimo”, baseado nos métodos do
espaço dos estados. Este estudo produz a modelagem do secador industrial na forma
adequada para servir de base para o projeto do sistema de controle multivariável e testa
seu desempenho por meio de simulação computacional.
ABSTRACT
To conserve dry pasta at room temperature, from manufacturing until consumption,
moisture content must be within certain limits to avoid deterioration. Adequate moisture
content is a consequence of the drying process in a continuous industrial dryer. Industrial
dryer operation demands large amount of energy. A multivariable control system based
on the “Optimal Control” state space method allows optimizing energy consumption. An
industrial dryer is modeled in this study in a convenient way to be used to design a
multivariable control system and tests model performance by means of computational
simulation.
SUMÁRIO
1.
2.
INTRODUÇÃO ........................................................................................................................................... 17
1.1.
DESCRIÇÃO DO PROBLEMA – PORQUE SECAR. ......................................................................................... 17
1.2.
PROCESSOS DE SECAGEM ........................................................................................................................ 17
1.3.
OBJETIVO ............................................................................................................................................... 19
REVISÃO BIBLIOGRÁFICA ................................................................................................................... 20
2.1.
SECADOR ................................................................................................................................................ 20
2.2.
SECAGEM ............................................................................................................................................... 25
2.3.
CINÉTICA DE SECAGEM DO MACARRÃO .................................................................................................. 31
2.4.
SECAGEM CONTÍNUA .............................................................................................................................. 36
2.5.
A QUESTÃO DO CONTROLE ..................................................................................................................... 38
2.5.1.
Teoria de controle moderno .......................................................................................................... 38
2.5.2.
Escolha .......................................................................................................................................... 40
2.6.
3.
METODOLOGIA ....................................................................................................................................... 42
3.1.
4.
DESCRIÇÃO ............................................................................................................................................. 43
DEFINIÇÃO DE UM TIPO DE SECADOR ............................................................................................ 48
4.1.
5.
MODELAGEM .......................................................................................................................................... 40
DESCRIÇÃO ............................................................................................................................................. 48
MODELAGEM ........................................................................................................................................... 50
5.1.
TEMPERATURA ....................................................................................................................................... 50
5.1.1.
Variação da energia interna da massa de ar úmido no VC........................................................... 51
5.1.2.
Energia transportada pelos fluxos de massa entrando e saindo do VC ........................................ 52
5.1.3.
Balanço de energia no VC............................................................................................................. 54
5.1.4.
Calor líquido trocado .................................................................................................................... 56
5.1.5.
Temperatura TE de entrada no trocador de calor ......................................................................... 61
5.1.6.
Umidade absoluta
5.2.
na entrada do trocador de calor .............................................................. 64
PRESSÃO................................................................................................................................................. 66
5.2.1.
Vazões de entrada e de saída de ar ............................................................................................... 68
5.3.
UMIDADE ABSOLUTA.............................................................................................................................. 72
5.4.
TEMPERATURA DE SAÍDA DA ÁGUA QUENTE........................................................................................... 74
5.4.1.
5.5.
6.
ωE
Cálculo da temperatura do ar úmido na saída do trocador de calor............................................ 78
UMIDADE DA PASTA ............................................................................................................................... 81
PROJETO BÁSICO DO SECADOR ........................................................................................................ 83
6.1.
PROCESSO DE SECAGEM ......................................................................................................................... 83
6.2.
CÁLCULO DOS PARÂMETROS DE OPERAÇÃO DO SECADOR ...................................................................... 84
6.2.1.
Umidade de equilíbrio ................................................................................................................... 84
6.2.2.
Umidade relativa ........................................................................................................................... 84
6.2.3.
Umidade absoluta.......................................................................................................................... 85
6.2.4.
Perda de umidade da pasta ........................................................................................................... 85
6.2.5.
Vazão de ar ambiente admitido ..................................................................................................... 86
6.3.
7.
SIMULAÇÃO E RESULTADOS............................................................................................................... 93
7.1.
8.
ESTUDO DO TROCADOR DE CALOR .......................................................................................................... 87
SIMULAÇÃO ............................................................................................................................................ 95
CONCLUSÕES ........................................................................................................................................... 98
8.1.
CONCLUSÕES SOBRE A ESCOLHA DO MODELO ......................................................................................... 99
8.2.
SUGESTÕES PARA TRABALHOS FUTUROS .............................................................................................. 100
LISTA DE FIGURAS
FIGURA 2.1-1– PRÉ-SECADOR (MILATOVICH E MONDELLI, 1990) ................................................................. 20
FIGURA 2.1-2 – DISTRIBUIÇÃO DE AR NO PRÉ-SECADOR (MILATOVICH E MONDELLI, 1990).......................... 21
FIGURA 2.1-3 – CIRCULAÇÃO DE AR NO PRÉ-SECADOR (MILATOVICH E MONDELLI, 1990)............................ 21
FIGURA 2.1-4 – DISTRIBUIÇÃO DE AR E FLUXO DE PASTA NO SECADOR (MILATOVICH E MONDELLI, 1990) ... 23
FIGURA 2.1-5 - LINHA DE SECAGEM PAVAN (MILATOVICH E MONDELLI, 1990) ............................................ 23
FIGURA 2.1-6 - LINHA DE SECAGEM BÜHLER PARA PASTA LONGA (MILATOVICH E MONDELLI, 1990)........... 23
FIGURA 2.1-7 – LINHA DE SECAGEM BRAIBANTI (MILATOVICH E MONDELLI, 1990) ..................................... 24
FIGURA 2.1-8 – SECADOR PAVAN (CATÁLOGO PAVAN S.P.A, 2007) ...................................................................... 24
FIGURA 2.2-1 – ISOTERMA CARACTERÍSTICA DE BIO-MATERIAL (KUDRA E STRUMILLO, 1998)....................... 25
FIGURA 2.2-2 – FORMAS DE ISOTERMAS PARA DIVERSOS MATERIAIS (KUDRA E STRUMILLO, 1998) ............... 29
FIGURA 2.2-3 – CURVA TÍPICA DE SECAGEM (KUDRA E STRUMILLO, 1998)..................................................... 30
FIGURA 3.1-1 – CURVA DE SECAGEM (CATÁLOGO PAVAN S.P.A.,2007)................................................................. 44
FIGURA 4.1-1 – CORTE TRANSVERSAL DO SECADOR PROPOSTO PARA MODELAGEM ............................................... 48
FIGURA 5.1-1 – VC CONTENDO A PASTA DENTRO DA CÉLULA ................................................................................ 56
FIGURA 5.1-2 – VC NA REGIÃO DA MISTURA DO AR ADMITIDO COM O RECIRCULADO ............................................ 61
FIGURA 8.1-1– MODELO DE SECADOR COM MISTURA APÓS O TROCADOR DE CALOR .............................................. 99
LISTA DE GRÁFICOS
GRÁFICO 2.3-1 - EFEITO DA TEMPERATURA NA DIFUSIVIDADE EFETIVA (VILLENEUVE E GÉLINAS 2006) ...... 34
GRÁFICO 2.3-2 - EFEITO DA UMIDADE RELATIVA NA DIFUSIVIDADE EFETIVA (VILLENEUVE E GÉLINAS 2006)
....................................................................................................................................................................... 34
GRÁFICO 2.3-3 - EFEITO DA TEMPERATURA NA UMIDADE DE EQUILIBRIO (VILLENEUVE E GÉLINAS 2006).... 35
GRÁFICO 2.3-4 -EFEITO DA UMIDADE RELATIVA NA UMIDADE DE EQUILÍBRIO (VILLENEUVE E GÉLINAS 2006)
....................................................................................................................................................................... 35
GRÁFICO 6.1-1 - CURVA DE SECAGEM CONFORME RECOMENDAÇÕES DE MILATOVICH E MONDELLI (1990) . 83
GRÁFICO 6.3-1 - VARIAÇÃO DO COEFICIENTE GLOBAL DE TROCA TÉRMICA ........................................................... 92
GRÁFICO 7.1-1 – VARIAÇÃO DAS TEMPERATURAS DO AR ÚMIDO ........................................................................... 95
GRÁFICO 7.1-2 – VARIAÇÃO DA UMIDADE RELATIVA ............................................................................................ 95
GRÁFICO 7.1-3 - VARIAÇÃO DA UMIDADE DE EQUILÍBRIO ...................................................................................... 96
GRÁFICO 7.1-4 – VARIAÇÃO DA UMIDADE MÉDIA DA PASTA AO SAIR DA CÉLULA .................................................. 96
GRÁFICO 7.1-5 – COMPARAÇÃO TE ALGÉBRICO X TE INTEGRADO .......................................................................... 97
LISTA DE TABELAS
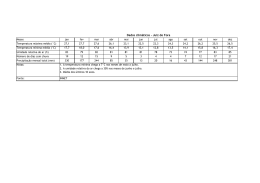
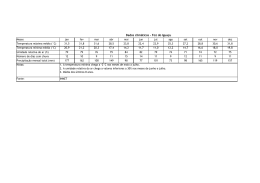
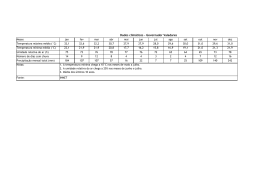
TABELA 3.1-1 – PROCESSO DE SECAGEM DO SECADOR PAVAN .............................................................................. 45
TABELA 3.1-2 – COMPARAÇÃO DE MODELOS DE ISOTERMA. .................................................................................. 46
TABELA 5.2-1 – COEFICIENTE DE PERDA DE CARGA PARA DAMPER TIPO BORBOLETA ............................................ 71
TABELA 5.2-2 – COEFICIENTE DE PERDA DE CARGA PARA DUTO INSTALADO EM PAREDE. ..................................... 72
TABELA 6.1-1 - PARÂMETROS DE OPERAÇÃO DO SECADOR .................................................................................... 84
TABELA 6.3-1 – VALOR DO CALOR ESPECIFICO DO AR ÚMIDO PARA DIVERSAS CONDIÇÕES ................................... 88
TABELA 6.3-2 – TEMPERATURAS DE ENTRADA E DE SAÍDA DO TROCADOR DE CALOR ............................................ 89
TABELA 6.3-3 – VAZÃO DE ÁGUA QUENTE ............................................................................................................. 90
TABELA 6.3-4 – VALORES DE CAPACIDADE DE TROCA TÉRMICA ( UA ) ................................................................. 90
TABELA 6.3-5 – ÁREA NECESSÁRIA PARA CADA SITUAÇÃO AMBIENTE EXTREMA .................................................. 91
TABELA 6.3-6 – VARIAÇÃO DO COEFICIENTE GLOBAL DE TROCA TÉRMICA ............................................................ 91
LISTA DE ANEXOS
ANEXO 1 – CÁLCULO DA CAPACIDADE TÉRMICA ............................................................................................... 102
ANEXO 2 – CÁLCULO DO COEFICIENTE GLOBAL DE TROCA TÉRMICA ................................................................. 103
ANEXO 3 – DIAGRAMAS DE BLOCO NO SIMULINK .............................................................................................. 108
ANEXO 4 – PAINEL DE CONTROLE NO SIMULINK ................................................................................................ 112
LISTA DE SÍMBOLOS
S - área da seção transversal do duto
A - área de troca do trocador de calor
a A - atividade do vapor de água
cpar TE - calor específico a pressão const. do ar úmido na entrada do trocador de calor
cpg - calor específico a pressão constante do ar seco
cp A - calor específico a pressão constante do vapor de água
cp0 ar - calor específico a pressão constante, do ar úmido, à temperatura T0, referido à
massa de ar seco
cvg - calor específico a volume constante do ar seco
cv A - calor específico a volume constante do vapor de água
cvar - calor específico a volume constante, do ar úmido, à temperatura T, referido à
massa de ar seco
c aq - calor específico da água quente
cm - calor específico do metal do trocador de calor
Cc - capacidade calorífica da corrente fria
Ch - capacidade calorífica da corrente quente
C - coeficiente de perda de carga da transição do secador para o duto de saída
C (θ ) - coeficiente de perda de carga variável em função do ângulo de abertura do
“damper”
U - coeficiente global de troca do trocador de calor
R0 ar - constante de gás ideal do ar ambiente, referida à massa de ar seco
Rar TE - constante de gás ideal do ar úmido na entrada do trocador de calor
Rar - constante de gás ideal do ar, dentro da célula, referida à massa de ar seco
Rg - constante de gás perfeito para ar seco
RA - constante de gás perfeito para vapor de água
ρ 0 ar
ρ ar
- densidade do ar ambiente externo ao secador
- densidade do ar úmido interno ao secador
∆f (Vi ) - diferença entre o valor da função f (Vi ) e o valor da função f (Vi 0 )
D - difusividade efetiva da umidade
ωE ω
}
cpar - é o calor especifico médio entre as condições ωE , TE e ω , T , do ar úmido
ω E ω0
}
cpar - é o calor especifico médio entre as condições ωE , TE e ω0 , T0 , do ar úmido
ε
- efetividade
uaq - energia interna média da água quente dentro do trocador de calor
uar - energia interna media do ar
u g - energia interna média do ar seco contido na célula
um - energia interna média do metal do trocador de calor
uA
- energia interna média do vapor de água contido na célula
hAl - entalpia da água (líquido saturado)
hAv - entalpia da água (vapor saturado)
haqe - entalpia da água quente entrando no trocador de calor
haq s - entalpia da água quente saindo do trocador de calor
hA lv - entalpia de evaporação da água, à temperatura do ar úmido da célula
h ge - entalpia do ar seco entrando na célula
h gs - entalpia do ar seco saindo da célula
hge TC - entalpia do ar seco, entrando no trocador de calor
hgs TC - entalpia do ar seco, saindo do trocador de calor
hP 0 - entalpia do macarrão ao entrar na célula
hP 0 - entalpia do macarrão ao entrar na célula
hP - entalpia do macarrão ao sair da célula
hP - entalpia do macarrão ao sair da célula
hAe TC - entalpia do vapor de água contido no ar úmido entrando no trocador de calor
hAs TC - entalpia do vapor de água contido no ar úmido saindo do trocador de calor
h Ae - entalpia do vapor de água, contido no ar úmido, entrando na célula
h As - entalpia do vapor de água, contido no ar úmido, saindo da célula
hg - entalpia média do ar seco no interior da célula
har e - entalpia média do ar úmido do ambiente externo, admitido na célula
har TE - entalpia média do ar úmido entrando no trocador de calor
har - entalpia média do ar úmido no interior da célula
hA - entalpia média do vapor de água no interior da célula
ξ
- fator de correção
Q& liq - fluxo de calor através da fronteira do volume de controle
Q& PASTA - fluxo de calor trocado com a pasta
Q&TC - fluxo de calor trocado com o trocador de calor
m& P - fluxo de macarrão, base seca, que passa pelo secador
m& Pu - fluxo de macarrão, base úmida, que passa pelo secador
y A - fração molar do vapor de água no ar
f A0 - fugacidade da água livre à pressão da mistura
f A - fugacidade do vapor de água
f A - fugacidade parcial do vapor de água
M aq - massa de água quente dentro do trocador de calor
m& AP - massa de água trocada com o macarrão
M g - massa de ar seco contido na célula
M gE - massa de ar seco no volume de controle antes do trocador de calor
M ar - massa de ar úmido no volume de controle
mS - massa de material seco
M m - massa de metal do trocador de calor
mA - massa de vapor de água
M A - massa de vapor de água contido no ar dentro da célula
M A E - massa de vapor de água no volume de controle antes do trocador de calor
L - percurso da pasta dentro de cada célula
∆P - perda de carga causada pela singularidade em questão
Patm - pressão atmosférica do ambiente externo ao secador
pv - pressão de saturação do vapor d’água
P - pressão do ar úmido no interior da célula
Pvent - pressão na sucção do ventilador de exaustão
pg - pressão parcial do ar seco
p A - pressão parcial do vapor de água
β1
- primeira raiz característica da função de Bessel da primeira espécie e ordem zero
R p - raio do espaguete
Sr (Vi ) - sensibilidade relativa da variável Vi
T0 - temperatura (de bulbo seco) do ar ambiente (externo ao secador)
T - temperatura (de bulbo seco) do ar dentro da célula
Tbs - temperatura de bulbo seco do ar de secagem
Tbu - temperatura de bulbo úmido do ar de secagem
Taqe - temperatura de entrada da água quente
TE - temperatura de entrada do ar úmido no trocador de calor
Tc ,i - temperatura de entrada do fluido frio
Th ,i - temperatura de entrada do fluido quente
Taq s - temperatura de saída da água quente
Tc ,o - temperatura de saída do fluido frio
Th,o - temperatura de saída do fluido quente
TT - temperatura do ar úmido de saída do trocador de calor
T0 - temperatura do meio ambiente
Taq - temperatura média da água quente
Tm - temperatura média do metal do trocador de calor
t - tempo
ω0
ω
- umidade absoluta do ar ambiente (externo ao secador)
- umidade absoluta do ar dentro da célula
ω0
- umidade absoluta do meio ambiente
ωE
- umidade absoluta média na entrada do trocador de calor
X e - umidade de equilíbrio (do macarrão)
X - umidade final da pasta ao sair da célula
X 0 - umidade inicial da pasta ao entrar na célula
ϕ
- umidade relativa
m& AP - umidade trocada entre a pasta e o ar do interior da célula
Vi 0 - valor de referência da variável Vi
ui - variável de controle (entrada)
xi - variável de estado
m& aq - vazão de água quente
m& g - vazão de ar de seco
m& g TC - vazão de ar seco através do trocador de calor
m& P - vazão de pasta base seca
m& A TC - vazão de vapor de água contido no ar úmido através do trocador de calor
m& gTC - vazão do ar seco através do trocador de calor
m& aqe - vazão em massa da água quente entrando no trocador de calor
m& aq s - vazão em massa da água quente saindo do trocador de calor
m& g - vazão em massa de ar seco
m& ge TC - vazão em massa de ar seco, entrando no trocador de calor
m& gs TC - vazão em massa de ar seco, saindo do trocador de calor
mar e - vazão em massa de ar úmido admitido na célula
marTC - vazão em massa de ar úmido através do trocador de calor
mar s - vazão em massa de ar úmido saindo da célula
m& Ae TC - vazão em massa de vapor de água contido no ar entrando no trocador de calor
m& As TC - vazão em massa de vapor de água contido no ar saindo do trocador de calor
m& gTC - vazão em massa do ar seco contido no fluxo de ar úmido através do trocador de
calor
m& gv - vazão em massa do ar seco contido no fluxo de ar úmido provocado pelos
ventiladores de circulação do ar da célula
m& ar - vazão em massa do ar úmido
m& ge - vazão em massa do ar, base seca, que entra na célula
m& gs - vazão em massa do ar, base seca, que sai da célula
m& A - vazão em massa do vapor de água contido no ar úmido
m& Ae - vazão em massa do vapor de água contido no ar úmido admitido na célula
m& As - vazão em massa do vapor de água contido no ar úmido saindo da célula
m& Av - vazão em massa do vapor de água contido no fluxo de ar úmido provocado pelos
ventiladores de circulação do ar da célula
m& A TC - vazão em massa do vapor de água contido no fluxo de ar úmido através do
trocador de calor
m& AP - vazão em massa do vapor de água, trocado pela pasta, que entra no volume de
controle
mar v - vazão em massa dos ventiladores de circulação (total)
v&ar - vazão em volume do ar
V - velocidade do ar passando pela singularidade
V - volume da célula
1. INTRODUÇÃO
1.1.
DESCRIÇÃO DO PROBLEMA
– PORQUE SECAR.
O macarrão é uma massa alimentícia que ao ser produzida apresenta uma elevada
umidade, expressa em massa de água por massa de macarrão seco, da ordem de 43%
ou até superior. Não pode, assim, ser armazenada à temperatura ambiente sem se
degradar. Para que possa ser armazenada e comercializada de forma conveniente a
massa deve ser seca a teores de umidade da ordem de 15% ou inferiores.
Atualmente, a indústria alimentícia emprega linhas contínuas para a produção dos
diversos tipos de macarrão, sendo o secador o equipamento que realiza uma das fases
finais do fabrico. Após a secagem, vem um resfriador para trazer a massa1 à temperatura
ambiente para que possa ser armazenada até o momento de ser embalada. Após o
resfriador, há um setor de ensilagem que serve de pulmão para igualar as vazões da
linha de fabricação e a de embalagem.
1.2.
PROCESSOS DE SECAGEM
A qualidade da massa alimentícia produzida está diretamente ligada ao processo
de secagem, portanto, a uma sequência de tempo de exposição a uma determinada
temperatura e umidade relativa. A qualidade é consequência de uma escolha e controle
adequados do processo. O processo de secagem evoluiu ao longo do tempo, passando do
emprego de temperaturas, na faixa de 40 a 55ºC, para valores mais elevados, na faixa
de 85 a 90ºC.
Segundo ORMENESE et al. (1998), em comparação com o processo tradicional em
baixa temperatura, a secagem em temperatura mais alta apresenta as seguintes
vantagens e desvantagens:
1
Neste texto os termos massa e pasta são empregados como sinônimos de
macarrão.
17
1. a produtividade é maior devido ao tempo de secagem menor, o que
também resulta em equipamentos mais compactos e de menor custo;
2. os macarrões secos através dos processos de alta temperatura apresentam
melhor cor e melhores características de cozimento (maior firmeza, menor
perda de sólidos e menor gomosidade);
3. quando se tratar de massas com ovos, há o risco de contaminação por
microrganismos patogênicos (Salmonela e S. aureus) que somente são
eliminados com temperaturas acima de 60ºC, atingidas na secagem em
alta temperatura; e
4. há uma perda nutricional associada à perda maior de lisina disponível na
secagem em alta temperatura.
MILATOVICH e MONDELLI (1990) classificam os processos de secagem em três
tipos:
−
processo tradicional a baixa temperatura, em torno de 50ºC, necessitando de
cerca de 48 horas para a secagem completa;
−
processo a alta temperatura, na faixa de 65-75ºC, completando a secagem em
12-17 horas;
−
processo a altíssima temperatura, superior a 86ºC, chegando a 90-105ºC. Nesse
caso o tempo de secagem para pasta longa, é cerca de 5 horas.
A tendência atual é o emprego do processo de secagem a altíssima temperatura,
devido à maior produtividade, melhor qualidade do produto e menor risco de
contaminação.
A qualidade da pasta, produzida em equipamentos como os descritos, depende do
ajuste adequado da temperatura e da umidade relativa de secagem, em cada célula do
secador, de forma que a massa, que atravessa o equipamento em um fluxo contínuo e
constante, passe pelas diversas fases que o processo de secagem exige.
18
O processo de secagem é composto de diferentes fases, cada uma delas
caracterizada pela temperatura e umidade relativa do ar que envolve o fluxo de massa e
pelo tempo de exposição da massa a essa condição de umidade e temperatura. O tempo
de exposição é definido pelo comprimento de cada célula e pela velocidade de transporte
da pasta, que são características construtivas da máquina.
Já a temperatura e a umidade relativa do ar interno à célula podem ser ajustadas.
O ar externo que é admitido na célula, vem do ambiente da fábrica, portanto
condicionado a uma temperatura bem inferior àquela exigida pelo processo de secagem,
é aquecido em um trocador de calor, que usa água quente como fluido quente. De forma
que sua temperatura pode ser controlada por meio da variação da vazão de água quente.
A umidade relativa, que tende a aumentar à medida que o ar interno à célula
incorpora a umidade cedida pela massa, pode ser controlada pela admissão de ar mais
seco advindo do ambiente externo ao secador. Há exaustores com suas sucções ligadas
às células de maneira a garantir uma pressão interna abaixo da pressão atmosférica,
assim a vazão de ar mais seco, admitido para abaixar o teor de vapor de água no ar
interno, pode ser controlada através de um “damper”.
O controle da temperatura e da umidade relativa do ar dentro de cada célula, é de
extrema importância para a obtenção da qualidade desejada para a pasta produzida.
Existem diversos tipos de sistemas de controle. Os mais indicados para controle
de equipamentos que trabalhem com processos cujas variáveis sejam acopladas são os
sistemas de controle projetados com o uso dos métodos do espaço dos estados.
O projeto de um sistema de controle necessita partir de um modelo que descreva
o processo a ser controlado.
1.3.
OBJETIVO
O objetivo deste trabalho é modelar o processo de secagem de macarrão em
secador contínuo, de maneira a obter um modelo na forma adequada para ser linearizado
e usado para o projeto do sistema de controle.
19
2. REVISÃO BIBLIOGRÁFICA
2.1.
SECADOR
Nas linhas modernas, a secagem é feita em equipamentos com características
próprias. O transporte da massa ao longo do secador, no caso da massa longa, é feito
por meio de varas de metal conduzidas por correntes, sobre as quais os fios de macarrão
são estendidos, caindo metade do comprimento para cada lado.
O processo de secagem a alta temperatura é constituído de duas fases, présecagem e secagem, conforme MILATOVICH e MONDELLI (1990), descritas conforme
segue.
A pré-secagem é uma fase muito delicada e crítica, da qual depende o êxito final
do processo. O pré-secador é praticamente um túnel construído em um só nível,
conforme ilustrado na Figura 2.1-1, no qual a pasta entra com uma elevada umidade em
um ambiente úmido e quente. Nesta fase a pasta perde um percentual significativo de
umidade. O ar de secagem é aquecido em trocadores de calor, nos quais o fluido quente
é água aquecida.
Figura 2.1-1– Pré-secador (MILATOVICH E MONDELLI, 1990)
O ar é forçado através da camada de massa a secar por meio de ventiladores
centrífugos, distribuídos ao longo da largura do secador em quantidade suficiente para
garantir uma uniformidade no fluxo de ar, conforme mostrado na figura 2.1-2.
.
20
Figura 2.1-2 – Distribuição de ar no pré-secador (MILATOVICH e
MONDELLI, 1990)
Chapas de metal curvadas formam defletores que guiam o ar de forma que, após
passar pela massa a secar, é desviado no sentido longitudinal do secador até encontrar
outro defletor que o obriga a subir atravessando novamente a camada de pasta,
conforme se pode ver na figura 2.1-3.
Figura 2.1-3 – Circulação de ar no pré-secador (MILATOVICH e MONDELLI,
1990)
A manutenção da umidade interna do ar no pré-secador e a eliminação do excesso
com a conseqüente reposição de ar externo é feita por meio de outros ventiladores
centrífugos instalados externamente ao túnel do pré-secador. O seu funcionamento é
automático e controlado por um sensor de umidade colocado próximo à zona de
aspiração.
21
A fase de secagem pode ser feita por diferentes tipos de secadores, MILATOVICH
e MONDELLI (1990) descrevem um dos tipos:
O esquema da figura 2.1-4 refere-se ao critério de distribuição de ar e de
posicionamento dos grupos de ventilação na galeria de secagem de uma linha THT
(secagem a altíssima temperatura) para pasta longa produzida pela empresa Pavan
S.p.A. tradicional fabricante de secadores para pastifícios. O secador é composto de três
planos sobrepostos e termicamente independentes. A largura, comprimento e número
dos planos variam segundo a produção horária da linha. Para baixas produções,
usualmente, a galeria de secagem é composta de um só plano.
No exemplo indicado, a massa percorre os planos do secador de baixo para cima,
passando sob as centrais de ventilação, cada uma das quais composta de:
−
um ou mais ventiladores centrífugos, conforme a largura da linha, instalados
acima da massa de forma a fornecer um fluxo de ar uniforme;
−
um trocador de calor usando água quente como fluido quente para aquecer o ar,
colocado acima da massa. A circulação de água é controlada por uma válvula
acionada por um painel de controle;
−
uma unidade de condensação, constituída de um trocador de calor a água fria,
colocado abaixo da linha da massa. Também aqui a circulação de água é
controlada por uma válvula acionada por um painel de controle;
−
um sistema de emissão de vapor constituído por circuito ligado a um pulverizador
montado próximo ao trocador de calor de aquecimento. A admissão de vapor é
modulada por uma válvula comandada pelo sistema de controle automático em
função da umidade relativa medida por um sensor.
O texto citado não esclarece a finalidade da injeção de vapor. Como o texto é de 1990 e
o catálogo atual do mesmo equipamento afirma que as condições de secagem prédefinidas são alcançadas sem a injeção de vapor, pode-se supor que o sistema de
controle do equipamento descrito em 1990 não era muito eficiente, pois precisava
corrigir uma retirada excessiva de umidade, na unidade de condensação, com uma
injeção de vapor no ar de secagem antes do mesmo voltar a ter contato com a pasta.
22
Figura 2.1-4 – Distribuição de ar e fluxo de pasta no secador (MILATOVICH e
MONDELLI, 1990)
A concepção da linha de secagem conforme diferentes fabricantes parece não
apresentar variações de conceito de funcionamento, mas apenas detalhes de projeto,
como mostram as figuras 2.1-5, 6 e 7.
Figura 2.1-5 - Linha de secagem Pavan (MILATOVICH e MONDELLI, 1990)
Figura 2.1-6 - Linha de secagem Bühler para pasta longa (MILATOVICH e
MONDELLI, 1990)
23
Figura 2.1-7 – Linha de secagem Braibanti (MILATOVICH e MONDELLI, 1990)
A figura 2.1-7 mostra a linha de secagem Braibanti, também para pasta longa. Da
mesma forma podem-se notar ventiladores provocando fluxo de ar transversal ao
percurso da massa, passando por trocadores de calor.
A análise de catálogos atuais de secadores mostra que esses secadores descritos
por MILATOVICH e MONDELLI (1990) há quase duas décadas não apresentaram
mudanças significativas de projeto, como pode ser notado na figura 2.1-8, extraída do
catálogo atual da Pavan. O catálogo informa também que a secagem desejada é obtida
sem a emissão de vapor. Anteriormente usada, como descrito por MILATOVICH e
MONDELLI (1990), foi abandonada, provavelmente, para evitar contaminação da massa,
ou talvez o sistema atual de controle prescinda da adição de vapor para controle da
umidade.
Figura 2.1-8 – Secador Pavan (catálogo Pavan S.p.A, 2007)
24
2.2.
SECAGEM
Do ponto de vista de engenharia de processo, secagem é uma transferência,
através de uma interface, de massa (umidade) do material úmido para o gás que o
envolve (ar) que pode ser idealizada pelo transporte de umidade líquida do núcleo do
material para sua superfície, seguido pela evaporação do líquido da superfície do
material, e a dissipação do vapor de água em uma quantidade de gás. Quando o mesmo
volume de ar permanece em contato com o material úmido sob pressão e temperatura
constantes (condições estáticas), a umidade é transferida através da interface até que as
respectivas concentrações em massa nas fases líquida e gasosa estejam em equilíbrio
termodinâmico (KUDRA e STRUMILLO, 1998).
Macarrão é um bio-material. Ainda segundo KUDRA e STRUMILLO (1998),
qualquer bio-material pode ser visto como uma estrutura sólida preenchida com uma
certa quantidade de água independente da origem do material e de sua umidade
inicial/final. Do ponto de vista da secagem há dois tipos de umidade: não ligada e ligada.
Umidade não ligada é aquela cuja pressão de vapor é a mesma que para a
superfície livre do líquido puro. Umidade interna em material não higroscópico é não
ligada, assim como a umidade que excede a umidade de equilíbrio em materiais
higroscópicos. A figura 2.2-1 apresenta o conteúdo de umidade X em função da umidade
relativa do ar ϕ , e os tipos de ligação de umidade.
CONTEÚDO DE UMIDADE X
UMIDADE NÃO
LIGADA
UMIDADE LIVRE
UMIDADE LIGADA
(HIGROSCÓPICA)
UMIDADE DE
EQUILÍBRIO
UMIDADE RELATIVA DO AR
Figura 2.2-1 – Isoterma característica de bio-material (KUDRA e STRUMILLO,
1998)
Umidade ligada (higroscópica ou dissolvida) é definida pelo líquido que exerce
uma pressão de vapor menor que a do líquido puro na dada temperatura.
25
A secagem, que é a retirada da umidade do bio-material, depende das condições
do ar do ambiente no qual o material está imerso. Então o estudo do processo de
secagem envolve o estudo das propriedades do ar úmido.
Como os processos de secagem se dão, usualmente, à pressão atmosférica, ou
próxima dela, o ar úmido pode ser visto como um gás ideal. As seguintes propriedades
são importantes neste estudo:
−
Umidade absoluta ( ω), é a concentração de vapor de água no ar úmido
expressa como a massa de água por unidade de massa de ar seco.
ω=
mA
mg
2.2-1
na equação 2.1-1 mA é a massa de vapor de água e mg é a massa de ar
seco;
−
Umidade relativa (ϕ), é a concentração de vapor de água definida como a
razão da massa do vapor de água pela massa máxima de vapor possível na
mesma temperatura (condição de saturação). Para um gás ideal pode ser
definida como a razão da pressão parcial do vapor de água pA pela pressão
máxima de vapor pv (pressão de saturação) na mesma temperatura.
ϕ=
pA
pv
2.2-2
A umidade relativa é função da pressão de saturação do vapor de água, que por
sua vez, é função da temperatura (mantida a pressão total, usualmente a pressão
atmosférica), portanto, para uma mesma condição de umidade absoluta, pode-se
controlar a umidade relativa pela temperatura da mistura gasosa.
A umidade absoluta, mantida a hipótese de gás ideal para a mistura gasosa, pode
ser expressa em termos das pressões parcial e total do ar na mistura. A massa de vapor
de água à pressão pA e temperatura T pode ser calculada por:
mA =
p AV
RAT
2.2-3
na qual, V é o volume da mistura e RA é a constante de gás ideal para vapor de água e a
massa de ar seco pode ser calculada por:
26
mg =
p gV
2.2-4
Rg T
na qual, pg é a pressão parcial do ar seco, Rg é a constante de gás ideal para ar seco.
Substituindo mA e mg na equação 2.2-1 e levando em consideração que RA = 461,5
J/kg—K Rg = 287 J/kg—K tem-se:
ω=
Rg p A
RA pg
= 0, 622
pA
( P − pA )
2.2-5
A umidade absoluta pode ser também expressa em termos da umidade relativa
substituindo em 2.2-5 o valor de pA calculado em 2.2-2:
ω = 0, 622
Usualmente
os
materiais
ϕ pv
P − ϕ pv
em
processo
2.2-6
de
secagem
são
descritos
como
constituídos por uma estrutura completamente seca e uma certa quantidade de umidade,
principalmente no estado líquido. Essa quantidade de umidade é usualmente expressa
como umidade em base seca, que é a massa de umidade mA por unidade de massa do
material seco mS:
X=
mA
mS
2.2-7
Associada à função de Gibbs é definida a fugacidade, que é uma propriedade
termodinâmica importante no estudo de gases reais. Citando VAN WYLEN e SONNTAG
(1993): ”A fugacidade é essencialmente uma pseudo-pressão. Quando é substituída pela
pressão pode-se, com efeito, usar para os gases reais as mesmas equações que são
normalmente usadas para os gases ideais”.
Atividade de água
a A é uma propriedade relacionada com o conteúdo de umidade
ligada do bio-material.
27
aA =
na qual
fA
f A0
(VAN WYLEN e SONNTAG, 1993)
2.2-8
f A é a fugacidade (parcial) do vapor de água no bio-material e f A0 é a
fugacidade da água livre (substância pura) à pressão da mistura.
Se a mistura (ar úmido) puder ser admitida como solução ideal (a variação de
volume na mistura é desprezível) à pressão P, assim como a P0 segue-se:
aA =
yA f A
f A0
2.2-9
Para mistura de gases ideais (ar úmido à pressão atmosférica) a equação 2.2-9
pode ser escrita:
aA =
yA P pA
= 0
P0
P
2.2-10
na qual yA é a fração molar de vapor de água P é a pressão total do gás (ar) e P0
pressão da água livre (para as fases líquido e vapor nos sistemas difásicos, o estado de
referência para cada componente é tomado como da substância pura naquela fase e à
pressão da mistura).
Como a pressão da água próxima a sua superfície livre é a pressão de saturação
pv , vem:
aA =
pA pA
=
=ϕ
P 0 pv
2.2-11
Segundo KUDRA e STRUMILLO (1998), embora a definição de atividade de água
seja similar àquela de umidade relativa do ar ϕ, estes dois parâmetros são iguais apenas
no equilíbrio termodinâmico. Na prática de secagem, no entanto, a atividade de água é
frequentemente sinônimo de umidade relativa do ar porque sob condições típicas de
secagem as diferenças entre ambas quantidades é menor que 0,2% (GAL,1972 citado
por KUDRA e STRUMILLO ,1998).
28
Mantida a temperatura constante, o conteúdo de umidade no material, dado pela
umidade em base seca X, é função da atividade de água do material. Essa função
CONTEÚDO DE UMIDADE X
depende das características do material úmido, como ilustrado na figura 2.2-2.
ATIVIDADE DE AGUA
Figura 2.2-2 – Formas de isotermas para diversos materiais
(KUDRA e STRUMILLO, 1998)
No processo de secagem podem-se distinguir alguns valores característicos de
conteúdo de umidade do material:
−
umidade inicial X0 - é a umidade do material no início do processo de secagem;
−
umidade de equilíbrio Xe - é a umidade em equilíbrio com o vapor de água contido
no ar de secagem. Esta é a umidade mínima teórica que pode ser obtida no
processo de secagem;
−
umidade higroscópica máxima Xmax - é a máxima umidade de equilíbrio quando o
ar de secagem está saturado.
Quanto ao processo de secagem, as seguintes fases podem ser percebidas, em
função dos valores da umidade em base seca (X) do material e da umidade relativa (ϕ)
do ar de secagem:
29
−
secagem controlada pelas condições externas – a resistência à transferência de
massa na interface ar-material predomina e a velocidade de secagem depende
dos coeficientes de transferência de calor e de massa na superfície do material e
das condições do ar (temperatura e umidade relativa).
−
secagem controlada pelas condições internas – a resistência à transferência de
massa através do material predomina e a velocidade de secagem é fortemente
influenciada pelas propriedades do material úmido, como a difusividade da água
no material, sua temperatura e a diferença entre sua umidade e a umidade de
equilíbrio.
No processo de secagem, mais importante do que o estudo da dinâmica de
secagem (que caracteriza os perfis de temperatura e umidade através do material) é o
conhecimento da cinética de secagem do material, que descreve as variações da umidade
e da temperatura médias com o tempo.
A cinética de secagem é tipicamente mostrada em um diagrama da umidade
CONTEÚDO D EUMIDADE X
média em função do tempo, como ilustrado na figura 2.2-3.
TEMPO
Figura 2.2-3 – Curva típica de secagem (KUDRA e STRUMILLO, 1998)
30
O trecho AC da curva representa a fase de secagem controlada pelas condições
externas. O percurso inicial AB, com velocidade de secagem crescente, representa o
espaço de tempo necessário para elevação da temperatura do material de uma
temperatura inicial T0 à temperatura de bulbo úmido do ar de secagem Tbu. No trecho BC
o material já atingiu a temperatura de bulbo úmido do ar de secagem e nela permanece,
devido ao processo de evaporação adiabático, até o fim da fase que se dá quando toda a
umidade não ligada tiver sido retirada. Nesse trecho a velocidade de secagem é
constante. No trecho CD o processo de secagem é controlado pelas condições internas. A
temperatura do material, inicialmente igual à de bulbo úmido do ar de secagem, vai
gradualmente, à medida que o material perde umidade, subindo até próximo da
temperatura de bulbo seco, tão mais próximo quanto maior for o tempo de exposição
àquelas condições. A velocidade de secagem vai decrescendo à medida que a umidade do
material aproxima-se da umidade de equilíbrio.
2.3.
CINÉTICA DE SECAGEM DO MACARRÃO
Segundo ANDRIEU et al. (1985), citando Andrieu e Stamatopoulos (1984), o
processo de secagem do macarrão, conforme dados colhidos em experimentos, é
controlado pelas condições internas do material e a velocidade de secagem depende da
umidade de equilíbrio na sua superfície.
ANDRIEU et al. (1985) estabeleceram um modelo para a isoterma de espaguete,
obtido por extrusão, ajustando a relação empírica de Oswin a dados experimentais.
Foram tentadas outras expressões, mas a que melhor se adaptou a todo o intervalo
desejado 0,10 <
aA <0,90, com um erro relativo médio entre o valor calculado pela
relação entre o valor calculado e o valor medido no experimento de 6,3%. A relação
obtida foi a seguinte:
 a 
X e = (0,154 − 1, 22 × 10 −3 × T )  A 
 1 − aA 
( 0,078+ 7,32×10
−3
×T
)
2.3-1
31
na qual Xe é a umidade de equilíbrio, ou seja, o menor teor de umidade que a pasta pode
atingir naquela condição de umidade relativa e temperatura do ar no qual ela está
imersa, T é a temperatura, expressa em graus Celsius, e
aA é atividade de água na
pasta.
Embora tenha sido o primeiro estudo visando estabelecer a variação da umidade
de equilíbrio com a atividade de água para diversas temperaturas, ainda não se tem
expressão mais precisa para esse fim. VILLENEUVE e GÉLINAS (2006), citando PONSART
et al. (2003), constataram que a relação empírica de OSWIN é a que melhor se adequou
para
descrever
a
isoterma
para
pasta,
e
determinaram
experimentalmente
as
constantes, resultando a expressão:
 a 
X e = (0,1522 − 1, 247 × 10−3 × T )  A 
 1 − aA 
(0,08883+7,892×10
−3
×T
)
2.3-2
que, pode-se notar, não apresenta uma diferença significativa para a primeira.
Note-se que, embora as equações 2.3-1 e 2.3-2 forneçam Xe em função da
aA, na prática de secagem, no entanto, a atividade de água é frequentemente
atividade
substituída pela umidade relativa do ar porque sob condições típicas de secagem as
diferenças entre ambas quantidades é menor que 0,2% (GAL,1972 citado por KUDRA e
STRUMILLO ,1998).
Outro ponto do estudo original de ANDRIEU e STAMATOPOULOS (1986)
confirmado por VILLENEUVE e GÉLINAS (2006) é a expressão para determinar a variação
da umidade média do espaguete em função do tempo, obtida a partir da Lei de Fick,
dada por:
 β 2 Dt 
X − Xe
4
= 2 exp  − 1 2 
 Rp 
X 0 − X e β1


na qual
2.3-3
X é a umidade média, X0 é a umidade inicial, β1 é o primeiro auto valor da
equação de Bessel, D é a difusividade efetiva da água no espaguete e Rp é o raio do
espaguete.
32
A umidade de equilíbrio
X e e a difusividade efetiva D são parâmetros
importantes no estudo da umidade média da pasta no processo de secagem, ambas
variam em função da temperatura e da umidade relativa do ar no qual a pasta está
imersa.
Um importante avanço na área, introduzido por VILLENEUVE e GÉLINAS (2006),
foi o estudo de sensibilidade da difusividade efetiva da água na pasta e da umidade de
equilíbrio com a variação da temperatura e da umidade relativa.
VILLENEUVE e GÉLINAS (2006) usaram o método de diferenças finitas, proposto
por CHOKMANI, VIAU e BOURGEOIS (2001) para o cálculo da sensibilidade relativa.
A analise de sensibilidade determina os efeitos da variação do parâmetro de
entrada na variação da saída do modelo. Usando um cenário de referência, os
parâmetros de entrada são variados um a um dentro de um intervalo específico.
Parâmetros de entrada críticos são expressos como % de variação na saída do modelo
por unidade de mudança do parâmetro de entrada. Sensibilidade relativa não é
influenciada por unidades ou escalas dos parâmetros de entrada.
 ∆f (Vi ) 
Vi 0
Sr (Vi ) = 

0
 ∆Vi V j0, j≠i f (Vi )
2.3-4
Sr (Vi ) é a sensibilidade relativa da variável Vi , ∆f (Vi ) é a diferença entre o valor da
f (Vi ) e o valor da função f (Vi 0 ) , Vi 0 é o valor de referência da variável Vi .
função
O estado de referência foi secagem a 40ºC e
ϕ
= 65%. A temperatura foi
incrementada de 1ºC no intervalo de 41 a 80ºC, com
ϕ
constante e igual a 65%. A
umidade relativa foi incrementada de 1% entre 66 e 85% com temperatura constante de
40ºC. Os gráficos 2.3-1 a 2.3-4 apresentam os resultados desse estudo2 de sensibilidade.
2
O estudo em questão compara as sensibilidades de pasta rica em fibras, com
pasta isenta de fibras, que é o produto, usualmente consumido, objeto deste trabalho.
33
SENSIBILIDADE RELATIVA
RICO EM FIBRAS
SEM FIBRAS
TEMPERATURA (ºC)
Gráfico
2.3-1
-
Efeito
da
temperatura
na
difusividade
efetiva
(VILLENEUVE e GÉLINAS 2006)
SENSIBILIDADE RELATIVA
RICO EM FIBRAS
SEM FIBRAS
UMIDADE RELATIVA (%)
Gráfico 2.3-2 - Efeito da umidade relativa na difusividade efetiva
SENSIBILIDADE RELATIVA
(VILLENEUVE e GÉLINAS 2006)
SEM FIBRAS
RICO EM FIBRAS
TEMPERATURA (ºC)
34
Gráfico 2.3-3 - Efeito da temperatura na umidade de equilibrio
(VILLENEUVE e GÉLINAS 2006)
SENSIBILIDADE RELATIVA
RICO EM FIBRAS
SEM FIBRAS
UMIDADE RELATIVA (%)
Gráfico 2.3-4 -Efeito da umidade relativa na umidade de equilíbrio
(VILLENEUVE e GÉLINAS 2006)
A análise de sensibilidade mostra que o efeito da umidade relativa é maior que o
efeito da temperatura, tanto na difusividade efetiva como na umidade de equilíbrio.
Mostra também que a variação de ambas as propriedades é relativamente pequena
mesmo em intervalos grandes, tanto de temperatura como de umidade relativa.
Derivando a equação 2.3-3 em relação ao tempo, para intervalos de
X para os
quais a difusividade efetiva ( D ) possa ser considerada como constante, chega-se a uma
expressão importante para o estabelecimento de um modelo de controle do processo de
secagem.
 β 2 Dt   dX
4
dX 
D
= 1 − 2 exp  − 1 2   e − β 2 2 ( X − X e )


dt  β1
Rp
 R p   dt
2.3-5
Se além da difusividade efetiva, também a umidade de equilíbrio puder ser
considerada constante, tem-se:
dX
D
= − β12 2 ( X − X e )
dt
Rp
2.3-6
A pasta longa existe em duas formas, espaguete e talharim, a equação que
descreve a umidade média da pasta para o talharim, obtida da aplicação da Lei de Fick
para uma placa plana, estabelecida por ANDRIEU e STAMATOPOULOS (1986), é
semelhante na forma à equação 2.3-3:
35
 π 2 Dt 
X − Xe
8
= 2 exp  −
2 
X0 − Xe π
 4 L 
2.3-7
na qual L é metade da espessura do talharim.
Devido a esta semelhança entre as expressões, o modelo desenvolvido para o
espaguete também é aplicável ao talharim.
Estas relações foram desenvolvidas para a variação da umidade média de uma
quantidade definida de pasta, sendo, portanto, aplicáveis na forma como foram
desenvolvidas
para
processos
em
batelada
(secagem
sob
condições
externas
constantes).
Os secadores atualmente usados na indústria são do tipo contínuo, ou seja o
macarrão, imediatamente após extrudado atravessa uma sequência de células (ou
câmaras) e sai na umidade desejada no final da linha.
2.4.
SECAGEM CONTÍNUA
As relações obtidas para secagem em batelada foram adaptadas para uso em
processo de secagem contínuo, por KÜÇÜK e ÖZILGEN (1997), utilizando expressões
para o cálculo da umidade de equilíbrio (Xe) e a difusividade (D), corrigidas para minimizar
o erro que aparece ao usar esses parâmetros obtidos em secagem em bateladas e em
escala de laboratório.
Conforme KÜÇÜK e ÖZILGEN (1997), no projeto de um processo de secagem,
usualmente são obtidos dados experimentais com equipamento de laboratório, que são
usados para projetar uma planta piloto, em escala. Os testes realizados na planta piloto
ajudam a fazer as correções finais nos dados para o projeto do equipamento em escala
industrial. Os experimentos com a planta piloto podem ser omitidos devido e seu custo
elevado (KÜÇÜK e ÖZILGEN citando BISIO (1985)). Dessa forma, os resultados obtidos
com a unidade industrial usualmente diferem da expectativa baseada nos dados obtidos
em laboratório. O projeto será considerado bem sucedido se as diferenças entre os
objetivos do projeto e o desempenho efetivo do equipamento industrial ficarem dentro de
limites aceitáveis.
36
Comparando dados de umidade efetiva de espaguete ao sair de um secador
industrial com a umidade calculada pelas equações 2.3-1 e 2.3-3 (ANDRIEU e
STAMATOPOULOS (1986)) usando dados obtidos em um secador de laboratório do tipo
batelada, KÜÇÜK e ÖZILGEN (1997) estabeleceram uma forma de corrigir as expressões
válidas para secagem em batelada de maneira a poderem ser usadas para processos de
secagem contínua.
A expressão proposta para o cálculo da umidade de equilíbrio
 ϕ 
X e = (1 + ξ ) (0,154 − 1, 22 ×10 × T ) 

 1−ϕ 
X e é:
( 0,078+ 7,32×10
−3
×T
)
−3
Na qual
ϕ
2.4-1
é a umidade relativa do ar úmido que envolve o macarrão e
T é a
temperatura em graus Celsius.
O fator de correção
ξ
X e para uma
aumenta o valor da umidade de equilíbrio
dada condição de umidade e temperatura. Para manter o valor adequado de
obtenção de uma umidade final desejada
X e para
X da pasta torna-se necessário estabelecer
uma condição de umidade relativa mais baixa, o que obriga a uma vazão maior de ar
externo admitido na célula.
Uma
possível
explicação para
essa
condição de
operação
é
a
falta
de
homogeneidade no fluxo de ar no entorno de cada fio de macarrão. Nos fios envoltos por
um fluxo de ar menor a umidade relativa deve ser mais baixa para provocar o remoção
de umidade da pasta desejada.
O processo de secagem de macarrão é controlado pelas condições internas, com a
taxa de secagem decrescendo à medida que a umidade média da pasta se aproxima da
umidade de equilíbrio. Existem dois períodos distintos, chamados de primeiro e segundo
períodos de taxa decrescente.
No primeiro período de taxa decrescente há umidade na superfície e a taxa de
migração de água do interior para a superfície do macarrão é menor do que a taxa de
evaporação da água na superfície. No segundo período de taxa decrescente não há mais
umidade na superfície do macarrão e a superfície líquida da água está nos capilares e se
aprofunda à medida que a secagem prossegue, a evaporação ocorre abaixo da superfície
da pasta, e a difusão do vapor ocorre desde o ponto de evaporação até a superfície.
37
KÜÇÜK
difusividade
e
ÖZILGEN
(1997)
propuseram
uma
expressão
para
cálculo
da
D em cada um dos períodos. As expressões são:
ln D1 = ln(1 − ξ ) − (20,1 − 0.086ϕ ) −
1378 + 24, 6ϕ
T
2.4-2
1705 + 19, 6ϕ
T
2.4-3
ln D2 = ln(1 − ξ ) − (20,3 − 0.075ϕ ) −
Por um processo de tentativa e erro, o valor ótimo calculado para o fator de
correção
2.5.
ξ
foi 0,2.
A QUESTÃO DO CONTROLE
O objetivo deste trabalho é modelar o processo de secagem de macarrão de forma
a que o modelo obtido se preste para o projeto de um controlador para o secador. É
então necessário escolher um método de controle para definir a forma adequada de
construir o modelo.
2.5.1. Teoria de controle moderno
Segundo FRIEDLAND (2005), a definição do processo de controle é o terceiro e
final estágio do desenvolvimento do sistema de controle, o estágio no qual as
características dinâmicas do compensador são conhecidas, depois que o conceito de
controle tenha sido estabelecido, depois que o hardware (sensores e atuadores) tenham
sido selecionados, depois que o desempenho necessário tenha sido determinado.
Ainda conforme FRIEDLAND (2005) este aspecto da engenharia de sistema de
controle é geralmente chamado “teoria”. O termo “teoria” é adequado por várias razões.
Primeiro
porque
é
essencialmente
matemático
no
conteúdo,
e
matemática
é
frequentemente equiparada a teoria. Segundo porque trata não com os dispositivos
reais, mas com seus modelos (teóricos, isto é, matemáticos) idealizados. Terceiro, ele
constitui um corpo sistemático de conhecimentos: teoremas, algoritmos de projeto,
métodos gráficos, e outros que possam ser aplicados em controles de sistemas
independente da tecnologia específica usada na sua implementação.
38
A história da teoria de controle pode ser convenientemente dividida em três
períodos. O primeiro, começando na pré-história e terminando no início da década de 40,
pode ser chamado de período primitivo. Ele foi seguido por um período clássico, que mal
durou 20 anos, e finalmente veio o período moderno.
O termo primitivo é usado aqui não com um sentido pejorativo, mas no sentido de
que a teoria consistia em um conjunto de análises de processos específicos, por métodos
matemáticos apropriados, e frequentemente inventados para lidar com eles, em vez de
um corpo organizado de conhecimentos que é o que caracteriza os períodos clássico e
moderno.
Embora os princípios de feedback possam ser encontrados na tecnologia da Idade
Média e anterior, o uso intencional do feedback para melhorar o desempenho de
sistemas dinâmicos começou por volta do começo da revolução industrial no final do
século 18, início do 19. O marco foi o controlador centrífugo inventado por James Watt
para controlar a velocidade de sua máquina a vapor. Ao longo da primeira metade do
século 19, engenheiros e “mecânicos” inventaram outros tipos de controladores de
melhor desempenho. Os princípios teóricos que descrevem a operação dos controladores
foram estudados por grandes físicos dos séculos 18 e 19, como Huygens, Hooke, Airy e
Maxwell. Pela metade do século 19 sabia-se que a estabilidade de um sistema dinâmico
era determinada pela localização das raízes da equação característica.
Os problemas matemáticos que surgiram na estabilidade de sistemas de controle
realimentados ocuparam a atenção de matemáticos do inicio do século 19.
O período clássico da teoria de controle começou durante a Segunda Guerra
Mundial no Laboratório de Radiologia do MIT. Estava a cargo do pessoal do Laboratório
de Radiologia, que incluía engenheiros, físicos e matemáticos, a solução de problemas de
engenharia que apareceram devido ao esforço de guerra, incluindo sistemas de controle
de radar e de controle de tiro. O laboratório que estava encarregado dos problemas em
sistemas de controle incluía tanto pesquisadores familiarizados com os métodos de
resposta em frequência desenvolvidos por Nyquist e Bode para sistemas de comunicação,
como engenheiros com conhecimentos de outras técnicas. Trabalhando juntos, eles
desenvolveram uma teoria de controle sistemática que não era ligada a nenhuma
aplicação em particular.
39
O uso dos métodos no domínio da frequência (transformada de Laplace) tornou
possível a representação de um processo por sua função de transferência e assim
permitiram a visualização da interação dos vários subsistemas de um sistema complexo
pela interligação das funções de transferência no diagrama de blocos. O diagrama de
blocos contribuiu talvez tanto quanto qualquer outro fator para o desenvolvimento da
teoria de controle como uma disciplina distinta. Com seu uso é possível estudar o
comportamento dinâmico de um sistema hipotético manipulando e combinando “caixas
pretas” no diagrama de blocos sem ter que conhecer o que acontece dentro das “caixas
pretas”.
O período clássico da teoria de controle, caracterizado pela análise no domínio da
frequência, continua em vigor, agora em uma fase “neoclássica” com o desenvolvimento
de varias técnicas sofisticadas para sistemas multivariáveis. Mas há concomitante com
ele o período moderno que começou no fim da década de 50, início de 60.
Os métodos do espaço dos estados são a pedra fundamental da teoria de controle
moderno.
A
característica
essencial
dos
métodos
do
espaço
dos
estados
é
a
representação dos processos por meio de equações diferenciais em lugar de funções de
transferência. Isto pode, à primeira vista, parecer um retrocesso ao primeiro período, no
qual as equações diferenciais também eram usadas para representar o comportamento
dinâmico dos processos. Mas naquele período os processos eram suficientemente simples
para poderem ser representados por uma só equação de ordem razoavelmente baixa. No
enfoque moderno os processos são modelados por sistemas de equações de primeira
ordem. Em princípio não há limite para o número de equações de primeira ordem do
sistema. Na prática a única limitação está na capacidade de o software processar os
cálculos necessários com confiabilidade.
2.5.2. Escolha
O equipamento de secagem, conforme descrito em 2.1, é composto de muitas
células interligadas, porém com controle independente, tendo cada célula vários
parâmetros para ser controlados, de forma que resultam em uma quantidade grande de
variáveis para controlar.
2.6.
MODELAGEM
A descrição de um processo no espaço dos estados requer sua representação por
um conjunto de vetores que representem as entradas, o estado e as saídas do sistema.
40
Entradas são as variáveis manipuladas intencionalmente para operação do
sistema de controle.
O estado do sistema é representado por um conjunto de variáveis, chamadas
variáveis de estado, que permitam o conhecimento completo do sistema em qualquer
dado momento.
Saídas são variáveis que podem ser medidas através de sensores adequados.
Tomando a dinâmica do sistema descrita por um conjunto de equações como
segue:
dx1
= f1 ( x1 , x2 ,..., xk , u1 , u2 ,..., ul , t )
dt
dx2
= f 2 ( x1 , x2 ,..., xk , u1 , u2 ,..., ul , t )
dt
................................................................
2.6-1
dxk
= f k ( x1 , x2 ,..., xk , u1 , u2 ,..., ul , t )
dt
na qual x1, x2,
...xk são variáveis de estado, u1, u2, ...ul são entradas do sistema, também
chamadas de variáveis de controle.
A modelagem objetivada por este trabalho apresentará a variação no tempo de
cada variável de estado do processo de secagem contínua de macarrão em função das
outras variáveis de estado.
41
3. METODOLOGIA
A metodologia usada neste trabalho está ilustrada no diagrama abaixo:
PESQUISA BIBLIOGRÁFICA
ESCOLHA DE UMA ISOTERMA
CONFORME ESTUDOS
PESQUISADOS
COMPARAÇÃO DA CURVA OBTIDA
COM A CURVA DE SECAGEM DE
UM SECADOR INDUSTRIAL
CONCLUSÃO
DEFINIÇÃO DE UM TIPO DE
SECADOR PARA SERVIR DE BASE
PARA A MODELAGEM DO
PROCESSO DE SECAGEM
MODELAGEM DO PROCESSO DE
SECAGEM
42
PROJETO BÁSICO DE UM
SECADOR PARA SERVIR DE BASE
PARA A SIMULAÇÃO
CONSTRUÇÃO DO MODELO NO
“SIMULINK” (MÓDULO DE
SIMULAÇÃO DO SOFTWARE
MATLAB)
SIMULAÇÕES
CONCLUSÕES
3.1.
DESCRIÇÃO
A pesquisa bibliográfica forneceu três modelos de isotermas para a secagem de
macarrão, são os modelos desenvolvidos por ANDRIEU et al. (1985), VILLENEUVE e
GÉLINAS (2006) e KÜÇÜK e ÖZILGEN (1997).
Dos três modelos para isoterma de secagem de espaguete estudados, o único que
propõe uma adequação do modelo obtido em laboratório, por análise de uma secagem
em batelada, para uso em secador contínuo industrial, é o modelo proposto por KÜÇÜK e
ÖZILGEN (1997), de forma que optou-se por usá-lo na modelagem de um secador
industrial, proposta neste trabalho.
Buscando validar a escolha feita, procurou-se comparar o desempenho de um
secador real com o desempenho do processo de secagem proposto por KÜÇÜK e
ÖZILGEN (1997).
43
O catálogo para linha de produção de pasta longa de Pavan S. p. A., acessível em
http://www.pavan.com/catalogues.asp, apresenta o desempenho do secador através das
curvas de evolução da umidade da pasta, umidade relativa e temperatura internas do
secador em função do tempo de secagem (tempo de permanência da pasta ao longo do
secador), conforme a figura 3.1-1.
Figura 3.1-1 – Curva de secagem (catálogo Pavan S.p.A.,2007)
A imagem foi ampliada para aumentar a precisão de leitura e os valores de
umidade da pasta
X , temperatura T e umidade relativa ϕ foram tabelados para melhor
visualização conforme tabela 3.1-1. As três primeiras linhas correspondem à fase de présecagem.
44
Tabela 3.1-1 – Processo de secagem do secador Pavan
Para
a
Tempo
de
secagem
(horas)
X
(%)
T
(ºC)
(%)
0,5
0,75
1
30
22
17,6
55
75
98
85
85
85
1,75
2,5
3,25
4
4,75
5,5
16
14,3
14
13,6
14,3
14,3
90
90
85
85
70
70
80
80
80
80
73
82
comparação
procurou-se,
usando
ϕ
o
modelo
escolhido
(KÜÇÜK
e
ÖZILGEN, 1997), estabelecer qual a umidade relativa, necessária para levar a pasta á
mesma umidade e temperatura do secador real, em cada fase do processo.
A comparação feita foi, então, entre a umidade relativa real e a calculada pelo
modelo proposto, para cada fase do processo.
Para o cálculo da umidade relativa, calculou-se, inicialmente, a umidade de
equilíbrio
X e , necessária para levar a umidade da pasta ao valor desejado após o tempo
de percurso do macarrão no secador, em cada fase do processo de secagem.
Esse cálculo foi feito usando-se a equação 2.3-3, que relaciona a umidade média
da pasta
X , após o tempo de percurso dentro de uma célula do secador, com a umidade
média inicial
X 0 e a umidade de equilíbrio X e .
A umidade média inicial
X 0 , a umidade média X e o tempo de percurso, foram
retirados do catalogo citado. A umidade inicial é de 43%, base seca, a umidade
Xe o
tempo de percurso estão na tabela 3.1-1 para cada fase da secagem.
45
Usou-se o fator
β1
R p = 0,85 x 10-3m (espaguete de 1,7mm de
= 2,4048,
diâmetro) e os valores da difusividade efetiva
D , calculados pelas equações 2.3-2 e 2.3-
3, (KÜÇÜK e ÖZILGEN, 1997). Para o cálculo da difusividade
D foram usados os valores
da temperatura e da umidade relativa da tabela 3.1-1.
A seguir, com a temperatura
T da tabela 3.1-1 e a umidade de equilíbrio
calculada como exposto, calculou-se a umidade relativa
secagem, usando a equação 2.3-1, com fator
ξ
ϕ
para cada fase do processo de
= 0,2 (KÜÇÜK e ÖZILGEN, 1997).
As umidades relativas assim obtidas foram comparadas com a umidade declarada
no catálogo Pavan.
Analisaram-se as diferenças entre os valores de catálogo e os calculados, em cada
fase do processo, da seguinte forma:
Para cada fase do processo calculou-se a diferença, em valor absoluto, entre o
valor de catálogo da umidade relativa e o valor calculado para o modelo de isoterma.
Calculou-se, então, a diferença percentual média. A tabela 3.1-2 mostra o resumo deste
procedimento de análise.
Tabela 3.1-2 – Comparação de modelos de isoterma.
Pavan
Küçük e Özilgen
Tempo de
secagem
(horas)
0,5
0,75
1
X
(%)
T
(ºC)
ϕ
ϕ
(%)
(%)
Diferença
percentual
30
22
17,6
55
75
98
85
85
85
73,4
67,1
80,3
13,6
21,1
5,5
1,75
2,5
3,25
4
4,75
5,5
16
14,3
14
13,6
14,3
14,3
90
90
85
85
70
70
80
80
80
80
73
82
80,6
75,9
76,8
76,1
71,8
71,8
0,7
5,1
4,0
4,9
1,6
12,4
Diferença percentual média
7,7
46
Como pode-se observar na tabela 3.1-2 a diferença percentual média, entre o
valor calculado e o de catálogo é de 7,7%. Levando em consideração que o gráfico de
catálogo é informação comercial, sem precisão portanto, porém real (por uma questão de
idoneidade e ética do fabricante em questão), a diferença mostra que há coerência entre
os resultados obtidos pelo modelo considerado e o desempenho real de um secador
industrial, validando assim a escolha feita.
47
4. DEFINIÇÃO DE UM TIPO DE SECADOR
4.1.
DESCRIÇÃO
A modelagem está ligada a um determinado tipo de secador, apresentando
diferenças nas equações obtidas para descrever o processo de secagem. Entre os
diversos tipos examinados, conforme descrito no item 1.3, optou-se por um secador
semelhante ao Braibanti da figura 1.3-7, com algumas modificações. Na região de présecagem os ventiladores de circulação do ar úmido da célula são colocados abaixo do
trocador de calor, como observado em linha de secagem de um pastifício visitado.
Na região da secagem final, optou-se pelo uso de três planos independentes,
como no secador Pavan, ilustrado na figura 1.3-8, porém mantendo a configuração das
células da pré-secagem, com os ventiladores abaixo do trocador de calor, como mostrado
no corte transversal esquemático da figura 4.1-1
m ar s
Pvent
T
m ar e
T0
Patm
TE
TT
m ar v
T
Figura 4.1-1 – Corte transversal do secador proposto para modelagem
48
Cada célula é constituída de um leito para a passagem das barras, carregadas
com o espaguete, que cruzam longitudinalmente o secador. Acima do leito de pasta fica
um trocador de calor aquecido com água quente. Entre o trocador de calor e o leito de
pasta estão instalados dois ventiladores axiais para prover a circulação do ar.
Acima do trocador de calor está o duto de alimentação de ar externo, provido de
um damper para controle da vazão de ar.
Nas laterais do teto do secador estão tomadas de ar de exaustão, uma de cada
lado, ambas estão conectadas na sucção de um ventilador centrífugo.
O fluxo de ar, conforme indicado pelas setas, na figura 4.1-1, é descendente na
parte central da célula, onde o ar externo admitido passa pelo trocador de calor e
atravessa o leito de pasta, sendo então desviado, por chapas curvas, para as laterais. O
fluxo de ar em ambas laterais é ascendente e não se mistura com o descendente devido
a duas paredes, uma em cada lateral do leito de pasta.
Próximo ao teto, em cada lateral, o fluxo ascendente divide-se em dois, um de
menor vazão sai pelo duto de exaustão e o remanescente, de maior vazão, é desviado,
por chapas curvas, para a região acima do trocador de calor, misturando-se com o ar
externo admitido pelo duto com damper.
49
5. MODELAGEM
A forma escolhida para a modelagem da dinâmica do secador foi a de apresentar
a variação de cada variável de estado em função das variáveis de estado e das entradas
do sistema.
As variáveis de estado do sistema de secagem são:
−
T - temperatura média do ar na célula
−
P - pressão do ar na célula
−
ω
−
TaqS - temperatura de saída da água quente
- umidade absoluta média do ar na célula
As entradas do sistema, que são as variáveis possíveis de ser controladas, para
operação dentro do processo especificado, são:
5.1.
−
m& ge - vazão de ar seco admitido no secador
−
m& aq - vazão de água quente no trocador de calor
TEMPERATURA
Escrevendo o balanço de energia para um volume de controle (também referido
neste texto como VC) que contenha o ar dentro da célula, mas exclua a pasta e o
trocador de calor, tem-se:
d
& −∑ mh
&
Q& liq =
∫ u ρ dV + ∑s mh
dt VC
e
5.1-1
50
na qual:
Q& liq = Q& Trocado com trocador de calor − Q& Trocado com apasta
d
∫ u ρ dV = variação de energia interna da massa de ar úmido no VC
dt VC
& − ∑ mh
& = energia transportada pelos fluxos de ar úmido entrando
∑ mh
s
e
e saindo do VC e fluxo de água trocado com a pasta
Hipóteses feitas no modelo adotado:
O ar úmido dentro das células é retirado por meio de ventiladores centrífugos cuja
vazão é controlada por meio de dampers, ficando, portanto a pressão ligeiramente
abaixo da atmosférica (cerca de 91.300 a 96.300 Pa). A temperatura varia de célula para
célula, ao longo do processo, no intervalo de 50ºC a 110ºC. É portanto possível tratá-lo
como uma mistura de gases ideais.
A variação máxima de temperatura que a mistura sofre é inferior a 100ºC (varia
de temperatura ambiente a 110ºC), a variação do calor específico a volume constante,
cv e calor específico a pressão constante cp , neste intervalo é da ordem de 1%, de
forma que, neste estudo, ambos serão admitidos constantes.
5.1.1. Variação da energia interna da massa de ar úmido no VC
d
d
d
u ρ dV = ( µar umido M ar umido ) = ( ug M g + u A M A )
∫
dt VC
dt
dt
5.1-2
na qual:
−
u g = energia interna média do ar seco contido na celula;
−
uA
−
M g = massa de ar seco contido na célula;
−
M A = massa de vapor de água contido no ar dentro da célula.
= energia interna média do vapor de água contido na célula;
51
du g
dM g
d
du
dM A
ug M g + u A M A ) = M g
+ ug
+ M A A + uA
(
dt
dt
dt
dt
dt
dM g
dt
= m& ge − m& gs
5.1-3
5.1-4
na qual:
−
m& ge = vazão mássica do ar, em base seca, que entra no volume de controle;
−
m& gs = vazão mássica do ar, em base seca, que sai do volume de controle;
dM A
= m& Ae + m& AP − m& As
dt
5.1-5
na qual:
−
m& Ae = vazão mássica de vapor de água contido no ar que entra no volume de
controle;
−
m& AP = vazão mássica do vapor de água, trocado pela pasta, que entra no volume
de controle;
−
m& As = vazão mássica de vapor de água contido no ar que entra no volume de
controle;
Substituindo 5.1-5 e 5.1-4 em 5.1-3; e 5.1-3 em 5.1-2, tem-se:
du g
d
du
+ u g ( m& ge − m& gs ) + M A A + u A ( m& Ae + m& AP − m& As )
u ρ dV = M g
∫
dt VC
dt
dt
5.1-6
5.1.2. Energia transportada pelos fluxos de massa entrando e saindo do
VC
& −∑ mh
& = ( m&
∑ mh
gs
s
h gs + m& As h As ) − ( m& ge h ge + m& Ae h Ae + m& AP h AP )
5.1-7
e
52
na qual:
−
h ge = entalpia do ar seco que entra no volume de controle;
−
h gs = entalpia do ar seco de sai do volume de controle;
−
h Ae = entalpia do vapor de água, contido no ar, que entra no volume de controle;
−
h As = entalpia do vapor de água, contido no ar, que sai do volume de controle
−
h AP = entalpia do vapor de água trocado com a pasta;
Considerando que o ar úmido que sai do volume de controle tem as mesmas
propriedades médias que o ar úmido no interior da célula, devido à intensa agitação do
ar provocada pelos ventiladores de circulação, vem:
hgs = hg
5.1-8
hAs = hA
5.1-9
e
nas quais:
−
hg = entalpia média do ar seco no interior da célula;
−
hA = entalpia média do vapor de água no interior da célula;
Conforme WAANANEM e OKOS (1994), a secagem do macarrão pode ser admitida
como um processo isotérmico, o processo de troca de calor com a pasta é muito mais
rápido que o processo de troca de massa. A pasta permanece tempo bastante longo (20
a 45 min) dentro de cada célula para atingir o teor de umidade programado para aquela
fase do processo de secagem, porém logo nos primeiros minutos atinge temperatura
muito próxima da temperatura do ar úmido. A pasta atinge valores de temperatura entre
a temperatura de bulbo seco e a de bulbo úmido. Para efeito deste estudo vamos admitir
que a temperatura média da pasta seja igual à temperatura média do ar úmido, então:
hAP = hA
5.1-10
Substituindo 5.1-8, 5.1-9 e 5.1-10 em 5.7-7, fica:
53
& −∑ mh
& = ( m&
∑ mh
h + m& As hA ) − ( m& ge h ge + m& Ae h Ae + m& AP hA )
gs g
s
5.1-11
e
5.1.3. Balanço de energia no VC
Substituindo 5.1-6 e 5.1-11 em 5.1-1, chega-se a:
du g
du
Q& liq = M g
+ u g ( m& ge − m& gs ) + M A A + u A ( m& Ae + m& AP − m& As ) +
dt
dt
( m& gs hg + m& As hA ) − ( m& ge h ge +m& Ae h Ae +m& AP hA )
5.1-12
Substituindo,
u g = hg − Pg vg = hg − Rg T
5.1-13
u A = hA − PAv A = hA − RAT
5.1-14
Vem:
du g
du
Q& liq = M g
+ M A A + ( hg − Rg T ) ( m& ge − m& gs ) + ( hA − RAT ) ( m& Ae + m& AP − m& As ) +
dt
dt
( m& gs hgs + m& As hAs ) − ( m& ge hge + m& Ae hAe + m& AP hA )
5.1-15
Cancelando os termos semelhantes e com sinal oposto, e substituindo:
hg − hge = cpg (T − T0 )
5.1-16
hA − hAe = cp A (T − T0 )
5.1-17
m& Ae = ω0 m& ge
5.1-18
m& As = ω m& gs
5.1-19
du g = cvg dT
5.1-20
du A = cv A dT
5.1-21
Tem-se:
54
dT
Q& liq = M g ( cvg + ω cv A )
+ m& gs ( Rg + ω RA ) T + m& ge (T − T0 ) ( cpg + ω0 cp A ) −
dt
m& ge ( Rg + ω0 RA ) T − m& AP RAT
5.1-22
na qual:
−
cvg = calor específico a volume constante do ar seco contido na célula;
−
cv A = calor específico a volume constante do vapor de água contido no ar úmido
da célula;
−
cpg = calor específico a pressão constante do ar seco contido na célula;
−
cp A = calor específico a pressão constante do vapor de água contido no ar úmido
da célula;
−
ω0
−
ω
−
T0 =temperatura (de bulbo seco) do ar ambiente (externo ao secador);
−
T =temperatura (de bulbo seco) do ar dentro da célula;
= umidade absoluta do ar ambiente (externo ao secador);
= umidade absoluta do ar dentro da célula;
Para simplificar a notação, considerando:
cvg + ω cv A = cvar
5.1-23
Rg + ω RA = Rar
5.1-24
cp g + ω0 cp A = cp0 ar
5.1-25
Rg + ω0 RA = R0 ar
5.1-26
nas quais:
−
cvar = calor específico a volume constante, do ar úmido, à temperatura T,
referido à massa de ar seco;
−
Rar = constante de gás ideal do ar, dentro da célula, referida à massa de ar seco;
−
cp0 ar = calor específico a pressão constante, do ar úmido, à temperatura T0,
referido à massa de ar seco;
−
R0 ar = constante de gás ideal do ar ambiente, referida à massa de ar seco;
55
E substituindo 5.1-23 a 5.1-26 em 5.1-22, obtém-se:
M g cvar
dT &
= Qliq − m& gs RarT − m& ge cp0 ar (T − T0 ) + m& ge R0 arT + m& AP RAT
dt
5.1-27
5.1.4. Calor líquido trocado
Q& liq = Q&TC + Q& PASTA
5.1-28
na qual:
−
Q& liq = fluxo de calor através da fronteira do volume de controle (VC);
−
Q&TC = fluxo de calor trocado com o trocador de calor (TC);
−
Q& PASTA = fluxo de calor trocado com a pasta
5.1.4.1.
Tomando
CALOR TROCADO COM A PASTA
um
VC
contendo
o
leito
de
pasta
que
atravessa
a
célula
longitudinalmente, conforme mostrado na figura 5.1-1, excluindo o ar úmido da célula,
tem-se:
m AP
m p (1+x0 )
m p (1+x )
Figura 5.1-1 – VC contendo a pasta dentro da célula
56
Neste texto, quando mencionado umidade inicial da pasta
X 0 , ou umidade final
X , entende-se o valor médio para cada cilindro de espaguete, obtido pela integração da
distribuição de umidade ao longo do raio do cilindro, uma vez que, na fase de
resfriamento, logo após a secagem, a umidade vai homogeneizar-se em todo o volume
do cilindro com o valor médio final do processo de secagem.
Balanço de massa no VC:
m& P (1 + X 0 ) = m& P (1 + X ) + m& AP
5.1-29
na qual:
−
m& P = vazão de pasta base seca;
−
X 0 = umidade inicial da pasta ao entrar na célula;
−
X = umidade final da pasta ao sair da célula;
−
m& AP = umidade trocada entre a pasta e o ar do interior da célula;
Efetuando os parênteses e simplificando, vem:
m& AP = m& P ( X 0 − X )
5.1-30
Balanço de energia no VC:
Conforme WAANANEN e OKOS (1994), o processo de troca de calor é muito mais
rápido que o processo de troca de massa, e isso se deve, principalmente, ao baixo calor
específico da pasta (da ordem de 1 a 1,5 kJ/kgK). Assim, nos primeiros minutos, ao
entrar na célula, a pasta atinge a temperatura do ar úmido, e a energia necessária para
isso é muito baixa (da ordem de 4% da energia trocada pelo trocador de calor), de forma
que será desconsiderada.
Q& PASTA =  m& P hP + Xm& P hAl + ( X 0 − X ) m& P hAv  − ( m& P hP 0 + X 0 m& P hAl )
5.1-31
na qual:
57
−
hP = entalpia do macarrão ao sair da célula;
−
hP 0 = entalpia do macarrão ao entrar na célula;
−
hAl = entalpia da água (líquido saturado);
−
hAv = entalpia da água (vapor saturado);
Efetuando os parênteses, e substituindo 5.1-30 em 5.1-31, vem:
Q& PASTA = m& P ( hP − hP 0 ) + m& AP ( hAv − hAl )
5.1-32
Considerando a temperatura de entrada da pasta igual à temperatura de saída e
igual à temperatura média do ar úmido, vem:
m& P ( hP − hP 0 ) = m& P cpPASTA (Ts − Te ) = 0
5.1-33
A equação 5.1-32 fica:
Q& PASTA = m& AP ( hAv − hAl ) = m& AP hA lv
5.1-34
na qual:
−
hA lv = entalpia de evaporação da água, à temperatura do ar úmido da célula.
5.1.4.2.
CALOR TROCADO COM O TROCADOR DE CALOR
Tomando um volume de controle em torno do ar contido no trocador de calor (VC
engloba só o ar úmido).
Balanço de energia:
d
Q&TC = ( uar M ar ) + m& gs TC hgs TC − m& ge TC hge TC + m& As TC hAs TC − m& Ae TC hAe TC
dt
(
) (
)
5.1-35
na qual:
58
−
uar = energia interna do ar no VC;
−
M ar = massa de ar úmido no VC;
−
m& gs TC = vazão mássica de ar seco, saindo do VC;
−
m& ge TC = vazão mássica de ar seco, entrando no VC;
−
m& As TC = vazão mássica de vapor de água contido no ar saindo do VC;
−
m& Ae TC = vazão mássica de vapor de água contido no ar entrando no VC;
−
hgs TC = entalpia do ar seco, saindo do VC;
−
hge TC = entalpia do ar seco, entrando no VC;
−
hAs TC = entalpia do vapor de água contido no ar úmido saindo do VC;
−
hAe TC = entalpia do vapor de água contido no ar úmido entrando no VC;
A massa de ar
M ar , contida no VC, é muito pequena (para um trocador de calor
do tipo compacto, com 2 m x 0,5 m x 0.2 m, é de cerca de 0.15 kg), comparada à massa
total de ar dentro da célula (cerca de 30 kg) e a massa de metal e de água quente do
trocador de calor ( cerca de 20 kg e 15 kg respectivamente), portanto sua capacidade
térmica pode ser desprezada e, em consequência o acúmulo de energia também não é
significativo.
A vazão de ar úmido deixando o trocador de calor pode ser admitida igual à vazão
do ar que entra, pois o ar a baixas velocidades pode ser considerado incompressível.
Como não há perda ou adição de vapor de água dentro do VC, resulta que a vazão
mássica do vapor de água contido no ar úmido na saída é igual à vazão da entrada,
então:
m& gs TC = m& ge TC = m& g TC
5.1-36
m& As TC = m& Ae TC = m& A TC
5.1-37
e
nas quais:
−
m& g TC = vazão de ar seco através do trocador de calor;
−
m& A TC = vazão de vapor de água contido no ar úmido através do trocador de calor.
59
Com essas considerações a equação 5.1-35 fica:
(
)
(
Q&TC = m& g TC hgs TC − hge TC + m& A TC hAs TC − hAe TC
)
5.1-38
Considerando:
m& A TC = ωE m& g TC
5.1-39
hgs TC − hge TC = cpg (TT − TE )
5.1-40
hAs TC − hAe TC = cp A (TT − TE )
5.1-41
nas quais:
−
TT = temperatura de saída do trocador de calor, do ar úmido;
−
TE = temperatura de entrada no trocador de calor, do ar úmido
Substituindo 5.1-39 a 5.1-41 em 5.1-38, vem:
Q&TC = m& g TC ( cpg + ωE cp A ) (TT − TE )
5.1-42
cp g + ωE cp A = cpar TE
5.1-43
Considerando:
Para facilitar a notação, substituindo 5.1-43 em 5.1-42, tem-se:
Q&TC = m& g TC cpar TE (TT − TE )
5.1.4.3.
5.1-44
CALOR LÍQUIDO TROCADO
Substituindo 5.1-34 e 5.1-44 em 5.1-28, tem-se o calor líquido trocado com o ar
úmido dentro da célula:
60
Q& liq = m& g TC cpar TE (TT − TE ) − m& AP hA lv
O sinal negativo para o termo
5.1-45
Q& PASTA deve-se ao fato de que o fluxo de calor
trocado com a pasta sai do VC em torno do ar úmido no interior da célula.
5.1.5. Temperatura TE de entrada no trocador de calor
Tomando um volume de controle que contenha a massa de ar na entrada do
trocador de calor, compreendendo a região onde o fluxo de ar externo admitido
encontra-se com os fluxos de ar interno recirculado, conforme mostra a figura 5.1-2.
m ar s= m gs (1+w)
m ar e= m ge (1+w0 )
m ar TC= m g TC (1+wE )
m ar v = m gv (1+w)
Figura 5.1-2 – VC na região da mistura do ar admitido com o recirculado
Balanço de energia:
d
& − ∑ mh
&
Q& liq =
∫ u ρ dv + ∑S mh
dt VC
E
Q& liq = 0
5.1-46
não há fonte de calor no VC
dM ar
du
d
d
u ρ dv = (uar M ar ) = uar
+ M ar ar
∫
dt VC
dt
dt
dt
5.1-47
61
na qual:
−
M ar = massa de ar úmido no VC;
−
uar = energia interna média do ar no VC.
Considerando que:
M ar
duar
dT
= M ar cvar E
1
4
24
3
dt
dt
5.1-48
a TE e ω E
uar = har TE − Rar TETE
5.1-49
dM ar
= m& ar e + (m& ar v − m& ar s ) − m& arTC
dt
5.1-50
nas quais:
−
cvar = calor específico a volume constante do ar úmido no VC;
−
TE = temperatura do ar úmido na saída do VC (e entrada no trocador de calor);
−
har TE = entalpia média do ar úmido no VC;
−
Rar TE = constante de gás ideal do ar úmido no VC;
−
mar e = vazão mássica de ar úmido admitido na célula;
−
mar v = vazão mássica dos ventiladores de circulação (total);
−
mar s = vazão mássica de ar úmido saindo da célula;
−
marTC = vazão mássica de ar úmido através do trocador de calor.
Substituindo 5.1-48 a 5.1-50 em 5.1-47, tem-se:
d
dT
u ρ dv = M ar cvar E + (har TE − Rar TETE )[m& ar e + (m& ar v − m& ar s ) − m& ar TC ] 5.1-51
∫
1
424
3 dt
dt VC
a TE e ωE
& − ∑ mh
& =h
∑ mh
ar TE
S
m& ar TC − har (m& ar v − m& ar s ) − har e m& ar e
5.1-52
E
62
na qual:
−
har = entalpia média do ar úmido dentro da célula;
−
har e = entalpia média do ar úmido do ambiente externo, admitido na célula.
Substituindo 5.1-52 e 5.1-51 em 5.1-46, e juntando os termos de forma
conveniente, vem:
dT
− M ar CV ar E = (m& ar v − m& ar s )(harTE − har ) + m& ar e (harTE − har e ) −
1
424
3 dt
a TE e ωE
5.1-53
RarTE ⋅ TE (m& ar e − m& ar s + m& ar v − m& ar TC )
O valor do calor específico do ar úmido varia menos de 10% dentro das condições
de entrada e de saída do VC, de forma que a equação 5.1-53 pode ser escrita em função
de valores médios do calor específico do ar úmido, fazendo:
harTE
ωEω
}
− har = cpar (TE − T )
5.1-54
na qual:
−
ωE ω
}
cpar = é o calor especifico médio entre as condições ωE , TE e ω , T , do ar úmido.
harTE − har e
ω E ω0
}
= cpar (TE − T0 )
5.1-55
na qual:
−
ω E ω0
}
cpar = é o calor especifico médio entre as condições ωE , TE e ω0 , T0 , do ar
úmido.
Substituindo 5.1-54 e 5.1-55 em 5.1-53:
63
ωEω
ωE ω0
}
}
dTE
− M ar CV ar
= (m& ar v − m& ar s ) cpar (TE − T ) + m& ar e cpar (TE − T0 ) −
1
424
3 dt
aTE
(
RarTE m& ar e − m& ar s + m& ar v − m& ar TC
5.1-56
)
Fazendo:
 m& ar s
m& ar v − m& ar s = m& ar v 1 −
 m& ar v

com
 m& ar s
1 −
 m& ar v




 = f

5.1-57
m& ar v − m& ar s = f ⋅ m& ar v
Substituindo 5.1-57 em 5.1-56 e multiplicando ambos os membros por (-1), temse:
ωE ω
}
dTE
M ar CV ar
= Rar TE m& ar e − m& ar s + m& ar v − m& ar TC − f ⋅ m& arV cpar (TE − T ) −
1
424
3 dt
(
)
a TE e ωE
5.1-58
ωE ω0
}
m& ar E cpar (TE − T0 )
5.1.6. Umidade absoluta
ωE
na entrada do trocador de calor
Tomando um volume de controle que contenha a massa de ar na entrada do
trocador de calor, compreendendo a região onde o fluxo de ar externo admitido
encontra-se com os fluxos de ar interno recirculado, conforme mostra a figura 5.1-2., e
escrevendo o balanço de massa do vapor de água contido no VC, tem-se:
dM A E
dt
= ( m& Av − m& As ) + m& Ae − m& A TC
5.1-59
64
na qual:
−
M A E = massa de vapor de água contida no volume de controle (VC);
−
m& Av = vazão mássica do vapor de água contido no fluxo de ar úmido provocado
pelos ventiladores de circulação do ar da célula;
−
m& As = vazão mássica do vapor de água contido no ar úmido saindo da célula;
−
m& Ae = vazão mássica do vapor de água contido no ar úmido admitido na célula;
−
m& A TC = vazão mássica do vapor de água contido no fluxo de ar úmido através do
trocador de calor.
Substituindo
M A E = ωE M gE ( ωE é a umidade absoluta média e M gE é a massa de
ar seco no VC) em 5.1-59 e diferenciando o produto
M gE
ωE M gE , vem:
dM gE
dωE
+ ωE
= ( m& Av − m& As ) + m& Ae − m& A TC
dt
dt
5.1-60
A variação da massa de ar seco no VC é:
dM gE
dt
= ( m& gv − m& gs ) + m& ge − m& gTC
5.1-61
na qual:
−
m& gv = vazão mássica do ar seco contido no fluxo de ar úmido provocado pelos
ventiladores de circulação do ar da célula;
−
m& gs = vazão mássica do ar seco contido no ar úmido saindo da célula;
−
m& ge = vazão mássica do ar seco contido no ar úmido admitido na célula;
−
m& gTC = vazão mássica do ar seco contido no fluxo de ar úmido através do
trocador de calor.
65
m& Av = ω m& gv , m& As = ω m& gs , m& Ae = ω0 m& ge e
Substituindo 5.1-61 em 5.1-60 ; fazendo
m& A TC = ωE m& gTC , ( ω é a umidade absoluta do ar úmido dentro da célula, ω0 é a umidade
absoluta do ar ambiente admitido na célula e
ωE
é a umidade absoluta média do ar
úmido dentro do VC) e simplificando a expressão, chega-se a:
M gE
5.2.
dωE
= ( m& gv − m& gs ) (ω − ωE ) + m& ge (ω0 − ωE )
dt
5.1-62
PRESSÃO
Tomando um volume de controle em torno do ar úmido contido na célula
(excluindo o trocador de calor e a pasta), e escrevendo o balanço de massa do ar seco
contido no VC, tem-se:
dM g
dt
= m& ge − m& gs
5.2-1
na qual:
−
M g = massa de ar seco dentro da célula;
−
m& ge = vazão mássica de ar seco exterior admitido na célula;
−
m& gs = vazão mássica de ar seco saindo da célula.
P = Pg + PA
5.2-2
na qual:
−
P = pressão absoluta do ar úmido na célula;
−
Pg = pressão parcial do ar seco na célula;
−
PA = pressão parcial do vapor de água contido no ar úmido da célula.
66
Pg =
Mg
V
Rg T
5.2-3
na qual:
−
V = volume da célula;
−
Rg = constante de gás ideal do ar seco;
−
T = temperatura média do ar úmido na célula.
PA =
MA
RAT
V
5.2-4
na qual:
−
V = volume da célula;
−
RA = constante de gás ideal do vapor de água contido no ar úmido da célula;
−
T = temperatura média do ar úmido na célula.
ω=
MA
Mg
5.2-5
na qual:
−
ω
= umidade absoluta do ar úmido dentro da célula.
Substituindo 5.2-3 a 5.2-5 em 5.2-2, tem-se:
P=
Escrevendo a massa
T
M g ( Rg + ω RA )
V
5.2-6
M g , em função da pressão P , vem:
Mg =
P
V
⋅
T ( Rg + ω RA )
5.2-7
67
Derivando em função do tempo, obtém-se:
dM g
dt
T ( Rg + ω RA )
=
dP
dω 
 dT
V − PV 
( Rg + ω RA ) + TRA
dt
dt 
 dt
T ²( R g +ω RA )²
Substituindo 5.2-8 em 5.2-1 e notando
( Rg + ω RA ) = R ar , para simplificar, tem-se:
dP
dT
dω
RarT −
Rar P − PTRA
dt
dt = m& − m&
V ⋅ dt
ge
gs
T ² R ² ar
Isolando
5.2-8
5.2-9
dP dt e simplificando a expressão, chega-se a:
dP TRar
P dT RA P d ω
=
(m& ge − m& gs ) +
+
dt
V
T dt
Rar dt
5.2-10
5.2.1. Vazões de entrada e de saída de ar
As vazões de entrada e de saída de ar da célula são controladas por uma perda de
carga variável, no duto de admissão, provocada pela variação do ângulo de abertura do
damper.
Genericamente:
∆P = C
ρV ²
2
5.2-11
68
na qual:
−
∆P = perda de carga causada pela singularidade em questão;
−
C = coeficiente de perda de carga da singularidade;
−
ρ
−
V = velocidade do ar passando pela singularidade.
= densidade do ar passando pela singularidade;
Escrevendo 5.2-11, em função da vazão em volume:
∆P = C
ρ  v&ar 
2
 
2 S 
5.2-12
na qual:
−
v&ar = vazão em volume do ar;
−
S = área da seção transversal do duto.
Isolando
v&ar , vem:
v&ar = S
2∆P
ρC
5.2-13
Escrevendo em função da vazão mássica do ar,
m& ar = ρ v&ar = ρ S
2∆P
ρC
m& ar = ρ v&ar , tem-se:
5.2-14
Ou, de forma mais conveniente:
m& ar = S
2ρ
⋅ ∆P
C
5.2-15
69
Escrevendo em função da vazão de ar em base seca, tem-se:
m& ar = m& g + m& A = m& g (1 + ω )
5.2-16
na qual:
−
m& ar = vazão mássica do ar úmido;
−
m& g = vazão mássica de ar seco;
−
m& A = vazão mássica do vapor de água contido no ar úmido;
−
ω
= umidade absoluta do ar úmido.
Isolando
m& g , vem:
m& g =
1
m& ar
1+ ω
5.2-17
Substituindo 5.2-15 em 5.2-17, chega-se a:
m& g =
S
1+ ω
2 ρ ar
⋅ ∆P
C
5.2-18
Particularizando 5.2-18 para a vazão de ar admitido na célula, vem:
1
1
S  2 ρ0 ar  2
2
&
mge =

 ⋅ ( Patm − P)
1 + ω0  C (θ ) 
5.2-19
na qual:
−
ω0
−
ρ 0 ar
−
C (θ ) = coeficiente de perda de carga variável em função do ângulo de abertura
= umidade absoluta do ar ambiente externo ao secador;
= densidade do ar ambiente externo ao secador;
do damper;
−
Patm = pressão atmosférica do ambiente externo ao secador;
−
P = pressão interna do secador.
70
Particularizando 5.2-18 para a vazão de ar saindo na célula, vem:
1
1
S  2 ρ ar  2
&
mgs =
⋅ ( P − PVent ) 2
1 + ω  C 
5.2-20
na qual:
−
ω
−
ρ ar
−
C = coeficiente de perda de carga da transição do secador para o duto de saída;
−
Pvent = pressão na sucção do ventilador de exaustão;
−
P = pressão interna do secador.
= umidade absoluta do ar úmido interno ao secador;
= densidade do ar úmido interno ao secador;
A variação do coeficiente de perda de carga para o damper adotado para o projeto
básico do secador está na tabela 5.2-1.
m ar
Tabela 5.2-1 – Coeficiente de perda de carga para damper tipo borboleta
θ
D/D0
0
10
20
30
40
50
60
70
75
80
85
90
0,8 0,19 0,45 0,87 1,55 2,6 4,13 6,14 8,38 9,4
10,3
10,8
15
0,9 0,19 0,05 1,22 2,51 4,97 9,57 17,8 30,5 38
45
50,1
100
1
0,19 0,07 1,76 4,38 11,2 32 113 619 2010 10360 99999 99999
FONTE: ASHRAE Handbook, 1997
71
O coeficiente de perda de carga para o duto de exaustão foi extraído da tabela
5.2-2, com L/D = 0.
L
Tabela 5.2-2 – Coeficiente de perda de carga para duto instalado em parede.
L/D0
t/D0
0,000
0,002
0,01
0,05
0,01
0,5
0,57 0,68 0,08
0,5
0,51 0,52 0,55
0,02
FONTE: ASHRAE Handbook, 1997
5.3.
0,10
0,20
0,30
0,50
10,00
0,086
0,6
0,92
0,66
0,97
0,69
1
0,72
1
0,72
UMIDADE ABSOLUTA
Tomando um volume de controle em torno do ar úmido contido na célula
(excluindo o trocador de calor e a pasta), e escrevendo o balanço de massa do vapor de
água contido no VC, tem-se:
dM A
= m& AP + m& Ae − m& As
dt
(
)
5.3-1
na qual:
−
dM A
= variação de massa de vapor de água no VC;
dt
−
m& AP = massa de água trocada com o macarrão;
−
( m&
Ae
− m& As ) = diferença entre os fluxos de massa de vapor de água no ar úmido
entrando e saindo do VC.
72
Considerando que:
dM A d 
M 
= Mg A 
dt
dt 
M g 
5.3-2
MA
=ω
Mg
5.3-3
nas quais:
−
M g = massa de ar seco no VC;
−
M A = massa de vapor de água no ar úmido contido no VC;
−
ω
= umidade absoluta do ar úmido no VC.
Substituindo 5.3-3 em 5.3-2:
dM g
dM A d
dω
= (M g ⋅ ω ) = M g
+ω
dt
dt
dt
dt
5.3-4
Como:
dM g
dt
= (m& gee− m& gs )
5.3-5
na qual:
−
m& ge = vazão mássica de ar seco entrando no VC;
−
m& gs = vazão mássica de ar seco saindo do VC.
Substituindo 5.3-5 em 5.3-4, vem:
dM A
dω
= Mg
+ ω (m& gee− m& gs )
dt
dt
5.3-6
Substituindo 5.1-18, 5.1-19 e 5.3-6 em 5.3-1, tem-se:
73
Mg
dω
= −ω (m& ge − m& gs ) + m& AP + ω0 m& g e − ω m& gs
dt
5.3-7
na qual:
−
ω0
= umidade absoluta do ar ambiente externo ao secador.
Simplificando chega-se a :
Mg
5.4.
dω
= m& ge (ω0 − ω ) + m& AP
dt
5.3-8
TEMPERATURA DE SAÍDA DA ÁGUA QUENTE
Tomando um volume de controle em torno do trocador de calor e escrevendo o
balanço de energia:
d
& − ∑ mh
&
Q& liq =
∫ u ρ dv + ∑S mh
dt VC
E
Q& liq = 0
5.4-1
desprezando perdas de calor.
d
d
u ρ dv = (um M m + uar M ar + uaq M aq )
∫
dt VC
dt
5.4-2
74
na qual:
−
um = energia interna média do metal do trocador de calor;
−
M m = massa de metal do trocador de calor;
−
uar = energia interna média do ar úmido dentro do VC;
−
M ar = massa de ar úmido dentro do VC;
−
uaq = energia interna média da água quente dentro do trocador de calor;
−
M aq = massa de água quente dentro do trocador de calor.
A massa de ar úmido
M ar contida no volume de controle é muito pequena em
comparação às massas de metal e de água quente (para um trocador de calor com
volume igual a 2m x 0,5m x 0,2m, é de cerca de 0,15 kg), portanto sua capacidade
térmica pode ser desprezada.
& − ∑ mh
& =  m&
∑ mh
aq s
S
haq s + m& g s hg s + m& As hAs  −  m& aqe haqe + m& ge hge + m& Ae hAe 
5.4-3
E
na qual:
−
m& aqe , m& aq s = vazões em massa da água quente entrando e saindo do trocador de
calor (TC);
−
haqe , haq s = entalpias da água quente entrando e saindo do TC;
−
m& ge , m& g s = vazões em massa do ar seco entrando e saindo do TC;
−
hge , hg s = entalpias do ar seco entrando e saindo do TC;
−
m& Ae , m& As = vazões em massa do vapor de água entrando e saindo do TC;
−
hAe , hAs = entalpias do vapor de água entrando e saindo do TC.
Substituindo 5.4-3 e 5.4-2 em 5.4-1, tem-se:
75
Mm
d µaq
dum
+ M aq
+  m& aq s haq s + m& g s hg s + m& As hAs  −  m& aqe haqe + m& ge hge + m& Ae hAe  = 0
dt
dt
5.4-4
Considerando:
dum = cm dTm
5.4-5
na qual:
−
cm = calor específico do metal do trocador de calor (TC);
−
Tm = temperatura média do metal do trocador de calor;
duaq = caq dTaq
5.4-6
na qual:
−
caq = calor específico da água quente;
−
Taq = temperatura média da água quente.
O coeficiente de película do lado da água é muito maior que o do lado do ar, então
a temperatura média
temperatura média
Tm do trocador de calor pode ser admitida muito próxima da
Taq da água quente.
Tm ≈ Taq
5.4-7
A água é incompressível, então:
m& aqe = m& aq s
5.4-8
76
O ar a baixas velocidades pode ser considerado como incompressível e não há
variação de pressão significativa através do trocador de calor, a perda de carga é
desprezível. Também não há perda ou adição de vapor de água dentro do trocador de
calor no lado do ar, então tem-se:
m& ge = m& g s = m& g TC
m& Ae = m& As = m& A TC
5.4-9
5.4-10
Considerando também:
haqe − haq s = caq (Taq e − Taq s )
5.4-11
hg e − hg s = cpg (TE − TT )
5.4-12
hAe − hAs = cp A (TE − TT )
5.4-13
nas quais:
−
cpg = calor específico a pressão constante do ar seco;
−
cp A = calor específico a pressão constante do vapor de água contido no ar úmido;
−
TE = temperatura do ar úmido na entrada do trocador de calor;
−
TT = temperatura do ar úmido na saída do trocador de calor;
Substituindo 5.4-5 a 5.4-13 em 5.4-4 e re-arranjando os termos, chega-se a :
( M m cm + M aq caq )
dTaq
dt
= m& aq caq (Taqe − Taq s ) + m& g TC cp g (TE − TT ) + m& A TC cp A (TE − TT )
5.4-14
77
Escrevendo a vazão de vapor de água
e da umidade absoluta
m& A TC em função da vazão de ar seco m& g TC
ωE , do ar úmido que atravessa o trocador de calor, tem-se:
m& A TC = ωE m& g TC
5.4-15
Para evitar erro numérico nos cálculos relativos à dinâmica do sistema de
controle, é necessário usar a hipótese da “célula doante”, na qual a propriedade média
precisa ser admitida igual à propriedade na saída da célula, assim:
Taq = Taq S
5.4-16
Substituindo 5.4-16 e 5.4-15 em 5.4-14, tem-se:
( M m cm + M aq caq )
dTaq s
dt
= m& aq caq (Taqe − Taq s ) − m& g TC (cp g + ω E cp A )(TT − TE ) 5.4-17
Pode-se simplificar a notação usando
( M m cm + M aq caq )
dTaq s
dt
cp g + ωE cp A = cpar E , de forma a ficar:
= m& aq caq (Taqe − Taq s ) − m& g TC cpar TE (TT − TE )
5.4-18
5.4.1. Cálculo da temperatura do ar úmido na saída do trocador de calor
Cálculo da temperatura do ar úmido de saída do trocador de calor pelo método
“ ε -NUT” (INCROPERA e DE WITT, 2002).
Definindo:
Ch = m& aq ⋅ c aq
5.4-19
78
Cc = m& gTC cp arTE
5.4-20
nas quais:
−
Ch = capacidade calorífica da corrente quente;
−
Cc = capacidade calorífica da corrente fria;
−
m& aq = vazão de água quente;
−
c aq = calor específico da água quente;
−
m& gTC = vazão do ar úmido;
−
cp arTE = calor específico do ar úmido.
Cmax = max(Ch , Cc )
5.4-21
Cmin = min(Ch , Cc )
5.4-22
CR =
Cmin
Cmax
NUT =
UA
Cmin
5.4-23
5.4-24
na qual:
−
U = coeficiente global de troca do trocador de calor;
−
A = área de troca do trocador de calor.
qmax = Cmin (Th ,i − Tc,i ) = Cmin (Taq E − TE )
5.4-25
q = Ch (Th ,i − Th ,o ) = C c (Tc ,o − Tc,i ) = m& gTe ⋅ cparTE (TT − TE )
5.4-26
79
nas quais:
−
Th ,i = temperatura de entrada do fluido quente;
−
Th,o = temperatura de saída do fluido quente;
−
Tc ,i = temperatura de entrada do fluido frio;
−
Tc ,o = temperatura de saída do fluido frio.
ε=
q
5.4-27
qmax
na qual:
−
ε
= efetividade
Para escoamento cruzado (como no trocador de calor tipo compacto escolhido),
com um só passe em cada corrente e fluidos não misturados, tem-se:
 1 

0,22
exp  −CR ( NUT )0,78  − 1 
 ( NUT )
 C R 

{
ε = 1 − exp 
}
5.4-28
De 5.4-25, 5.4-26 e 5.4-27, tem-se:
m& gTC cp arTE (TT − TE ) = ε ⋅ Cmin (Taqe − TE )
Isolando
5.4-29
TT , obtém-se:
TT = TE +
ε ⋅ Cmin (Taq E − TE )
m& gTC ⋅ cparTE
5.4-30
80
5.5.
UMIDADE DA PASTA
Conforme exposto em 3.1 adotou-se o modelo proposto por KÜÇÜK e ÖZILGEN
(1997) para a adequação do estudo da secagem de macarrão feito em batelada e escala
de laboratório para secagem contínua em secador industrial.
A umidade de equilíbrio é calculada pela expressão da equação 2.3-1:
 ϕ 
X e = (1 + ξ ) (0,154 − 1, 22 ×10−3 × T ) 

 1−ϕ 
( 0,078+ 7,32×10
−3
×T
)
na qual:
−
X e = umidade de equilíbrio;
−
ϕ
−
T = temperatura média do ar úmido dentro da célula;
−
ξ
= umidade relativa do ar úmido dentro da célula;
= fator de correção para uso da equação em processos contínuos.
A umidade média do macarrão no final de cada célula é calculada pela equação
2.3-3, proposta por ANDRIEU e STAMATOPOULOS (1986):
 β12 Dt 
X − Xe
4
=
exp  − 2 
 Rp 
X 0 − X e β12


Isolando
X , tem-se:
 β12 Dt 
X = X e + ( X 0 − X e ) 2 exp  − 2 
 Rp 
β1


4
5.5-1
No secador contínuo, o tempo que a pasta fica exposta ao meio ambiente de
secagem é função da velocidade da esteira que carrega as varas com as tiras de
espaguete e o comprimento da célula.
81
t=
L
vP
5.5-2
Substituindo 5.5-2 em 5.5-1, chega-se a:
X = Xe + ( X0 − Xe )
 β12 D L 
exp
 − 2

β12
 R p vP 
4
5.5-3
Na qual:
−
X = umidade média do macarrão ao final do percurso na célula;
−
X 0 = umidade média do macarrão no início do percurso na célula;
−
β1
−
D = difusividade efetiva da água na pasta;
−
RP = raio do cilindro de espaguete;
−
L = comprimento da célula;
−
vP = velocidade de translação da esteira carregando as varas com pasta.
= primeiro termo da função de Bessel de primeira espécie e ordem zero;
82
6. PROJETO BÁSICO DO SECADOR
Para a modelagem definiu-se um secador para pasta longa baseado em (i)
processo de secagem recomendado por MILATOVICH e MONDELLI (1990), (ii) secadores
descritos por MILATOVICH e MONDELLI (1990) e (iii) secador industrial observado em
visita a pastifício.
6.1.
PROCESSO DE SECAGEM
Optou-se por processo de secagem de espaguete a altíssima temperatura, como é
a tendência atual, seguindo as recomendações de MILATOVICH e MONDELLI (1990). O
processo de secagem definido compreende três fases na pré-secagem e seis fases na
secagem final. Cada fase é processada em uma câmara ou célula.
O tempo percorrido e a umidade da pasta atingida ao final de cada fase são
mostrados no gráfico 6.1-1.
Curva de Secagem
Umidade da pasta (kg agua/kg pasta seca)
45
40
35
30
25
20
15
10
5
0
0
1
2
3
4
5
6
Tempo de percurso (horas)
Gráfico 6.1-1 - Curva de secagem conforme recomendações de
MILATOVICH e MONDELLI (1990)
83
Os parâmetros de operação estão resumidos na tabela 6.1-1.
Tabela 6.1-1 - Parâmetros de operação do secador
Fase do
processo
Tempo
de
percurso
da pasta
Umidade
da pasta
Umidade
de
equilibrio
Temperatura
da célula
Difusividade
efetiva
Umidade
relativa do
ar da celula
Umidade
absoluta do
ar da célula
Água
evaporada da
pasta
Ar ambiente
admitido na
célula 35ºC
95%
Ar ambiente
admitido na
célula 20ºC
20%
t
X
Xe
T
D
ϕ
ω
mAP
mge
mge
x10-11
(%)
(kg de
vapor/kg
de ar seco)
(kg/s)
(kg/s)
(kg/s)
2
(horas)
Inicial
Présecagem
Secagem
Célula
1
Célula
2
Célula
3
Célula
1
Célula
2
Célula
3
Célula
4
Célula
5
Célula
6
6.2.
(%)
(%)
(ºC)
(m /s)
0,00
40,8
0,33
32
20,58
50
2,11
79,87
0,075
0,04323
1,064
0,592
0,67
26,5
20,22
70
2,72
82,09
0,242
0,02702
0,13
0,111
1
22,5
18,73
98
3,69
86,99
3,833
0,01965
0,0052
0,0049
1,75
16,7
13,82
90
3,4
78,58
0,945
0,02849
0,0313
0,0294
2,5
14,4
13,25
90
3,4
77,62
0,916
0,0113
0,0128
0,012
3,25
14,1
13,73
85
1,061
76,39
0,581
0,00147
0,0027
0,0025
4
13,8
13,43
85
1,06
75,81
0,573
0,00147
0,0027
0,0025
4,75
13,5
13,09
70
0,086
68,7
0,19
0,00147
0,0095
0,0078
5,5
13,1
12,56
70
0,086
67,16
0,184
0,00196
0,0131
0,0107
CÁLCULO DOS PARÂMETROS DE OPERAÇÃO DO SECADOR
6.2.1. Umidade de equilíbrio
Usou-se os valores das colunas “Tempo de percurso da pasta” e “Umidade da
pasta”, da tabela 6.1-1, extraídos, por sua vez, da curva de secagem da figura 6.1-1,
juntamente com os valores da coluna “Difusividade efetiva” (recomendados por KÜÇÜK e
ÖZILGEN (1997)), inseridos na equação 2.3-3, para cálculo do parâmetro
X e umidade
de equilíbrio, cujo valor deverá ser garantido pelas condições de temperatura e umidade
relativa na célula.
Os valores de
X e calculados estão tabulados na respectiva coluna da tabela 6.1-1
6.2.2. Umidade relativa
Conforme exposto no capítulo 3 optou-se pelo modelo de isoterma proposto por
KÜÇÜK e ÖZILGEN (1997), equação 2.3-1, para definição do processo de secagem.
84
Inseriu-se os valores de temperatura de cada fase conforme recomendações de
MILATOVICH e MONDELLI (1990), tabulados na coluna “Temperatura da célula”, da
tabela 6.1-1, e os correspondentes valores de
X e , umidade de equilíbrio, calculados em
6.2.1, na equação 2.3-1, para cálculo dos valores de umidade relativa
ϕ.O
valor obtido,
operando em cada célula, juntamente com o valor correspondente de temperatura
T,
garantirá o valor da umidade de equilíbrio, necessário para atingir o valor da umidade da
pasta
X programado para cada fase do processo.
Os valores de
ϕ
calculados estão tabulados na coluna “Umidade relativa do ar da
célula” da tabela 6.1-1.
6.2.3. Umidade absoluta
Calculou-se a umidade absoluta
ω,
parâmetro importante no estudo do balanço
de massa, para a modelagem da célula, pela equação 2.1-6, usando-se a umidade
relativa
ϕ,
calculada em 6.2.2 e a pressão de vapor
pv , à temperatura T do ar da
célula, calculada pela equação de Antoine:
pv = 133, 3224 × 10
B

2
 A+ T + C log T + DT + ET 


6.2-1
A = 16,373
B = −2818, 6 C = −1, 6908
D = −5, 7546 ×10
−3
pv em Pa e T em K.
Os valores de
ω
calculados estão tabulados na coluna “Umidade absoluta do ar da
célula” da tabela 6.1-1.
6.2.4. Perda de umidade da pasta
Calculou-se a perda de umidade da pasta
m& AP , em cada fase do processo, como o
X 0 e a umidade final X , que é a umidade
& P , conforme equação
atingida pela pasta na saída da célula, pelo fluxo de macarrão m
produto da diferença entre a umidade inicial
6.2-3.
85
Na primeira célula da pré-secagem, a umidade inicial
X 0 é a umidade da massa
extrudada que é alimentada no secador. Nas demais células,
X 0 é a umidade do
macarrão na saída da célula imediatamente anterior.
Tomando-se o balanço de massa para um volume de controle envolvendo o
macarrão dentro da célula, tem-se para a água:
m& P X 0 = m& AP + m& P X
6.2-2
m& AP = m& P ( X 0 − X )
6.2-3
m& P é o fluxo de macarrão, em base seca, que passa pelo secador.
A produção
m& Pu , em base úmida, adotada como nominal do secador é de
2000 kg/hora, a produção
m& P , em base seca, é:
m& P =
m& Pu
1
(1 + X ) 3600
6.2-4
Para uma umidade final de 13,1% (0,131 kg de água/kg de pasta seca), o fluxo
de macarrão
m& P é de 0,49 kg/s.
Os valores de
m& AP calculados estão tabulados na coluna “Água evaporada da
pasta” da tabela 6.1-1.
6.2.5. Vazão de ar ambiente admitido
Como visto em 6.2.2 a umidade do ar interno à célula determina a umidade de
equilíbrio e em consequência a umidade da pasta. A manutenção da umidade do ar
interno
ω , é feita com a admissão de ar ambiente (externo ao secador) e exaustão de ar
interno. Esta troca de ar compensa a umidade cedida pela pasta com o menor teor de
umidade
ω0
contido no ar ambiente admitido.
Calculou-se a vazão de ar seco
m& ge , necessária para a manutenção da umidade do
ar interno, em valor adequado, tomando um volume de controle coincidindo com a
parede interna da célula, porém excluindo a pasta, de forma que o volume de controle
contém todo o ar interno à célula.
86
Em regime, os balanços de massa para o vapor de água e para o ar seco
resultam:
Para o vapor de água:
m& geω0 + m& AP = m& gsω
6.2-5
m& ge = m& gs
6.2-6
e para o ar seco:
Substituindo 4-5 em 4-4, resulta:
m& ge =
m& AP
ω − ω0
6.2-7
A condição ambiente de referência para o projeto básico do secador é a condição
de verão, que é mais severa do ponto de vista da umidade relativa ambiente. A condição
adotada, neste trabalho, para o verão é temperatura do ar de 35ºC e umidade relativa
de 95%.
A tabela 6.1-1 apresenta o desempenho do secador na situação de ar ambiente de
verão, no entanto está tabulada também a vazão de ar externo na situação de ambiente
de inverno, 20ºC e umidade relativa de 20%, pois foi necessária para o cálculo da
capacidade do trocador de calor.
Os valores de
m& ge calculados estão tabulados nas colunas “Ar ambiente admitido
na célula” da tabela 6.1-1.
6.3.
ESTUDO DO TROCADOR DE CALOR
Para o projeto básico do trocador de calor é necessário conhecer as temperaturas
de entrada e de saída da água quente e do ar úmido e a vazão mássica do ar úmido em
regime.
As temperaturas de entrada e saída da água quente são condições de projeto e
dependem do equipamento gerador de água quente escolhido. Adotou-se temperatura de
entrada de água quente
Taqe = 130ºC e temperatura de saída Taqs = 110ºC.
87
A temperatura de entrada do ar úmido no trocador de calor calcula-se pela
equação 5.1-58 escrita para a condição de regime,
dTE dt = 0 :
ω E ω0
ωEω
}
}
f ⋅ mg v (1 + ω ) cpar T + mg e (1 + ω0 ) cpar T0
TE =
ωE ω
ωE ω0
}
}
f ⋅ mgv (1 + ω ) cpar + mge (1 + ω0 ) cpar
6.3-1
A umidade absoluta na entrada do trocador de calor calcula-se pela equação 5.162 escrita para a condição de regime,
ωE =
Lembrando que
d ωE dt = 0 :
ω mgv − ω mgs + ω0 mge
6.3-2
mgv − mgs + mge
cpar = cpg + ω cp A , calor especifico do ar úmido, base seca, pode
ser calculado a partir dos calores específicos do ar seco (1005 J/kg.K) e do vapor de água
(1900 J/kg.K), para as diversas condições conforme tabela 6.3-1.
Tabela 6.3-1 – Valor do calor especifico do ar úmido para diversas condições
Temperatura
do ar úmido
Umidade
relativa do ar
úmido
Umidade
absoluta do ar
úmido
Calor específico do
ar úmido
T
ϕ
ω
cpar
(ºC)
(%)
(kg de vapor/kg
de ar seco)
(J/kgK)
20
35
46
71
50
20
95
79,87
0,00286
0,03435
0,065
0,065
0,075
1010,434
1070,265
1128,5
1128,5
1147,5
A vazão de ar úmido através do trocador de calor é função das vazões de ar
admitido e ar de exaustão e vazão de ar dos ventiladores (axiais) de circulação.
Escolheu-se a vazão dos ventiladores a partir da velocidade recomendada do ar
(10 m/s) e área da seção dos ventiladores. Os dois ventiladores axiais de 0,60 m de
diâmetro tem a área total de 0,566 m2, então a vazão total dos dois é de:
88
10
m
kg
kg
× 5, 66m 2 × 0,8 3 = 4, 5
s
m
s
6.3-3
E a vazão de ar seco é:
m& gv =
m& ar v
(1 + ω )
=
4,5
(1 + 0, 075 )
4, 2
kg
s
6.3-4
Com as equações 6.3-1 a 6.3-4 e os valores da tabela 6.3-1 calculou-se os
valores das temperaturas de entrada
6.3-2 mostra os valores de
TE , e de saída TT , no trocador de calor. A tabela
TE , TT e ωE , para as situações de verão e de inverno.
Tabela 6.3-2 – Temperaturas de entrada e de saída do trocador de calor
Temperatura
ambiente
Umidade
relativa
ambiente
Umidade
absoluta na
entrada do
trocador
Temperatura
na entrada
do trocador
Temperatura
na saída do
trocador
T0
ϕ0
ωΕ
TΕ
TT
(ºC)
(%)
(ºC)
(ºC)
Inverno
20
20
0,066
46,02
71,74
Verão
35
95
0,065
46,3
71,77
A vazão de água quente no trocador de calor calcula-se pela equação 5.4-18
escrita para a condição de regime,
dTaqs dt = 0 :
m& aq caq (Taqe − Taq s ) − m& g TC cpar E (TT − TE )
6.3-5
89
Os valores calculados estão na tabela 6.3-3.
Tabela 6.3-3 – Vazão de água quente
Temperatura
ambiente
Umidade
relativa
ambiente
ϕ0
Vazão de água
quente no
trocador de
calor
T0
(ºC)
(%)
maq
(kg/s)
Inverno
20
20
1,457
Verão
35
95
1,441
Com esses valores calcula-se a capacidade de troca térmica
global de troca térmica x área do trocador de calor), pelo método
UA (coeficiente
ε , NUT ,
com as
equações 5.4-19 a 5.4-28, conforme detalhado no anexo 1. Os valores calculados estão
tabulados na tabela 6.3-4.
Tabela 6.3-4 – Valores de capacidade de troca térmica ( UA )
Ar ambiente
Capacidade de
troca térmica
Temperatura
Umidade
relativa
T0
(ºC)
(%)
UA
(W/K)
Inverno
20
20
1468
Verão
35
95
1761
Com os valores de
ϕ0
UA , e o comprimento dos tubos do trocador, escolhido pela
geometria da célula como sendo de 2m, calculam-se o coeficiente global de troca térmica
U e a área A do trocador de calor, conforme detalhado no anexo 2. Os valores de A , e
a correspondente quantidade de tubos aletados estão na tabela 6.3-5.
90
Tabela 6.3-5 – Área necessária para cada situação ambiente extrema
Ar ambiente
Temperatura
Umidade
relativa
T0
ϕ0
Coeficiente
global de
troca
térmica
Quantidade
de tubos
aletados
U
Área de
troca do
lado do ar
A
2
(m2)
(ºC)
(%)
(W/m K)
Inverno
20
20
89,4
10
16,4
Verão
35
95
86
12
20,5
Como previsto a condição mais severa de trabalho é no verão devido à elevada
umidade relativa, a escolha necessária para a construção do trocador é com 12 tubos e
20,5 m2 de área de troca do lado do ar.
Observa-se que o coeficiente global de troca térmica varia conforme variam as
vazões de água quente e de ar, para introduzir essa variação no modelo construído no
software Simulink (MATLAB) usado para a simulação, calculou-se o coeficiente global de
troca térmica, para o trocador com 20,5m2, para intervalos de vazões de ar e de água
quente que contenham a operação do secador dentro dos limites ambientes estudados.
Os valores de
U estão na tabela 6.3-6 e gráfico 6.3-1.
Tabela 6.3-6 – Variação do coeficiente global de troca térmica
m& aq
m& g TE
(kg/s)
(kg/s)
3,8
4
4,2
0,5
64,3
65,4
66,3
1
74,8
76,3
77,6
1,5
79,6
81,3
82,8
2
82,5
84,3
85,9
91
Variação de U com mg TE e m aq
90
85
mgmTEg(kg/s)
TE(kg/s)
2
U (W/m
K)
U
80
3,8
4
75
4,2
70
65
60
0
0,5
1
1,5
2
2,5
m aq
maq(kg/s)
Gráfico 6.3-1 - Variação do coeficiente global de troca térmica
92
7. SIMULAÇÃO E RESULTADOS
Para a simulação do modelo dinâmico construído foi usado o “toolbox” Simulink do
MATLAB.
Usando as definições do secador, em termos de dimensões e quantidades,
fornecidas no capitulo 6, “Projeto básico do Secador”, construiu-se as equações
deduzidas no capitulo 5, “Modelagem” no software Simulink. As principais equações estão
mostradas no anexo 3.
Para mostrar o desempenho da modelagem simulou-se a operação do secador
iniciando com um ambiente externo de inverno (20ºC e 20% de umidade relativa) com
as variáveis de controle (vazão de água quente e ângulo do damper) ajustadas para
levar as variáveis de estado: propriedades do ar úmido da célula (temperatura, pressão e
umidade relativa), da água quente (temperatura de saída do trocador de calor), e da
pasta (umidade de equilíbrio e umidade média ao final do percurso na célula) aos valores
de operação em regime. O ponto de partida para este ajuste foram os valores para vazão
de água quente e vazão de ar admitido calculados no capítulo “Projeto básico do
Secador”.
A simulação prosseguiu nessas condições por 5 min, tempo suficiente para o
processo entrar em regime.
A seguir simulou-se uma mudança no ambiente no qual o secador opera, mudouse para o ambiente de verão (35ºC e 95% de umidade relativa), sem alterar as variáveis
de controle. O objetivo desse procedimento é observar a variação ocorrida nas
propriedades do ar úmido e da pasta quando mudam as condições externas e o sistema
de controle não atua.
A simulação prosseguiu por mais 5min, tempo suficiente para o processo entrar
novamente em regime.
Simulou-se, então, a atuação do sistema de controle, ajustando a abertura do
damper e a vazão de água quente, usando como base os valores calculados em “Projeto
básico do secador”.
A simulação prosseguiu por outros 5min, até o processo entrar novamente em
regime.
93
Constatou-se que ao atingir novamente a condição de operação em regime as
propriedades do ar úmido e da pasta voltaram aos valores desejados, indicados na tabela
6.1-1, já comentada.
Os gráficos 7.1-1 a 7.1-4 ilustram a simulação descrita.
Além de obter-se gráficos para ilustrar a simulação, foi montado um painel de
controle no Simulink, mostrado no anexo 4, com indicadores numéricos, para uma leitura
mais precisa.
Observou-se que, à exceção da vazão de água quente e, em consequência, a
temperatura de saída da água quente, todos as variáveis atingiram exatamente os
valores previstos no “Projeto básico do secador”.
A razão da diferença de cerca de 5% para o valor da vazão de água quente devese ao fato de que, no cálculo daquele valor feito no “Projeto básico do secador”, por se
tratar de um valor de referência, foi adotado para o calor específico do ar úmido que
atravessa o trocador de calor, um valor médio aproximado. No modelo construído no
Simulink, o calor específico do ar úmido é calculado em tempo real a partir dos calores
específicos do ar seco e vapor de água e da umidade absoluta do ar úmido na entrada do
trocador de calor, também calculada em tempo real.
94
7.1.
SIMULAÇÃO
A seguir estão os gráficos com as variações das variáveis mais importantes.
TEMPERATURAS
80
Te
T
TT
75
T ( ºC )
70
65
60
55
50
45
0
100
200
300
400
500
600
700
Operando com variaçao de 20ºC 20% a 35ºC 95%
800
900
Gráfico 7.1-1 – Variação das temperaturas do ar úmido
UMIDADE RELATIVA NA CELULA
0.82
UR ( % )
0.815
0.81
0.805
0.8
0.795
0
100
200
300
400
500
600
700
Operando com variaçao de 20ºC 20% a 35ºC 95%
800
900
Gráfico 7.1-2 – Variação da umidade relativa
95
UMIDADE DE EQUILIBRIO NA CELULA
Xe ( kg de agua / kg de pasta seca )
0.22
0.215
0.21
0.205
0.2
0.195
0
100
200
300
400
500
600
700
Operando com variaçao de 20ºC 20% a 35ºC 95%
800
900
Gráfico 7.1-3 - Variação da umidade de equilíbrio
UMIDADE MEDIA DA PASTA NA SAIDA DA CELULA
X ( kg de agua / kg de pasta seca )
0.33
0.325
0.32
0
100
200
300
400
500
600
700
Operando com variaçao de 20ºC 20% a 35ºC 95%
800
900
Gráfico 7.1-4 – Variação da umidade média da pasta ao sair da célula
96
A análise da célula para construção do modelo dinâmico indicou duas regiões
características: (i) mistura de correntes de ar úmido antes do trocador de calor e (ii) ar
úmido da célula como um todo. As duas regiões foram modeladas usando o mesmo
método, ou seja foram estudadas como suas variáveis se alteram com o tempo.
Observou-se a dinâmica da região antes do trocador de calor é muito mais rápida
que a dinâmica do resto da célula, de forma que o transiente daquela região não tem
influência significativa na dinâmica da célula, podendo ser estudada em regime
permanente sem prejuízo dos resultados gerais da célula.
Para comprovar esta última afirmação foram construídos dois modelos, um
primeiro modelo com todas as variáveis calculadas por integração da expressão de sua
variação com o tempo em função da própria variável e das demais, e um segundo
modelo, no qual as variáveis temperatura e umidade absoluta do ar úmido antes do
trocador de calor foram calculadas algebricamente, por equações resultantes da
aplicação do balanço de massa e de energia para situação de regime permanente.
O resultado da simulação dos dois modelos em situações idênticas mostrou que
não há diferença significativa nos valores das variáveis em qualquer instante do tempo,
como mostra o gráfico 7.1-5.
COMPARAÇAO TE INTEGRADO E ALGEBRICO
54
Te-int
Te-alg
53
52
Te ( ºC )
51
50
49
48
47
46
45
0
100
200
300
400
500
600
700
Operando com variaçao de 20ºC 20% a 35ºC 95%
800
900
Gráfico 7.1-5 – Comparação TE algébrico x TE integrado
97
8. CONCLUSÕES
Os resultados da simulação mostram que o modelo dinâmico desenvolvido neste
trabalho representa adequadamente o processo de secagem contínuo, uma vez que
alterando apenas as variáveis de controle disponíveis em um secador real (abertura do
“damper” e vazão de água quente) o modelo reconduz o processo à condição de regime
desejada, quando um desvio desta é provocado por uma perturbação no ambiente
externo ao equipamento.
O objetivo proposto, de modelar o processo de secagem de macarrão em secador
contínuo, de maneira a obter um modelo na forma adequada para ser linearizado e usado
para o projeto do sistema de controle, foi atingido, uma vez que o modelo dinâmico
desenvolvido apresenta a variação no tempo de cada variável de estado em função dela
mesma e das demais.
Na pesquisa bibliográfica feita não foi achado modelo dinâmico para secagem de
macarrão em processo contínuo, sendo este um modelo original de múltiplas aplicações.
O equacionamento obtido permite uma análise dinâmica do processo, que por sua vez
leva à avaliação do desempenho do equipamento permitindo uma otimização do projeto.
A análise do ambiente interno do secador, temperaturas, vazões de ar úmido,
umidades relativas e absolutas das diversas regiões auxiliam a compreender melhor o
processo de forma a dar subsídios para melhorar a operação do equipamento e a
qualidade do produto final.
O modelo dinâmico presta-se ao projeto de sistemas de controle para o
equipamento, e este modelo, da forma como foi construído, permite a montagem de
modelos de controle multivariável, pelos métodos do espaço dos estados, que
apresentam consideráveis vantagens com relação aos sistemas de controle clássicos,
quando tem-se que controlar um conjunto de variáveis fortemente interligadas, como é o
caso do equipamento de secagem de pasta, com sua várias células em sequência.
Entre os diversos tipos de sistemas de controle que podem ser desenvolvidos
pelos métodos do espaço dos estados está o “Controle Ótimo”, que permite fazer o
controle de todas as variáveis, em conjunto, obedecendo uma função de otimização, que
pode ser construída com diversos critérios, como minimizar o consumo de energia ou
otimizar parâmetros de qualidade do produto.
98
8.1.
CONCLUSÕES SOBRE A ESCOLHA DO MODELO
A proximidade dos resultados obtidos aplicando-se o modelo escolhido, com os
dados fornecidos por um fabricante de secadores industriais para pasta, publicados em
seu catálogo, sugerem que o modelo escolhido funciona para o processo de secagem
contínuo.
A escolha do modelo usado para descrever o processo de secagem do macarrão
deveu-se ao fato de ter-se originado de um estudo de adaptação de modelos
desenvolvidos em laboratório, com a secagem de pequenas quantidades, em ambiente
sob condições controladas e constantes, para uso na previsão da umidade da pasta
durante um processo de secagem em secador contínuo industrial.
Em etapa anterior do estudo havia-se optado por um modelo de secador no qual a
mistura do ar da célula com o ar admitido se dava após o trocador de calor, como mostra
a figura 8.1-1.
m ar s
Pvent
T
m ar e
T0
Patm
T
E
TT
m ar v
T
Figura 8.1-1– Modelo de secador com mistura após o trocador de calor
99
A simulação do modelo construído para esse tipo de secador mostrou um
funcionamento muito dependente das condições do ambiente externo, chegando a exigir
equipamento de troca de calor de dimensões descomunais para situações de baixa
umidade relativa ambiente.
Com baixa umidade relativa ambiente a vazão de ar externo necessário para
manter a umidade relativa interna, compensando a umidade cedida pela pasta, é muito
pequena, exigindo então uma temperatura após o trocador de calor muito elevada (da
ordem de 170ºC) para transportar a energia necessária para evaporar a água da pasta.
Essa inadequação levou à opção pelo tipo de secador (figura 4.1-1) estudado
neste trabalho.
A simulação do atual modelo, discutida no capitulo 7, mostrou uma robustez deste
tipo de secador com relação à variações das condições do ambiente externo, uma vez
que a energia necessária para o evaporação da água retirada da pasta é transportada por
uma vazão significativamente maior que a vazão do ar externo admitido, pois a maior
parte da vazão dos ventiladores é direcionada para a alimentação do trocador de calor.
8.2.
SUGESTÕES PARA TRABALHOS FUTUROS
O modelo dinâmico desenvolvido está pronto para ser linearizado e usado para o
projeto de controladores para o secador. A sugestão é projetar um controlador
multivariável usando as vantagens do método de “Controle Ótimo” para gerenciar e
otimizar aspectos importantes da operação do equipamento, como o uso de energia.
Outra possibilidade de prosseguimento deste trabalho é buscar uma correlação
mais estreita com o funcionamento de um secador industrial por meio da verificação de
dados levantados experimentalmente.
100
REFERÊNCIAS
(1) American
Society
of
Heating,
Refrigerating
and
Air-Conditioning
Engineers.
Fundamentals. ASHRAE Handbook. Atlanta. ASHRAE, 1997.
(2) ANDRIEU, J.; STAMATOPOULOS, A. Durum wheat pasta drying kinetics. Lebbensmittel
Wissenschaft und Technologie, 19 (1986), 448-456.
(3) ANDRIEU,
J.;
STAMATOPOULOS,
A.;
ZAFIROPOULOS,
M.
Equation
for
fitting
desorption isotherms of durum wheat pasta. Journal of Food Technology. 20 (1985),
651-657.
(4) CHOKMANI, K.;VIAU, A.; BOURGEOIS, G. Analyse de l’incertitude de quatre modeles
de phytoprotection relative á l’erreur de mesures de variables agro méteorologiques
d’entrée. Agronomie 21, 147-167.
(5) FRIEDLAND, B. Control System design. An Introduction to State-Space
Methods. Mineola. Dover Publications, 2005.
(6) INCROPERA, F. P.; DE WITT, D. P. Fundamentos de transferência de Calor e de
Massa. Rio de Janeiro. LTC, 2002.
(7) KÜÇÜK, R.; ÖZILGEN, M. Predicting dying behavior of spaghetti in a continuous
industrial dryer with the models determined in a lab scale batch system. Journal of Food
Processing and Preservation. 21 (1997), 245-256.
(8) KUDRA, T.; STRUMILLO C. Thermal Processing of Bio-materials. Quebec. CRC
Press, 1998.
(9) MILATOVICH, L.; MONDELLI, G. La Tecnologia della Pasta Alimentare. Pinerolo.
Chiriotti Editori, 1990, 330p.
(10)
ORMENESE, R. S. C.; LEITÃO, R.F.F.; SILVEIRA, N.F.A.; BALDINI, V.S. Influência
da secagem à alta temperatura nas características das massas com ovos. Ciência e
Tecnologia de Alimentos, vol. 18, no1, Campinas, 1998.
(11)
PAVAN S.p.A. Long-cut pasta line – catalogo.2007.
(12)
VAN WYLEN, G. J.; SONNTAG, R.E. Fundamentos da Termodinâmica Clássica.
São Paulo. Edgard Blücher, 1993.
(13)
VILLENEUVE, S.; GÉLINAS, P. Drying kinetics of whole durum wheat pasta
according to temperature and relative humidity. LWT. 40 (2006), 465-471.
(14)
WAANANEM, K. M.; OKOS, M. R. Effect of Porosity on Moisture Diffusion during
Drying of Pasta. Journal of Food Engineering. 28 (1996), 121-137.
101
ANEXO 1 – Cálculo da capacidade térmica
Cálculo de UA para a situação ambiente de 35ºC e 95% de umidade relativa
T0 = 35K
Te = 46.298K
TT = 71.776K
Taq e := 130K
Taq s := 110K
kg
mgv = 4.2
s
kg
maq := 0.1
s
Given
(
)(
mgv ⋅ cp we_ar ⋅ TT − Te
(
maq := Find maq
)
(
maq ⋅ cp aq ⋅ Taq e − Taq s
)
kg
maq = 1.441
s
)
Ch := maq ⋅ cp aq
J
Ch = 6023.992
s⋅K
Cc := mgv ⋅ cp we_ar
J
Cc = 4728.855
s ⋅K
(
)
J
Cmax = 6023.992
s⋅K
(
)
J
Cmin = 4728.855
s⋅K
Cmax := max Ch , Cc
Cmin := min Ch , Cc
Cmin
CR :=
Cmax
CR = 0.785
(
)
q max := Cmin⋅ Taq e − T0
(
)(
q := mgv ⋅ cp we_ar ⋅ TT − Te
ε :=
q max = 449241.267W
)
q
q max
q = 120479.84W
ε = 0.268
NUT := 1
Given
ε
0.78   
  1 

0.22  − C R ⋅NUT
 −1 
⋅
NUT
⋅
e


  CR 




1−e
NUT := Find ( NUT)
NUT = 0.372
UA := Cmin⋅ NUT
UA = 1760.9
W
K
Nota: Usou-se o software Mathcad para o cálculo, as abreviaturas sofreram modificação devido à limitação do
software.
102
ANEXO 2 – Cálculo do coeficiente global de troca térmica
"Dimensionamento TC com tubo de 22mm.mcd"
Cálculo do coeficiente global de troca térmica Uc e área Ac (quantidade de tubos) para a condição
extrema de funcionamento:
T0
UR
ºC
35
%
95
0
w
0
kg/kg
0.03435
kg/s
4.2
m
ºC/ºC
130/110
kg/s
1,4323
W/K
1748
Dados de projeto:
-(T0, UR0, Taqe)=fixados como condições de projeto
-mgv =vazão de ar seco através do TC em regime
-(UA, maq )=calculados para garantir a temperatura TT com Taqe/Taqs = 130/110, arquivo: "Analise TC_NUT_Te.mcd"
UA := 1761
W
K
kg
mgv := 4.2
s
kg
maq := 1.441
s
Cálculo do U
Propriedades:
Condutividade térmica do alumínio a 120ºC
W
kal := 238⋅
m⋅ K
Umidade absoluta do ar
wE := 0.066
Calor específico do ar seco (46ºC)
cp g := 1007
Calor específico do vapor (46ºC)
cp A := 1882
Calor específico do ar úmido
cp 0 := cp g + wE⋅ cp A
Calor específico da água quente (130ºC)
cp aq := 4278
Condutividade térmica da água quente
J
kg⋅ K
J
kg⋅ K
cp 0 = 1131.2
J
kg⋅ K
J
kg⋅ K
W
(130ºC) kaq := 0.688 m⋅ K
− 7 kg
Viscosidade do ar a (46ºC)
µ ar := 185⋅ 10
Número de Prandtl do ar (46ºC)
Prar := 0.707
Viscosidade da água (120ºC)
µ aq := 200⋅ 10
Número de Prandtl da água (120ºC)
Praq := 1.24
m⋅ s
− 6 kg
m⋅ s
103
A expressão geral para o coeficiente global de troca térmica é:
1
1
Uc⋅ A c
η 0c⋅ h c⋅ A c
+
Rfc
η 0c⋅ A c
+ Rw +
Rfh
η 0h⋅ A h
+
1
η 0h⋅ h h⋅ A h
O índice "c" indica o fluido frio e "h" o fluido quente
Uc =coeficiente global de troca térmica referido à área do lado do fluido frio
Ac =área da superfície de troca térmica do lado do fluido frio
hc =coficiente de convecção do lado do fluido frio
η 0c =eficiência da aleta do lado fluido frio
Rfc=resistência à condução por incrustação do lado do fluido frio
Rw =resistência à condução da parede do tubo
Ah=área da superfície de troca térmica do lado do fluido quente
hh=coficiente de convecção do lado do fluido
quente
η 0h=eficiência da aleta do lado fluido quente
Rfh=resistência à condução por incrustação do lado do fluido quente
Com a água quente no interior dos tubos e o ar úmido no exterior aletado tem-se:
Não há aletas no interior do tubo: η 0h=1
Admitindo que não há incrustações: Rfc=Rfh=0
Resulta:
1
1
Uc
η 0c⋅ h c
1
+ A c⋅ Rw +
 Ah 

 Ac 
hh⋅ 
Adotada a seguinte configuração para o trocador de calor:
Tubo diâmetro interno D i=22 mm, diâmetro externo D o=26mm
Aletas diâmetro externo D
al =44,1
mm, espessura t=0,304 mm
Superfície CF-8.8-1.0J de Kays, W. M.; London, A. L. Compact Heat Exchangers
Cálculo da resistência térmica da parede do tubo, termo A
Do := 26.0mm
A h_c :=
Di
Do
Di := 22.0mm
⋅ ( 1 − 0.830)
 Do 
Di⋅ ln

 Di 
Rtubo :=
2⋅ kal⋅ A h_c
c Rw =Rtubo
A h_c = 0.144
−5 2 K
Rtubo = 5.368 × 10
m⋅
W
104
Cálculo do coeficiente de convecção do lado do gás
2
Área frontal do TC (perpendicular ao fluxo de gás)
A fr := 2m⋅ 0.4m
A fr = 0.8m
Razão entre a área de escoamento e a área frontal
σ := 0.439
mgv
G :=
σ⋅ A fr
fig 11.20 Incropera
kg
mgv = 4.2
s
Vazão mássica por m2
Diâmetro hidráulico Dh=4Ac/P
Número de Reynolds
G = 11.959
G⋅ Dh
Re = 3794.6
µ ar
Fator de Colburn
2
ms
fig 11.20 Incropera
Dh := 5.87mm
Re :=
kg
jh := 0.0085 −
jh = 0.00671
Coeficiente de convecção do lado do gás
h c := jh ⋅
Re − 2000
G⋅ cp 0
2
Prar
2000
fig 11.20 Incropera
⋅ 0.002
h c = 114.3
3
W
2
m ⋅K
Cálculo da eficiência da aleta
Raio maior da aleta
44.1
r2 :=
mm
2
r2 = 22.05mm
Raio menor da aleta
26
r1 := mm
2
r1 = 13mm
Largura da aleta
L := r2 − r1
L = 9.05mm
Espessura da aleta
t := 0.304mm
Eficiência da aleta η f , cf fig. 3.19 Incropera
t
r2c := r2 +
r2c = 22.2mm
2
t
Lc := L +
Lc = 9.2mm
2
A p := Lc⋅ t
2
A p = 2.8mm
1
3
Com:
2
 hc 
Lc ⋅ 
 = 0.366
 kal⋅ A p 
2
Eficiência global da superfície aletada
Área das aletas / área total (R
(
η 0c := 1 − Raletas_total ⋅ 1 − η f
)
r2c
r1
= 1.7
da fig 3.19:
η f := 92%
η0
aletas_total )
Raletas_total := 0.825
fig 11.20 Incropera
η 0c = 0.934
105
Cálculo do coeficiente de convecção do lado do líquido
Para uma estimativa do número de tubos do TC será calculada a área de troca admitindo para
o coeficiente global de troca térmica metade do valor do coeficiente do lado do gás.
hc
Uc :=
2
A c :=
W
Uc = 57.2
2
m ⋅K
UA
2
A c = 30.8m
Uc
Área total de troca por metro de tubo:
A cm := 2⋅ π⋅  r2c − r1

Quantidade de tubos consideranto 2m de comprimento:
− 4 kg
Di = 0.022m
µ aq = 2 × 10
ms
(
Como Re crítico = 2300,
Reaq :=
)
Nuaq Reaq :=
2
 ⋅ 346⋅ 0.825
n :=
A cm = 0.8536m
Ac
n = 18
A cm⋅ 2
maq
maq_tubo :=
n
kg
maq = 1.432
s
Vazão por tubo:
1
2
2
kg
maq_tubo = 0.0793
s
4⋅ maq_tubo
π⋅ Di⋅ µ aq
Reaq = 22958.6
4.36 if Reaq < 2300
 0.023⋅ Re 0.8⋅ Pr 0.4  otherwise
aq
aq 

(
)
Nuaq Reaq = 77.242
kaq
h h := Nuaq Reaq ⋅
Di
(
)
h h = 2415.6
Relação de áreas nos lados quente e frio A
h
W
2
m ⋅K
/ A c = A h_c
A h_c = 0.144
Given
1
Uc
1
1
+ Rtubo +
h h ⋅ A h_c
η 0c⋅ h c
(
( )
Uc := Find Uc
A c :=
UA
Uc
Quantidade de tubos
)
W
Uc = 81.3
2
m ⋅K
UA = 1761
W
K
2
A c = 21.7m
n :=
Ac
A cm⋅ 2
n = 12.7
106
Cálculo do U c com a nova quantidade de tubos n
n := 13
maq
maq_tubo :=
n
kg
maq = 1.432
s
Vazão por tubo:
− 4 kg
Di = 0.022m
µ aq = 2 × 10
4⋅ maq_tubo
Reaq :=
ms
kg
maq_tubo = 0.1102
s
π⋅ Di⋅ µ aq
Reaq = 31875.5
Como Re crítico = 2300, o escoamento é turbulento
Como Re crítico = 2300,
(
)
Nuaq Reaq :=
4.36 if Reaq < 2300
 0.023⋅ Re 0.8⋅ Pr 0.4  otherwise
aq
aq 

(
)
Nuaq Reaq = 100.43
kaq
h h := Nuaq Reaq ⋅
Di
(
)
h h = 3140.7
Relação de áreas nos lados quente e frio A
h
W
2
m ⋅K
/ A c = A h_c
A h_c = 0.144
Given
1
Uc
1
1
+ Rtubo +
h
A
⋅
η 0c⋅ h c
h
h_c
(
( )
Uc := Find Uc
A c :=
UA
Uc
Quantidade de tubos
)
W
Uc = 86
2
m ⋅K
2
A c = 20.5m
n :=
Ac
A cm⋅ 2
n = 12
Nota: Usou-se o software Mathcad para o cálculo, as abreviaturas sofreram modificação devido à limitação do
software.
107
ANEXO 3 – Diagramas de bloco no Simulink
[Qliq]
[mgs]
From76
From67
[Rar]
From31
[T]
Product34
From68
1
T1
[T]
Integrator
From26
1
s
[T0]
From64
[T]
Temperatura
[Cp0ar]
From65
Product28
Product30
Goto20
[mge]
From29
[Tponto]
In1 Out1
T
K p/ºC10
To Workspace
[Mg]
[R0ar]
From30
From27
[T]
[Cvar]
Product27
Product29
From28
From25
[mge]
From138
[mAP]
From23
RA
Product25
RA1
[T]
From66
Scope73
[W0]
From43
[mge]
From44
Product38
[mAP]
[Mg]
From45
From46
Scope89
1
s
[W]
Integrator2
Umidade do Ar
Product39
[Wponto]
Goto26
w
To Workspace2
108
1
[T]
P1
From42
Integrator1
[Rar]
1
s
Product37
Product24
From41
[P]
Pressão
[Tponto]
V
From70
RA5
P
[P]
[mge]
From40
Product26
From69
RA
[T]
RA2
From71
[mgs]
To Workspace1
[P]
Product32
From24
From72
[Wponto]
From73
[Rar]
From74
Taqe
Temp entr agua quente
1
Taqs
[Te]
[maq]
maq1
Caq
Calor esp agua quente
Product41
From48
Mm
1
s
[TT]
Massa do metal
Integrator4
From49
Cm
Calor específico
Product43
do metal
[mgte]
[Taqs]
Temp de saida da
agua quente
Product45
From50
[CpTear]
From51
Product42
Maq
Massa de agua quente
Caq
Calor específico
de agua quente Product44
109
[T ]
From152
[Te]
From151
[cp_we_w]
From143
[W]
From144
Product91
1
mgv
18
CpA8
Product87
[T 0]
From157
[f]
[T e]
From145
From156
[cp_we_w0]
From153
[W0]
From154
Product93
1
19
[mge]
Product92
From158
Integrator3
1
s
[W]
From167
Product103
1
23
Product98
mgv
[Mg_Te]
CpA12
From172
[Cvar_Te]
[we]
From173
From165
1
22
[Te]
Goto32
Product97
[mgte]
From166
[W]
From155
1
21
Product96
[mgs]
From163
[W0]
[Rar_Te]
From162
From159
1
20
Product95
[mge]
[Te]
Product94
From161
From164
110
[W]
From176
Product104
[we]
From174
mgv
CpA13
[W]
Integrator5
From178
Product105
[we]
From177
1
s
[we]
Goto33
[mgs]
From175
[W0]
From181
Product106
[we]
From180
[mge]
From179
111
ANEXO 4 – Painel de controle no Simulink
112