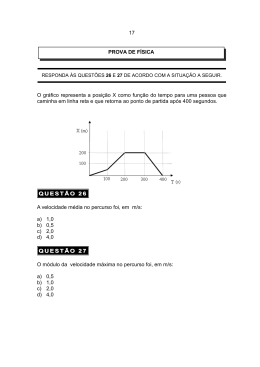
.
UTILIZAÇÃO DE AUTÔMATOS CELULARES
PARA GERAÇÃO DE MÚSICA COMPUTACIONAL
Rafael Rodrigues Lopes (IC)1 , Marcos Antonio Botelho & José Carlos Papa
Labmat
Laboratório de Experiências em Matemática
Departamento de Matemática
Instituto Tecnológico de Aeronáutica
12.228-900 São José dos Campos SP Brazil
[email protected] , [email protected] , [email protected]
RESUMO
Este trabaho apresenta uma forma de se fazer corresponder a autômatos celulares um sistema computacional que pode ser usado na composição musical e
nos estudos sobre a fenomenologia da música.
ABSTRACT
Here we introduce a way to correspond to celular automata a computational
system that can be applied either to the process of composition of musical pieces
or to the study of the phenomenology of music.
Palavras-chave: Sistemas dinâmicos; autômatos celulares; música computacional.
1 INTRODUÇÃO
Ciência (em particular, Matemática) e música podem ser tratados como objetos correlacionados e cada um destes objetos pode se beneficiar desta relação de várias formas. Por
exemplo, podemos usar esta relação como estratégia para a execução de processos de
composição musical ou usá-la para o estudo do processo cognitivo envolvido na expressão
musical e na fenomenologia da percepção. O presente trabalho procura fornecer subsídios para estes dois aspectos através da preparação de um sistema computacional calcado
na teoria de sistemas dinâmicos discretos e, em particular, do autômato celular ‘Jogo da
Vida’, capaz de gerar formas musicais computacionalmente. Desta maneira, este programa poderá servir como ferramenta conceitual em investigações futuras na identificação
dos parâmetros que agem na percepção musical, ou poderá ainda ser usado como subsídio
na organização de sons digitais e composição. Ambas estas aplicações estão nos planos de
nossas investigações futuras.
Já é um preceito da Inteligência Artificial que os computadores podem compor música se
programados adequadamente. Podem compor dentro de um certo estilo, imitando aqueles já conhecidos, ou podem ‘criar música’. Claro que esta expressão não está colocada
1
Bolsista do PIBIC/CNPq.
propriamente, uma vez que os computadores não têm as referências culturais, psicológicas
e cognitivas que permitam o aparecimento da criatividade própria dos humanos. Porém,
modelos matemáticos implementados num computador podem gerar novos padrões e ordenações de sons digitais e a isto podemos chamar, num certo sentido, de composição
musical. Este material tanto pode ser considerado como música computacional acabada,
como pode servir de inspiração para um processo criativo de composição pela intervenção
humana, ou ainda, fornecer subsídios para a identificação dos parâmetros que agem na
percepção musical.
2 PRELIMINARES MATEMÁTICAS
Um sistema dinâmico consiste em um conjunto com uma estrutura (por exemplo, um superfície, um espaço métrico ou um espaço vetorial normado) e uma regra que estabelece
a lei segundo a qual cada elemento é mapeado – ou se ‘move’– neste espaço. Este dinamismo é representado como sendo mudança de estado e por estado entendemos uma
especificação das informações consideradas relevantes para se caracterizar o modelo (exemplos de estado seriam, por exemplo, a posição e a velocidade de um veículo, ou as
coordenadas de um ponto no plano x-y). Um espaço de estados é o conjunto de todos os
valores de estados possíveis para um determinado sistema.
De maneira mais precisa, podemos caracterizar um sistema dinâmico (em tempo) discreto
como sendo um par (f, M) onde M é um espaço de estados e f é uma aplicação f : M → M
considerada junto com suas compostas
f o = id , f 1 = f , f 2 = f ◦ f , f 3 = f ◦ f ◦ f , · · ·
onde id representa a função identidade id M → M dada por id(x) = x. Note que, com
isto, nosso sistema dinâmico discreto é uma família parametrizada {f k : M → M ; k =
0, 1, 2, . . .} tal que
f o = id e f k+m = f k f m = f k ◦ f m
Assim, dado qualquer x ∈ M , a seqüência
xo = x
x1 = f (x)
x2 = f (x1 ) = f(f(x)) = f 2 (x)
..
.
xk+1 = f(xk ) = f k+1 (x)
..
.
determina como a condição inicial xo = x varia em M sob a ação da aplicação sucessiva
da ‘regra’ f . A expressão xk+1 = f(xk ) = f k+1 (x) indica que o estado xk+1 , para o qual
a condição inicial é mapeada no tempo t = k + 1, depende do estado no tempo t = k.
Via de regra, um aspecto a ser analisado é o comportamento do sistema a longo prazo, o
que é idealizado matematicamente através do estudo do comportamento da seqüência (xk )
quando k → ∞, no caso em que o espaço de estados está imbuído de uma estrutura que
permita falar em aproximação e convergência, como ocorre quando M = R ou Rn . Várias
situações podem ser verificadas neste caso: a seqüência pode crescer indefinidamente em
valor absoluto, ou o sistema acabar oscilando entre dois ou mais estados (os quais são
chamados de pontos periódicos), a seqüência pode convergir para um determinado estado.
Uma das classes mais simples de sistemas dinâmicos discretos é a dos autômatos celulares.
Os aspectos que caracterizam esta classe específica são o tipo de espaço de estados e a
forma da regra de transição de estados. Mais especificamente, os ingredientes-chave destes
sistemas no contexto em que estaremos aqui considerando são:
Espaço de estados celular. A dinâmica evolve numa grade de células, normalmente
uma partição retangular do Rn . No caso unidimensional (n = 1), as células consistem em
pontos reticulados na reta. No caso do R2 , que será o cenário deste trabalho, o espaço de
estados é uma estrutura de quadrados como num tabuleiro de xadrez infinito.
Estados finitos. Cada célula do espaço de estados pode assumir apenas um número
finito K de valores diferentes, de forma que numa grade finita constituída de N células, o
número total de estados possíveis é K N .
Sistemas determinísticos. A regra que determina o valor de cada célula é uma função
determinística (em oposição aos processos estocásticos) do valor corrente desta célula e
dos valores das células em alguma vizinhança desta célula.
Homogeneidade. Cada célula do sistema pode assumir exatamente o mesmo conjunto
de K valores possíveis em cada momento e a mesma regra de transição é aplicada a cada
célula.
Localidade. As transições de estado são locais tanto no espaço quanto no tempo. Mais
especificamente, o valor a ser assumido por uma célula dada depende somente do valor
corrente desta célula e dos valores no momento anterior das células numa sua vizinhança.
No caso de um autômato unidimensional, uma vizinhança consiste num número finito de
células em cada lado de uma célula dada.
Para autômatos bidimensionais, existem várias possibilidades não equivalentes de vizinhança, sendo que dois tipos de interesse no nosso estudo são:
1. Vizinhança de von Neumann: consiste das células vertical e horizontalmente adjacentes
à célula dada.
1. Vizinhança de Moore: consiste das células vertical, horizontal e diagonalmente adjacentes à célula dada.
A regra de transição de estado na célula (i, j) no caso da vizinhança de von Neumann, por
exemplo, tem a forma
´
³
(k+1)
(k) (k)
(k)
(k)
(k)
= φ ai,j , ai,j+1 , ai+1,j , ai,j−1 , ai−1,j
ai,j
Um tipo de regra, chamada de regra totalística, é aquela na qual o valor de uma célula
no tempo k + 1 depende somente da soma dos valores das células no tempo k. Para se
ter uma indicação do espectro de possibilidades das regras de transição nos autômatos
bidimensionais, basta notar que para K = 2 valores por célula, existe no caso de regras
gerais um total de 232 regras para a vizinhança de von Neumann e uma queda drástica
para 25 regras totalísticas. Para a vizinhança de Moore, os números correspondentes
são ainda maiores: 2512 regras gerais e 29 regras totalísticas. Isto dá uma idéia da impossibilidade de explorar computacionalmente as propriedades e os comportamentos de
todas as regras. Porém, algumas características que puderam ser constatadas através
de alguns experimentos computacionais com autômatos bidimensionais. Uma delas é que
estes processsos frequentemente geram padrões dendríticos, caracterizados por dimensões
topológicas de crescimento não-inteiras, e que certas questões permanecem formalmente
indecidíveis, como por exemplo se uma configuração particular pode ser gerada depois de
um único passo temporal a partir de uma configuração inicial, ou se existem configurações
que têm um período temporal particular e são consequentemente invariantes para um certo
número de interações da regra do autômato.
O autômato que será usado no presente estudo é o autômato bidimensional conhecido
como ‘Jogo da Vida’, que usa a vizinhança de Moore com a seguinte regra de transição de
estado, criada por John Horton Cornway (v. Gardner[3]):

P
(k)

ai,j , se

n an = 2




P
(k+1)
=
ai,j
1
, se
n an = 3





 0
, caso contrário.
P
onde a notação n an representa a soma de todas as células na vizinhança de Moore da
célula (i, j).
3 SOBRE O CÓDIGO COMPUTACIONAL
Para a criação e cálculo das várias gerações do autômato Jogo da Vida, foi desenvolvido um
programa em linguagem C++. Para a geração do arquivo musical, fez-se uso do programa
CSOUND, um programa de domínio público de síntese sonora desenvolvido no MIT que
possibilita a criação de som a partir de vários osciladores e filtros que podem ser totalmente
modificados pelo usuário. O programa possui dois arquivos de entrada básicos. O primeiro
deles é o arquivo da orquestra (orchestra). Neste arquivo são definidas características como
a qualidade sonora (sampling rate) e número de canais, além de serem definidos todos os
instrumentos que serão utilizados na geração do arquivo sonoro. Este arquivo pode ser
criado em qualquer editor de texto, e deve ter a extensão .orc. O segundo arquivo é a
partitura (score). Neste, são dispostas as funções correspondentes às ondas sonoras e a
relação de todas as notas tocadas com suas respectivas características, como o instrumento
que a toca, o instante em que ela é tocada, sua duração, freqüência e amplitude. Este
arquivo também pode ser criado em qualquer editor de texto e possui a extensão .sco.
Utilizando estes arquivos de entrada, o programa gera um arquivo sonoro de extensão
.wav, que pode ser reproduzido em um programa adequado.
O programa em C++ desenvolvido possui um arquivo de saída do tipo .sco com as informações necessárias ao programa CSOUND para a geração do arquivo sonoro desejado.
Antes de se gerar os arquivos sonoros, fez-se necessária a construção de um código computacional que empregasse as regras do Jogo da Vida. Para isso, utilizou-se a linguagem C++,
tendo como parâmetros de entrada do programa as dimensões do diagrama bidimensional,
o estado inicial (geração 0) e o número de gerações desejadas. A partir dessas condições,
o programa calcula as várias gerações, mostrando os resultados na tela do computador e
gravando-os no arquivo “geracoes.txt ”.
Ainda, de acordo com as regras de criação de som definidas mais adiante, o programa
cria automaticamente os arquivos compatíveis com o software CSOUND, utilizados para
geração da música.
Optou-se, na implementação das regras do Jogo da Vida no programa, por não aplicá-las
às células pertencentes às bordas do diagrama bidimensional. Tendo em vista o fato que
a vizinhança dessas células é incompleta, decidiu-se por manter seus valores inalterados
em todas as gerações. Ou seja, os estados das bordas são os mesmos da condição inicial
ao longo de toda a simulação. Apesar de não se submeterem às regras do autômato, as
células das bordas influenciam o estado de suas vizinhas que não pertencem às bordas.
Por este motivo, optou-se por não considerar as células das bordas na criação do som. Por
exemplo, caso tomemos um diagrama de 20 células por 15 células, teremos um diagrama
“efetivo” na criação de som composto por 18 × 13 células.
4 REGRAS PARA A CRIAÇÃO DO SOM
Tendo em vista as inúmeras possibilidades de associação do autômato celular à criação de
som, decidiu-se pelo estudo e desenvolvimento de várias regras de associação diferentes.
Desta forma, torna-se possível uma maior vesatilidade no que tange a composição musical.
É possível utilizar, por exemplo, uma superposição de uma melodia criada com uma regra
e uma forma de onda criada com outra regra. Assim, as possibilidades para um compositor
utilizando essas diferentes regras torna-se bem extensa.
Primeira Regra. A primeira regra desenvolvida baseou-se apenas na criação de uma
linha melódica. Para isto, utilizou-se o instrumento mais simples possível: um oscilador
senoidal. O diagrama foi definido como possuindo 14×12 células. Desta forma, o diagrama
“efetivo ” é composto por 12 × 10 células, sendo que as 12 linhas de células representam as
12 notas que compõem uma oitava. A primeira linha representa o dó central (f = 256Hz)
e a última representa o sí da mesma oitava (f = 483Hz). As freqüências intermediárias
foram determinadas seguindo a relação f(n) = f(0) · (0, 05946)n . Aqui, n equivale ao
intervalo em semitons em relação a uma nota base. Em nosso caso, tomando o dó central
como base, teremos: f(n) = 256 · (0, 05946)n . Portanto, caso desejemos obter a freqüência
da nota sol (7) em relação ao dó, obteremos f = 384Hz. É fácil perceber que, caso
tomemos um semitom acima da nota si, teremos o dó da próxima oitava (f = 512Hz),
que corresponde, exatamente, ao dobro do valor da freqüência do dó central.
O programa começa lendo a coluna mais à esquerda do diagrama e lê uma coluna do
diagrama por vez. Cada vez que este encontra uma célula ligada (Valor = 1), escreve no
arquivo de saída o equivalente a uma nota com a freqüência correspondente à linha em
que esta célula se encontra. A duração de cada nota é de 0,2 segundos. Ao final da coluna,
o programa soma 0,2 segundos ao tempo decorrido da música e começa a ler a próxima
coluna. Ao final do diagrama, o programa calcula a próxima geração e continua o processo
até que o número de gerações termine.
Finalmente, o operador deve tomar o arquivo “score.sco” gerado e rodar o programa
CSOUND utilizando este arquivo como parâmetro de entrada.
Observou-se que, utilizando-se esta regra, os resultados se mostraram com uma característica interessante. Os arquivos gerados, em geral, possuíam um início um tanto confuso e
destoante, com muitas notas sendo tocadas simultaneamente. Após os primeiros segundos,
possuíam uma melodia composta de uma ou duas notas sendo tocadas a cada instante e
com algumas pausas entre as notas. Provavelmente, uma forma de se melhorar os resultados obtidos seria, por exemplo, forçar apenas uma nota a ser tocada de cada vez e retirar
as pausas.
Segunda Regra. A metodologia utilizada na segunda regra é uma evolução da primeira.
A associação de cada coluna a uma respectiva nota dentro da oitava se apresenta da mesma
forma que na regra descrita anteriormente. A diferença desta regra para a primeira está no
intervalo entre notas tocadas. Neste, o programa inicia a leitura do diagrama a partir da
extremidade superior esquerda, e realiza o procedimento coluna por coluna. A cada célula
encontrada ligada, o programa associa a freqüência correspondente. O contador de tempo,
porém, passa para o instante correspondente ao final da nota que acabou de ser criada.
Desta forma, não há mais que uma nota sendo tocada em cada instante. Ainda, neste caso,
o contador não sofre incremento quando o programa atinge o final da coluna, deixando
para fazê-lo apenas ao final de cada nota tocada. Pelo mesmo motivo, não existem pausas
entre as notas tocadas.
Utilizando-se esta regra obtêm-se melodias muito mais familiares aos ouvintes. A grande
quantidade de sons diferentes presentes no início das músicas geradas com a regra anterior
não aparece neste caso. Além disso, as grandes pausas características das músicas do
primeiro caso também não se fazem presentes aqui. O resultado é uma melodia contínua
e abstrata, mas capaz de produzir sensações agradáveis ao ouvinte.
Terceira Regra. As possibilidades de regras para associação não se limitam à criação de
linhas melódicas, apesar de esta se apresentar a mais direta. Pelo contrário, as possibilidades de associação são inúmeras, dependendo apenas da disponibilidade de tempo e da
criatividade do aluno. Há possibilidade de se realizar associações com o ritmo da música,
com os timbres dos sons, com a harmonia , intensidades, ou com uma combinação de vários
fatores, para citar alguns casos possíveis. Tendo em vista o exposto acima, a terceira regra
de associação usada baseia-se numa abordagem bem diferente das duas primeiras. Desta
vez, as várias gerações do Jogo da Vida são associadas a variações do timbre sonoro, sem se
preocupar com a melodia. Para isso, utilizou-se dois osciladores, um deles sendo o mesmo
dos casos anteriores, um oscilador senoidal e o outro, por sua vez, sendo um oscilador com
forma de onda do tipo “dente de serra”. O timbre sonoro correspondente a essa forma
de onda é bem reconhecível, caracterizado por um som metálico. O diagrama utilizado
neste caso possui as mesmas dimensões que os diagramas utilizados para a implementação
das outras regras. A cada linha do diagrama, associou-se uma intensidade diferente de
cada oscilador, da seguinte forma: A primeira linha corresponde ao primeiro oscilador
(senoidal) tocando e o oscilador “dente de serra” desligado. A última linha corresponde
ao primeiro oscilador (senoidal) desligado e o oscilador “dente de serra” tocando. Nas outras linhas, os dois osciladores estão ligados, mas a intensidade de cada um varia de forma
equivalente, de acordo com a posição no diagrama. Desta forma, uma célula próxima à
primeira linha corresponde a uma grande intensidade do oscilador senoidal e uma pequena
intensidade do oscilador “dente de serra”, e vice-versa. Próximo ao centro do diagrama, os
osciladores possuem valores de intensidade próximos. Teve-se a preocupação de se manter
a intensidade total igual para todos os casos.
O programa inicia a leitura do diagrama, novamente, da extremidade superior esquerda,
ao longo da primeira coluna, da mesma forma que o caso anterior. A diferença é que a nota
tocada é sempre a mesma, o lá correspondente à freqüência f = 440Hz. Assim, observa-se
a enorme diferença de resultados desta regra para as regras anteriores. As músicas geradas
com esta regra são caracterizadas pela ausência de uma linha melódica, em favor de uma
maior riqueza nos timbres envolvidos.
4 CONCLUSÃO
A possibilidade de se utilizar a criatividade para gerar novas regras é inesgotável. Por
exemplo, pode-se mesclar os resultados das regras dois e três, realizando-se um código que
associasse as diferentes colunas a diferentes notas musicais e as linhas a diferentes formas
de onda, ou vice-versa. Com isto, pode-se esperar a obtenção de resultados mais ricos em
termos musicais que os observados nos três casos descritos anteriormente. Ooutra linha
possível seria a criação de outras regras de associação diferentes. Desta forma, aumentarse-ia a variedade de sons criados, tornando mais rica uma futura composição que fizesse
uso dos resultados deste trabalho.
Um aspecto importante deste trabalho é a percepção que os resultados aqui obtidos muito
provavelmente não têm importância musical significativa por si só. Entretanto, possuem
uma utilidade considerável se utilizados como ferramentas nas mãos de um compositor.
É possível construir uma peça musical mesclando-se vários trechos de sons de diferentes
características a partir dos autômatos celulares. A qualidade musical da peça dependerá,
é claro, da experiência do músico como compositor, da familiaridade dele com o processo
de criação envolvido e, ainda, de sua inspiração no momento da composição.
REFERÊNCIAS
[1] Casti,J.L.: Reality rules. Picturing the world in mathematics. Vol. II. John Wiley &
Sons, 1992.
[2] Miranda, E.R.: On the music of emergent behaviour. What can evolutionary computation bring to the musician? Sony Computer Science Laboratory, Paris.
[3] Gardner, M: Wheels, Life and Other Mathematical Amusements. Freeman, San Francisco, 1983.