3
Lógicas Temporais para a Validação de Sistemas
Neste capítulo apresentamos diversas lógicas que têm sido utilizadas
PUC-Rio - Certificação Digital Nº 0310848/CB
para a validação de sistemas. Do ponto de vista prático, a validação ocorre,
tipicamente, através de duas abordagens: a verificação de modelos (model
checking) (CGP99), na qual o sistema e a propriedade a ser validada são
representados, respectivamente, como um modelo, geralmente finito, e uma
fórmula da lógica; e a prova automática de teoremas (automated theorem
proving) (Fit96), na qual tanto o sistema como a propriedade são representadas
como fórmulas da lógica. Diversas linguagens lógicas têm sido utilizadas para
ambas as abordagens a exemplo da lógica proposicional, da lógica de primeiraordem, e das lógicas modais e temporais, entre outras. Cada abordagem possui
as suas vantagens e desvantagens. Vale ainda ressaltar que essas duas técnicas
podem ser combinadas para a validação de sistemas.
Abaixo iremos declarar o problema da verificação de modelos e da prova
automática de teoremas para lógicas em geral. A partir daí, apresentamos as
lógicas temporais: full Computation Tree Logic (CTL*) (EH86); Computation
Tree Logic (CTL) (CE81); e Linear Temporal Logic (LTL). A lógica µ-calculus,
que expressa CTL e LTL, não será apresentada neste capítulo. Em particular,
estaremos mais interessados neste trabalho na lógica CTL, que é base da lógica
proposta neste trabalho. Por fim, esboçaremos a verificação de modelos para a
lógica CTL através do verificador de modelos Symbolic Model Verifier (SMV)
(McM93).
Em verificação de modelos se está interessado em procedimentos ‘eficientes’ que decidam se uma fórmula α, que representa uma propriedade do
sistema, é satisfeita (|=) na estrutura G, geralmente finita, que representa o
sistema. Uma formulação geral para o problema de verificação de modelos é
introduzido como:
G |= α
A técnica de verificação de modelos (model checking) (CGP99) é freqüentemente aplicada na ciência da computação para a validação de software e
hardware (BCL91). Esta técnica consiste na verificação automática de propriedades acerca do comportamento de sistemas através de enumeração exaustiva
Capítulo 3. Lógicas Temporais para a Validação de Sistemas
58
de todos os estados alcançáveis. Diversas implementações estão disponíveis na
literatura, tais como o Symbolic Model Verifier (SMV) (McM93) e o SPIN
(Hol97). Algumas outras também incluem características especificas na sua
modelagem: UPPAAL (BLL+ 95) trata de tempo-real; HYTECH (HHWT95)
de autômatos híbridos; e o PRISM (Par02) de autômatos estocásticos. Recentemente, a verificação de modelos vem sendo empregada na verificação de
propriedades de jogos (Vas03, BSWZ01, vOvdHW04, vdHW02, KP04).
Embora a uma primeira vista esta abordagem pareça simples, a exemplo
PUC-Rio - Certificação Digital Nº 0310848/CB
da lógica proposicional, veremos que este problema para algumas lógicas pode
ser uma tarefa difícil. Para algumas lógicas a complexidade para determinar
se uma fórmula é satisfeita em uma estrutura é P SP ACE-completo.
A outra abordagem que vem sendo aplicada em ciência da computação é a
de provas automáticas de teoremas (automated theorem proving) (Fit96), onde
utiliza-se de uma linguagem lógica para representar o sistema e a propriedade
que se deseja verificar, então utiliza-se um método de prova (cálculo dedutivo)
para verificar a correção da propriedade de forma automática. Diversos cálculos
dedutivos têm sido desenvolvidos, tais como axiomático (ou à la Hilbert),
dedução natural, cálculo de sequentes, tableaux, resolução, entre outros. Cada
um dos sistemas têm as suas vantagens e desvantagens.
Sejam Γ e α um conjunto finito de fórmulas e uma fórmula, respectivamente, de uma lógica com um sistema de prova K. Então uma formulação
geral para o problema de prova de teoremas é introduzido como:
Γ !K α
Este problema está relacionado ao problema de determinar se um
conjunto de fórmulas Γ ∪ {¬α} é insatisfatível, i.e., se não existe uma estrutura que satisfaz todas as fórmulas de Γ ∪ {¬α}. Para lógica proposicional,
por exemplo, o problema da satisfatibilidade é NP-Completo e o da prova de
teoremas é, então, CoNP-Completo. Além da dificuldade de resolver este problema para algumas lógicas, temos que este problema é indecidível, a exemplo
da lógica de primeira-ordem.
Apesar disso, existe muita pesquisa na área de prova automática de
teoremas, e existem diversos provadores automáticos de teoremas disponíveis
na literatura. Os provadores Otter (Kal01), SPASS(Wei97), Vampire (RV02) e
Waldmeister (THL97) usam lógica de primeira-ordem, enquanto os provadores
ACL2 (MKM00), e HOL (Age94) usam lógica de alta-ordem.
Capítulo 3. Lógicas Temporais para a Validação de Sistemas
59
3.1
Lógicas Temporais
Lógicas temporais foram introduzidas por filósofos para o estudo da
relação com o tempo, possuindo assim operadores temporais, a exemplo
dos operadores de F e P , que expressam futuro e passado, respectivamente. Recentemente, diversas lógicas temporais têm sido utilizadas para
a validação de propriedades acerca do comportamento de sistemas reativos
(Pnu77, CGP99, Hol97). Sistemas reativos têm como caracterização básica
estados e transições. Estado é a descrição do sistema em um dado instante
de tempo, ou seja, os valores associados as suas variáveis naquele instante.
Transição é uma relação entre dois estados. Chamamos de computação uma
PUC-Rio - Certificação Digital Nº 0310848/CB
seqüência infinita de estados, onde cada estado é obtido através de um estado
anterior e uma relação de transição entre eles.
A interpretação de lógicas temporais se dá, tradicionalmente, através
de estrutura de Kripke, que captura a intuição do comportamento de um
sistema reativo. Uma estrutura de Kripke é um conjunto de estados, um
conjunto de transições entre estados e uma função, que rotula cada estado
com o conjunto de propriedades verdadeiras nele. Caminhos em estrutura de
Kripke são computações em sistemas reativos. Deve-se ainda considerar que
existe uma restrição na abordagem lógica: as relações de transições devem
ser totais. As estruturas de Kripke são simples e suficientes para capturar os
aspectos mais relevantes do comportamento dos sistemas reativos.
A definição formal de estrutura de Kripke para lógica temporal é apresentada abaixo. A figura 3.1 apresenta uma representação da estrutura de Kripke
apresentada no exemplo 3.2, que tem um caráter apenas ilustrativo.
Definição 3.1 Uma estrutura de Kripke é definida por #S, So , R, L$, onde
– Um conjunto não-vazio de estados S.
– Um conjunto de estados iniciais So ⊆ S.
– Uma relação R ⊆ S × S total1 , i.e., para todo estado s ∈ S existe um
estado s! ∈ S tal que #s, s! $ ∈ R.
– Uma função de rótulos L : S → 2Π , onde Π é o conjunto de proposições.
Exemplo 3.2 Exemplo de uma estrutura de Kripke K3.2 = #S, So , R, L$, onde
– S = {s, sa , sab }.
– So = {s}.
1
A restrição da relação R ser total é válida para lógicas temporais. Vale ressaltar que
diversas outras lógicas modais não possuem esta restrição.
Capítulo 3. Lógicas Temporais para a Validação de Sistemas
60
– #s, sa $ ∈ R, #sa , s$ ∈ R, #s, sab $ ∈ R, #sa , sab $ ∈ R, #sab , sab $ ∈ R.
– L(s) = ∅, L(sa ) = {a}, L(sab ) = {a, b}.
Um caminho em uma estrutura de Kripke a partir de um
estado s ∈ S é uma seqüencia π = s0 , s1 , . . . tal que s = s0 e ∀k ≥
0, #sk , sk+1 $ ∈ R. Referenciamos um caminho começando em um estado s como
um s-caminho. Denotamos πk , π0,k , πk,∞ como o estado sk do caminho π, o
prefixo s0 , s1 , . . . , sk de π e o sufixo sk , sk+1 , . . . de π, respectivamente. Na
estrutura K3.2 temos os seguintes caminhos a partir do estado s: s, sa , s, sa , . . .;
s, sa , s, sa , . . . , sab , sab , . . .; s, sab , sab , . . ..
PUC-Rio - Certificação Digital Nº 0310848/CB
#$
#
"
s
!"
""""
"
"
"" "
" ""
" "
$$
"
%"
#$
#$
a
!
a b
sa
sab
!"
!"
Figura 3.1: Estrutura de Kripke.
As propriedade dos sistemas reativos que desejamos verificar são usualmente divididas em dois tipos: segurança (safety) que expressa que ‘nada ruim
acontecerá’; e progresso (liveness) que expressa que ‘algo bom acontecerá’.
Abaixo apresentamos alguns exemplos destas propriedades.
– Segurança (safety): ‘nada ruim acontecerá’.
– O sistema nunca irá entrar em deadlock.
– Nunca dois processos entram na região crítica ao mesmo tempo.
– Progresso (liveness): ‘algo bom acontecerá’.
– Cada processo irá entrar na região crítica.
– Toda requisição será atendida.
As propriedades a serem verificadas em um sistema reativo são expressas
como fórmulas, que especificam os comportamentos desejados, de uma linguagem lógica temporal.
As lógicas podem ser dividas em lógica temporal de tempo ramificado
e em lógica temporal de tempo linear. Tais lógicas se referem a noção de
seqüências de estados que descrevem possíveis computações do sistema, e não
Capítulo 3. Lógicas Temporais para a Validação de Sistemas
#$
61
!"
"& s
"
&&
#$
#$
""
&
%
"
&
'
a
a b
ab
a
!"
!"
*(
*
(
*
+
)
(
$
#$
#$
#$
s
s
a b
a b
!"
!"
s !"
sab
sab
*(
(
*
)
(
*
+
$
$
PUC-Rio - Certificação Digital Nº 0310848/CB
Figura 3.2: Árvore de Computação Infinita.
a valores de tempos, ou a intervalos de tempos; uma vez que se deseja tratar
de comportamentos de sistemas não-determinísticos que envolvem diferentes
caminhos. Isto é, ou cada estado pode ter vários sucessores em termos de
ramificação, ou o comportamento é dado por um conjunto de caminhos que
são lineares.
Em lógica de tempo ramificado a multiplicidade de comportamentos pode
ser especificada explicitamente por uma propriedade de todos os próximos
estados ou por uma propriedade do próximo estado, enquanto em lógica de
tempo linear, esta multiplicidade é expressa de forma implícita2 .
A seguir iremos apresentar as lógicas CTL* e CTL, que são lógicas de
tempo ramificado, e a lógica LTL, que é um lógica de tempo linear. No fim
desta seção iremos fazer uma breve discussão sobre essas lógicas.
A lógica full Computation Tree Logic (CTL*) descreve propriedades de
árvores de computações, que são obtidas a partir de um estado através do
desdobramento de uma estrutura de Kripke em uma árvore de computação
infinita, como é ilustrado na árvore de computação apresentada na figura 3.2
a partir do estado s da estrutura de Kripke apresentada na figura 3.1.
A linguagem lógica de CTL* é definida em duas partes: uma linguagem
que expressa propriedades de estados como apresentada na gramática Φs a
seguir. Por exemplo, a fórmula Eα significa que existe um caminho tal que a
fórmula α vale, enquanto que a fórmula Aα significa que em todos os caminhos
a fórmula α vale; e uma linguagem temporal como apresentado na gramática
Φp a seguir, expressando propriedades sobre um caminho. Os operadores X
(‘Next time’), F (‘in the Future’), G (‘Globally’) e U (‘Until ’) são lidos da
seguinte forma.
– Xα significa ‘no próximo estado do caminho vale α’.
2
Através do conjunto dos caminhos lineares de uma estrutura.
62
Capítulo 3. Lógicas Temporais para a Validação de Sistemas
– F α significa ‘em algum estado no caminho vale α’.
– Gα significa ‘em todo estado no caminho vale α’.
– αUβ significa ‘vale α no caminho até que vale β’.
&! &! &! &!
%! &! %! %!
α
α
(a) - Xα.
(c) - Gα.
%! %! &! %!
α
α
(b) - F α.
α
α
α
&! &! &! %!
α
β
(d) - (αUβ).
Figura 3.3: Operadores temporais X, F, G e U.
PUC-Rio - Certificação Digital Nº 0310848/CB
Abaixo apresentamos a linguagem e a semântica de CTL*.
Definição 3.3 (Sintaxe de CTL*) Sejam Π um conjunto de letras proposicionais e P ∈ Π uma letra proposicional. A linguagem lógica de CTL* é
gerada pela seguinte BNF:
Φs ::= P | (¬Φs ) | (Φs ∧ Φs ) | (Φs ∨ Φs ) | (Φs → Φs ) | (EΦp ) | (AΦp )
Φp ::= Φs | (¬Φp ) | (Φp ∧Φp ) | (Φp ∨Φp ) | (Φp → Φp ) | (XΦp ) | (F Φp ) | (GΦp ) | (Φp U Φp )
Definição 3.4 (Semântica de CTL*) A definição de satisfação |= de
CTL* é definida em duas partes.
– Se α é uma fórmula da linguagem Φs , escrevemos K |=s α para dizer
que a fórmula α é satisfeita na estrutura K no estado s. A definição de
satisfação é apresentada abaixo.
–
–
–
–
–
–
–
K |=s
K |=s
K |=s
K |=s
K |=s
K |=s
K |=s
P ⇐⇒ P ∈ L(s).
(¬α) ⇐⇒ NÃO K |=s α.
(α ∧ β) ⇐⇒ K |=s α E K |=s β.
(α ∨ β) ⇐⇒ K |=s α OU K |=s β.
(α → β) ⇐⇒ SE K |=s α ENTÃO K |=s β.
(Eα) ⇐⇒ Existe um caminho π a partir de s tal que K |=π α.
(Aα) ⇐⇒ Para todo caminho π a partir de s vale que K |=π α.
– Se α é uma fórmula da linguagem Φp , escrevemos K |=π α para dizer
que a fórmula α é satisfeita na estrutura K no caminho π. A definição
de satisfação é apresentada abaixo.
Capítulo 3. Lógicas Temporais para a Validação de Sistemas
63
K |=π α ⇐⇒ se α é uma fórmula da linguagem Φs , K |=π0 α.
K |=π (¬α) ⇐⇒ NÃO K |=π α.
K |=π (α ∧ β) ⇐⇒ K |=π α E K |=π β.
K |=π (α ∨ β) ⇐⇒ K |=π α OU K |=π β.
K |=π (α → β) ⇐⇒ SE K |=π α ENTÃO K |=π β.
K |=π (Xα) ⇐⇒ K |=π1,∞ α (veja a figura 3.3.a).
K |=π (F α) ⇐⇒ Existe um k ≥ 0 tal que K |=πk,∞ α (veja a figura
3.3.b).
– K |=π (Gα) ⇐⇒ Para todo k ≥ 0 vale que K |=πk,∞ α (veja a figura
3.3.c).
– K |=π (αUβ) ⇐⇒ Existe k ≥ 0 tal que K |=πk,∞ β e para todo
0 ≤ l < k vale que K |=πl,∞ α (veja a figura 3.3.d).
–
–
–
–
–
–
–
Abaixo são apresentadas algumas fórmulas com suas relações de satisfa-
PUC-Rio - Certificação Digital Nº 0310848/CB
ção para o exemplo 3.2.
– K3.2 |=s (E(G(¬b))), que pode ser lido como ‘existe uma caminho a partir
de s tal que sempre não vale b’.
– K3.2 |=s (A(F a)), que pode ser lido como ‘para todos os caminhos a
partir de s no futuro vale a’.
– K3.2 |=s,sab ,sab ,... (F (G(a ∧ b))), que pode ser lido como ‘no caminho
s, sab , sab , . . . vale no futuro que sempre vale a e b’.
– K3.2 1|=s,sa ,s,sa ,... (G a), que pode ser lido como ‘não vale no caminho
s, sa , s, sa , . . . que sempre vale a’.
– K3.2 1|=s (A(G(a ∨ b))), que pode ser lido como ‘não vale para todo
caminho a partir de s que sempre vale a ou b’.
Duas lógicas que estão contidas e são diferentes de CTL* são a lógica
Linear-time Temporal Logic (LTL) (Pnu77) e a lógica Computation Tree Logic
(CTL) (CE81), que são interpretados somente sobre caminhos e estados,
respectivamente. A sintaxe e semântica de ambas são apresentadas abaixo,
bem como algumas fórmulas para o exemplo 3.2.
Iremos delimitar os operadores temporais de CTL através de ‘[’ e ‘]’ com o
intuito de deixar claro que temos apenas um operador temporal. Por exemplo,
[EX] é apenas um operador, não podendo ser desmembrado no operador E
ou no operador X como no caso de CTL*. Os operadores de CTL podem ser
lidos como segue.
– [EX]α - ‘existe um caminho tal que no próximo estado vale α’.
– [AX]α - ‘para todo caminho no próximo estado vale α’.
Capítulo 3. Lógicas Temporais para a Validação de Sistemas
64
– [EF ]α - ‘existe um caminho tal que no futuro vale α’.
– [AF ]α - ‘para todo caminho no futuro vale α’.
– [EG]α - ‘existe um caminho tal que sempre vale α’.
– [AG]α - ‘para todo caminho vale sempre α’.
– E(αUβ) - ‘existe um caminho tal que vale α até que vale β’.
– A(αUβ) - ‘para todo caminho vale α até que vale β’.
Definição 3.5 (Sintaxe de CTL) Sejam Π um conjunto de letras proposicionais e P ∈ Π uma letra proposicional. A linguagem lógica de CTL é
gerada pela seguinte BNF:
Φs ::= P | (¬Φs ) | (Φs ∧ Φs ) | (Φs ∨ Φs ) | (Φs → Φs ) | ([EX]Φs ) | ([AX]Φs )
PUC-Rio - Certificação Digital Nº 0310848/CB
| ([EF ]Φs ) | ([AF ]Φs ) | ([EG]Φs ) | ([AG]Φs ) | (E(Φs U Φs )) | (A(Φs U Φs ))
Definição 3.6 (Semântica de CTL) Sejam Π um conjunto de letras proposicionais, P uma letra proposicional em Π, K = #S, So , R, L$ uma estrutura
de Kripke para Π, s ∈ S um estado da estrutura K, e α uma fórmula de CTL.
Escrevemos K |=s α para indicar que a fórmula α é satisfeita no estado s da
estrutura K. A definição de satisfação |= é como segue.
– K |=s P ⇐⇒ P ∈ L(s).
– K |=s (¬α) ⇐⇒ NÃO K |=s α.
– K |=s (α ∧ β) ⇐⇒ K |=s α E K |=s β.
– K |=s (α ∨ β) ⇐⇒ K |=s α OU K |=s β.
– K |=s (α → β) ⇐⇒ SE K |=s α ENTÃO K |=s β.
– K |=s ([EX]α) ⇐⇒ Existe um caminho π a partir de s tal que K |=π1 α
(veja a figura 3.4.a).
– K |=s ([AX]α) ⇐⇒ Para todo caminho π a partir de s vale que K |=π1 α
(veja a figura 3.4.b).
– K |=s ([EF ]α) ⇐⇒ Existe um caminho π a partir de s tal que existe um
k ≥ 0 tal que K |=πk α (veja a figura 3.4.c).
– K |=s ([AF ]α) ⇐⇒ Para todo caminho π a partir de s vale que existe
um k ≥ 0 tal que K |=πk α (veja a figura 3.4.d).
– K |=s ([EG]α) ⇐⇒ Existe um caminho π a partir de s tal que para todo
k ≥ 0 vale que K |=πk α (veja a figura 3.4.e).
Capítulo 3. Lógicas Temporais para a Validação de Sistemas
65
– K |=s ([AG]α) ⇐⇒ Para todo caminho π a partir de s vale que para todo
k ≥ 0 vale que K |=πk α (veja a figura 3.4.f ).
– K |=s (E(αUβ)) ⇐⇒ Existe um caminho π a partir de s tal que existe
k ≥ 0 tal que K |=πk α e para todo 0 ≤ l < k vale que K |=πl α (veja a
figura 3.4.g).
– K |=s (A(αUβ)) ⇐⇒ Para todo caminho π a partir de s vale que existe
k ≥ 0 tal que K |=πk α e para todo 0 ≤ l < k vale que K |=πl α (veja a
figura 3.4.h).
Assim como em diversas outras lógicas, alguns dos operadores de CTL
são definidos através dos outros. Por exemplo, os operadores ¬, →, [EX], [EG]
e EU definem os operadores ∧, ∨, [AX], [EF ], [AF ], [AG] e AU como abaixo.
Vale ressaltar que existem outros conjuntos de operadores, que expressam os
PUC-Rio - Certificação Digital Nº 0310848/CB
demais operadores.
• α ∧ β ⇐⇒ ¬(α → ¬β)
• α ∨ β ⇐⇒ (¬α) → β
• [AX]α ⇐⇒ ¬[EX](¬α) • [EF ]α ⇐⇒ E(2 U α)
• [AF ]α ⇐⇒ ¬[EG](¬α)
• [AG]α ⇐⇒ ¬[EF ](¬α)
• A(αUβ) ⇐⇒ (¬E((¬β) U (¬α ∧ ¬β))) ∧ (¬[EG](¬β))
Quando utilizamos CTL, dizemos que o sistema é correto em relação a
uma propriedade se a propriedade é satisfeita na estrutura, que representa o
sistema, para todos os estados iniciais.
Abaixo são apresentadas algumas fórmulas com suas relações de satisfação para o exemplo 3.2.
– K3.2 |=s ([EG](¬b)), que pode ser lido como ‘existe uma caminho a partir
de s tal que sempre não vale b’.
– K3.2 |=s ([AF ] a), que pode ser lido como ‘para todo o caminho a partir
de s no futuro vale a’.
– K3.2 |=s ([EF ]([AG](a∧b))), que pode ser lido como ‘existe uma caminho
a partir de s tal que no futuro sempre vale a e b’.
– K3.2 1|=s ([EG] a), que pode ser lido como ‘não existe um caminho a
partir de s tal que sempre vale a’.
– K3.2 1|=s ([AG](a∨b)), que pode ser lido como ‘não vale para todo caminho
a partir de s que sempre vale a ou b’.
66
Capítulo 3. Lógicas Temporais para a Validação de Sistemas
)*
'(
*(
*
(
*
(
)*
*
+
) α
(
+
'(
,.
,.
, .
, .
,
.
,
.
)*
)*
,./)*
,./)*
'(
.
..
'(
. '(
.
..
..
)*
(a) - [EX]α
'(
.
..
PUC-Rio - Certificação Digital Nº 0310848/CB
'(
*(
*
(
*
(
)*
)*
*
+
)
(
'(
'(
,.
,.
, .
, .
.
,
.
α ,-,
)*
./)*
,./)*
+
'(
'(
.
. '(
.
.
..
..
..
..
(c) - [EF ]α
α
..
'(
*(
*
(
*
(
α*
+
) α
(
+
+
,.
,.
, .
, .
,
.
,
.
)*
)*
,./)*
,./)*
'(
.
..
'(
. '(
.
..
..
)*
..
..
,
,
α ,+
..
'(
. '(
.
..
..
'(
.
..
..
+
*(
(
*
(
*
α*
) α
(
+
+
+
,.
.
..
.
.
./ α
+
..
.
α ,-,
+
,
,.
.
..
.
.
./ α
+
..
.
(f) - [AG]α
α +
α +
'(
.
..
(d) - [AF ]α
(e) - [EG]α
*(
*
(
*
(
β*
)*
+
)
(
+
'(
,.
,.
, .
, .
,
.
,
.
)*
)*
,./)*
,./)*
..
(b) - [AX]α
α
..
'(
.
..
'(
*(
*
(
*
(
)*
*
+
) α
(
+
'(
,.
,.
, .
, .
.
,
.
α ,-,
./ α )*
,./)*
+
+
'(
.
. '(
.
.
+
*(
(
*
(
*
α*
)*
)
(
+
+
'(
,.
,.
, .
, .
,
.
.
α ,-,
)*
,./)*
./)*
+
'(
'(
.
. '(
.
.
..
)*
,
*(
*
(
*
(
β*
+
) α
(
+
+
,.
.
,
,
.
)*
,./)*β ,+
'(
'(
.
.
.
..
..
,
,.
..
(h) - A(αUβ)
(g) - E(αUβ)
Figura 3.4: Operadores de CTL.
.
.
./ β
+
..
.
Capítulo 3. Lógicas Temporais para a Validação de Sistemas
67
Definição 3.7 (Sintaxe de LTL) Sejam Π um conjunto de letras proposicionais e P ∈ Π uma letra proposicional. A linguagem lógica de LTL é
gerada pela seguinte BNF:
Φp ::= P | (¬Φp ) | (Φp ∧Φp ) | (Φp ∨Φp ) | (Φp → Φp ) | (XΦp ) | (F Φp ) | (GΦp ) | (Φp U Φp )
Definição 3.8 (Semântica de LTL) Sejam Π um conjunto de letras proposicionais, P uma letra proposicional em Π, K = #S, So , R, L$ uma estrutura
de Kripke para Π, π um caminho da estrutura K, e α uma fórmula de LTL.
Escrevemos K |=π α para dizer que a fórmula α é satisfeita na estrutura K no
caminho π. A definição de satisfação é apresentada abaixo.
– K |=π P ⇐⇒ P ∈ L(π0 ).
PUC-Rio - Certificação Digital Nº 0310848/CB
– K |=π (¬α) ⇐⇒ NÃO K |=π α.
– K |=π (α ∧ β) ⇐⇒ K |=π α E K |=π β.
– K |=π (α ∨ β) ⇐⇒ K |=π α OU K |=π β.
– K |=π (α → β) ⇐⇒ SE K |=π α ENTÃO K |=π β.
– K |=π (Xα) ⇐⇒ K |=π1,∞ α (veja a figura 3.3.a).
– K |=π (F α) ⇐⇒ Existe um k ≥ 0 tal que K |=πk,∞ α (veja a figura 3.3.b).
– K |=π (Gα) ⇐⇒ Para todo k ≥ 0 vale que K |=πk,∞ α (veja a figura
3.3.c).
– K |=π (αUβ) ⇐⇒ Existe k ≥ 0 tal que K |=πk,∞ α e para todo 0 ≤ l < k
vale que K |=πl,∞ α (veja a figura 3.3.d).
Abaixo são apresentadas algumas fórmulas com suas relações de satisfação para o exemplo 3.2.
– K3.2 |=s,sab ,sab ,... ((¬(a ∨ b))U(a ∧ b)), que pode ser lido como ‘no caminho
s, sab , sab , . . . vale não a ou b até que vale a e b’.
– K3.2 1|=s,sa ,s,sa ,... (G a), que pode ser lido como ‘não vale no caminho
s, sa , s, sa , . . . que sempre vale a’.
– K3.2 |=s,sab ,sab ,... (F (G a)), que pode ser lido como ‘vale no caminho
s, sab , sab , . . . que no futuro sempre vale a’.
Capítulo 3. Lógicas Temporais para a Validação de Sistemas
68
Quando validamos sistemas reativos utilizando a lógica LTL, subentendemos uma quantificação universal sobre todos os caminhos de uma estrutura
de Kripke. Assim, um sistema é considerado correto em relação a um propriedade se ela é satisfeita para todos os caminhos da estrutura a partir de todos
os estados iniciais.
Na verdade, a lógica CTL* foi proposta em (EH86), como uma extensão
das duas lógicas CTL e LTL, com o intuito de estudar a relação entre estas duas
lógicas em resposta ao artigo (Lam80), que afirmava que: uma lógica de tempo
PUC-Rio - Certificação Digital Nº 0310848/CB
linear, a exemplo de LTL, expressa melhor algumas propriedades acerca de
sistemas concorrentes do que lógicas de tempo ramificado, a exemplo de CTL.
Em geral, na prova da correção de um sistema utilizamos o seguinte
princípio: ‘ao longo de qualquer caminho p será verdadeiro no futuro, ou será
sempre falso’. Este princípio é facilmente expresso em LTL como a seguinte
fórmula (F p) ∨ (G(¬p)), que é sempre válida. Por outro lado, não há uma
fórmula equivalente em CTL, por exemplo, a fórmula ([AF ]p) ∨ ([AG](¬p))
não é válida. A partir deste e outros argumentos conclui-se que, lógica com
tempo linear é melhor para expressar propriedades de sistemas concorrentes
do que lógicas com tempo ramificado. Em (EH86), esta questão é reexaminada,
e argumenta-se que este princípio pode ser facilmente expresso em CTL*, que
é uma lógica de tempo ramificado, como (A((F p) ∨ (G(¬p)))).
Há ainda um enorme debate sobre qual lógica, CTL ou LTL, é melhor
para expressar propriedades sobre sistemas concorrentes. Contudo, as propriedades usualmente utilizadas na verificação de tais sistemas podem ser expressas
em ambas as lógicas.
Diversos cálculos dedutivos corretos e completos existem para as lógicas
CTL*, CTL e LTL, tais como: uma axiomatização para CTL* em (Rey01); um
sistema de dedução natural para CTL* em (Ren04); uma axiomatização para
CTL em (Gol92); um sistema de dedução natural para CTL em (RH02); um
sistema de resolução para CTL em (BF97, Bol00); um sistema de resolução
para LTL em (Fis91); entre outros sistemas.
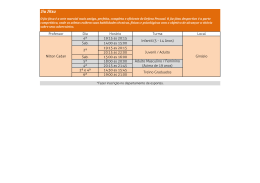
A tabela apresentada na figura 3.5 resume a complexidade para o
problema da verificação de modelos e da prova automática de teoremas
das lógicas CTL*, LTL e CTL. Uma observação sobre a complexidade da
verificação de modelos de LTL se faz necessária, é demonstrado em (LP85) que
a verificação de modelos de LTL é PSPACE-Completo, porém ela é exponencial
no tamanho da fórmula e linear no tamanho da estrutura. A partir daí, muitos
argumentam (Hol97) que, geralmente, o tamanho da fórmula a ser verificada
é pequeno em comparação ao tamanho da estrutura. Assim, na prática a
verificação de modelos de LTL é realizada de forma eficiente.
Capítulo 3. Lógicas Temporais para a Validação de Sistemas
Lógica
CTL*
LTL
CTL
Verificação de Modelos
PSPACE-Completo (LP85)
PSPACE-Completo (LP85)
Linear (CES86)
69
Satisfatibilidade
2EXP-Completo (EH86)
PSPACE-Completo (SC85)
EXP-Completo (CE81)
Figura 3.5: Complexidade de CTL*, LTL e CTL.
3.2
Verificação de Modelos em CTL
Sejam K = #S, So , R, L$ uma estrutura de Kripke, que representa um
sistema reativo com estados finitos (S finito), e α uma fórmula de CTL, que
expressa uma propriedade do sistema. O problema da verificação de modelos
é encontrar o conjunto dos estados que satisfazem a fórmula α:
{s ∈ S | K |=s α}
PUC-Rio - Certificação Digital Nº 0310848/CB
Dizemos que o sistema satisfaz a propriedade se todos estados iniciais s ∈ So
estão neste conjunto.
Um verificador de modelos é uma ferramenta que automatiza a formulação acima. O processo de validação segue os três passos abaixo:
1. Especificar em CTL quais são as propriedades que o sistema deverá ter
para que seja considerado correto. Por exemplo, podemos querer que o
sistema nunca entre em deadlock, ou ainda, que ele sempre alcance um
determinado estado.
2. O segundo passo é a construção do modelo formal do sistema, que é
definido, geralmente, em uma linguagem de alto nível (a linguagem do
verificador). O modelo deve capturar todas as propriedades essenciais
do sistema para verificar a correção do mesmo, contudo, também deverá
possuir abstrações de detalhes do sistema que não afetem a correção
das propriedades a serem verificadas. Por exemplo, em protocolos de
comunicações se está interessado em testar propriedade de quando uma
mensagem é recebida e não do conteúdo dela.
3. O terceiro e último passo é a própria execução do verificador de modelos para validar as propriedades especificadas do sistema. Neste passo,
já temos as propriedades e o modelo. Assim, aplicamos o verificador e
conseguimos garantir se o modelo do sistema possui ou não as propriedades desejadas. Caso todas as propriedades sejam verdadeiras, então o
sistema está correto. Caso não obedeça a alguma propriedade, então é
gerado um contra exemplo mostrando o porquê da não verificação da
propriedade. Desta forma, podemos detectar o erro e realizar a correção
Capítulo 3. Lógicas Temporais para a Validação de Sistemas
70
do modelo. Esse processo deve ser feito até que o sistema obedeça todas
as propriedades, realizando assim um ajuste na especificação.
A seguir iremos apresentar um algoritmo para a verificação de modelos
de CTL na seção 3.2.1, bem como o verificador de modelos Symbolic Model
Verifier (SMV) (McM93) na seção 3.2.2.
3.2.1
Algoritmo com Representação Explícita
O algoritmo descrito nesta seção utiliza uma representação explícita de
PUC-Rio - Certificação Digital Nº 0310848/CB
uma estrutura de Kripke K = #S, R, L$, através de um grafo, direcionado e
rotulado da seguinte forma. Os nós do grafo representam os estados S, os
arcos definem a relação de transição R, e os rótulos associados com cada nó
descrevem a função L : S → 2Π , onde Π é um conjunto de proposições.
No problema da verificação de modelos de CTL estamos interessados em
saber o conjunto de estados de S que satisfazem a fórmula α. O algoritmo
proposto (veja o algoritmo 1) opera rotulando cada estado s com o conjunto
label(s) de sub-fórmulas de α que são verdadeiros em s. Inicialmente, label(s) é
somente L(s), e então o algoritmo é executado uma série de passos (o número
de operadores em α). A cada passo sub-fórmulas com k − 1 operadores são
processadas. Quando uma fórmula é processada, a mesma é adicionada ao
label(s) do estado s se ela é verdadeira. Assim, K |=s α ⇐⇒ α ∈ label(s).
Lembremos que as fórmulas de CTL podem ser expressas em termos de
¬, ∨, [EX], [EG] e EU. Desta forma, é necessário tratarmos apenas estes casos
como segue.
– Para o caso (¬α1 ) (veja o algoritmo 2), rotulamos os estados que não são
rotulados por α1 . A complexidade é O(|S|).
– Para o caso (α1 → α2 ) (veja o algoritmo 3), rotulamos os estados que não
são rotulados por α1 ou são rotulados por α2 . A complexidade é O(|S|).
– Para o caso [EX]α1 (veja o algoritmo 4), rotulamos os estados que tem
algum sucessor rotulado por α1 . A complexidade é O(|S| + |R|).
– Para o caso E(α1 Uα2 ) (veja o algoritmo 5), adicionamos E(α1 Uα2 ) a to-
dos os estados rotulados com α2 , e então adicionamos E(α1 Uα2 ) retroativamente, utilizando a inversa da relação R, a todos os estados rotulados
com α1 que podem ser alcançados por um caminho. A complexidade é
O(|S| + |R|).
– Para o caso [EG]α1 (veja o algoritmo 6) temos os seguintes passos.
Capítulo 3. Lógicas Temporais para a Validação de Sistemas
71
1. Construímos K! = #S ! , R! , L! $ a partir de K = #S, R, L$, removendo
todos os estados de S que não vale α1 e restringindo R e L.
2. Utilizamos o algoritmo do Tarjan (Tar72) para particionar o grafo
#S ! , R! $ em SCCs (Strongly Connected Components), onde um SCC
é um subgrafo maximal C tal que todo nó em C é alcançável a
partir de qualquer outro nó em C através de um caminho em C.
Este algoritmo tem complexidade O(|S ! | + |R! |).
3. Adicionamos [EG]α1 aos estados que pertencem aos SCCs nãotriviais, onde um SCC é não-trivial se, e somente se, ele tem mais
de um nó ou ele contém um nó relacionado com ele mesmo.
4. Por fim, adicionamos [EG]α1 retroativamente, utilizando a inversa
PUC-Rio - Certificação Digital Nº 0310848/CB
da relação R, a todos os estados rotulados com α1 que podem ser
alcançados por um caminho.
A complexidade de toda esta computação é O(|S| + |R|). Fundamental
para a correção de tal algoritmo é o lema abaixo.
Lema 3.9 K |=s [EG]α1 ⇐⇒ s ∈ S ! e existe um caminho em K! que
leva o estado s a algum estado t em um SCC não-trivial de #S ! , R! $.
A partir dos algoritmos acima temos o seguinte teorema.
Teorema 3.10 Existe um algoritmo para determinar se uma fórmula α de
CTL é satisfeita em um estado s de K = #S, R, L$, cuja complexidade
algorítmica é O(|α| × (|S| + |R|)).
Capítulo 3. Lógicas Temporais para a Validação de Sistemas
Algoritimo 1 procedure Check(α)
while |α| ≥ 1 do
if α = (¬α1 ) then
Check(α1 )
CheckN OT (α1 )
else if α = (α1 → α2 ) then
Check(α1 )
Check(α2 )
PUC-Rio - Certificação Digital Nº 0310848/CB
CheckIM P (α1 , α2 )
else if α = [EX]α1 then
Check(α1 )
CheckEX(α1 )
else if α = [EG]α1 then
Check(α1 )
CheckEG(α1 )
else if α = E(α1 Uα2 ) then
Check(α1 )
Check(α2 )
CheckEU (α1 , α2 )
end if
end while
Algoritimo 2 procedure CheckNOT(α)
for all s ∈ S do
if α 1∈ label(s) then
label(s) := label(s) ∪ {(¬α)}
end if
end for
Algoritimo 3 procedure CheckIMP((α1 → α2 )
for all s ∈ S do
if α1 1∈ label(s) or α2 ∈ label(s) then
label(s) := label(s) ∪ {(α1 → α2 )}
end if
end for
72
Capítulo 3. Lógicas Temporais para a Validação de Sistemas
Algoritimo 4 procedure CheckEX(α1 )
T := {s | α1 ∈ label(s)}
while T 1= ∅ do
choose s ∈ T
T := T \{s}
for all t such that #t, s$ ∈ R do
if [EX]α1 1∈ label(t) then
label(t) := label(t) ∪ {[EX]α1 }
PUC-Rio - Certificação Digital Nº 0310848/CB
end if
end for
end while
Algoritimo 5 procedure CheckEU(α1 ,α2 )
T := {s | α2 ∈ label(s)}
for all s ∈ T do
label(s) := label(s) ∪ {E(α1 Uα2 )}
end for
while T 1= ∅ do
choose s ∈ T
T := T \{s}
for all t such that #t, s$ ∈ R do
if E(α1 Uα2 ) 1∈ label(t) and α1 ∈ label(t) then
label(t) := label(t) ∪ {E(α1 Uα2 )}
T := T ∪ {t}
end if
end for
end while
73
Capítulo 3. Lógicas Temporais para a Validação de Sistemas
74
Algoritimo 6 procedure CheckEG(α1 )
S ! := {s | α1 ∈ label(s)}
SCC := {C | C is a nontrivial SCC of S ! }
T := ∪C∈SCC {s | s ∈ C}
for all s ∈ T do
label(s) := label(s) ∪ {[EG]α1 }
end for
while T 1= ∅ do
PUC-Rio - Certificação Digital Nº 0310848/CB
choose s ∈ T
T := T \{s}
for all t such that t ∈ S ! and #t, s$ ∈ R do
if [EG]α1 1∈ label(t) then
label(t) := label(t) ∪ {[EG]α1 }
T := T ∪ {t}
end if
end for
end while
3.2.2
Symbolic Model Verifier (SMV)
Boa parte da pesquisa em verificação de modelos tem se concentrado
no desenvolvimento de algoritmos que usem uma representação dos sistemas
de forma mais eficiente. Uma das técnicas que obteve relativo sucesso foi a
representação através de Ordered Binary Decision Diagram (OBDD) (Bry92).
OBDDs são representações canônicas para funções booleanas, que representam
os sistemas reativos. OBDDs são freqüentemente muito mais compactas do
que representações em forma normal conjuntiva ou disjuntiva, e elas podem
ser eficientemente manipuladas.
Iremos apenas descrever o funcionamento geral de OBDDs, uma vez que
não utilizaremos tal técnica nesta tese por motivos que ficarão claros em seções
posteriores. No final desta seção, iremos apresentar a linguagem do verificador
de modelos Symbolic Model Verifier (SMV) (McM93) que foi o primeiro a
utilizar tal técnica para lógicas temporais.
Para a verificação de modelos utilizando OBDD, temos os seguintes
passos.
1. Representar uma estrutura de Kripke (um sistema) através de uma
fórmula booleana. Isto é feito, utilizando o conjunto Π de proposições,
tipicamente booleanas, para representar a estrutura de Kripke, onde
Capítulo 3. Lógicas Temporais para a Validação de Sistemas
75
as possíveis combinações dos valores associados a cada variável v em
V representam todos os possíveis estados da estrutura. A partir daí,
podemos expressar um estado através de uma fórmula booleana. No
exemplo apresentado na figura 3.2, temos duas variáveis a e b, e seus
valores podem ser verdadeiro ou falso, assim temos quatro possíveis
estados. Desta forma, podemos representar todos os possíveis estados,
mas, por outro lado, não temos como representar as relações entre
os estados utilizando tais variáveis. Para representarmos tal conceito,
utilizamos um cópia V ! das variáveis de V , onde cada variável em v ∈ V
tem uma v ! ∈ V ! correspondente no próximo estado. Por exemplo, a
estrutura da figura 3.2 é representada pela seguinte fórmula.
!
(¬A ∧ ¬B ∧ A! ∧ ¬B ! ) ∨ (A ∧ ¬B ∧ ¬A! ∧ ¬B ! ) ∨ (¬A ∧ ¬B ∧ A! ∧ B ! )
∨ (A ∧ ¬B ∧ A! ∧ B ! )
∨ (A ∧ B ∧ A! ∧ B ! )
PUC-Rio - Certificação Digital Nº 0310848/CB
2. Construir a OBDD a partir de tal fórmula booleana. Uma OBDD é uma
representação concisa de uma árvore de decisão binária que utiliza uma
ordenação nas variáveis V . A figura 3.6 abaixo representa uma árvore de
decisão binária para a fórmula (a1 ↔ b1 ) ∧ (a2 ↔ b2 ). A partir daí, uma
OBDD é construída unificando as sub-árvores que resultam no mesmo
valor de verdade. Este processo é repetido até não haver nenhuma subárvore equivalente. Por exemplo, na figura 3.7.a temos a OBDD obtida
a partir da árvore 3.6 com ordenação a1 5 b1 5 a2 5 b2 . Note que
esta é uma representação muito mais concisa do que a OBDD obtida
com ordenação a1 5 a2 5 b1 5 b2 apresentada na figura 3.7.b. De
fato, o tamanho da OBDD gerada depende fortemente da ordenação
das variáveis. Em (Bry92), é demonstrado que mesmo verificar que uma
ordenação é ótima é NP-Completo, e para alguns casos o tamanho
da OBDD é exponencial para qualquer que seja a ordenação. Diversas
heurísticas são utilizadas para tentar achar uma boa ordenação.
3. Utilizar algoritmos simbólicos para a validação de propriedades. Estes
algoritmos manipulam as OBDDs e são baseados em computação de
ponto-fixo, nos quais os operadores temporais de CTL são definidos
em função do menor ou maior ponto fixo. Veja (CGP99) para maiores
detalhes.
"
76
Capítulo 3. Lógicas Temporais para a Validação de Sistemas
)*
'(
66777
7
66
a1
66
66
)*
6
06
66
77
1
77
77
7
)*
7
'(
45
5 1
4
04
5
5
4
55
4
4
)*
)*
'(
45
5 1
4
04
5
5
4
55
4
4
)*
)*
b1
b1
'(
23
02 3 1
2
3
2
3
)*
)*
a2
'(
23
02 3 1
2
3
2
3
)*
)*
a2
'(
23
02 3 1
2
3
2
3
)*
)*
a2
'(
23
02 3 1
2
3
2
3
)*
)*
a2
'(
0 01 1
0 1
00 11
'(
0 01 1
0 1
00 11
'(
0 01 1
0 1
00 11
'(
0 01 1
0 1
00 11
'(
0 01 1
0 1
00 11
'(
0 01 1
0 1
00 11
'(
0 01 1
0 1
00 11
'(
0 01 1
0 1
00 11
1
0
0
0
0
0
1
0
b2
0
b2
1
b2
0
b2
0
b2
0
b2
0
b2
0
b2
PUC-Rio - Certificação Digital Nº 0310848/CB
Figura
3.6: Árvore de decisão binária da fórmula (a1 ↔
b1 ) ∧ (a2 ↔ b2 ).
)*
)*
a1
a1
'(
23
02 31
2
3
2
3
)*
)*
'(
'(
<;
;
<
0 ;1 <
1
;0
;
; <
)*
<
<
;
;
a2 ;
;
'(
;
9;
;
;
9
0
;
;91
9
;
;
)* 9
9)*
;
;
b2
b2
;
'(;
'(
;
;
4
(
0
1 ; 41 0
;
( 4
;
;
4
(
4
;
;; *
)
,4
.(
b1
b1
- /'
1
0
(
(a) - Ordem a1 5 b1 5 a2 5 b2 .
'(
45
5 1
04
4
5
4
5
55
44
)*
)*
'(
23
02 3 1
2
3
2
3
)*
)*
a2
'(
23
02 3 1
2
3
2
3
)*
)*
a2
1:
'( :
'(
8808 0'(
0 5 1:: '(
43 1
9
, 0
84
8
:
5
9
8
:
1 94
8
:
5
,
388
:
:
: 888
5,
4 9 ::3
888 5
:
:
44
)*
)*
9
:
8
,85
:
3
:
9
b2
b2
,
3
9
0'(
'(
, 6
9 3
770
6
( 77
9 3
,6 * 1
77
1(
9 3 666
, *
77 69
6
(
*
7
67 9
,
3
6
3
6. )7 9, * *
(
,
b1
b1
-
1
/'
b1
0
b1
(
(b) - Ordem a1 5 a2 5 b1 5 b2 .
Figura 3.7: OBDD da fórmula (a1 ↔ b1 ) ∧ (a2 ↔ b2 ).
Abaixo descrevemos as principais características da linguagem de especificação de modelos do SMV.
– Módulos – O usuário pode decompor um sistema de estados finitos em
módulos, que encapsulam uma coleção de declarações: ‘VAR’ define as
variáveis do módulo, que podem ser booleanos, conjunto enumerado de
constantes ou instâncias de outros módulos; ‘INIT’ inicializa as variáveis;
‘ASSIGN’ define as relações de transições; ‘FAIRNESS’ definem as
1
Capítulo 3. Lógicas Temporais para a Validação de Sistemas
77
fairness constraints, que são fórmulas em CTL3 ; ‘SPEC’ especificações
em CTL. Os módulos podem ser instanciados várias vezes, podem
referenciar variáveis de outros módulos e possuem parâmetros que podem
ser expressões, estados de outros módulos ou até mesmo instâncias de
módulos.
– Sincronismo e Assincronismo (Interleaved ) – módulos podem ser compostos de forma síncrona ou assíncrona. Em composição síncrona, um
passo corresponde a um passo de cada módulo. Em composição assíncrona, cada passo corresponde a um passo de um único módulo. Se a
palavra reservada ‘process’ preceder uma instância de um módulo, assincronismo é usado. Caso contrário, a composição síncrona é assumida.
Cada processo tem uma variável running que indica se o processo está
ativo ou não4 .
PUC-Rio - Certificação Digital Nº 0310848/CB
– Transições Não-Determinísticas – as transições de um estado em um
modelo podem ser determinísticas ou não-determinísticas. Transição nãodeterminística é usada para descrever modelos mais abstratos onde certos
detalhes são omitidos.
– Relações entre transições – as relações de transições de um módulo
podem ser especificadas explicitamente em termos de relações binárias
entre o atual e o próximo estado das variáveis, ou implicitamente como
um conjunto de comandos de atribuições paralelas. Os comandos de
atribuições paralelas definem o valor das variáveis no próximo estado em
termos dos valores no estado atual e são definidos através da declaração
‘NEXT’ para cada atribuição.
Abaixo apresentamos um exemplo de uma especificação no SMV.
Exemplo 3.11 Apresentamos na figura 3.8 como, seria descrito na linguagem
do SMV, um programa que utiliza uma variável semáforo ( semaforo) para
implementar exclusão mútua entre dois processo assíncronos. Será definido um
módulo usuário que terá uma variável estado que possui quatro estados: ocioso,
o processo não quer entrar na região crítica; entrando, o processo quer entrar
na região crítica; critica, o processo está utilizando a região crítica; e saindo, o
processo não irá mais usar a região crítica. O módulo ‘ main’ terá uma variável
semáforo, que será inicializada com 0, e os dois usuários. Como os processos
3
Fairness constraints são condições que são inseridas para garantir justiça aos caminhos
em CTL. Um exemplo simples é o de duas avenidas que se entroncam. Suponha que somente
passem carros de uma das avenidas. Isto claramente não seria justo. Assim, deve-se garantir
que os carros das duas avenidas possam passar no entroncamento.
4
Se a condição de running for definido nas condições de fairness de um módulo significará
que o módulo não poderá ficar indefinidamente sem ser executado.
Capítulo 3. Lógicas Temporais para a Validação de Sistemas
78
são assíncronos os usuários serão definidos com a palavra ‘ process’. A fórmula
AG!(proc1.estado = critica & proc2.estado = critica) expressa que nenhum dos
dois processos estão utilizando a região crítica ao mesmo instante. A fórmula
AG(proc1.estado = entrando − > AF (proc1.estado = critica)) significa que
PUC-Rio - Certificação Digital Nº 0310848/CB
se um processo deseja entrar na região crítica em algum instante no futuro ele
utilizará a região crítica.
MODULE main
VAR
semaforo : boolean;
proc1 : process usuario;
proc2 : process usuario;
ASSIGN
init(semaforo) :=0;
SPEC
AG !(proc1.estado=critica & proc2.estado=critica)
SPEC
AG(proc1.estado = entrando -> AF(proc1.estado = critica))
MODULE usuario
VAR
estado : {ocioso, entrando, critica, saindo};
ASSIGN
init(estado) := ocioso;
next(estado) :=
case
estado = ocioso : {ocioso,entrando};
estado = entrando & !semaforo :critica;
estado = critica : {critica, saindo};
estado = saindo : ocioso;
1 : estado;
esac;
next(semaforo) :=
case
estado = entrando : 1;
estado = saindo :0;
1 : semaforo;
esac;
FAIRNESS
running
Figura 3.8: Exclusão mútua na linguagem do SMV.