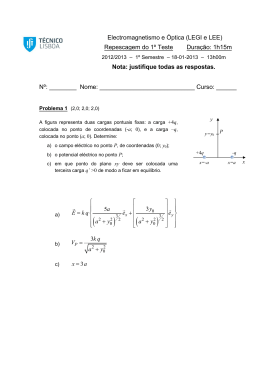
LEIC-A 2010-2011
Electromagnetismo e Óptica
Série 3
Semana 3: (27/9-1/10) 2010
Lei de Gauss (TII 22-2)
* Problema 1 (TII 22.30) : Medidas cuidadosas do campo eléctrico na superfície duma
caixa preta indicam que o fluxo eléctrico resultante que sai da superfície da caixa é 6 kN
m2/C.
a) Qual a carga resultante dentro a caixa? (R: 5.31x10 -8 C)
b) Se o fluxo resultante que sai da superfície da caixa fosse zero, poder-se-ia
concluir que não há carga no interior da caixa. Explique.
c)
** Problema 2 (TII 22.36) : Na atmosfera, a uma altitude de 250 m, o valor do campo
eléctrico é de 150 N/C dirigido para baixo e a uma altitude de 400 m o seu valor é de
170 N/C, também dirigido para baixo. Calcule a densidade volumétrica de carga da
atmosfera na região entre as altitudes de 250 e 400 m, admitindo que a densidade seja
uniforme. A curvatura da Terra pode desprezar-se? Porquê? (R: ρ= -1.17x10-12 C/m3)
Campo Eléctrico (TII 22-1)
*** Problema 3 Partindo da expressão obtida na aula teórica para o campo eléctrico
dum fio infinito uniformemente carregado com densidade linear λ0 orientado segundo o
eixo
dos
z
em
coordenadas
cartesianas/polares,
)
)
v
2kλ0  xex + ye y  2kλ0 )
E ( x, y, z ) =
=
ρ , obtenha o campo eléctrico dum plano
ρ
x 2 + y 2  x 2 + y 2 
infinito uniformemente carregado com densidade superficial, σ, admitindo que o campo
do plano pode obter-se por sobreposição dos campos duma infinidade de fios
justapostos. (R: E=2πkσ=σ/(2ε0) S.I., sentido perpendicular ao plano)
v
(N.B.: Neste contexto, ρ , é o vector posição em coordenadas polares e ρ o seu módulo. Não confundir
com o mesmo símbolo ρ utilizado para designar densidade volumétrica de carga. O significado do
símbolo será evidente pelo contexto ou então será explicitamente definido.)
v
Usando Simetria para calcular E com a Lei de Gauss (TII 22-3)
** Problema 4 (TII 22.48) : Mostre que o campo eléctrico criado por uma superfície
(casca fina) cilíndrica, infinitamente longa e uniformemente carregada, com raio a e
densidade superficial de carga,σ, é dado pelas seguintes expressões (no S.I.): E=0 para
σa
para ρ > a , sendo ρ o módulo do vector posição em
0 ≤ ρ ≤ a e Eρ =
ε 0ρ
coordenadas polares.
Problema Geral
*** Problema 5 (TII 22.69): Uma superfície (casca fina) esférica de raio R
uniformemente carregada possui uma carga total Q, positiva. Um pedaço (pequeno
elemento) de superfície é removido criando um buraco.
a) Qual o módulo, direcção e sentido do campo eléctrico no centro do buraco?
(R: E=Q/(8πε0R2))
b) O elemento removido é colocado novamente onde estava. (Figura 22-44b).
Utilizando o resultado da alínea anterior, determine a força eléctrica exercida
sobre o pequeno elemento que foi retirado. (R: F=Q2a2/(32πε0R4))
c) Usando a magnitude da força, calcule a pressão electrostática que tende a
expandir a superfície esférica. (R: P=Q2/(32π2ε0R4))
Nota: As referências ao livro do Tipler vêm da 6ª Edição, Física Para Cientistas e
Engenheiros, Vol. II (Electricidade e Magnetismo, Óptica) de Paul Tipler e Gene
Mosca, LTC Editora, 2009. A seguinte forma abreviada é utilizada: TII 21-1 significa
Tipler, Vol. II, Capítulo 21, Secção 1 e TII 21.34 significa Tipler, Vol. II, Capítulo 21,
Problema 34.