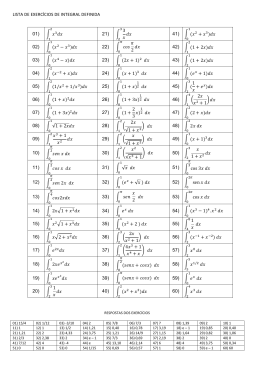
LISTA DE EXERCÍCIOS – DERIVADA
2010-2
I. DERIVADAS POR DEFINIÇÃO, EQUAÇÃO DA RETA TANGENTE
1) Determine a equação da reta tangente à função f (x) no ponto indicado:
1
x
a) f ( x)  x 2
x2
b) f ( x) 
c) f ( x) 
x9
d) f ( x)  x 2  x
x
x2
x 1
2) Calcule f ' ( x) , pela definição.
a) f ( x)  x 2  x
x 1
b) f ( x) 
c) f ( x)  5x  3
x  3
1
x
1
f) f ( x)  2
x
h) f ( x)  x 3
e) f ( x) 
d) f ( x) 
x3
x
g) f ( x)  3x  1
x
x 1
x3
k) f ( x) 
2x  4
i) f ( x) 
x4
x
x 1
x2
j) f ( x)  3x  4
l) f ( x) 
2x  5
Soluções:
1-
a) y  4 x  4
2-
a) 3
h) 3x 2
b)
b) y  
1
4
i)
1
x 1
4
d)  1
c) 5
1
( x  1) 2
c) x  6 y  9  0
j)
3
2 3x  4
e)
1
2 3
k)
10
(2 x  4) 2
d) y  x  1
f) 
1
4
g) 3
l)
1
2x  5
Página 1
LISTA DE EXERCÍCIOS – DERIVADA
2010-2
II. REGRAS DE DERIVAÇÃO
1) Determine a derivada da função indicada:
1
2
1
1
1) f ( x)   x 4  x 3  x 2 
2
3
2
4
f ' ( x)  2 x 3  2 x 2  x
2) f ( x)  x 2  x
f ' ( x)  2 x 
1
3) f ( x)  x cos x
2 x
f ' ( x)  3 x cos x  x 3 senx
4) f ( x)  x 3 (2 x 2  3 x)
f ' ( x)  10 x 4  12 x 3
3
5) f ( x) 
2
2x  5
4x
f ' ( x)  
x
5
4x2
x
2
6) f ( x)   
5
7) f ( x)  23 x 1
2 2
f ' ( x)    ln
5 5
f ' ( x)  23 x 1.3 ln 2
8) f ( x)  3x
f ' ( x)  3x ln 3
9) f ( x)  sen( x 2 )
f ' ( x)  2 x. cos( x 2 )
1
10) f ( x)  cos 
 x
2
11) f ( x)  ( x  5 x  2)7
1
1
sen 
2
x
 x
2
f ' ( x)  7( x  5 x  2)6 (2 x  5)
 3x  2 
12) f ( x)  

 2x  1 
1
13) f ( x)  (2 x 5  6 x  3 )5
3
1
 3x  2 
f ' ( x)  5
.
2
 2 x  1  (2 x  1)
10
f ' ( x)  (2 x 5  6 x  3 ) 4 .(5 x 4  9 x  4 )
3
5
6x
y'  6
x 1
3x 2
y'
6
3
5( x  1) 5
5
14) y  ln( x 6  1)
15) y 
1
5
x3  1
f ' ( x) 
4
16) y  cos( x 3  4)
y '   sen( x 3  4)(3 x 2 )
17) y  ( x 3  6)5
y '  15 x 2 ( x 3  6) 4
Página 2
LISTA DE EXERCÍCIOS – DERIVADA
2010-2
18) y  3x 2  5
y'  6 x
19) y  23 x
y' 
20) y 
4 5

x x2
x
21) y  2
x 1
2
3
3 x2
1  x2
y'  2
( x  1) 2
22) y 
3x 2  3
5x  3
y' 
23) y 
x
x 1
y' 
24) y 
cos x
x2  1
y'  
25) y 
3
senx  cos x
y' 
26) y  cos x  ( x 2  1)senx
27) y 
x 1
x.senx
4 10

x 2 x3
y'  
15 x 2  18 x  15
(5 x  3) 2
1 x
2 x ( x  1) 2
( x 2  1).senx  2 x cos x
( x 2  1) 2
 3(cos x  senx)
( senx  cos x) 2
y'  senx(2 x  1)  cos x( x 2  1)
y'  
x( x  1). cos x  senx
x 2 .sen2 x
28) y  sen4 x
y'  4. cos 4 x
29) y  e3 x
y'  3e3 x
30) y  sen t 3
y'  3t 2 cos t 3
31) y  ln( 2t  1)
y' 
32) y  (senx  cos x)3
y'  3(senx  cos x)2 (cos x  senx)
33) y  3x  1
y' 
34) y 
3
x 1
x 1
2
2t  1
3
2 3x  1
2
y' 
.3
3( x  1) 2
 x 1


 x 1 
2t  3
t  3t  9
35) y  ln(t 2  3t  9)
y' 
36) y  sen(cos x)
y'  senx. cos(cos x)
2
Página 3
2
LISTA DE EXERCÍCIOS – DERIVADA
2010-2
37) y  (t 2  3)4
y'  8t (t 2  3)3
38) y  cos( x 2  3)
y'  2 xsen( x 2  3)
39) y  x  e x
y' 
40) y  sec 3x
y'  3sec 3xtg 3x
41) y  cos 8x
y'  8sen8x
42) y  esent
y'  esent . cos t
43) y  e5 x
y'  5e5 x
44) y  cos e x
y'  e x .sene x
1 ex
2 x  ex
Página 4