CÁLCULO 1 – Teoria 0: Revisão Gráfico de Funções elementares
Núcleo de Engenharias e Ciência da Computação
Professora: Walnice Brandão Machado
FUNÇÕES POLINOMIAIS
Função polinomial de 1º grau
O gráfico de uma função polinomial do 1º grau, y = ax + b, com a
aos eixos Ox e Oy.
0, é uma reta oblíqua
Exemplo: y = 3x – 1
Função Quadrática (polinomial de 2º grau)
2
O gráfico de uma função polinomial do 2º grau, y = ax + bx + c, com a
chamada parábola.
0, é uma curva
Construção da Parábola:
É possível construir o gráfico de uma função do 2º grau sem montar a tabela de pares (x, y),
mas seguindo apenas o roteiro de observação seguinte:
1.
O valor do coeficiente a define a concavidade da parábola;
2.
Os zeros definem os pontos em que a parábola intercepta o eixo dos x (quando isso
ocorrer);
3.
O vértice V
4.
A reta que passa por V e é paralela ao eixo dos y é o eixo de simetria da parábola;
5.
Para x = 0 , temos y = a · 0 + b · 0 + c = c; então (0, c) é o ponto em que a parábola
corta o eixo dos y.
Observação: Quando
indica o ponto de mínimo (se a > 0), ou máximo (se a< 0);
2
é negativo, não há raiz real, logo, a parábola não intercepta o eixo
das abscissas, ficando inteiramente acima dele (no caso de a > 0 ) ou inteiramente abaixo
dele, quando a < 0.
2
Exemplo: y = x + x:
FUNÇÃO EXPONENCIAL
Chamamos de funções exponenciais aquelas nas quais temos a variável aparecendo
em expoente.
+
x
+
A função f:IRIR definida por f(x)=a , com a IR e a 1, é chamada função
exponencial de base a.
Gráfico da função exponencial
Temos 2 casos a considerar:
 quando a>1;
 quando 0<a<1.
a>1
0<a<1
f(x) é crescente e Im=IR +
f(x) é decrescente e Im=IR+
Para quaisquer x1 e x2 do domínio: Para quaisquer x 1 e x2 do domínio:
x2>x1  y2>y1 (as desigualdades x2>x1  y2<y1 (as desigualdades
têm mesmo sentido)
têm sentidos diferentes)
Observe que na função exponencial:
a) o gráfico nunca intercepta o eixo horizontal, ou seja, a função não tem raízes;
b) o gráfico corta o eixo vertical no ponto (0,1);
c) os valores de y são sempre positivos (potência de base positiva é positiva), portanto o
+
conjunto imagem é Im=IR .
Função exponencial (de base e)
A função exponencial (de base ) é a função real de variável real que a cada x
faz
x
corresponder
(recorde que denota o número de Neper). As propriedades e a “aparência do
gráfico” seguem às mesmas condições de uma função exponencial de base maior que 1.
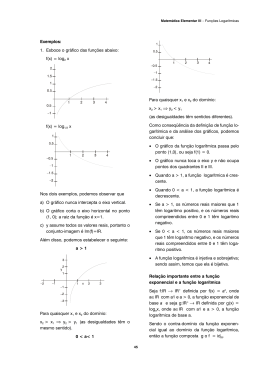
FUNÇÃO LOGARÍTMICA
+
A função f:IR IR definida por f(x)=log ax, com a 1 e a > 0, é chamada função
logarítmica de base a.
GRÁFICO CARTESIANO DA FUNÇÃO LOGARÍTMICA
Temos 2 casos a considerar:
 quando a>1;
 quando 0<a<1.
a>1
0<a<1
f(x) é crescente e Im=IR
f(x) é decrescente e Im=IR
Para quaisquer x1 e x2 do domínio: Para quaisquer x1 e x2 do domínio:
x2>x1  y2>y1 (as desigualdades x2>x1  y2<y1 (as desigualdades
têm mesmo sentido)
têm sentidos diferentes)
Observe que na função logarítmica:
d) o gráfico nunca intercepta o eixo vertical;
e) o gráfico corta o eixo horizontal no ponto (1,0), ou seja, a raiz da função é x=1;
f) y assume todos os valores reais, portanto o conjunto imagem é Im=IR.
Função logarítmica (de base e)
f ( x ) ln x
A função logarítmica (de base ) é a função real de variável real que a cada x
faz
corresponder loge x (recorde que denota o número de Neper) que normalmente é
representado por f ( x ) ln x . É também conhecida como logaritmo neperiano. As
propriedades e a “aparência do gráfico” seguem às mesmas condições de uma função
logarítmica de base maior que 1.
FUNÇÕES TRIGONOMÉTRICAS
Função y = sen (x)
Função y = cos (x)
Para detalhes sobre as funções trigonométricas consulte www.somatematica.com.br
FUNÇÃO RACIONAL f(x) = 1/x
Seja a função real de variável real f: \{0}→
definida por
1
f ( x)  .
x
Recorde que esta função tem as seguintes propriedades:

 Domínio:
(todos os números reais, exceto o zero);

 Zeros e Sinal:
o não tem zeros
o positiva em e negativa em

 Extremos e Monotonia:
o não tem nem mínimos nem máximos
o é sempre decrescente

 Contradomínio:
(todos os números reais, exceto o zero);

 A função é ímpar

 A função é contínua no seu domínio

 Gráfico
o hipérbole equilátera
IR 

concavidade voltada para baixo em IR
o
concavidade voltada para cima em
o
o
o
assíntota horizontal: reta de equação y =0 (eixo dos xx)
assíntota vertical: reta de equação x =0 (eixo dos yy)
Na figura abaixo encontra-se representado o gráfico da função f e respectivas assíntotas (o
eixo dos xx e o eixo dos yy).
Fonte: http://modulos.math.ist.utl.pt/html/PropFuncp2.shtml - Acesso em 01/08/2010.
FUNÇÃO DEFINIDA POR PARTES
Denominamos função definida por partes toda função definida com a aplicação de fórmulas
diferentes a diferentes partes do domínio.
Exemplo 1:

0, se t 0
H (t ) 

1, se t 0

Exemplo 2: