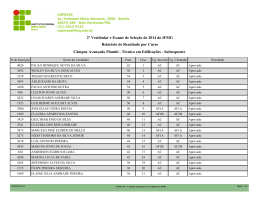
FUNÇÃO IDENTIDADE ............................................................... 2
FUNÇÃO LINEAR ........................................................................ 2
FUNÇÃO AFIM............................................................................. 5
GRÁFICO DA FUNÇÃO DO 1º GRAU ......................................... 5
IMAGEM ..................................................................................... 14
COEFICIENTES DA FUNÇÃO AFIM ......................................... 14
ZERO DA FUNÇÃO AFIM .......................................................... 18
FUNÇÕES CRESCENTES OU DECRESCENTES.................... 19
SINAL DE UMA FUNÇÃO .......................................................... 24
SINAL DA FUNÇÃO AFIM ......................................................... 25
INEQUAÇÕES ........................................................................... 29
SISTEMA DE INEQUAÇÕES ..................................................... 33
INEQUAÇÕES SIMULTÂNEAS ................................................. 34
INEQUAÇÕES-PRODUTO ........................................................ 39
INEQUAÇÃO-QUOCIENTE ....................................................... 48
RESPOSTAS ............................................................................. 61
REFERÊNCIA BIBLIOGRÁFICA ................................................ 68
No final das séries de exercícios podem aparecer
sugestões de atividades complementares. Estas
sugestões referem-se a exercícios do livro
“Matemática” de Manoel Paiva fornecido pelo
FNDE e adotado pelo IFMG – Campus Ouro Preto
durante o triênio 2015-2017.
Todos os exercícios sugeridos nesta apostila se
referem ao volume 1.
MATEMÁTICA I
1
FUNÇÃO DO 1º GRAU
FUNÇÃO IDENTIDADE
FUNÇÃO LINEAR
Uma função f de
em
recebe
o nome de FUNÇÃO IDENTIDADE
quando associa a cada elemento x 
o próprio x, isto é:
f:
Uma função f de
em
recebe
o nome de FUNÇÃO LINEAR quando
associa
a
cada
elemento
x
o elemento ax 
onde a  0 é
o número real dado, isto é:

f(x) = x
f:

f(x) = ax com a  0 (1)
Desta forma, todos os pares
ordenados que pertencem à função
identidade são do tipo (a; a) e o gráfico
que a representa contém as bissetrizes
do 1º e 3º quadrantes.
É possível demonstrar que o
gráfico da função linear é uma reta que
passa pela origem, mas veremos esta
demonstração mais a frente, num caso
mais geral.
A imagem da função identidade é
Im =
e isto pode ser percebido
facilmente, veja:
f ( x)  a  x  y  a  x
y
y  ax  x 
a
A imagem da função identidade é
Im =
.
1
Observe que se a = 0, teremos uma função
constante y = 0 como vimos na apostila anterior.
CÁSSIO VIDIGAL
2
IFMG – CAMPUS OURO PRETO
𝑦
, a  0, tal que:
assim, 𝑥 = 𝑎 ∈
f (x)  a  x
y
a
f (x)  y
f (x)  a 
Ex.: 1
Vamos construir o gráfico da função
y = 2x.
Resolução: como já sabemos que o
gráfico da função linear é uma reta e que
dois pontos distintos determinam uma
reta, basta que encontremos dois pontos
para construir o gráfico.
Por outro lado o gráfico da função linear
passa sempre pela origem assim, já
temos o ponto (0; 0) bastando encontrar
apenas mais um ponto.
Vamos, então, atribuir um valor não nulo
a x e calcular o correspondente y = 2x.
Ex.: 2
Construir o gráfico da função y = -2x.
Resolução:
Analogamente, temos:
x
1
-2 • x
-2 •1
Y
-2
Agora, P(0; 0) e Q(1; -2).
x
1
2•x
2 •1
y
2
Agora devemos localizar, num sistema
cartesiano, os pontos P(0; 0) e Q(1; 2) e
traçar a reta PQ que será o gráfico
procurado.
Note que Im(f) =
.
Veja o gráfico na coluna a seguir.
MATEMÁTICA I
3
FUNÇÃO DO 1º GRAU
2) Construir, num mesmo sistema
cartesiano, os gráficos das funções
f:

a seguir.
1) Construa, num mesmo sistema
cartesiano, os 4 gráfico de funções
constantes a seguir.
a) y = x
a) y = 2
b) y =
b) y = 2x
2
c) y = 3x
c) y = -3
d) y 
d) y = 0
CÁSSIO VIDIGAL
4
x
2
IFMG – CAMPUS OURO PRETO
FUNÇÃO AFIM
3) Construir, num mesmo sistema
cartesiano, os gráficos das funções
f:

a seguir.
Uma função f de
em
recebe
o nome de FUNÇÃO AFIM quando
associa
a
cada
elemento
x
o elemento ax + b 
onde a 
0, isto é: f:

f(x) = ax + b com
a0
a) y = -x
b) y = -2x
c) y = -3x
d) y  
x
2
1.: y = 2x + 4 onde a = 2 e b = 4
2.: y = -3x + 5 onde a = -3 e b = 5
3.: y = x – 1 onde a = 1 e b = -1
4.: y = 3x onde a = 3 e b = 0
Observe este último exemplo.
Note que, quando b = 0, a função
y = ax + b assume a forma da função
linear e, assim, podemos dizer que a
função linear é um caso particular de uma
função afim.
GRÁFICO DA FUNÇÃO
DO 1º GRAU
O gráfico da função do primeiro
grau é uma reta e isto pode ser facilmente
demonstrado.
Demonstração:
MATEMÁTICA I
5
FUNÇÃO DO 1º GRAU
De 4 ,
y 2  y1  ax 2  x1 
a
De 5 ,
y 3  y 2  ax 3  x 2 
a
Sejam A, B e C três pontos
quaisquer distintos pertencentes ao
gráfico cartesiano da função y = ax + b
com a  0 e (x1; y1), (x2; y2) e (x3, y3),
respectivamente,
as
coordenadas
cartesianas destes pontos.
Assim, a 
y 2  y1 y 3  y 2

x 2  x1 x 3  x 2
Sabendo, agora, que o gráfico da
função afim é uma reta e que para
determinar uma reta precisamos apenas
de dois pontos, vamos usar deste recurso
para construir tais gráficos. Veja nos
exemplos a seguir.
1
2
x 2 ; y 2   f  y 2  ax2  b
x 3 ; y 3   f  y 3  ax3  b
y3  y2
x3  x2
Logo os triângulos ABD e BCE
são semelhantes e assim, os ângulos  e
 são iguais e, consequentemente A, B e
C estão alinhados. Daí está provado que
o gráfico da função afim é uma reta.
Para provar que os pontos A, B e
C pertencem a uma mesma reta, vamos
mostrar, em princípio, que os triângulos
ABD e BCE são semelhantes.
Note que
:
x1; y1   f  y1  ax1  b
y 2  y1
x 2  x1
3
Fazendo 3  2 , temos:
y 3  ax3  b
y 2  ax 2  b
y 3  y 2  ax 3  x 2 
4
Ex. 1: Construir o gráfico da função
y = 2x + 1.
Fazendo 2  1 , temos:
y 2  ax 2  b
y1  ax1  b
y 2  y1  ax 2  x1 
CÁSSIO VIDIGAL
Resolução;
Sabendo que este gráfico é uma
reta, vamos encontrar dois de seus
pontos, localiza-los no plano cartesiano
e, em seguida traçar a reta.
5
6
IFMG – CAMPUS OURO PRETO
x
2x+1
y
0
2•0+1
1
1
2•1+1
3
Assim, o gráfico da função, então,
é a reta que passa pelos pontos
(0; 3) e (2; 1).
O gráfico da função, então, é uma
reta que passa pelos pontos (0; 1) e
(1; 3).
D(f) =
e Im(f) =
É facilmente perceptível, pelo
gráfico, que tanto o domínio quanto a
imagem desta função são formados por
todos os números reais, assim:
D(f) =
Im(f) =
Ex. 2: Construir o gráfico da função
y = -x + 3
Resolução:
De modo análogo, temos:
x
-x + 3
y
0
-0 + 3
3
2
-2 + 3
1
MATEMÁTICA I
4) Construa nos planos cartesianos a
seguir, o gráfico da cada uma das 8
funções apresentadas.
(Dica: em cada situação siga os
exemplos fazendo, inclusive, a tabela
afim de que a construção fique
organizada)
7
FUNÇÃO DO 1º GRAU
a) y = 2x – 1
x
c) y = 3x+2
y
x
b) y = x+2
x
d) y 
y
2x  3
2
x
CÁSSIO VIDIGAL
8
y
y
IFMG – CAMPUS OURO PRETO
e) y = –3x – 4
x
g) y = –2x + 3
y
x
f) y = –x – 1
x
h) y 
y
4  3x
2
x
MATEMÁTICA I
9
y
y
FUNÇÃO DO 1º GRAU
5)
Resolver
analiticamente
e
graficamente o sistema de equações do
1º grau:
 x  y  3

2x  3 y  4
(A resolução desta questão pode ser
vista na secção de Respostas)
CÁSSIO VIDIGAL
6) Resolva analiticamente e graficamente
os sistemas de equações do 1º grau:
x  y  5
a) 
x  y  1
10
IFMG – CAMPUS OURO PRETO
x  2y  2
c) 
2x  4y  4
3x  2y  14
b) 
2x  3y  8
MATEMÁTICA I
11
FUNÇÃO DO 1º GRAU
7) Resolva os sistemas:
1
3
 1
x  y  x  y  4

a) 
 1  1 1
 x  y x  y
4
Sugestão: faça
CÁSSIO VIDIGAL
1
a
xy
2
5
 3
 x  y  1  2x  y  3  12

b) 
3
 2

1
 x  y  1 2x  y  3
e
1
b
xy
12
IFMG – CAMPUS OURO PRETO
c) (3; -2) e (2; -3)
8) Obter a equação da reta que passa
pelos pontos:
a) (1; 2) e (3; -2).
(A resolução deste item a) pode ser vista
na secção de Respostas)
d) (1; -1) e (-1; 2)
b) (2; 3) e (3; 5)
______________________
ATIVIDADES COMPLEMENTARES
Pág. 153 e 154– Exercícios 02 a 04
______________________
MATEMÁTICA I
13
FUNÇÃO DO 1º GRAU
IMAGEM
O conjunto imagem de uma função
afim f:

definida por
f(x) = ax + b com a  0 é
.
De fato, qualquer que seja y 
,
y b
existe

tal que
x
a
y b
 y b
f x   f 
b  y.
  a
a
 a 
COEFICIENTES DA FUNÇÃO
AFIM
Observe que a variação do coeficiente a
faz variar a declividade da reta que
representa o gráfico da função.
O coeficiente a da função
f(x) = ax + b é denominado coeficiente
angular ou declividade da reta
representada no plano cartesiano.
Ex.2: Agora você pode observar
construções de funções que possuem o
mesmo coeficiente angular variando,
apenas, o coeficiente linear.
O coeficiente b da função
y = ax + b é denominado coeficiente
linear.
Os coeficientes a e b tem
influência sensível no gráfico da função
afim.
Veja os exemplos a seguir onde
são mostradas variações independentes
em cada coeficiente.
Ex.1: Veja a construção, num mesmo
plano cartesiano, de gráficos de 6
funções. Note que em todos os casos, o
coeficiente b não muda. A única variação
é no coeficiente a.
CÁSSIO VIDIGAL
Vejam neste caso, que a variação do
coeficiente b faz variar o ponto em que a
reta do gráfico da função toca o eixo OY.
14
IFMG – CAMPUS OURO PRETO
11) Obter a equação da reta que passa
pelo ponto (-3; 1) e tem coeficiente
1
angular igual a  .
2
9) Obter a equação da reta que passa
pelo ponto (1; 3) e tem coeficiente
angular igual a 2.
(A resolução desta questão pode ser
vista na secção de Respostas)
12) Obter a equação da reta que passa
pelo ponto (-2; 1) e tem coeficiente
angular igual a 4.
10) Obter a equação da reta que passa
pelo ponto (-2; 4) e tem coeficiente
angular igual a -3.
MATEMÁTICA I
15
FUNÇÃO DO 1º GRAU
13) Obter a equação da reta que tem
coeficiente angular igual a -3 e passa
pelo ponto (-3; -2)
14) Dados os gráficos das funções de
em
, obter a lei de correspondência
dessas funções. Para tal considere cada
quadradinho como referência de uma
unidade.
a)
CÁSSIO VIDIGAL
16
IFMG – CAMPUS OURO PRETO
b)
MATEMÁTICA I
c)
17
FUNÇÃO DO 1º GRAU
ZERO DA FUNÇÃO AFIM
d)
Zero ou raiz de uma função é todo
número x cuja imagem é nula, isto é, f(x)
= 0.
x é zero de y = f(x)  f(x) = 0
Assim, para determinar o zero de
uma função afim, basta resolver a
equação do 1º grau
ax + b = 0
que apresenta uma única solução
x
b
.
a
Ex.1:
Qual o zero da função f(x) = 2x – 1?
2x  1  0
2x  1
1
x
2
Logo, a raiz da função é
1
.
2
Ex. 2:
Podemos interpretar o zero da
função afim como sendo a abscissa do
ponto onde o gráfico corta o eixo OX.
Note o gráfico da função
f(x) = 2x – 1, podemos perceber que o
gráfico intercepta o eixo das abscissas
1
1 
em x  , isto é, no ponto  ; 0  .
2
2 
CÁSSIO VIDIGAL
18
IFMG – CAMPUS OURO PRETO
Veja, agora, no gráfico, a
caracterização de uma função crescente.
FUNÇÕES CRESCENTES OU
DECRESCENTES
Uma função f: A  B definida por
y = f(x) é DECRESCENTE no conjunto A1
 A se, para dois valores quaisquer x1 e
x2 pertencentes a A1, com x1 < x2,
tivermos f(x1) > f(x2).
Uma função f: A  B definida por
y = f(x) é CRESCENTE no conjunto
A1  A se, para dois valores quaisquer x1
e x2 pertencentes a A1, com x1 < x2,
tivermos f(x1) < f(x2).
Em termos técnicos, f é crescente
quando:
Em termos técnicos, f é crescente
quando:
( x1, x2) (x1 < x2  f(x1) > f(x2))
( x1, x2) (x1 < x2  f(x1) < f(x2))
Esta expressão acima também pode ser
escrita desta forma:
( x1, x2) (x1  x2 
Esta expressão acima também
pode ser escrita desta forma:
f x1   f x 2 
 0)
x1  x 2
( x1, x2) (x1  x2 
Em termos não técnicos, podemos
dizer que uma função é crescente num
certo intervalo quando se, ao aumentar o
x, o valor de y também aumenta.
MATEMÁTICA I
f x 1   f x 2 
 0)
x1  x 2
Em termos não técnicos, podemos
dizer que uma função é decrescente num
certo intervalo quando se, ao aumentar o
x, o valor de y diminui.
19
FUNÇÃO DO 1º GRAU
Veja, agora,
caracterização
de
decrescente.
no gráfico, a
uma
função
Veja o exemplo abaixo. A função é
decrescente em - e crescente em +.
Ex.1: A função f(x) = 2x – 1 é crescente
pois tomados dois valores de x distintos
x1 e x2 com x1 < x2, temos:
x1  x 2  2x1  1  2x 2  1
15) Com base nos gráficos a seguir, de
funções de domínio e contradomínio
reais, especificar onde a função é
crescente e onde a função é decrescente.
Ex.2: A função f(x) = -3x + 2 é
decrescente pois tomados dois valores
de x distintos x1 e x2 com x1 < x2, temos:
x1  x 2  3x1  2  3x 2  2
a)
Notemos que uma função y = f(x) pode
assumir
comportamentos
variados
(crescente ou decrescente) em todo o
seu domínio.
É bastante comum que, inclusive,
que a função seja crescente em alguns
intervalos e decrescentes em outros.
CÁSSIO VIDIGAL
20
IFMG – CAMPUS OURO PRETO
b)
O estudo do comportamento
quanto a crescimento ou decrescimento
de uma função afim é feito em relação
ao coeficiente angular.
A função afim é crescente se, e
somente se, o coeficiente angular for
positivo.
Dada a função f(x) = ax + b,
Se a > 0 então f é crescente.
DEMONSTRAÇÃO
f x   ax  b é crescente

f x1   f x 2 
 0 ( x1  x 2 )
x1  x 2

ax1  b  ax2  b  0
x1  x 2
c)

ax1  b  ax 2  b
0
x1  x 2

ax1  x 2 
0
x1  x 2

a0
Assim, podemos observar que
f(x) = ax + b é crescente  a > 0
MATEMÁTICA I
21
FUNÇÃO DO 1º GRAU
17) Especificar se cada uma das funções
abaixo é crescente ou decrescente.
a) y = 2x + 8
16) Demonstre que f(x) = ax + b se, e
somente se, a < 0.
b) y = 3x – 9
c) y = -4x + 6
d) y = -2x – 6
e) y 
x
1
5
f) y  2x 
CÁSSIO VIDIGAL
22
1
2
IFMG – CAMPUS OURO PRETO
g) y 
1 x
2
h) y  1 
19) Estudar, segundo os valores do
parâmetro k, a variação (crescente,
decrescente ou constante) das funções
abaixo.
a) y = (k – 1)x + 2
(A resolução deste item a) pode ser vista
na secção de Respostas)
3x
2
18) Para quais valores de k a função
f(x) = (k + 5)x – 7 é crescente?
MATEMÁTICA I
b) y = (k + 5)x – 7
23
FUNÇÃO DO 1º GRAU
c) y = (4 – k)x + 2
Estudar o sinal da função y = f(x) cujo
gráfico está representado na figura a
seguir.
d) y = k(x + 3) – 5
Como foi dito, não importa a
posição do eixo das ordenadas, então
vamos retira-lo e preparar um aspecto
prático.
SINAL DE UMA FUNÇÃO
Seja a função f: A  B definida por
y = f(x). Estudar o sinal da função é
determinar para que valores de x temos y
maior, menor ou igual a zero.
Conclusão:
f(x) = 0 para
x = -3 ou x = 1 ou x = 4 ou x = 8
Graficamente, isto pode ser feito
observando os intervalos em que o
gráfico está acima ou abaixo do eixo x.
f(x) > 0 para
-3 < x < 1 ou 1 < x < 4 ou x > 8
Note que o que realmente
interessa é o comportamento do gráfico
em relação ao eixo OX não importando a
posição do eixo OY.
CÁSSIO VIDIGAL
f(x) < 0 para
x < -3 ou 4 < x < 8
24
IFMG – CAMPUS OURO PRETO
SINAL DA FUNÇÃO AFIM
Como vimos, estudar o sinal De
uma função y = f(x) significa estabelecer,
para cada valor de x  D(f), qual das
sentenças é verdadeira:
20) Estudar o sinal das funções cujos
gráficos estão representados a seguir.
a)
y>0
y=0
y<0
Para a função afim y = ax + b,
temos com dois casos a considerar:
1º caso: a > 0
Neste caso a função é crescente. Como
b
 b
para x   temos y  f     0 , vem:
a
 a
b)
x
b
 b
 f x   f     f x   0
a
 a
x
b
 b
 f x   f     f x   0
a
 a
Considerando os valores de x
sobre um eixo, o sinal da função da
função y = ax + b com a > 0, é:
Entende-se, com esta notação,
b
que para valores de x à direita de  , a
a
função retorna um valor positivo ( + ) e
b
para valores à esquerda de  , a função
a
retorna valores negativos ( - ).
c)
Um outro processo de analisarmos
a variação do sinal da função afim é
construir o gráfico cartesiano.
MATEMÁTICA I
25
FUNÇÃO DO 1º GRAU
Já vimos que o gráfico cartesiano
da função f(x) = ax + b é uma reta e se o
coeficiente angular a é positivo, a função
é crescente.
Entende-se, com esta notação,
b
que para valores de x à direita de  , a
a
função retorna um valor negativo ( - ) e
b
para valores à esquerda de  , a função
a
retorna valores positivo ( + ).
Construindo
o
gráfico
de
f(x) = ax + b com a > 0 e lembrando o que
está sendo dito na página 24, que a
posição do eixo y não importa, temos:
Também podemos analisar com a
construção do gráfico lembrando que
para a > 0, a função é decrescente.
2º caso: a < 0
Podemos fazer um resumo do
estudo do sinal da função afim como está
no quadro em destaque na coluna ao
lado. Observe:
Neste caso a função é de crescente.
b
Também
para
temos
x
a
 b
y  f     0 , vem:
 a
b
 b
x    f x   f     f x   0
a
 a
b
 b
x    f x   f     f x   0
a
 a
b

f x   0 se x   a

b

Quando a > 0, f x   0 se x  
a

b

f x   0 se x   a

Considerando os valores de x
sobre um eixo, o sinal da função da
função y = ax + b com a < 0, é:
CÁSSIO VIDIGAL
26
IFMG – CAMPUS OURO PRETO
f 3  2  3  1  f 3  7
b



f
x

0
se
x



a

b

Quando a < 0, f x   0 se x  
a

b

f x   0 se x   a

f  5  2   5  1  f  5  9
Ex.2: Estudar
f(x) = -2x + 3.
o
sinal
da
função
f x   0  2x  3  0  2x  3  x 
3
2
Como a < 0 (a = -2), temos que a
função f é decrescente, assim:
Ex.1: Estudar
f(x) = 2x + 1.
o
sinal
da
função
f x   0  2x  1  0  2x  1  x  

x 


x 


x 

1
2
Como a > 0 (a = 2), temos que f é
crescente, assim:
3
y 0
2
3
y 0
2
3
y 0
2
Mais uma vez vamos verificar a
resposta com um valor maior que a raiz
( 5 ) e outro menor que a raiz ( 1 ).
1

x   2  y  0

1

x    y  0
2

1

x   2  y  0

f 1  2  1 3  f 1  1
f 5  2  5  3  f 1  7
Note que, de fato, quando
procuramos, pela função acima, a
imagem de um número qualquer maior
1
que  , encontraremos um valor
2
1
positivo. A imagem de 
é zero e a
2
imagem de qualquer valor menor que
1
 é um número negativo
2
Só para exemplificar, vamos
1
encontrar os valores de f(3) (3 >  ) e
2
1
de f(-5) (-5 <  )
2
MATEMÁTICA I
27
FUNÇÃO DO 1º GRAU
d) f(x) = 5 + x
21) Estudar os sinais das seguintes
funções definidas em
:
a) f(x) = 2x + 3
e) f x   3 
x
2
b) f(x) = -3x + 2
f) f x  
x 3

3 2
c) f(x) = 4 – x
CÁSSIO VIDIGAL
28
IFMG – CAMPUS OURO PRETO
g) f x   2x 
4
3
INEQUAÇÕES
O último exercício apresentado
(22) é um exemplo de inequação. Vamos
agora resolver outras inequações.
Ex.: Seja f:

a função definida por
f(x) = 4x – 5. Determine os valores do
domínio para os quais a função produz
imagem maior que 3.
Note que este exemplo é bem parecido
com o último exercício. Para encontrar a
solução, basta resolver a inequação
h) f(x) = -x
4x – 5 > 3
4x > 8
x>2
Logo a solução é S = {x 
| x > 2}
Ex.2:
Considerando
as
funções
f(x) = 4x – 1 e g(x) = -x + 3, determine os
valores de x para os quais temos
f(x)  g(x).
Vamos resolver a inequação:
______________________
ATIVIDADES COMPLEMENTARES
Pág. 163 – Exercícios 18 a 20
______________________
4x  1  x  3
4x  x  3  1
5x  4
22) Seja f:

a função definida por
f(x) = 4x – 5. Determine os valores do
domínio para os quais a função produz
imagem maior que 0 (zero).
x
4
5
4

Solução: S  x   | x  
5

Esta solução pode ser verificada de fato
quando você substitui em ambas as
funções valores iguais. Vamos testar
completando a tabela abaixo.
Os dois primeiros valores são menores
4
que
e os dois últimos são maiores.
5
MATEMÁTICA I
29
FUNÇÃO DO 1º GRAU
x
f(x)
g(x)
Qual é
maior?
23) Para que valores reais de x a função
2 x
f x    é negativa?
3 2
-1
1
3
4
5
1
4
Este mesmo exemplo pode ter
uma solução gráfica.
No plano cartesiano abaixo, você
pode ver os gráficos das duas funções.
24) Para que valores do domínio da
função de
em
definida por
3x  1
a imagem é menor que 4?
f x  
2
4
, as funções
5
são iguais (é o ponto onde elas se
4
cruzam). Para valores menores que , a
5
função f é menor que a função g e isto
pode ser verificado pois à esquerda de
4
x = o gráfico de f está abaixo do gráfico
5
de g. Esta situação se inverte à direito de
4
x= .
5
Note que em x =
CÁSSIO VIDIGAL
30
IFMG – CAMPUS OURO PRETO
c) f(x)  h(x)
25) Dadas as funções f(x) = 2x + 3,
4x  1
hx  
g(x) = 2 – 3x e
2 , definidas em
, para que valores reais de x tem-se:
a) f(x) > g(x)
26)
b) g(x) < h(x)
MATEMÁTICA I
Dados os gráficos das funções f, g e h
definidas em
e considerando cada
quadrinho como uma unidade, determine
os valores de x 
, tais que:
a) f(x) > g(x)
31
FUNÇÃO DO 1º GRAU
b) g(x)  h(x)
27) Dado um número real k, a função
f:

definida por 𝑓(𝑥) = 𝑘 ∙ 𝑥 é
chamada de função linear (pág. 2).
a) Prove que o gráfico da função linear
passa pela origem do sistema de
ordenadas.
c) f(x)  h(x)
d) g(x) > 4
b) Prove que se f é linear então
f(a + b) = f(a) + f(b)  x 
.
e) f(x)  0
CÁSSIO VIDIGAL
32
IFMG – CAMPUS OURO PRETO
28) Uma grandeza y é diretamente
proporcional a uma grandeza x quando y
é uma função linear de x. Se y é
diretamente proporcional a x e quando
x = 4 temos y = 10. Então, para
x = 10, qual é o valor de y?
SISTEMA DE INEQUAÇÕES
Um sistema de inequações é um
conjunto de duas ou mais inequações
consideradas simultaneamente o que
equivale a inequações em x separadas
pelo conectivo e, O conjunto solução do
sistema
de
inequações
é
a
INTERSECÇÃO dos conjuntos-solução
das diversas inequações que a formam.
Ex.1: Resolver o sistema de inequações
3  2 x  1 1
.

3 x  1  5 2
Resolução:
De 1 ,
3  2x  1
 2 x  2
x 1
De 2 ,
3x  1  5
3x  6
x2
Vamos, agora, fazer a interseção entre as
soluções:
Logo, a solução é:
S={x
MATEMÁTICA I
33
| 1  x  2}
FUNÇÃO DO 1º GRAU
conectivo e, aquele mesmo da
intersecção
entre
conjuntos
que
estudamos na primeira apostila.
Ex.2: Resolver o sistema
x 1 x 1
 3  2  4 1

1  x  2  0
2

3
Por isso, para resolver uma
situação com inequações simultâneas,
devemos gerar um sistema de duas (ou
mais) inequações e fazer a intersecção
entre as soluções de cada inequação.
Assim:
De 1 ,
x 1 x 1
2x  1  3x  1

4
4
3
2
6
 2 x  2  3 x  3  24   x  5  24 
  x  29  x  29
 f x   g x 
f  x   g x   hx   
g x   hx 
Indicando por S1 o conjunto
solução da primeira inequação e por S2 o
conjunto solução da segunda inequação,
o conjunto solução das inequações
simultâneas é:
De 2 ,
1
x2
x2
 0  1
3 x2
3
3
 1 x  x  1
S = S 1  S2
Ex.: Resolver 3x  2  x  3  x  4
S={x
| x  -29}

3 x  2   x  3 1


 x  3  x  4 2
INEQUAÇÕES SIMULTÂNEAS
Uma
dupla
desigualdade
f(x) < g(x) < h(x) pode ser decomposta em
duas desigualdades simultâneas, isto é,
equivale a uma sistema de duas
inequações em x separadas pelo
CÁSSIO VIDIGAL
34
De 1 ,
3x  2  x  3
De 2 ,
x 3  x 4
4x  1
1
x
4
 1  2x
1
 x
2
IFMG – CAMPUS OURO PRETO
5 x  1  3 x  2
b) 
6 x  2  8 x  4
A intersecção desses dois conjuntos é
S={x
| 
1
1
x }
2
4
29) Resolver os sistemas a seguir:
3 x  3  0
a) 
 3 x  12  0
MATEMÁTICA I
35
FUNÇÃO DO 1º GRAU
2x  1  2x  1  0
c) 
5 x  2x  2  0
CÁSSIO VIDIGAL
1  32  x   25 x  1
d) 
6 x  3x  1  1  7 x
36
IFMG – CAMPUS OURO PRETO
30) Resolver as inequações em
a) -2 < 3x – 1 < 4
c) -3 < 3x – 2 < x
:
b) -4 < 4 – 2x  3
d) x  1  7  3 x 
MATEMÁTICA I
37
x
1
2
FUNÇÃO DO 1º GRAU
e) 3x + 4 < 5 <6 – 2x
31) Com base nos gráficos das funções f,
g e h definidas em
, determinar os
valores de x 
, tais que:
a) f(x) < g(x)  h(x)
f) 2 – x < 3x + 2 < 4x + 1
CÁSSIO VIDIGAL
38
IFMG – CAMPUS OURO PRETO
b) g(x)  f(x)  h(x)
INEQUAÇÕES-PRODUTO
Sendo f(x) e g(x) duas funções na
variável x, as inequações
f(x)  g(x) > 0
f(x)  g(x) < 0
f(x)  g(x)  0
f(x)  g(x)  0
são denominadas inequações-produto.
Vejamos, por exemplo, como
determinamos o conjunto solução S de
uma inequação do tipo f(x)  g(x) > 0.
De acordo com a regra dos sinais
do produto de números reais, um número
x0
é
solução
da
inequação
f(x)  g(x) > 0 se, e somente se, f(x) e g(x),
não nulos, têm o mesmo sinal.
c) h(x)  f(x) < g(x)
Assim, são possíveis dois casos:
1º: f(x) > 0 e g(x) > 0
Se S1 e S2 são, respectivamente,
os
conjuntos-soluções
dessas
inequações, então S1  S2 é o conjunto
solução do sistema.
2º: f(x) < 0 e g(x) < 0
Se S3 e S4 são, respectivamente,
os
conjuntos-soluções
dessas
inequações, então S3  S4 é o conjunto
solução do sistema.
MATEMÁTICA I
39
FUNÇÃO DO 1º GRAU
f(x) = x + 2
x + 2 = 0  x = -2
Como a função é crescente,
Daí concluímos que o conjuntosolução
da
inequação
produto
f(x)  g(x) > 0 é:
S = (S1  S2 )  (S3  S4 )
Um raciocínio análogo poderia ser
feito para f(x)  g(x) < 0 porém buscando
intervalos onde as funções possuem
sinais diferentes.
Também no caso de f(x)  g(x)  0
ou f(x)  g(x)  0, podemos agir da mesma
forma sendo possível, neste caso, marcar
os pontos que anulam cada função.
Ex.1: Resolver em
x  22x  1  0 .
g x   2 x  1
1
2
Esta função também é crescente, então,
2x  1  0  x 
, a inequação
Resolução
Vamos agora montar um quadro
para o estudo do sinal da inequação
produto:
Como
estamos
procurando
valores para x que tornem o produto
x  22x  1 positivo, então sabemos
que x  2 e 2x  1 devem ter o mesmo
sinal.
A forma mais prática de encontrar
os intervalos onde isto acontece é fazer
um estudo dos sinais de cada parte e
montar num quadro como você verá.
Assim temos a solução:
S={x
CÁSSIO VIDIGAL
40
| x  2 ou x 
1
}
2
IFMG – CAMPUS OURO PRETO
Ex.2:
Resolver em
a inequação
3x  2x  13  x   0
Quando uma inequação-produto
apresenta  ou , devemos lembrar que
as raízes de cada uma das funções que
formam a inequação-produto zeram toda
a inequação e, desta forma, devem fazer
parte da solução.
Resolução:
f x   3 x  2
3x  2  0  x 
2
3
Veja no exemplo.
g x   x  1
x  1  0  x  1
Ex.1: Resolver em
x  22x  1  0 .
h x   3  x
f(x) = x + 2
x+2=0x=2
3x 0 x 3
, a inequação
g x   2 x  1
O próximo passo é montar o
quadro de sinais onde a linha S é a
solução obtida de
f x   g x   hx 
2x  1  0  x 
1
2
Assim temos a solução:
S={x
| x  2 ou x 
1
}
2
E temos a solução:
2
S={x
|  1  x  ou x  3 }
3
_______________________________
MATEMÁTICA I
41
FUNÇÃO DO 1º GRAU
Dentre as inequações-produto,
são importantes as inequações do tipo:
f x n  0
f x n  0
f x n  0
Ex.1:
3x  23  0  3x  2  0  S  x   | x  2 

f x n  0
3
Ex.2:
4x  36  0  4x  3  0  S  x   | x  3 
Para resolver estas inequações,
vamos lembrar duas propriedades das
potências de base real e expoente inteiro:
 “toda potência de base real e
expoente par é um número real
não negativo”, isto é:

Ex.3:
2x  15  0  2x  1  5  S  x   | x   1 

a2n  0,  a  ,  n  N
Ex.4:
x  24  0  S  

Ex.5:
“toda potência de base real e
expoente ímpar conserva o sinal
da base”, ou seja:
2
8  2x 7  0  8  2x  0  S  x   | x  4
Ex.6:
3x  12  0  S  
a2 n1  0  a  0
a2 n1  0  a  0
a2 n1  0  a  0
4
Ex.7:
8  4x 4  0  8  4x  0  S  4
 n N
Assim sendo, temos as seguintes
equivalências:
f x   0
f x   0
f x n  0  
se n é ímpar
se n é par
f x   0 se n é ímpar
x   se n é par
f x n  0  
f x   0 se n é ímpar
x  Df  se n é par
f x n  0  
f x   0
f x   0
f x n  0  
CÁSSIO VIDIGAL
se n é ímpar
se n é par
42
IFMG – CAMPUS OURO PRETO
c) 5x  22  x 4x  3  0
32) Resolver em
seguir:
as inequações a
a) 3x  35x  3  0
d) 3x  2 3x  4x  6  0
b) 4  2x 5  2x   0
MATEMÁTICA I
43
FUNÇÃO DO 1º GRAU
e) 6x  12x  7  0
g) 3  2x 4x  15x  3  0
f) 5  2x  7x  2  0
CÁSSIO VIDIGAL
h) 5  3x 7  2x 1 4x   0
44
IFMG – CAMPUS OURO PRETO
33) Resolver em
seguir:
4
a) x  3  0
e) 3 x  5  0
2
as inequações a
f) 5 x  1  0
3
b) 3 x  8  0
3
g) 4  3 x   0
4
c) 4  5 x   0
6
h) 3 x  8  0
d) 1  7 x   0
5
5
MATEMÁTICA I
45
FUNÇÃO DO 1º GRAU
34) Resolver em
a inequação
5
6
x  3  2x  3  0
(Esta questão está resolvida na seção de
Respostas)
CÁSSIO VIDIGAL
35) Resolver em
as inequações:
4
3
a) 5x  4  7x  2  0
46
IFMG – CAMPUS OURO PRETO
c) x  6  6x  2  4x  5  0
b) 3x  1  2  5x   x  4  0
3
MATEMÁTICA I
5
7
8
47
4
10
FUNÇÃO DO 1º GRAU
d) 5x  1  2x  6  4  6x   0
8
6
INEQUAÇÃO-QUOCIENTE
Sendo f(x) e g(x) duas funções de
variável real x, as inequações do tipo
f x 
0
gx 
f x 
0
gx 
f x 
0
gx 
f x 
0
gx 
são denominadas inequações-quociente.
Considerando que regras de sinais
do produto e do quociente de números
reais são análogas, podemos, então,
construir o quadro-quociente de modo
análogo ao quadro-produto observando o
fato de que o denominador de uma fração
nunca pode ser nulo.
Ex.: Resolver em
a inequação
3x  4
 2.
1 x
Resolução:
Inicialmente devemos transformar a
desigualdade de forma a compará-la a 0
(zero).
______________________
ATIVIDADES COMPLEMENTARES
Pág. 164– Ver R.7
______________________
CÁSSIO VIDIGAL
48
IFMG – CAMPUS OURO PRETO
3x  4
3x  4
2
20
1 x
1 x
3 x  4 21  x 

0
1 x
1 x
3 x  4  2  2x
0
1 x
5x  2
0
1 x
36) Resolver em
2x  1
a)
0
x2
as inequações:
f x   5 x  2
5x  2  0  x  
2
5
g x   1  x
1 x  0  x  1
Fazendo o quadro-quociente para o
estudo dos sinais, temos:
Solução:
S={x
MATEMÁTICA I
| x
2
ou x  1 }
5
49
FUNÇÃO DO 1º GRAU
b)
3x  2
0
3  2x
c)
3  4x
0
8x  1
CÁSSIO VIDIGAL
d)
50
 3  2x
0
3x  1
IFMG – CAMPUS OURO PRETO
37) Resolver em
5x  3
a)
 1
3x  4
MATEMÁTICA I
as inequações:
b)
51
5x  2
2
3x  4
FUNÇÃO DO 1º GRAU
c)
x 1
3
x 1
CÁSSIO VIDIGAL
d)
52
3x  5
1
2x  4
IFMG – CAMPUS OURO PRETO
38) Resolver em
as inequações:
1  2x 3  4 x   0
a)
4  x 
MATEMÁTICA I
b)
53
3 x  1  0
2x  55 x  3
FUNÇÃO DO 1º GRAU
c)
5 x  44 x  1  0
5  4 x 
CÁSSIO VIDIGAL
d)
54
1  2x   0
5  x 3  x 
IFMG – CAMPUS OURO PRETO
39) Resolver em
1
2
a)

x 4 x 3
MATEMÁTICA I
as inequações:
b)
55
1
2

x 1 x  2
FUNÇÃO DO 1º GRAU
c)
x 1 x  3

x2 x4
CÁSSIO VIDIGAL
d)
56
x 5
x 2

3x  2 3x  5
IFMG – CAMPUS OURO PRETO
e)
5x  2 5x  1

4x  1 4x  5
MATEMÁTICA I
f)
57
1
2
3


0
x 1 x  2 x  3
FUNÇÃO DO 1º GRAU
g)
2
1
1


3x  1 x  1 x  1
40) Construa, num mesmo plano
cartesiano, o gráfico das funções abaixo.
f(x) = x
g(x) = x + 3
h(x) = x - 3
______________________
ATIVIDADES COMPLEMENTARES
Pág. 168– Análise de Resolução
______________________
CÁSSIO VIDIGAL
58
IFMG – CAMPUS OURO PRETO
41) Construa, num mesmo plano
cartesiano, o gráfico das funções abaixo.
f(x) = -x
g(x) = -x + 3
h(x) = -x - 3
MATEMÁTICA I
42) Construa, num mesmo plano
cartesiano, o gráfico das funções abaixo.
f(x) = 2x - 4
g(x) = x - 4
h(x) = -x - 4
59
FUNÇÃO DO 1º GRAU
43) Construa o gráfico da função:
 x  2 para x  1
f x   
3 x  6 para x  1
CÁSSIO VIDIGAL
44) Construa o gráfico da função:
2 x  3 para x  2

f x    x  3 para 2  x  4
 x  5 para x  4

60
IFMG – CAMPUS OURO PRETO
RESPOSTAS
4) a)
1)
b)
2)
c)
3)
d)
MATEMÁTICA I
61
FUNÇÃO DO 1º GRAU
e)
5) Resolução:
SOLUÇÃO ANALÍTICA.
Existem diversas formas de
se resolver analiticamente esta
questão como, por exemplo, por
substituição, por adição ou por
comparação. Aqui vou resolver
apenas por adição mas você pode
[e deve] escolher outra forma.
 x  y  3   2

2x  3 y  4
 2 x  2 y  6

2x  3 y  4
x  y  3
f)
5 y  10
x  2  3
y2
x  1
Solução: S = {(-1; 2)}
g)
SOLUÇÃO GEOMÉTRICA
O primeiro passo para
resolver pelo método geométrico é
escrever um sistema equivalente
àquele dado porém isolando y em
ambas as equações.
y  x  3
x  y  3



 2x  4
y
2x  3 y  4

3

Agora vamos construir os gráficos
de cada umas das funções afins e
o ponto de intersecção entre os
dois gráficos será a solução do
sistema.
 2x  4
x x3 y
x
Y
3
h)
0
-4
CÁSSIO VIDIGAL
62
03
3
 4  3 -1
2
-4
 22  4
3
 2 4  4
3
IFMG – CAMPUS OURO PRETO
0
4
8) Resolução
Se estamos procurando uma
equação de reta, então esta
equação assumirá a forma de uma
função afim do tipo y = ax + b.
Desta forma, considerando
que o ponto (1, 2) pertence à reta
de equação y = ax + b, temos a
sentença verdadeira
2=a •1+b a+b=2
Analogamente, para o ponto
(3, -2) obtemos:
-2 = a • 3 + b  3a + b = -2
Resolvendo, agora, o sistema
a  b  2

3a  b  2
encontramos a = -2 e b = 4.
Substituindo a e b em y = ax + b,
encontramos a equação procurada
que, neste caso, é:
y = -2x + 4
Solução: S = {(-1; 2)}
6) a)
b)
S = {(3; 2)}
b)
c)
S = {(-2; 4)}
d)
y = 2x + 1
y=x–5
1  3x
y
2
9) Resolução
A equação procurada é da
forma y = ax + b. Se o coeficiente
angular é 2, então a = 2.
Substituindo x = 1, y = 3 e
a = 2 em y = ax + b, vem:
3=2•1+bb=1
Logo, a equação procurada é
c) S = Ø
Y = 2x + 1
7) a)
b)
MATEMÁTICA I
S = {(3; -1)}
S = {(2; 1)}
63
10)
y = -3x – 2
11)
y
12)
y
x 1

2 2
3
x4
2
FUNÇÃO DO 1º GRAU
13)
14)
y
a)
b)
c)
d)
15)
a)
b)
c)
x
3
3
b)
x 1
y 
3 3
x
y  4
2
2x 1
y

3 3
y = 2x + 3
c)
Crescente:
] - ; -7[, ]-6; -4[ e ]1; [
Decrescente:
]-7; -6[ e ]-4; 1[
Crescente: ] -1; 0[ e ]1; [
Decrescente: ] - ; -1[ e ]0; 1[
Crescente: ] - ; 0[ e ]0;  [
16)
Demonstração
17)
Crescente: a, b, e, f, g.
Decrescente: c, d, h.
18)
k > -5
19)
a)
21)
a)
b)
b)
c)
d)
20)
a)
CÁSSIO VIDIGAL
Crescente para
k–1>0k>1
Constante para
k–1=0k=1
Decrescente para
k–1<0k<1
Cresc.: k > -5
Const.: k = -5
Decresc.: k < -5
Cresc.: k < 4
Const.: k = 4
Decresc.: k > 4
Cresc.: k > 0
Const.: k = 0
Decresc.: k < 0
c)
d)
e)
f(x) < 0 para -1 < x < 0 ou
4<x<7
f(x) = 0 para x = -4 ou x = 1
ou x = 6
f(x) > 0 para -4 < x < 1
f(x) < 0 para x < -4 ou
1 < x < 6 ou x > 6
f(x) = 0 para x = -2 ou x = 0
ou x = 2
f(x) > 0 para x < -2 ou x > 2
f(x) < 0 para -2 < x < 0 ou
0<x<2

y


y


y


y


y


y

y

y
y

3
2
3
 0 para x  
2
3
 0 para x  
2
2
 0 para x 
3
2
 0 para x 
3
2
 0 para x 
3
 0 para x  
 0 para x  4
 0 para x  4
 0 para x  4
y  0 para x  5

y  0 para x  5
y  0 para x  5

y  0 para x  6

y  0 para x  6
y  0 para x  6

f(x) = 0 para x = -1 ou x = 0 ou
x = 4 ou x = 7
f(x) > 0 para x < -1 ou
0 < x < 4 ou x > 7
64
IFMG – CAMPUS OURO PRETO
9

y  0 para x   2

9

y  0 para x  
2

9

y  0 para x   2

f)
2

y  0 para x  3

2

y  0 para x 
3

2

y  0 para x  3

g)
x
24)
x<3
25)
a)
26)
a)
b)
c)
d)
e)
y = 25
29)
a)
S={x
b)
S={x
c)
S={x
d)
S=
a)
S={x
| 
b)
S={x
|
c)
S={x
d)
S=
e)
S={x
f)
S={x
31)
a)
b)
c)
S={x
S={x
S=
|1<x4}
| -3  x  1}
32)
a)
S={x
| x  1 ou x 
b)
S={x
| x
4
3
23)
c)
28)
30)
5
x
4
b)
(Demonstração)
y  0 para x  0

y  0 para x  0
y  0 para x  0

h)
22)
27)
x
1
5
| 2 x 4 }
1
| 3  x  }
2
4
| x }
3
1
5
x }
3
3
1
x4 }
2
1
|   x 1 }
3
1
}
3
| x 1 }
| x
5
ou x  2
2
}
1
2
x
x
c)

x>2
x0
 x 
x < -2
x3
d)
3
ou
4
2
 x  2}
5
S = {x
x  6}
e)
| x
S = { x 
S={x
| 
2
4
ou
x
3
3
| x
7
1
ou x 
2
6
}
MATEMÁTICA I
3
}
5
65
FUNÇÃO DO 1º GRAU
f)
S={x
g)
S = { x 

h)
2
5
x }
7
2
3
| x
ou
5
se x  
é:
S = { x 
|
1
5
ou
x
4
3
Montando o quadro para estudo
de sinais, temos:
7
}
2
a)
S={x
b)
S={x
c)
S=
d)
S={x
e)
S=
f)
S={x
g)
S={ 
h)
S={x
| x 3 }
8
| x }
3
| x
1
}
7
Assim,
S={x
1
| x }
5
35)
4
}
3
| x
Lembrando que potência de
expoente ímpar e base real tem
sinal da base então o sinal de (x –
3)5 é igual ao sinal de x – 3, isto é:
| x
2
}
7
S={x
b)
S={x
| 
S={x
1
x }
2
| x  2 ou
S={x
| x
8
}
3
Solução:
Estudaremos,
separadamente, os sinais das
funções f(x) = (x – 3)5 e
g(x) = (2x + 3)6.
3
| x 3 e x   }
2
a)
c)
34)
3
3
e é nulo se x   , isto
2
2
1
3
x }
4
2
x
33)
| 
d)
36)
a)
b)
1
2
x }
3
5
1
S={x | x  6 ou x 
3
5
ou x   }
4
1
S={x
| x  ou
5
x  3 }
2
3
ou x 
3
2
}
c)
c) S = { x 
S={x
A potência de expoente par
e base real não nula é sempre
positiva, então (2x + 3)6 é positivo
CÁSSIO VIDIGAL
d)
66
1
3
x }
5
4
3
| x   ou
2
| 
1
x }
3
IFMG – CAMPUS OURO PRETO
37)
a)
b)
c)
d)
38)
a)
| x
S={x
}
S={x
4
x }
3
S={x
S={x
| x  10 ou
|  2  x  1}
| 1 x  2}
| 
S={x
S = {x 

c)
d)
a)
b)
c)
d)
e)
f)
MATEMÁTICA I
5
ou
2
3
1
x }
5
3
41)
| x
4
ou
5
1
5
x }
4
4
S={x
x  5}
39)
3
1
 x  ou
4
2
| x
S={x

S={x
|  1  x  0 ou
1
 x  1 ou x  3 }
3
40)
x  4}
b)
g)
7
4
ou x 
8
3
S={x
x > 11}
S={x
x > 2}
S={x
|
1
 x  3 ou
2
| -3 < x < 4 ou
42)
| 0 < x < 1 ou
| -4 < x < -2}
5
S={x | x   ou
3
29
2

x }
24
3
5
9
S={x |  x
4
42
1
ou x  }
4
3
S={x | x  1 ou  x  2
2
ou x  3 }
67
FUNÇÃO DO 1º GRAU
Links para as vídeos-aulas sugeridas
43)
Pág. 07
http://vidigal.ouropreto.ifmg.edu.br/
graficof1g/
Pág. 27
http://vidigal.ouropreto.ifmg.edu.br/
estudosinalf1g
44)
Pág. 42
http://vidigal.ouropreto.ifmg.edu.br/
inequacao-produto/
REFERÊNCIA BIBLIOGRÁFICA
DANTE,
Luiz
Roberto;
Matemática. São Paulo, Ática, 2004
MACHADO, Antônio dos Santos;
Matemática, Temas e Metas. São Paulo,
Atual, 1988
IEZZI,
Gelson
e
outros;
Fundamentos da Matemática Elementar,
Volume 1. São Paulo, Atual, 5ª edição
CÁSSIO VIDIGAL
68
IFMG – CAMPUS OURO PRETO