Ponto, reta e plano no espaço tridimensional, cont.
Matemática para arquitetura
Ton Marar
1. Posições relativas
Posição relativa entre pontos
Dois pontos estão sempre alinhados.
−−−→
Três pontos P1 = (x1 , y1 , z1 ), P2 = (x2 , y2 , z2 ) e P3 = (x3 , y3 , z3 ) estão alinhados se os vetores P1 P2 e
−−−→
P1 P3 forem paralelos. Do contrário, P 1, P 2 e P 3 determinam um triângulo. Assim, P1 , P2 e P3 estão
−−−→ −−−→
alinhados se, e somente se, ||P1 P2 ∧ P1 P3 || = 0.
Posição relativa entre ponto e reta
→
Consideremos um ponto Q = (x1 , y1 , z1 ) e uma reta r : X = P + t−
r , t ∈ R. Se existe
um parâmetro t0
 x = x0 + tr1
−
y = y0 + tr2 ,
para o qual Q = P + t0 →
r , então o ponto Q pertence à reta r. Em outras palavras, se

z = z0 + tr3

 x1 = x0 + t0 r1
y1 = y0 + t0 r2 para algum parâmetro
t ∈ R é a equação paramétrica da reta r, o ponto Q ∈ r ⇐⇒

z1 = z0 + t0 r3
t0 ∈ R.
Posição relativa entre ponto e plano
Consideremos um ponto P = (x0 , y0 , z0 ) e um plano π : ax + by + cz + d = 0.
P ∈ π ⇐⇒ ax0 + by0 + cz0 + d = 0.
Posição relativa entre duas retas
→
→
Sejam r : X = P + λ−
r e s : X = Q + µ−
s duas retas.
→
→
As retas são paralelas se, e somente se, os vetores diretores −
r e−
s são paralelos.
Caso contrário, as retas podem ser concorrentes quando r ∩ s = {ponto} ou reversas quando r ∩ s = ∅.
Exemplos:


 x = 2µ
 x=1+λ
y = µ , µ ∈ R duas retas. Note que os vetores diretores
y = 1 + 2λ , λ ∈ R e s :
1) Sejam r :


z = −λ
z = −2µ
−
→
→
r = (1, 2, −1) e −
s = (2, 1, −2) não são paralelos. Portanto as retas podem ser concorrentes ou reversas.
Verifiquemos se existem um ponto de r e s em comum. Para tanto igualamos as coordenadas dos pontos
das retas: 1 + λ = 2µ, 1 + 2λ = µ e −λ = −2µ.
Da primeira equação λ = −1 + 2µ. Substituindo na segunda obtemos 1 − 2 + 4µ = µ, isto é, µ = 13
e portanto λ = −1
3 . Porém a última equação não se verifica com esses valores. Portanto as retas não
possuem nenhum ponto em comum, logo r e s são reversas.
2) Um par de retas reversas possui uma reta perpendicular a ambas. Para ver isso no caso das retas
r e s do exemplo anterior, considere o plano π que passa pelo ponto (1, 1, 0) da reta r e tem a direção
→
→
→
−
dos vetores −
r e −
η = −
r ∧→
s = (1, 2, −1) ∧ (2, 1, −2) = (−3, 0, −3). Uma equação de π é dada pelo
determinante
¯
¯
¯ x−1 y−1 z ¯
¯
¯
¯ 1
2
−1 ¯¯ = −6(x − 1) + 6(y − 1) + 6z = 0.
¯
¯ −3
0
−3 ¯
A reta s ”fura” o plano π : x − y − z = 0 num ponto, digamos M, e a reta perpendicular procurada é
→
a reta que passa por M e tem a direção do vetor −
η.
Para determinar as coordenadas de M basta substituir as coordenadas dos pontos da reta s na equação
geral de π. Ou seja, 2µ − µ + 2µ = 0, e portanto µ = 0. Logo, Q = (0, 0, 0). Assim a reta procurada tem
equação X = (0, 0, 0) + t(−3, 0, −3); t ∈ R.
1
2
r
P
s
s
M
Em geral, a direção da reta perpendicular às retas reversas r e s é o produto vetorial dos vetores diretores
−
→
→
r ∧−
s . Para determinar a equação da reta perpendicular falta determinar um ponto. Este ponto é obtido
→
→
como interseção da reta s com o plano que tem a direção do vetor −
r ∧−
s e contém a reta r.
Posição relativa entre reta e plano
Sejam r a reta de equação paramétrica

 x = x0 + tr1
y = y0 + tr2 , t ∈ R

z = z0 + tr3
e π o plano de equação geral ax + by + cz + d = 0. Substituindo-se as coordenadas dos pontos da reta r
na equação geral do plano π obtemos a equação a(x0 + tr1 ) + b(y0 + tr2 ) + c(z0 + tr3 ) + d = 0, na variável
t. Tal equação pode ter três tipos de solução, a saber: (i) uma única solução t = t0 , neste caso a reta
”fura” o plano no ponto de coordenadas (x0 + t0 r1 , y0 + t0 r2 , z0 + t0 r3 ), (ii) infinitas soluções, neste caso
a reta r está contida no plano π ou (iii) não existe solução, neste caso a reta é paralela ao plano.
→
Os casos (ii) e (iii) são caracterizados pelo produto escalar do vetor diretor −
r = (r1 , r2 , r3 ) da reta e
−
→
−
→
−
→
o vetor normal η = (a, b, c) do plano se anular, isto é, η · r = 0, enquanto o caso (i) é caracterizado
→
→
pelo oposto, isto é, −
η ·−
r 6= 0.
Posição relativa entre planos
Sejam π1 e π2 dois planos dados pelas equações gerais a1 x + b1 y + c1 z + d1 = 0 e a2 x + b2 y + c2 z + d2 = 0
−
respectivamente. Podemos ter: (i) π1 e π2 paralelos, quando os vetores normais →
η1 = (a1 , b1 , c1 ) e
−
→
−
→
−
→
η2 = (a2 , b2 , c2 ) são paralelos, ou seja, existe um escala α tal que η1 = α η2 . Se além disso, d1 = αd2 então
π1 = π2 .
(ii) Caso contrário π1 e π2 se interceptam numa reta.
→
→
Essa reta tem direção dada pelo produto vetorial −
η1 ∧ −
η2 . Um ponto por onde passa essa reta tem
coordenadas que verificam as duas equações gerais.
Exemplo:
→
Sejam π1 : x − y = 0 e π2 : x − 2y − z − 1 = 0 dois planos. Os vetores normais −
η1 = (1, −1, 0) e
−
→
η2 = (1, −2, −1) não são paralelos. Portanto os planos se interceptam numa reta. Seja r = π1 ∩ π2 . A
→
−
direção de r é dada pelo vetor −
η1 ∧ →
η2 = (1, 1, −1). Os pontos de π1 têm coordenadas x = y. Substituindo
na equação do plano π2 obtemos −y − z − 1 = 0. Portanto z = −y − 1. Assim, um ponto comum
aos dois planos é por exemplo, P = (0, 0, −1). Logo a reta r interseção dos dois planos tem equação
r : X = (0, 0, −1) + t(1, 2, −1), t ∈ R.
Observação: Sejam π1 : a1 x+b1 y+c1 z+d1 = 0, π2 : a2 x+b2 y+c2 z+d2 = 0 e π3 : a3 x+b3 y+c3 z+d3 = 0
três planos distintos. Então três possibilidades se apresentam, a saber, π1 ∩ π2 ∩ π3 = ∅, π1 ∩ π2 ∩ π3 =
{ponto} ou π1 ∩ π2 ∩ π3 = {reta}.
De fato, vamos analisar geometricamente as várias possibilidades:
1) Os três planos π1 , π2 e π3 são paralelos. Neste caso eles não têm ponto em comum. π1 ∩ π2 ∩ π3 = ∅.
2) Apenas dois planos são paralelos. Neste caso, o terceiro plano corta os dois ao longo de retas
(paralelas). π1 ∩ π2 ∩ π3 = ∅.
3) Nenhum par de planos é paralelo. Seja r = π1 ∩ π2 .
3
Se a reta r está contida no terceiro plano π3 então a interseção π1 ∩ π2 ∩ π3 é a reta r. Neste caso,
diz-se que os três planos constituem um feixe de planos.
Se a reta r é paralela ao terceiro plano π3 então π3 intercepta os outros dois planos ao longo de retas
(paralelas) e portanto π1 ∩ π2 ∩ π3 = ∅.
Se a reta r é concorrente com o plano π3 , r ∩ π3 = {P } então a interseção π1 ∩ π2 ∩ π3 é o ponto P.
−
Analiticamente, sejam →
ηi = (ai , bi , ci ), i = 1, 2, 3 vetores normais aos planos πi , i = 1, 2, 3. Se o vetor
−
→
→
η1 ∧ −
η2 for não nulo então π1 ∩ π2
é uma reta e se
−
→
−
→
η1 ∧ →
η2 · −
η3 = 0 então π1 ∩ π2 ∩ π3 = {reta}, caso contrário, um ponto. Ou seja,
(i) Se o produto vetorial de quaisquer dois dos vetores normais for não nulo então
se o produto misto dos vetores normais for nulo a interseção dos três planos é uma reta. Se o produto
misto dos vetores normais for não nulo a interseção dos três planos é um ponto.
(ii) Se o produto vetorial de quaisquer dois dos vetores normais for nulo então a interseção dos três
planos é vazio.
2. Distâncias
Distância entre pontos
Dados dois pontos P1 = (x1 , y1 , z1 ) e P2 = (x2 , y2 , z2 ) a distância entre eles é o número d(P1 , P2 ) =
−−−→
||P1 P2 ||.
Simetria
Dados três pontos alinhados P1 , P2 e P3 dizemos que P3 é o simétrico de P1 em relação a P2 se d(P1 , P2 ) =
d(P2 , P3 ).
Distância entre ponto e reta Dados um ponto P = (x0 , y0 , z0 ) e uma reta r a distância entre P e r é o
−−→
número d(P, r) = ||P Q||, onde o ponto Q é o pé da (única) perpendicular à reta r passando pelo ponto
P.
P
r
Q
A
−
Seja r : X = A + t→
r , t ∈ R uma equação vetorial da reta r. A área do triângulo retângulo AP Q é igual
−→ −→
−→
||AP ∧AQ||
a
. Por outro lado, este triângulo tem base ||AQ|| e altura igual a d(P, r). Logo,
2
−→ −→
−→ d(P, r)
||AP ∧ AQ||
= ||AQ||
2
2
Portanto, d(P, r) =
−→ −→
||AP ∧AQ||
.
−→
||AQ||
−→
→
Finalmente, como A e Q são pontos da reta r então AQ = t0 −
r , para algum t0 ∈ R. Se t0 = 0 então
A = Q e d(P, r) = d(A, P ). Supondo t0 6= 0 temos:
−→ −
−→ −
−→
→
|t0 | ||AP ∧ →
r ||
||AP ∧ →
r ||
||AP ∧ t0 −
r ||
=
=
.
d(P, r) =
−
→
→
||t0 →
r ||
|t0 | ||−
r ||
||−
r ||
Observação:
No plano de coordenadas x e y (ou seja, quando z = 0) a equação da reta r reduz-se

 x = x1 + tr1
y = y1 + tr2 , t ∈ R. E, como vimos (observação 6, página 2), a reta pode ser escrita na forma
a

z=0
r2
ax + by + c = 0 (equação geral) com −a
b = r1 . Em outras palavras, o vetor de componentes (−b, a, 0) é
um vetor diretor da reta r. Assim, aplicando a fórmula acima, a distância de um ponto P = (x0 , y0 , 0) à
reta r é
4
d(P, r) =
||(x0 − x1 ), (y0 − y1 ), 0) ∧ (−b, a, 0)||
|ax0 + by0 − ax1 − by1 |
|ax0 + by0 + c|
p
=
= p
.
2
2
||(−b, a, 0)||
(a + b )
(a2 + b2 )
Simetria
Dados dois pontos P1 e P2 e uma reta r, dizemos que P2 é o simétrico de P1 em relação a r se a reta
determinada pelos pontos P1 e P2 é perpendicular à reta r e d(P1 , r) = d(P2 , r).
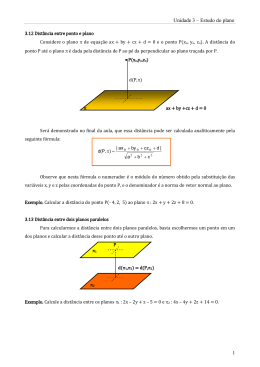
Distância entre ponto e plano
Sejam P = (x0 , y0 , z0 ) um ponto e π : ax + by + cz + d = 0 um plano. A distância de P a π é o número
d(P, π) = d(P, Q), onde Q é o ponto do plano π interseção da reta perpendicular a π passando por P.
Seja A = (x1 , y1 , z1 ) um ponto qualquer do plano π. Então d(P, π) é o módulo da projeção ortogonal do
−→
−
vetor AP sobre o vetor normal →
η = (a, b, c). Calculando-se a projeção ortogonal e tomando-se o módulo
obtemos:
|ax0 + by0 + cz0 + d|
√
d(P, π) =
.
a2 + b2 + c2
Simetria
Dados dois pontos P1 e P2 e um plano π, dizemos que P2 é o simétrico de P1 em relação a π se a reta
determinada pelos pontos P1 e P2 é perpendicular ao plano π e d(P1 , π) = d(P2 , π).
Distância entre duas retas
Sejam r e s duas retas.
Se r e s são paralelas então d(r, s) = d(P, s), onde P ∈ r é um ponto qualquer.
Se r e s são concorrentes então d(r, s) = 0.
Se r e s são reversas então d(r, s) = d(P, Q), sendo P ∈ r e Q ∈ s e o segmento P Q é o segmento
perpendicular comum às retas reversas.
Simetria
Dadas três retas paralelas r, s e t, dizemos que t é a reta simétrica de r em relação a s se as três retas
são coplanares e d(r, s) = d(t, s).
Distância entre uma reta e um plano
Sejam r uma reta e π um plano.
Se r e π são paralelos então d(r, π) = d(P, π), onde P ∈ r é um ponto qualquer.
Se r e π são concorrentes então d(r, π) = 0.
Distância entre dois planos
Sejam π1 e π2 dois planos.
Se π1 e π2 são concorrentes então d(π1 , π2 ) = 0.
Se π1 e π2 são paralelos então d(π1 , π2 ) = d(P, π2 ), onde P ∈ π1 é um ponto qualquer.
Exemplo: A distância entre os planos paralelos π1 : x + y + z + 1 = 0 e π2 : x + y + z − 2 = 0 é a distância
√
√
entre, por exemplo, o ponto P = (0, 0, −1) e o plano π2 . Portanto, d(π1 , π2 ) = d(P, π2 ) = |−1−2|
=
3.
3
Observação: Os planos π1 : ax + by + cz + d1 = 0 e π2 : ax + by + cz + d2 = 0 são paralelos porém
d(π1 , π2 ) 6= |d1 − d2 |.
3. Ângulos
Ângulo entre duas retas
−
→
Sejam r : X = P + λ→
r , λ ∈ R e s : X = Q + µ−
s , µ ∈ R duas retas. O ângulo entre r e s é o ângulo
π
agudo (entre 0 e 2 ) entre as retas. Assim, o ângulo entre as retas r e s será o ângulo entre os vetores
→
→
→
−
diretores −
r e−
s ou entre −
r e −→
s.
Observações:
−
→
−
→
−
−
r
s
1) Seja θ o ângulo entre as retas r e s. Sejam →
u = ||−
e→
v = ||−
vetores diretores unitários de r e s.
→
→
r ||
s ||
→
−
−
→
Então cos(θ) = | u . v |.
5
2) Nos casos extremos, quando o ângulo entre as retas for igual a 0 ou π2 temos denominações especı́ficas
para a posição relativa entre duas retas.
Se o ângulo entre as retas r e s for igual a zero e r ∩ s = ∅ então as retas são ditas paralelas, caso
contrário, se r ∩ s 6= ∅ as retas são coincidentes.
Se o ângulo entre as retas r e s for igual a π2 e r ∩ s = ∅ então as retas (reversas) são ditas ortogonais,
caso contrário, se r ∩ s 6= ∅ as retas são ditas perpendiculares (concorrentes).
Ângulo entre uma reta e um plano
Sejam r uma reta e π um plano. Seja θ o ângulo entre a reta r e uma reta normal ao plano π. O ângulo
entre r e π é igual a π2 − θ.
Observação: Nos casos extremos, quando o ângulo entre uma reta e um plano for igual a 0 ou π2 temos
denominações especı́ficas para a posição relativa entre eles.
Se o ângulo entre a reta r e o plano π for igual a zero e r ∩ π = ∅ então a reta é paralela ao plano π,
caso contrário, se r ∩ π 6= ∅ a reta está contida no plano.
Se o ângulo entre a reta r e o plano π for igual a π2 então r é perpendicular ao plano π, também
chamada reta normal ao plano.
Ângulo entre dois planos
Sejam π1 e π2 dois planos. O ângulo entre π1 e π2 é o ângulo entre retas normais a π1 e π2 .
Observações:
Nos casos extremos, quando o ângulo entre planos for igual a 0 ou π2 temos denominações especı́ficas para
a posição relativa entre dois planos.
Se o ângulo entre os planos π1 e π2 for igual a zero e π1 ∩ π2 = ∅ então os planos são ditos paralelos, caso
contrário, se π1 ∩ π2 6= ∅ os planos são coincidentes.
Se o ângulo entre os planos π1 e π2 for igual a π2 então os planos são ditos perpendiculares.
Exercı́cios
1) Considere as retas r : X = (1, 1, 2)+λ(0, 1, 1); λ ∈ R, s : X = (0, 1, 1)+µ(1, 0, 1); µ ∈ R e t : (x+z −3 =
0) ∩ (x − 2y + z − 1 = 0) (interseção de dois planos.) Mostre que existe um único ponto comum a essas
três retas. Calcule o volume do tetraedro determinado por elas e pelo plano π : x + y − 3z = 0. [15-14]
2) Estude a posição relativa das retas r e s nos seguintes casos:
(a) r : X = (1, −1, 1) + λ(−2, 1, −1); λ ∈ R e s : (y + z = 3) ∩ (x + y − z = 6).
(b) r : (x − y − z = 2) ∩ (x + y − z = 0) e s : (2x − 3y + z − 5 = 0) ∩ (x + y − 2z = 0).
(c) r : (x + 1)/2 = y/3 = (z + 1)/2 e s : (0, 0, 0) + λ(1, 2, 0); λ ∈ R. [16-1]
3) Obtenha uma equação paramétrica da reta perpendicular comum às retas r e s no seguintes casos:
(a) r : X = (2, 0, −1) + λ(1, 1, 1); λ ∈ R e s : x + y − 2 = z = 0.
(b) r : X = (4, 3, 3) + λ(2, −1, 3); λ ∈ R e s : 2 − 2x = y = −z. [17-7]
4) Calcule a distância do ponto de interseção das retas r : X = (1, 3, 4) + λ(1, 2, 3); λ ∈ R e s : X =
(1, 1, 0) + µ(−1, 0, 1); µ ∈ R ao plano determinado pelas retas t : X = (0, 1, 0) + α(0, 6, 1); α ∈ R e
h : x = y − 6z + 8 = 2x − 3. [20-22]
5) Obtenha um vetor diretor da reta que é paralela ao plano x + y + z = 0 e forma ângulo de π/4 com o
plano x − y = 0. [19-20]
6) Obtenha uma equação geral do plano que contém a origem (0, 0, 0) e forma ângulo de π/3 com a reta
r : X = (1, 1, 1) + λ(0, 1, −1); λ ∈ R e com o plano x − y − 4 = 0. [19-30]
7) Uma fonte luminosa situada no ponto F = (0, 0, 1) emite um raio na direção do ponto A = (1, 1, 0) o
qual é refletido por um espelho contido no plano y = 3. Determine o ponto do plano y = 3 onde o raio
incide e o ponto do plano y = 0 atingido pelo raio refletido. [19-12]
8) Obtenha a equação geral do plano que contém a reta r : X = (1, 0, 2)+λ(4, 1, 0); λ ∈ R e é perpendicular
ao plano 3x + y + z = 0. [17-32]