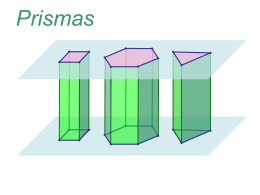
Estudo dos Poliedros
Enchendo a piscina
 A piscina de um clube de minha cidade, vista de cima,
tem formato retangular. O comprimento dela é de 18
m. o fundo é uma rampa reta. Vista lateralmente, ela
tem o formato apresentado na figura.
18 m
x
Outro dia, a piscina estava vazia. O funcionário do
clube abriu o registro e começou a enchê-la. A água
jorrava a uma vazão de 4 litros por segundo.
Enchendo a piscina
 O gráfico a seguir mostra o nível x da água, em
metros, na parte mais funda, em função do volume V
de água despejada, em litros.
Qual é a profundidade
da piscina na parte
mais rasa?
E na parte mais funda?
x (m)
1,8
Qual é a capacidade da
piscina, em litros?
0,8
0
43.200
C
Em quanto tempo a
V ( L) piscina ficará cheia?
Poliedro: uma forma muito especial
 Determinados sólidos tem uma forma muito particular.
Observe os sólidos representados a seguir.
B
C
D
A
E
F
N
M
Q
P
Definição
 Os sólidos apresentados têm algumas característica
comuns:
 São limitados por polígonos;
 Cada lado desses polígonos pertence a exatamente
a dois dos polígonos;
 Dois desses polígonos nunca são coplanares.
Todo sólido que obedece a essas condições é
chamado de poliedro.
Elementos de um poliedro
 Alguns elementos de um poliedro recebem nomes
especiais.
Face de poliedro é cada um dos polígonos que o
delimitam.
Elementos de um poliedro
 Alguns elementos de um poliedro recebem nomes
especiais.
Aresta de poliedro é cada um dos lados das faces. É
cada “quina” do poliedro.
Elementos de um poliedro
 Alguns elementos de um poliedro recebem nomes
especiais.
B
D
A
E
C
F
G
H
Vértice de poliedro é cada um dos vértices das faces.
É cada “ponta” do poliedro.
Elementos de um poliedro
 Alguns elementos de um poliedro recebem nomes
especiais.
O conjunto de todas as faces de um poliedro é
chamado Superfície poliédrica. É a parte externa,
visível. É a “casca” do poliedro.
Poliedro convexo e poliedro côncavo
 Observe os sólidos representados abaixo.
B
C
D
A
E
F
Todo plano que contém qualquer de suas faces deixa
todas as outras num mesmo semi-espaço.
Dizemos, por isso, que eles são poliedros convexos.
Poliedro convexo e poliedro côncavo
 Observe agora o sólido representado abaixo.
N
M
Q
P
O plano que contém a face MNPQ, por exemplo,
deixa as faces do poliedro em semi-espaços
diferentes.
Dizemos, por isso, que ele é um poliedro côncavo.
Classificação dos poliedros
 Os poliedros recebem nomes especiais, de acordo
com o numero n de suas faces (F).
F
Poliedro
F
Poliedro
4
tetraedro
9
eneaedro
5
pentaedro
10
decaedro
6
hexaedro
12
dodecaedro
7
heptaedro
20
icosaedro
8
octaedro
Veja alguns desses poliedros
Hexaedro (P1)
Eneaedro (P3)
Octaedro (P2)
Heptaedro (P4)
Relação de Euler
 Existe uma relação muito importante entre o
número de faces (F), vértices (V) e arestas (A) de
um poliedro convexo.
Poliedro
V
F
A
P1
8
6
12
P2
6
8
12
P3
9
9
16
P4
10
7
15
V+F–A=2
Exemplos
 Um poliedro convexo tem 6 vértices e 12 arestas.
Quantas faces tem?
V+F–A=2
⇒ 6 + F – 12 = 2
⇒ F–6=2
⇒ F=8
Exemplos
 Um poliedro convexo tem 9 faces, sendo 7 quadrangulares e 2 triangulares. Quantos são seus vértices?
Primeiro vamos achar o número de arestas.
9 Faces ⇒
7 quadrang. ⇒ A = 7.4 = 28
2 triang.
⇒
V+F–A=2
2A = 34
⇒ A = 2.3 = 6
⇒
A = 17
⇒ V + 9 – 17 = 2
⇒ V–8=2
⇒
V = 10
Poliedros regulares
 Poliedro regular é todo poliedro em que:
 Todas
as
faces
são
congruentes entre si;
polígonos
regulares,
 De cada vértice, parte o mesmo número de arestas.
Existem apenas cinco classes de poliedros regulares.
O prisma e suas formas
O prisma e suas formas
 Observe os objetos abaixo. Todos têm forma de
poliedro, mas apresentam algumas características
comuns. Eles estão associados a um tipo de
poliedro muito especial: o prisma.
Definição
 Observe a animação.
r


O conjunto de todos esses segmentos é um sólido
poliédrico chamado prisma.
Elementos principais do prisma
F’
E’
A’
D’
O prisma tem dois
tipos de faces
C’
B’
 bases
(polígonos congruentes).
F
 faces laterais
(paralelogramos).
E
A
D
B
C
 Superfície total do prisma é a união da superfície
lateral com as duas bases do prisma.
Elementos principais do prisma
F’
E’
A’
D’
O prisma tem dois
tipos de arestas
C’
B’
 arestas das bases
(AB, A’B’, ..., FA, F’A’).
F
 arestas laterais
(AA’, BB’, CC’, ... ,FF’ ).
E
A
D
B
C
Elementos principais do prisma
F’
E’
A’
C’
B’
D’
h
F
E
A
D
B
C
 A distância h entre as duas bases do prisma é a
altura do prima.
Nomenclatura dos prismas
 Um prisma é classificado pelo tipo de polígono que
constitui suas bases.
Polígonos das bases
Prisma
triângulo
P. triangular
quadrilátero
P. quadrangular
pentágono
P. pentagonal
hexágono
P. hexagonal
Veja alguns desses prismas
Prisma triangular
Prisma Pentagonal
Classificação dos prismas
 Um prisma pode ser classificado, também, pela
posição das arestas laterais em relação ao plano da
base.
Dizemos que ele é:
 prisma reto, se as arestas laterais são perpendiculares aos planos das bases;
 prisma oblíquo, se as arestas laterais são oblíquas
aos planos das bases.
Nos prismas retos, as arestas laterais são alturas
e as faces laterais são retângulos.
Classificação dos prismas
h
h
Prisma triangular
reto
Prisma Pentagonal
oblíquo
Prisma regular
 Todo prisma reto cujas bases são
regulares é chamado de prisma regular.
polígonos
B
A
C
O prisma é reto e
ABC é triângulo eqüilátero
⇒
⇒
Prisma triangular regular
O prisma é reto e a
Base é hexágono regular
Prisma hexagonal regular
Prisma quadrangulares
Prismas quadrangulares
 Todo prisma cujas bases são paralelogramos é
chamado paralelepípedo.
Paralelepípedo
Prismas quadrangulares
 Se as bases de um paralelepípedo reto são
retângulos, ele é chamado paralelepípedo retoretângulo ou paralelepípedo retângulo.
Paralelepípedo retângulo
ou ortoedro
Prismas quadrangulares
 Se todas as arestas de um paralelepípedo
retângulo são congruentes entre si, ele é chamado
cubo ou hexaedro regular.
Cubo ou hexaedro regular
Estudo do cubo
Estudo do cubo
 O cubo é o mais simples dos prismas. Ele é um
prisma quadrangular regular, cujas faces são
quadrados congruentes. Por isso qualquer de suas
faces pode ser considerada como base.
a → medida de cada uma
das arestas
a
a
a
Diagonais no cubo
 Num cubo, distinguimos dos tipos de diagonais.
a → medida de cada uma
das arestas
D
d → diagonal da face
a
d
a
a
D → diagonal do cubo
Diagonais no cubo
 Obtendo os valores d e D em função da medida a
da aresta.
d2 = a 2 + a 2
D
⇒ d = 2a2
a
a
d
a
⇒ d = a√2
a
Diagonais no cubo
 Obtendo os valores d e D em função da medida a
da aresta.
D 2 = a 2 + d2
D
a
⇒ D = a2 + 2a2
a
a
d
a
⇒ D = 3a2
⇒ D = a√3
Área da superfície total do cubo
 Planificando a superfície total de um cubo de
aresta a, obtemos a figura.
a
a
a
a
a
a
a
AT = 6a2
Exemplo
 A área da superfície total de um cubo é 54 cm2. Obter
a medida da diagonal da face e da diagonal do cubo?
AT = 6a2
⇒ 6a2 = 54
d = a√2
⇒ d = 3√2
D = a√3
⇒ D = 3√3
⇒ a2 = 9
⇒ a=3
O cubo como unidade de volume
 Se considerarmos a medida da aresta de um cubo
como unidade de medida de comprimento, a
medida do volume desse cubo é a unidade de
volume.
1u
V = 1 u3
1u
1u
1u
Definida a unidade de comprimento, a unidade de
volume fica automaticamente definida.
O cubo como unidade de volume
 Se considerarmos a medida da aresta de um cubo
como unidade de medida de comprimento, a
medida do volume desse cubo é a unidade de
volume.
1u
V = 1 u3
1u
1u
1u
 Se a unidade de comprimento é 1 m, a unidade de
volume é 1 m3.
 Se a unidade de comprimento é 1 dm, a unidade
de volume é 1 dm3.
Volume
 O volume de um sólido qualquer, numa certa
unidade, é um número que indica quantas vezes o
cubo de volume unitário “cabe” naquele sólido.
 Considerando o cubo da primeira figura como
unidade de medida. Seu volume é 1 u3. qual o
volume dos sólidos abaixo?
V = 1 u3
V = 9 u3
V = 11 u3
Volume do cubo
 Analise as três figuras a seguir.
a=1u
V = 1 u3
a=2u
V = 23 = 8 u3
a=3u
V = 33 = 27 u3
De uma maneira geral, o volume de um cubo cuja
aresta mede a é
V = a3
Exemplo
 Uma diagonal de um cubo mede 6 m. Calcular a área
da superfície total e o volume desse cubo?
D = a√3
⇒ a√3 = 6 ⇒ a =
6
√3
⇒ a = 2√3 m
AT = 6a2
⇒ AT = 6.(2√3)2
⇒ AT = 72 m2
V = a3
⇒ V = (2√3)3
⇒ V = 24√3 m3
Estudo do Paralelepípedo
retângulo
Estudo do paralelepípedo retângulo
 O
paralelepípedo
retângulo
é
um
prisma
quadrangular. Suas faces são duas a duas
congruentes.
a, b e c → As dimensões
do paralelepípedo.
b
a
c
 Suas doze arestas são quatro a quatro congruentes. As medidas dessas arestas são as dimensões
do paralelepípedo.
Diagonal do paralelepípedo
 Diagonal de um paralelepípedo é todo segmento
cujos extremos são dois vértices não-pertencentes
a uma mesma face.
D
d
c
b
a
d → diagonal da face inferior
D → diagonal do paralelepípedo
Cálculo da diagonal do paralelepípedo
 Obtendo o valor de D em função das dimensões a,
b e c do paralelepípedo.
D
c
b
d
a
d2 = a 2 + b2
e
D2 = a2 + b2 + c2
D2 = d2 + c2
⇒ D = √a2 + b2 + c2
Exemplo
 O comprimento e a largura de um paralelepípedo
medem 12 cm e 4 cm. Uma de suas diagonais mede
13. Obter a medida de sua altura?
D = √a2 + b2 + c2
⇒ 13 = √122 + 42 + c2
⇒ 169 = 144 + 16 + c2
⇒
c2 = 9
⇒
c=3
⇒
c2 = 169 – 160
Área da superfície total do paralelepípedo
 Planificando
a
superfície
total
de
um
paralelepípedo de dimensões a, b e c obtemos a
figura.
a
b
c
b
a
c
AT = 2ab + 2ac + 2bc
AT = 2(ab + ac + bc)
bc
ab
ac
ab
ac
bc
Exemplo
 A área da superfície total de um paralelepípedo é 248
cm2. suas dimensões são proporcionais a 2, 3 e 5.
Calcular a medida da diagonal do paralelepípedo?
As dimensões a, b e c são proporcionais a 2, 3 e 5 indica
que a = 2k, b = 3k e c = 5k.
AT = 248
⇒
2(ab + ac + bc) = 248
⇒
ab + ac + bc = 124
⇒
2k.3k + 2k.5k + 3k.5k = 124
⇒
6k2 + 10k2 + 15k2 = 124
⇒
k2 = 4
⇒
k=2
⇒
:(2)
31k2 = 124
Exemplo
 A área da superfície total de um paralelepípedo é 248
cm2. suas dimensões são proporcionais a 2, 3 e 5.
Calcular a medida da diagonal do paralelepípedo?
Logo a = 4, b = 6 e c = 10.
D = √42 + 62 + 102
D = √16 + 36 + 100
D = √152
D = 2√38
Volume do paralelepípedo retângulo
 Analise as duas figuras a seguir.
4u
cubo unitário
V = 1 u3
3u
5u
V = 5.3.4 = 60 u3
De modo geral, o volume de um paralelepípedo de
dimensões a, b e c é dado por
V = a.b.c
Observação
 Podemos
interpretar
o
volume
de
um
paralelepípedo retângulo de outra forma. Veja a
figura a seguir.
c
A = ab
a
b
V = abc = (ab)c = (área da base) . (altura relativa)
V = AB.h
Exemplos
 Uma caixa d’água tem forma de paralelepípedo
retângulo. Suas dimensões internas são 1,2 m, 2,5 m
e 0,8 m. Obter sua capacidade, em litros?
A capacidade de uma caixa é o volume de água que
cabe nela.
V = abc = 1,2 . 2,5 . 0,8 = 2,4 m3
Sabemos que 1 m3 = 1 000 dm3 e que 1 L = 1 dm3.
V = 2 400 dm3 = 2 400 L
Exemplos
 Uma das dimensões de um paralelepípedo é
aumentada em 20%; outra, aumentada em 30%; a
terceira em 10%. O que ocorre com o volume do
paralelepípedo?
Suponhamos que as dimensões sejam x, y e z. Então, o
volume original é V = xyz.
Se x aumenta 20%, a nova dimensão passa para 1,2 x.
Se y aumenta 30%, a nova dimensão passa para 1,3 y.
Se z aumenta 10%, a nova dimensão passa para 1,1 z.
V’ = 1,2x . 1,3 y . 1,1 z = 1,404.xyz = 1,404.V
Concluímos que o volume aumenta 40,4%.
Estudo geral do prisma
Estudo geral do prisma
 Vamos aprender a calcular áreas e volumes em
prismas quaisquer. Em geral. Vamos considerar
prismas retos em que
 As arestas laterais são alturas;
 As faces laterais são retângulos;
B
A
C
Áreas no prisma
 No prisma as áreas.
 Área Lateral (AL) – Soma das áreas dos retângulos;
 Área da base (AB) – Área do polígono da base;
 Área total (AT) – Soma da área lateral com as bases
AT = AL + 2AB
Exemplo
 A figura a seguir mostra um prisma triangular reto,
com as dimensões indicadas. Calcular a área lateral e
a área total desse prisma.
AL = 3.6 + 4.6 + 5.6
AL = 18 + 24 + 30 = 72
6
AB = (3.4)/2 = 6
4
3
5
AT = AL + 2.AB
AT = 72 + 2.6 = 84
Exemplo
 Num prisma hexagonal regular, a altura mede 6 m e a
área de cada base é 24√3 m2. Achar sua área lateral.
A = 24√3
⇒
⇒
x2 = 16 ⇒
3x2√3
= 24√3
2
x=4
6
x
Af = b.h
⇒ Af = 4.6 = 24
AL = 6.Af
⇒ AL = 6.24 = 144 m2
Princípio de Cavalieri
Princípio de Cavalieri
 Bonaventura Cavalieri nasceu na Itália, no final do
século XVI. Discípulo de Galileu, ele deixou
contribuições importantes nas áreas de óptica e
geometria.
Princípio de Cavalieri
 Dados dois ou mais sólidos apoiados em um
mesmo plano , se
 Todos têm a mesma altura;
 Todo plano  paralelo a  e que corte os sólidos
determina, em todos eles, seções planas de
mesma área;
Então os sólidos têm o mesmo volume.
Princípio de Cavalieri
 A figura abaixo ilustra o princípio de Cavalieri.
Volume do prisma
 Vamos deduzir uma fórmula para o cálculo do
volume do prisma. Para isso, vamos aplicar o
princípio de Cavalieri.
V = AB.h
Exemplos
 As bases de um prisma oblíquo são retângulos cujos
lados medem 5 cm e 4 cm. Suas arestas laterais
medem 6 cm e formam, com o plano da base, ângulo
de 60º. Achar o volume do prisma.
5
h
4
60º
6
Exemplos
 O volume de um prisma hexagonal regular é igual a
486 cm3, e sua altura é igual ao apótema da base.
Calcular sua área total.
h
L